Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Исследование статистических свойств алгоритмов минимизации недетерминированных конечных автоматов с использованием программы ReFaM
Аннотация:В статье рассматриваются вопросы минимизации недетерминированных конечных автоматов с использованием программы ReFaM. В данном экспериментальном программном продукте с открытым исходным кодом с использованием технологий параллельного программирования OpenMP и MPI реализованы несколько точных и приближен- ных алгоритмов вершинной минимизации, в частности классический алгоритм Камеды–Вейнера и эвристические алгоритмы на его основе. Как правило, из-за вычислительной сложности алгоритмы минимизации недетерминированных конечных автоматов редко реализуются в программных средствах для работы с конечными автоматами и родственными структурами, поэтому данная программа может использоваться как в исследовательских, так и в учебных целях. Одной из ее отличительных особенностей является детальное описание процесса минимизации и сбор статистики на каждом его шаге. В данной работе приводятся описание основных возможностей программы и некоторые экспериментальные результаты.
Abstract:In the present paper we consider the minimization of nondeterminisitc finite automata using ReFaM. This experimental open source software tool provides several exact and approximate state minimization algorithms, such as classical Kameda–Weiner algorithm and some heuristic algorithms based on it, which are implemented using OpenMP and MPI parallel programming techniques. Usually software products that deal with finite automata and related structures do not provide algorithms for nondeterministic finite automata minimization due to their computational complexity therefore the considered program can be used for research and educational purposes. One of the distinguishing features of this software is that it explains the minimization process in details and collects statistics of all minimization steps. The description of the program features as well as some experimental results is provided.
| Авторы: Цыганов А.В. (andrew.tsyganov@gmail.com) - Ульяновский государственный педагогический университет им. И.Н. Ульянова (профессор), Ульяновск, Россия, кандидат физико-математических наук, Винокуров С.Д. (PhoenixDragonViSta@yandex.ru) - Ульяновский государственный педагогический университет им. И.Н. Ульянова, г. Ульяновск (студент), Ульяновск, Россия, Ведин А.А. (alexlumen@rambler.ru) - Ульяновский государственный педагогический университет им. И.Н. Ульянова, г. Ульяновск (студент), Ведин, Россия | |
| Ключевые слова: mpi., openmp, параллельные вычисления, эвристические алгоритмы, вершинная минимизация, недетерминированные автоматы |
|
| Keywords: mpi, OpenMP, parallel computing, heuristic algorithms, state minimization, nondeterministic finite automata |
|
| Количество просмотров: 11262 |
Версия для печати Выпуск в формате PDF (9.63Мб) Скачать обложку в формате PDF (1.26Мб) |
Недетерминированным конечным автоматом (НКА) называется пятерка A=(Q, S, d, I, F), где Q – конечное множество состояний (вершин автомата); S – конечный алфавит; d:Q´S®2Q – функция переходов; I и F – соответственно множества начальных и конечных состояний. НКА называется детерминированным (ДКА) тогда и только тогда, когда ïIï=1 и "qÎQ, "aÎS:ïd(q, a)ï=1 (иногда ïd(q, a)ï£1). Конечные автоматы (КА) широко применяются в разных областях, в частности в теории формальных языков, где они наряду с другими структурами, например регулярными выражениями (РВ), используются для описания языков [1]. В теории конечных автоматов одной из важнейших является задача вершинной минимизации, которая формулируется следующим образом: для данного автомата Из-за малой практической применимости алгоритмы вершинной минимизации НКА (особенно их точные версии) обычно не реализуются в большинстве программ для работы с конечными автоматами и родственными структурами. Рассмотрим некоторые возможности нового экспериментального программного средства ReFaM (Rational Expressions and Finite Automata Minimization). Основными отличиями данной программы от других программ для работы с КА являются реализация нескольких точных и приближенных алгоритмов минимизации НКА и возможность получения подробного отчета и статистики о каждом шаге работы алгоритма. Все это делает возможным применение рассматриваемой программы как в исследовательских, так и в учебных целях. Основные сведения о программе ReFaM Настоящая программа является проектом с открытым исходным кодом, написанным на языке C++. Данный проект – это часть библиотеки параллельных метаэвристических алгоритмов HeO [3]. Для описания КА в программе ReFaM используется xml-формат. Приведем пример xml-описания НКА (на рисунке соответствующий автомат представлен в виде графа): Каждому символу и состоянию в автомате присваивается уникальный номер (id). При описании автоматов узлы и , описывающие метки символов и состояний, могут быть опущены пользователем. В этом случае данные метки генерируются автоматически. В автоматах допускается наличие пустых e-переходов. Список команд ReFaM с описанием их аргументов приведен в таблице 1. Большинство команд ReFaM имеют вид command in_dir out_dir. Каждая такая команда сканирует все xml-файлы в каталоге in_dir и, если в них содержатся описания автомата или регулярного выражения, обрабатывает их содержимое, а результаты помещает в каталог out_dir. Назначение многих команд понятно из их названия. Остановимся подробнее на некоторых командах. Команда canonize строит для данного автомата минимальный детерминированный (канонический) автомат. Команда re2fa формирует по данному регулярному выражению конечный автомат (с e-переходами), используя теорему Клини. Команда export позволяет конвертировать xml-представление автоматов в другие форматы. Команда generate может использоваться для случайной генерации автоматов. Как правило, подобные команды имеются и в других программах для работы с КА.
Automaton("epsilon", 3, 4, [[,[2],], [[2],[2],[1,3]], [[2],,], [[3],,]], [1], [2,3]), а описание таблицы переходов в формате LaTeX будет выглядеть так: \documentclass[12pt]{article} \usepackage[cp1251]{inputenc} \usepackage{amssymb} \begin{document}
Automaton example (symbols: 3, states: 3, transitions: 7, type: epsilon) \begin{tabular}{lr||c|c|c|c} & & $a$ & $b$ & $c$ & $\epsilon$ \\ \hline \hline $ ightarrow$ & $1$ & $\varnothing$ & $\{2\}$ & $\{2\}$ & $\{3\}$ \\ \hline $\leftarrow$ & $2$ & $\{2\}$ & $\{2\}$ & $\varnothing$ & $\varnothing$ \\ \hline $\leftarrow$ & $3$ & $\varnothing$ & $\{1,3\}$ & $\varnothing$ & $\varnothing$ \\ \end{tabular} \end{document} С помощью команд build_ba и build_com могут быть построены соответственно базисный и полный (COM) автоматы для данного КА или РВ. Оба автомата являются инвариантами для данного регулярного языка, а их определение и алгоритмы построения можно найти, например, в [1]. Заметим, что в известных программах для работы с КА возможность построения данных автоматов отсутствует, кроме того, оба автомата могут использоваться для минимизации НКА по различным критериям. Вершинная минимизация НКА осуществляется с помощью двух команд – min_kw и min_com. В настоящее время в программе ReFaM реализованы точные и приближенные алгоритмы минимизации, основанные на классическом алгоритме Камеды–Вейнера [4] и алгоритме, использующем COM-автомат [1, 5]. В обоих алгоритмах используются двоичные матрицы соответствия состояний (RAM и таблица # соответственно) и минимальные автоматы строятся на основе покрытий данных матриц гридами (подмножествами строк и столбцов). Второй метод идеологически ближе к методу минимизации на основе так называемого уиверсального автомата [6]. Кроме входного и выходного каталогов, в этих командах дополнительно могут указываться конфигурационный файл config.xml с настройками алгоритмов минимизации и начальное значение генератора случайных чисел seed для эвристических версий алгоритмов. В числе отличительных особенностей ReFaM – распараллеливание наиболее трудоемких частей алгоритмов с использованием технологий параллельного программирования OpenMP и MPI и возможность получения подробного отчета и статистики о каждом шаге процесса минимизации. Например, для точного алгоритма Камеды–Вейнера в отчете показываются следующие объекты: исходный автомат A, автоматы det(A) – соответствующий ДКА, rev(A) – зеркальный автомат для A, det(rev(A)) – детерминированный зеркальный автомат для A, min(det(A)) – канонический автомат для A, min(det(rev(A))) – зеркальный канонический автомат для A, а также матрица RAM автомата A и гриды матрицы RAM.
Численные эксперименты Как уже было отмечено, задача вершинной минимизации НКА является вычислительно трудной. Поскольку в точных алгоритмах вершинной минимизации используется полный перебор, то из-за сложности возникающих в процессе минимизации объектов (размеров канонических автоматов, количества гридов и т.п.) данный этап может оказаться очень длительным даже для сравнительно небольших автоматов. Очень интересной задачей является практическое изучение статистических свойств объектов, возникающих в процессе минимизации, в зависимости от характера входных данных. Для решения данной задачи может использоваться программа ReFaM. В командах min_kw и min_com предусмотрена возможность, позволяющая с помощью соответствующей опции в конфигурационном файле построить все необходимые для минимизации объекты, не запуская сам процесс поиска. Рассмотрим результат обработки трех случайных выборок из ста попарно независимых НКА без недостижимых и бесполезных состояний со следующими параметрами: число состояний ïQï=10, число начальных состояний ïIï=1, число конечных состояний ïFï=2, размер алфавита ïSï=2, плотность переходов Для каждой выборки оценивались число состояний в автоматах det(A) и det(rev(A)), число непустых состояний в канонических автоматах (число строк и столбцов RAM), размер, плотность единиц и число гридов в RAM. Результаты исследования представлены в таблице 2 (m – среднее значение, s – среднеквадратическое отклонение). Из приведенных данных видно, что для рассматриваемых выборок с увеличением плотности переходов средняя сложность рассматриваемых объектов уменьшается. В заключение следует отметить, что в работе были рассмотрены некоторые возможности программы ReFaM, предназначенной для минимизации НКА. Отличительными особенностями программы являются возможность получения подробных отчетов о процессе минимизации и сбор обширной статистики, что делает возможным применение данной программы как в исследовательских, так и в учебных целях. В настоящее время ведется работа по добавлению в программу новых точных и приближенных алгоритмов минимизации, а также алгоритмов вершинной минимизации. Литература 1. Мельников Б.Ф. Недетерминированные конечные автоматы. Тольятти: Изд-во ТГУ, 2009. 160 с. 2. Jiang T., Ravikumar B. Minimal NFA problems are hard. SIAM J. Comput. 1993. December. Vol. 22, pp. 1117–1141. 3. Цыганов А.В., Булычов О.И. HeO: библиотека метаэвристик для задач дискретной оптимизации // Программные продукты и системы. 2009. № 4. С. 148–151. 4. Kameda T., Weiner P. On the State Minimization of Nondeterministic Finite Automata. IEEE Transactions on Computers. 1970. Vol. 19, pp. 617–627. 5. Melnikov B. A new algorithm of the state-minimization for the nondeterministic finite automata. Journal of Applied Mathematics and Computing. 1999. Vol. 6, pp. 277–290. 6. Polak L. Minimalizations of NFA using the universal automaton // Int. J. Found. Comput. Sci. 2005. Vol. 16, no. 5, pp. 999–1010. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3327 |
Версия для печати Выпуск в формате PDF (9.63Мб) Скачать обложку в формате PDF (1.26Мб) |
| Статья опубликована в выпуске журнала № 4 за 2012 год. [ на стр. 137-141 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Генетический алгоритм для задачи вершинной минимизации недетерминированных конечных автоматов
- HeО: библиотека метаэвристик для задач дискретной оптимизации
- Метод деформации функционально заданных объектов с применением графических процессоров
- Оценки времени в модели параллельного выполнения программ
- Система моделирования масс-спектрометра на основе параллельного кода частиц в ячейке
Назад, к списку статей



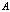 найти эквивалентный ему автомат (то есть автомат, задающий тот же язык), который имел бы минимально возможное число состояний. Как показано в [2], для НКА задача вершинной минимизации является вычислительно трудной (PSPACE-полной), в то время как для ДКА соответствующая задача имеет сложность O(n×log(n)), где n – число состояний в автомате.
найти эквивалентный ему автомат (то есть автомат, задающий тот же язык), который имел бы минимально возможное число состояний. Как показано в [2], для НКА задача вершинной минимизации является вычислительно трудной (PSPACE-полной), в то время как для ДКА соответствующая задача имеет сложность O(n×log(n)), где n – число состояний в автомате. Команда export может использоваться для автоматического перевода xml-представления автоматов в иные форматы: GAP (для использования в пакете Automata программы GAP), Graphviz (для построения графов автоматов в программе Graphviz), а также для получения таблиц переходов в текстовом формате и в формате LaTeX. Например, в результате экспорта xml-описания НКА в формат GAP получается следующий результат:
Команда export может использоваться для автоматического перевода xml-представления автоматов в иные форматы: GAP (для использования в пакете Automata программы GAP), Graphviz (для построения графов автоматов в программе Graphviz), а также для получения таблиц переходов в текстовом формате и в формате LaTeX. Например, в результате экспорта xml-описания НКА в формат GAP получается следующий результат:![Подпись: Таблица 1
Список доступных команд
Команда Аргументы Вход Выход
build_ba in_dir out_dir НКА, РВ НКА
build_com in_dir out_dir НКА, РВ НКА
canonize in_dir out_dir НКА, РВ минДКА
codeterminize in_dir out_dir НКА, РВ ДКА
determinize in_dir out_dir НКА, РВ ДКА
equivalent in_file1.xml in_file2.xml НКА, РВ true/false
export in_dir out_dir НКА TXT, GAP, LaTeX, Graphviz
generate out_dir [options.xml] – ДКА, НКА
isomorphic in_file1.xml in_file2.xml ДКА true/false
min_com in_dir out_dir [options.xml [seed]] НКА, РВ минНКА
min_kw in_dir out_dir [options.xml [seed]] НКА, РВ минНКА
re2fa in_dir out_dir РВ e-НКА
reverse in_dir out_dir НКА НКА
Таблица 2
Результаты минимизации
Параметры D=0,2 D=0,3 D=0,4
min max m s min max m s min max m s
Число состояний в det(A) 7 51 27,46 9,43 4 28 14,37 4,53 3 17 8,88 2,46
состояний в det(rev(A)) 8 44 20,48 7,54 5 15 8,94 2,20 4 9 6,06 1,06
строк в RAM, m 1 29 7,91 4,78 1 9 4,50 1,27 1 6 4,10 0,97
столбцов в RAM, n 1 27 8,09 5,00 1 12 4,66 1,52 1 7 4,19 1,06
Размер RAM (m´n) 1 754 87,03 122,12 1 108 22,78 14,37 1 42 18,16 7,82
Плотность единиц в RAM 0,58 1,00 0,74 0,06 0,60 1,00 0,71 0,06 0,60 1,00 0,73 0,06
Число гридов 1 453 41,30 68,49 1 29 7,23 4,20 1 15 6,41 2,95](uploaded/image/2012-4/image418.gif) Кроме того, для данного алгоритма собирается определенная статистика: размеры всех автоматов, число строк, столбцов, единиц и гридов в матрице RAM, плотность единиц в матрице RAM и др., а также замеряется время выполнения каждого шага алгоритма. В конце работы данные результаты статистически обрабатываются: вычисляются минимальные, максимальные и средние значения, а также среднеквадратическое отклонение. При этом имеется возможность задавать подробность отчета с помощью уровней от 0 (только статистика) до 3 (самый подробный отчет). Аналогичным образом документируется минимизация на основе COM-автомата.
Кроме того, для данного алгоритма собирается определенная статистика: размеры всех автоматов, число строк, столбцов, единиц и гридов в матрице RAM, плотность единиц в матрице RAM и др., а также замеряется время выполнения каждого шага алгоритма. В конце работы данные результаты статистически обрабатываются: вычисляются минимальные, максимальные и средние значения, а также среднеквадратическое отклонение. При этом имеется возможность задавать подробность отчета с помощью уровней от 0 (только статистика) до 3 (самый подробный отчет). Аналогичным образом документируется минимизация на основе COM-автомата. 0,2; 0,3; 0,4, где T – число переходов в автомате (40, 60 и 80 соответственно).
0,2; 0,3; 0,4, где T – число переходов в автомате (40, 60 и 80 соответственно).