Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная конвейеризация циклов для ускорителя плавающей арифметики в составе процессора Комдив128-РИО
Аннотация:Представлен метод программной конвейеризации циклов для специализированного ускорителя в составе процессора Комдив128-РИО архитектуры MIPS. Программирование ускорителя производится только на языке ассемблера, поскольку создание компиляторов с языков высокого уровня для него невозможно из-за ряда архитектурных особенностей. Ручная разработка эффективных вычислительных циклов для ускорителя является сложной задачей, так как программист должен учитывать множество факторов, таких как отсутствие аппаратных задержек по неготовности данных, сложная структура регистрового файла, отсутствие ветвлений и ограниченный аппаратный стек. Целью работы является разработка автоматических средств программной конвейеризации циклов для специализированного ускорителя. Это позволяет программисту писать достаточно простые внутренние циклы, которые правильно реализуют вычисления, но могут быть неоптимальными. Затем исходный цикл трансформируется в конвейеризованный, на нем достигается максимальная или близкая к максимальной эффективность выполнения заданных программистом вычислений. Использование точного подхода, основанного на применении методов целочисленного линейного программирования, позволяет обеспечить оптимальную производительность кода. Основное внимание в статье уделено особенностям формулировки задачи целочисленного линейного программирования, связанным со спецификой архитектуры ускорителя. Рассмотрены вопросы точного подсчета числа требуемых регистров, а также проблема понижения кратности развертки конвейеризованных циклов.
Abstract:The paper presents a method of software pipelining for a specialized floating point accelerator in the Komdiv128-RIO processor with MIPS architecture. Programs for the accelerator may be developed in Assember only. Implementation of a high level languages compiler is impossible due to architectural peculiarities of the accelerator. Manual writing of efficient computational loops for the accelerator is complicated. A programmer should keep in mind miltiple factors, such as lack of hardware delays on unready input data and complicated structure of the register file. The purpose of the work is to develop an instrument for automated software pipelining of loops for the specialized accelerator. A programmer may write quite simple internal loops which implement the calculations correctly but probably inefficiently. The loop is then transforming to a pipelined one with maximal calculating efficiency or close to the maximal one. Use of a precise approach based on integer linear programming (ILP) methods allows achieving the optimal efficiency of a code. The article is focused on specific points of the ILP task formulation connected with peculiarities of the accelerator architecture. The authors discuss the issues of exact calculation of the number of required registers as well as a problem of reducing the unroll factor of pipelined loops.
| Авторы: Вьюкова Н.И. (niva@niisi.msk.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, Галатенко В.А. (galat@niisi.msk.ru) - НИИСИ РАН, г. Москва (зав. сектором автоматизации программирования), г. Москва, Россия, кандидат физико-математических наук, Самборский С.В. (sambor@niisi.msk.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия | |
| Ключевые слова: предикатное выполнен, архитектура сверхдлинного командного слова (vliw), ускоритель арифметических операций с плавающей запятой, целочисленное линейное программирование (цлп), планирование по модулю, программная конвейеризация циклов, оптимизация программ |
|
| Keywords: predicated execution, Very Large Instruction Word (VLIW), floating point accelerator, integer linear programming (ILP), modulo scheduling, software pipelining, program optimization |
|
| Количество просмотров: 11467 |
Версия для печати Выпуск в формате PDF (7.95Мб) Скачать обложку в формате PDF (1.45Мб) |
В НИИСИ РАН разработан процессор К128-РИО, в состав которого включен ускоритель плавающей арифметики – специализированный сопроцессор CP2, ориентированный на выполнение арифметических операций над комплексными числами или векторами длины 2, элементы которых являются значениями одинарной точности с плавающей запятой. Сопроцессор обладает собственной системой команд и накристальной программной памятью. Сопроцессор имеет параллелизм как на уровне команд, так и на уровне данных, что обеспечивает высокий потенциал производительности, однако эффективное использование этого потенциала представляет собой сложную задачу. Перечислим основные факторы, которыми определяется сложность программирования сопроцессора. Архитектура SIMD (single instruction – multiple data). Сопроцессор выполняет одни и те же команды в нескольких вычислительных секциях. Соответственно, в программе следует предусмотреть разделение данных для разных вычислительных секций и аккуратную обработку неполных (не кратных числу секций) наборов данных. Некоторые примеры программирования отражены в [1]. Суперскалярность. На каждом такте запускаются две команды: вычислительная (SIMD) и управляющая. Для их выполнения используются два конвейера, имеющих разную длину. Отсутствие аппаратных задержек по неготовности данных. Команда может прочитать значение своего входного регистра R до того, как оно было записано последней из предшествующих команд, модифицирующих R. Программист может сознательно использовать это свойство сопроцессора, чтобы считать предыдущее значение регистра. Это возможно, так как выполнение программы на сопроцессоре строго синхронно. Выполнение команды не может завершиться раньше, чем ожидается, поскольку отсутствуют какие-либо источники прерываний. Аппаратура также не отслеживает конфликты по записи, когда две команды одновременно записывают значение в один и тот же регистр, при этом результат не определен. Программист обязан учитывать эти аппаратные особенности, при необходимости вставляя в программу команды NOP. Отказ от аппаратного контроля подобных ситуаций позволяет значительно упростить сопроцессор; такое решение оправдано тем, что от запускаемых на сопроцессоре программ ожидается максимальная производительность, которая может быть достигнута только при безостановочной работе конвейера. Особенности архитектуры сопроцессора и его система команд (отсутствие ветвлений, ограниченный аппаратный стек) не позволяют реализовать для него компиляторы с языков высокого уровня; поэтому программы для CP2 разрабатываются на ассемблере. Написание ассемблерных программ, эффективно использующих вычислительные ресурсы сопроцессора, является сложной задачей, требующей больших трудозатрат и высокой квалификации разработчиков. Целью настоящей работы является реализация программной конвейери- зации внутренних циклов в программах для сопроцессора. Это позволяет программисту писать достаточно простые внутренние циклы, которые правильно реализуют вычисления, но могут быть неоптимальными. В результате конвейеризации исходный цикл трансформируется в конвейеризованный, на котором достигается максимальная или близкая к максимальной эффективность выполнения заданных программистом вычислений. Архитектурные особенности ускорителя плавающей арифметики Основные элементы CP2. Специализированный сопроцессор CP2 в составе Комдив128-РИО ориентирован на задачи обработки сигналов с пиковой производительностью 8 Гфлопс. Перечислим основные элементы CP2 (рис. 1). Четыре вычислительные секции. Каждая секция имеет свой регистровый файл, управляющие регистры и память. · Регистровый файл (FPR) состоит из 64 64-разрядных регистров. Регистр FPR может содержать два 32-битных значения с плавающей запятой (которые могут рассматриваться как вектор или как комплексное значение) или два целочисленных 32-битных значения. · Из управляющих регистров вычислительных секций в контексте данной работы существенны регистры кодов условий (FCCR), которые содержат по 8 бит кодов условий. Коды устанавливаются командами сравнения и могут использоваться предикатно исполняемыми командами. · Управляющая секция CP2, содержащая регистровый файл из 16 общих регистров (GPR). Устройство генерации адресов (AGU). Включает по 16 13-разрядных регистров адреса An, модификации Nn и режима Mn. Поле номера адресного регистра в командах чтения-записи и в командах модификации адресных регистров относится ко всем трем регистрам с указанным номером. Регистры инкрементации Nn определяют величину автоинкрементации соответствующего адресного регистра, а регистры режима адресации Mn – режим постмодификации адресного регистра. Поддерживаются режимы линейной адресации, бит-реверсной адресации и адресации по модулю (для работы с циклическими буферами). Память коэффициентов (ПЗУ) объемом 64 Кбайта. Регистры управления CP2: – PC – программный счетчик, – Comm – коммуникационный регистр для связи с управляющим процессором, – Control – регистр управления CP2, – Status – регистр состояния CP2, – PSP – указатель вершины стека подпрограмм, – LC, LA, LSP – регистры для организации циклов, – Rind, Rstep, Rmask – регистры для адресации ПЗУ, – стеки вызовов подпрограмм и организации циклов. Программная память объемом 64 Кбайта, вмещающая 213 64-разрядных командных слов. Командное слово включает VLIW-команду, содержащую одну команду управляющей секции и одну вычислительную команду, выполняющуюся на всех четырех вычислительных секциях. Каждая секция выполняет команду для данных, хранящихся в ее локальных ОЗУ и FPR. Система команд CP2. Команды сопроцессора условно разделены на две группы. Команды первой группы (арифметические операции) выполняются сразу во всех вычислительных секциях. К этой группе относятся – арифметические операции над комплексными, вещественными и целыми числами; – команды преобразования форматов данных, сравнения, а также для работы с регистрами FPR; – операция Nop. Команды второй группы (операции пересылки и управления) выполняются в управляющей секции. Эта группа команд включает – локальные обмены данными, – команды управления, – операцию Nop. VLIW-команда сопроцессора содержит две элементарные команды, принадлежащие к разным группам. Структура VLIW-команды представлена на рисунке 2. Если поле «Признаки арифметической опе- рации» ненулевое, команда первой группы выполняется условно в зависимости от значений битов регистра FCCR. Управляющие команды выполняются безусловно. Зависимости по данным и конфликты по ресурсам. Сопроцессор CP2 имеет три типа конвейеров для выполнения различных команд; длина конвейеров составляет от 3 до 8 тактов. Запись результата производится на последнем такте. Сопроцессор не отслеживает аппаратно зависимости по данным и не обеспечивает задержки по неготовности данных. Если некоторая команда требует результата предшествующей команды раньше, чем он будет записан, то используется предыдущее значение. Конфликт по ресурсам происходит, если две команды одновременно инициируют запись в один и тот же регистр. В такой ситуации результат выполнения команд не определен. Ассемблер для сопроцессора CP2 обеспечивает анализ входной программы на предмет конфликтов по ресурсам и выдает соответствующие диагностические сообщения (см. [2]). Задача программной конвейеризации циклов Метод планирования по модулю. Програм- мная конвейеризация циклов – это метод оптимизации циклов, который может давать такой же эффект, как внеочередное исполнение (out-of-order execution) команд процессором, с той разницей, что переупорядочение выполняется не аппаратурой, а компилятором (или программистом при программировании на ассемблере).
В большинстве современных компиляторов применяют метод программной конвейеризации, называемый методом планирования по модулю (modulo scheduling). Суть его в том, что для значений II из диапазона [IImin, IImax] последовательно делаются попытки построить расписание цикла, укладывающееся в II тактов. Расписание для минимального II, для которого это удалось сделать, и будет использовано при генерации кода. Как правило, построение расписаний для фиксированного II осуществляется при помощи эвристических алгоритмов, обзор которых дается в [3]. Это быстрые алгоритмы, позволяющие для универсальных целевых архитектур получать расписания, близкие к оптимальным. Однако для специализированных архитектур они не всегда дают приемлемые результаты. Поэтому для таких архитектур в условиях, когда имеются высокие требования к эффективности генерируемого кода, оправдано применение точных подходов, основанных на использовании методов математического программирования, в частности, методов целочисленного линейного программирования (ЦЛП) [4, 5]. Формулировка ЦЛП-задачи планирования циклического участка программы для сопроцессора CP2 Решением задачи должно быть расписание цикла, такое, что выполнение каждой итерации занимает заданное число тактов II и соблюдаются ограничения по числу требуемых регистров. Формулировка ЦЛП-задачи может включать входные параметры (константы), переменные, ограничения (линейные равенства и неравенства) и цель (минимизация или максимизация значения некоторой переменной). Введем необходимые параметры и переменные вместе с ограничениями, в которых они используются. Ограничения на расписание. Пусть T – множество тактов, T={0, …, II-1}; Com – множество команд в теле исходного цикла. Введем множество переменных hc(t) для всех cÎCom, tÎT. Переменная hc(t) определяет, сколько раз команда c была запущена в прологе и в первой итерации цикла до такта t включительно. Расписание запуска команд в конвейеризованном цикле однозначно задается набором переменных hc(t). Удобно доопределить отображение h: Com´T®N0 (где N0 – множество неотрицательных целых чисел) следующим макросом:
Расписание должно удовлетворять очевидным ограничениям: – количество запущенных команд не может убывать: Hc(t+1)³Hc(t) " cÎCom, " tÎT; – каждая команда запускается в прологе неотрицательное число раз: Hc(-1)³0 " cÎCom. Версии регистров. Пусть Vreg – множество виртуальных регистров, которые изменяются в цикле. Можно считать, что Hc(t) задает номер версии последней выполненной команды c. Соответственно, можно говорить о номерах версий значений виртуальных регистров из Vreg, равных но- мерам версий производящих их команд. Если в исходном цикле есть зависимости с дистанцией 1, то соответствующие входные значения вычисляются до входа в цикл и имеют номера версий, равные 0. В конвейеризованном цикле время жизни значения на регистре может быть больше II, и тогда должно храниться несколько версий этого значения. Введем три набора переменных: nv, zv, ov, связанных с версиями значений регистров (далее называемыми для простоты версиями регистров): nv, zv, ov: Vreg´T®Z. Переменная nvv(t) обозначает номер самой свежей версии значения регистра v, доступной на такте t (от 0 до II–1), то есть в первой итерации конвейеризованного цикла. Переменные zvv(t) аналогично задают номера самых свежих версий, для которых должно быть выделено место среди физических регистров. (Обычно zvv(t)>nvv(t) тогда, когда команда, вычисляющая соответствующее значение, запущена, но результат еще не вычислен.) Переменная ovv(t) определяет номер версии регистра v, которая уже недоступна на такте t первой итерации цикла (значит, и все предшествующие ей версии тоже недоступны). Переменные ovv(t) могут быть отрицательными в случае зависимостей с ненулевыми дистанциями. Аналогично (1) определяем отображения NV, ZV, OV при помощи макросов общего вида:
где x из набора (n, z, o), X из набора (N, Z, O). Для версий регистров вводятся следующие ограничения: – неубывание номеров версий со временем: XVv(t+1)³XVv(t) "vÎVreg, "tÎT, где X из набора (N, Z, O); – соотношения между версиями одного регистра: ZVv(t)³NVv(t) "vÎVreg, "tÎT; NVv(t)³OVv(t) "vÎVreg, "tÎT. Эти ограничения означают, что изготовление версии регистра происходит не раньше резервирования, а разрушение – не раньше изготовления. Ограничения, описывающие зависимости по данным. Зависимости по данным между командами цикла представляются при помощи следующих множеств: Write Ì{(c, v, wt, zt) | cÎCom, vÎVreg, wtÎZ, ztÎZ }, ReadÌ{(c, v, rt, d) | cÎCom, vÎVreg, rtÎZ, dÎZ}, DestroyÌ{(c, v, dt, d) | cÎCom, vÎVreg, dtÎZ, dÎZ}. Здесь (c, v, wt, zt)ÎWrite, если команда c записывает результат в регистр v; wt задает латентность записи; zt описывает латентность резервирования выходного регистра. Четверка (c, v, rt, d)ÎRead, если команда c читает свой аргумент из регистра v; rt задает латентность чтения данного регистра в данной команде; d определяет дистанцию зависимости: d=0, если регистр v записывается в той же итерации, и d=1, если считывается значение, записанное в предыдущей итерации. Четверка (c, v, dt, d)ÎDestroy, если команда c читает аргумент из регистра v и записывает результат в v. Значение dt задает латентность записи, d имеет тот же смысл, что и для Read. Множество Destroy описывает команды, которые записывают результат на место одного из аргументов, такие как команда инкрементации inc r1, r2, выполняющая вычисление r1=r1+r2. Такой метод представления зависимостей позволяет описывать команды, в которых некоторый регистр является входным и выходным, а также команды, имеющие более одного выходного регистра. Ключевым компонентом множеств Write и Destroy является v, то есть считается, что в каждой итерации только одна команда записывает или разрушает значение в регистре vÎVreg. Для элементов множеств Read и Destroy ключом является пара (c, v). Следующие ограничения обеспечивают соблюдение зависимостей по данным. Каждая запускаемая команда считывает свои входные значения не раньше, чем они изготовлены: NVv(t+rt)+d³Hc(t) " (c, v, rt, d)ÎRead, " tÎT. Номер последней изготовленной версии регистра v на такте t совпадает с количеством запусков команды, записывающей этот регистр, на такте t-wt: NVv(t)=Hc(t-wt) " (c, v, wt, zt)ÎWrite, " tÎT. Номер последней зарезервированной версии регистра v на такте t совпадает с количеством запусков команды, записывающей этот регистр, на такте t-zt: ZVv(t)=Hc(t-zt) " (c, v, wt, zt)ÎWrite, " tÎT. Команда должна считать требуемые ей версии входных регистров до того, как они будут разрушены: OVv(t+rt+1)£Hc(t)-d " (c, v, rt, d)ÎRead, " tÎT. В результате выполнения разрушающих команд происходит разрушение версии регистров: OVv(t+td)³Hc(t)-d "(c, v, dt, d)ÎDestroy, "tÎT. Контроль кратности развертки цикла. В конвейеризованном цикле одновременно могут существовать несколько версий виртуального регистра. Если отсутствует аппаратная ротация регистрового файла, для обеспечения отображения версий виртуального регистра на физические регистры применяют метод развертки MVE (Modulo Variable Expansion) [3]. Минимальное требуемое число версий регистра v есть maxtÎT (ZVv(t)-OVv(t)). Кратность развертки определяется как наименьшее общее кратное этих значений для всех vÎVreg. Например, если есть 3 регистра и количество их версий равно 3, 4, 5, то кратность развертки составит 60, что вряд ли приемлемо на практике. (Впрочем, можно уменьшить ее до 12, если развернуть регистры не в 5, а в 6 раз.) Для ограничения кратности развертки введем переменные lvv, задающие кратность развертки по каждому регистру. Эти переменные ограничивают сверху число одновременно хранящихся версий регистров: ZVv(t)-OVv(t)£lvv " vÎVreg, " tÎT. В условиях ЦЛП-задачи можно задать максимальную кратность развертки U и ввести ограничения на значения lvv так, чтобы они являлись делителями значения U. Например, при U=12 величины lvv должны принимать значения 1, 2, 3, 4, 6, 12. Существует стандартный способ задания принадлежности значения переменной фиксированному множеству. Далее вводятся переменные и ограничения, при помощи которых обеспечивается это условие. Введем массив переменных dvsv(d), принимающих значение 0 или 1, где vÎVreg, dÎ{d: d|U}. Здесь запись d|U означает, что d является делителем U. Равенство dvsv(d)=1 свидетельствует, что lvv=d, то есть регистр v развернут в d раз. Следующие ограничения необходимы и достаточны для выполнения условий на значения переменных lvv: Ограничения по числу доступных регистров. Пусть TP – множество классов регистров процессора. Так, например, в циклах для CP2 могут использоваться регистры следующих классов: FPR2 – парные регистры FPR (128 бит), FPR (64 бита) – регистры FPR, FPRH (32 бита) – старшие половины регистров FPR, FPRL (32 бита) – младшие половины регистров FPR, FCCR – регистры кодов условий, An – регистры адреса, Nn – регистры модификации, Mn – регистры режима. Определим Pv,tp как стоимость регистра v в классе tp Î TP. Например, стоимость регистра FPR2 составляет 1 в классе FPR2, 2 в классах FPR, FPRH, FPRL и 0 в остальных классах. Тогда ограничения по числу доступных регистров записываются следующим образом:
где nreg(tp) – число регистров класса tp. Ограничения по ресурсам (например, ограничение на число команд, запукаемых на каждом такте) в данной задаче аналогичны рассмотренным в работе [5]. Ограничения, связанные со спецификой CP2 Приведенная выше формулировка ЦЛП-задачи планирования циклических участков кода в целом эквивалентна формулировке, представленной в работе [5], и может быть использована для универсальных процессоров. По сравнению с [5] в ней изменен учет зависимостей и явно введены версии виртуальных регистров для упрощения описаний рассматриваемых далее ограничений, связанных со следующими особенностями сопроцессора CP2: – отсутствие аппаратных задержек по неготовности регистра или конфликтам по ресурсам; – условное выполнение арифметических команд; – контейнерная структура регистрового файла: команды CP2 могут читать или записывать пары соседних регистров, один регистр, старшую или младшую 32-битную часть регистра, что существенно с точки зрения учета зависимостей по данным и при подсчете числа требуемых регистров. Отметим, что отсутствие аппаратных задержек не усложняет, а упрощает формулировку задачи конвейеризации, так как позволяет отождествить задержки захвата регистра с задержкой записи. Описание условных команд основано на следующей идее: вычисление if(cond) a:=f(b, c) можно заменить на a:=(cond)?f(b, c): a, где условный оператор ?: рассматривается как обычная функция с тремя аргументами. Таким образом, условное выполнение арифметических команд может быть описано в определенных выше терминах следующим образом: – условная команда является читателем всех регистров, которые читает соответствующая безусловная команда, а также читает регистр условия; – дополнительно условная команда считается читателем всех выходных регистров, причем задержка чтения задается на 1 меньше задержки записи (то есть условная команда как бы читает старое значение перед безусловной записью нового); – условная команда должна быть не просто читателем выходных регистров, а последним читателем, как и команды с входными-выходными (in/out) аргументами, описанные в множестве Destroy. Более сложные проблемы возникают с составными регистрами, к компонентам которых происходят обращения как по отдельности, так и совместно. Выделим в множестве Vreg подмножества Vsimple (простые регистры), Vinner (вложенные регистры), Vcont (регистры-контейнеры). Vreg=VsimpleÈVinnerÈVcont. Регистры Vcont не входят в зависимости. Переменные lvv вводятся только для VsimpleÈVcont: Отображение Cont(v) ставит в соответствие регистру vÎVinner содержащий его регистр-контейнер. Заметим, что регистры-контейнеры также могут быть развернуты, то есть одновременно могут сосуществовать несколько их версий. Возникает вопрос о связи версий контейнеров и версий вложенных в них регистров. Версия вложенного регистра однозначно определяется версией контейнера, причем номер версии контейнера должен получаться из номера версии вложенного регистра прибавлением некоторого смещения. Введем переменные Shiftv, определяющие сдвиг между версиями внутреннего регистра и его регистра-контейнера, и опишем общие ограничения для этих переменных: ZVv(t)+Shiftv≤ZVCont(v)(t), OVv(t)+Shiftv³OVCont(v)(t), "vÎVinner, "tÎT. Некоторые команды обращаются одновременно к нескольким вложенным регистрам одного контейнера. Необходимо, чтобы соответствующие версии вложенных регистров находились в одном и том же физическом регистре, то есть должны совпадать версии их регистра-контейнера с точностью до кратности развертки этого конвейера. Для этого определим три множества: Pwrite, Pread, Pread_write, описывающие команды, которые работают с двумя или более вложенными регистрами одного контейнера. Pwrite описывает множество команд, пишущих одновременно в два или более вложенных регистра одного контейнера: Pwrite Ì{(c, v1, v2) | cÎCom, v1ÎVinner, v2ÎVinner, Cont(v2)=Cont(v2)}. Аналогичным образом определяется множество Pread, описывающее команды, которые читают два или более вложенных регистра, и множество Pread_write, описывающее команды, которые читают v1ÎVinner и пишут v2ÎVinner, где Cont(v1)= =Cont(v2). Пусть (с, v1, v2)ÎPwrite. Тогда существуют (c, v1, wt1, zt1)ÎWrite, (c, v2, wt2, zt2)ÎWrite. Пусть cnt=Cont(v1)=Cont(v2). Должно выполняться ограничение Shiftv1@Shiftv2(mod lvcnt). Заметим, что данное равенство не является линейным, так как представляет собой равенство по модулю переменной. Действительно, a@b(mod l) эквивалентно a=b+k*l, где k – переменная. Если l –переменная, то k*l – нелинейный член. Тем не менее, если a–b можно ограничить по абсолютной величине, то можно применить технику, подобную той, которая использовалась выше при определении переменных lvv. Сравнение по модулю необходимо, так как, с одной стороны, версии регистра, отличающиеся на коэффициент развертки, располагаются в одном физическом регистре, с другой стороны, существуют примеры циклов, в которых при задании точного равенства не удастся построить ни одного расписания ни при каком II. Пусть (с, v1, v2)ÎPread. Тогда существуют (c, v1, rt1, d1)ÎRead, (c, v2, rt2, d2)ÎRead. Пусть cnt=Cont(v1)=Cont(v2). Должно выполняться ограничение Shiftv1-d1@Shiftv2-d2 (mod lvcnt). Пусть (с, vr, vw)ÎPread_write. Тогда существуют (c, vr, rt, d)ÎRead, (c, vw, wt, zt)ÎWrite. Пусть cnt=Cont(v1)=Cont(v2). Должно выполняться ограничение Shiftvr-d@Shiftv2(mod lvcnt). Есть еще одна проблема, связанная со сложными регистрами: могут быть использованы вложенные в один контейнер виртуальные регистры, пересекающиеся между собой как части контейнера. Очевидный пример: последовательное изменение компоненты сложного регистра дает разные виртуальные регистры, лежащие в одном месте контейнера. Естественно, они не могут сосуществовать одновременно. Точнее, не могут сосуществовать их версии, относящиеся к одной версии контейнера. Хорошего решения данной проблемы в настоящий момент нет, а в качестве необходимого (но, возможно, недостаточного) условия используется то, что для каждого множества пересекающихся регистров сумма числа их существующих версий (ZVv - OVv) на любом такте не превышает числа существующих версий регистра-контейнера. Цель задачи в принципе необязательна. Тем не менее цель можно определить как минимизацию суммы разностей ZVv(t)-OVv(t) (числа одновременно хранящихся версий виртуальных регистров) по всем vÎVreg, tÎT. Это полезно, потому что иначе, при избытке регистров, генерируется избыточное расписание, в котором за счет использования большего числа регистров время жизни значений намного больше необходимого. При этом одни значения могут храниться, когда они уже не нужны ни одной команде, другие используются неоправданно поздно. Введение указанной цели позволяет генерировать программы, более простые для изучения, а также способствует снижению кратности развертки тела цикла при применении метода MVE. Пример конвейеризации цикла для сопроцессора CP2 Рассмотрим цикл, в котором каждый элемент вектора X, находящийся в заданном диапазоне, записывается в выходной массив Y, иначе в выходной массив записываются специальные константы: for(i = 0; i < n; i++) { if ( x[i] <= min_x ) y[i] = c1; else if ( x[i] >= max_x) y[i] = c2; else y[i] = x[i]; } Этот цикл может быть записан на языке ассемблера для CP2 следующим образом: do g0, Loop lw f1,(r1)+1 ## Чтение по адресу r1 в регистр f1 ## с постинкрементом регистра r1 nop ;; nop ;; nop c.le.ps 2,f1,f60 ## f1 <= f60(min,min) c.ge.ps 4,f1,f61 ## f1 >= f61(max,max) psprmsgn f10, f0, 0x0, 0x27 ## f10 = (0,x1) f11 = (0,x2) nop;; nop ;; nop ;; nop ;; nop ;; nop if(2) copy f11, f62 ## Если младшая половина регистра ## удовлетворяет условию if(3) copy f10, f62 ## Если старшая половина регистра ## удовлетворяет условию if(4) copy f11, f63 ## Если младшая половина регистра ## удовлетворяет условию if(5) copy f10, f63 ## Если старшая половина регистра ## удовлетворяет условию nop;; nop ;; nop ;; nop ;; nop ;; nop ;; nop psprmsgn f20, f10, 0x0, 0x27 nop ;; nop ;; nop Loop: sw f21,(r2)+1 Здесь на каждом такте запускается только одна команда, хотя можно запустить и две: арифметическую и управляющую. Кроме того, в программе присутствует большое число команд nop, необходимых для того, чтобы успели вычислиться аргументы следующей команды. Выполнение каждой итерации цикла занимает 29 тактов. После конвейеризации (с разверткой в 2 раза) получается следующее развернутое тело цикла:
Одна итерация конвейеризованного цикла занимает 12 тактов, то есть 6 тактов вместо 29 на один обрабатываемый элемент, что дает ускорение почти в 5 раз. Отметим высокую плотность полученного кода: отсутствие команд nop и большое число параллельно запущенных команд. В данном примере развертка в 2 раза вызвана тем, что многие регистры (которые следует рассматривать как виртуальные) были развернуты в 2 раза. В листинге это отражено в виде скобок после имени регистра: например, регистрам f11(0) и f11(1) должны соответствовать два разных физических регистра. Такой синтаксис был выбран, чтобы использовать для этой замены препроцессор, определив имена развертываемых регистров (f11) как макросы. Осталось заметить, что в этом примере присутствуют сложные регистры, так как команды psprmsgn оперируют парами последовательных регистров (хотя это не отражено в синтаксисе команды). Таким образом, условные команды копирования модифицируют компоненты составных значений. В заключение можно сделать следующие выводы. Представленная в работе формулировка ЦЛП-задачи планирования циклов позволяет учитывать ряд свойств системы команд и архитектурных решений, используемых в аппаратных ускорителях. Описание условно исполняемых команд основано на определении условной операции как операции, сливающей старое и новое значения выходного регистра, и на аккуратном определении задержек чтения и задержек разрушения. Наибольшие сложности возникают при описании работы со сложными регистрами, допускающими чтение и запись отдельных компонент (те же проблемы возникают при описании команд, оперирующих парами последовательных регистров). Подобные архитектурные особенности широко распространены не только в сопроцессоре CP2: всевозможные операции, оперирующие старшими и младшими половинами целочисленного регистра, младшим байтом регистра, парами последовательных регистров с плавающей точкой, отдельными битами статус-регистра или компонентами вектора в векторных расширениях. Более того, любая арифметическая команда в традиционных процессорах модифицирует отдельные (необязательно все) биты условия (Z, N, O, C, ...), оперируя регистром условий как составным регистром. Для этих случаев предложена модель виртуальных регистров-контейнеров с вложенными в них виртуальными регистрами. В формулировке также предусмотрены возможности для ограничения кратности развертки циклов при применении метода MVE, что существенно для архитектур, не имеющих аппаратных средств ротации регистрового файла. Литература 1. Лесных А.А., Широков И.А. Оценки производительности суперЭВМ на основе сопроцессора вещественной арифметики на задачах обработки сигналов. М.: НИИСИ РАН, 2005. С. 20–49. 2. Ассемблер для специализированного сопроцессора (CP2) в составе микропроцессора Комдив128-РИО: руководство программиста. М.: НИИСИ РАН, 2011. 3. Вьюкова Н.И., Галатенко В.А., Самборский С.В. Программная конвейеризация циклов методом планирования по модулю // Программирование. 2007. № 6. С. 14–25. 4. Stoutchinin A. An Integer Linear Programming Model of Software Pipelining for the MIPS R8000 Processor, Proc. 4th Intern. Conf. on Parallel Computing Technologies (PaCT '97), 1997, September, pp. 121–135. 5. Самборский С.В. Формулировка задачи планирования линейных и циклических участков кода // Программные продукты и системы. 2007. № 3 (79). С. 12–16. References 1. Lesnykh A.A., Shirokov I.A. Otsenki proizvoditelnosti superEVM na osnove soprotsessora veshchestvennoy arifmetiki na zadachakh obrabotki signalov [Benchmark test of super computer based on floating point arithmetics coprocessor for signal processing construct]. Moscow, NIISI RAN Publ., 2005, pp. 20–49. 2. Assembler dlya spetsializirovannogo soprotsessora (CP2) v sostave mikroprotsessora Komdiv128-RIO: rukovodstvo programmista [Assembler for specialized coprocessor (CP2) in Komdiv128-RIO microprocessor: programmer's manual]. Moscow, NIISI RAN Publ., 2011. 3. Vyukova N.I., Galatenko V.A., Samborskiy S.V. Software pipelining of loops by planning with module. Programmirovanie [Programming]. Moscow, iss. 6, 2007, pp. 14–25 (in Russ.). 4. Stoutchinin A. An Integer Linear Programming Model of Software Pipelining for the MIPS R8000 Processor. Proc. of the 4th int. conf. on parallel computing technologies (PaCT '97), 1997, pp. 121–135. 5. Samborskiy S.V. Formulirovka zadachi planirovaniya lineynykh i tsiklicheskikh uchastkov koda [Formulation of the linear and cyclic codes planning task]. Programmnye produkty i sistemy [Software & Systems]. 2007, vol. 79, iss. 3, pp. 12–16. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3655 |
Версия для печати Выпуск в формате PDF (7.95Мб) Скачать обложку в формате PDF (1.45Мб) |
| Статья опубликована в выпуске журнала № 4 за 2013 год. [ на стр. 35-43 ] |
Назад, к списку статей



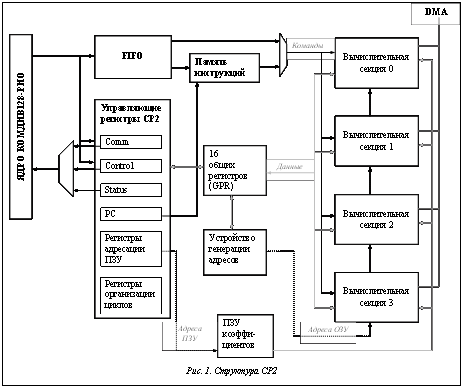 Память данных (ОЗУ) имеет объем 64 Кбайта (213 64-разрядных слов).
Память данных (ОЗУ) имеет объем 64 Кбайта (213 64-разрядных слов). Результатом программной конвейеризации является цикл, который выполняет те же вычис- ления, что исходный, и совмещает в своем теле команды, относящиеся к разным итерациям исходного цикла. За счет такого совмещения обеспечивается скрытие латентностей команд и достигается эффективное использование параллелизма на уровне команд, присущего современным микропроцессорным архитектурам. Время выполнения конвейеризованного цикла (в тактах) называют обычно основным интервалом, или интервалом запуска, и обозначают II (Initiation Interval). Для обеспечения эквивалентности конвейеризованного цикла исходному перед входом в цикл и после выхода из него добавляются пролог и эпилог, в которых исполняются команды из соответственно начальных и конечных итераций исходного цикла. Кроме того, должно быть скорректировано число повторений цикла. Подробнее эти и другие аспекты генерации кода для конвейеризованных циклов описаны в [3].
Результатом программной конвейеризации является цикл, который выполняет те же вычис- ления, что исходный, и совмещает в своем теле команды, относящиеся к разным итерациям исходного цикла. За счет такого совмещения обеспечивается скрытие латентностей команд и достигается эффективное использование параллелизма на уровне команд, присущего современным микропроцессорным архитектурам. Время выполнения конвейеризованного цикла (в тактах) называют обычно основным интервалом, или интервалом запуска, и обозначают II (Initiation Interval). Для обеспечения эквивалентности конвейеризованного цикла исходному перед входом в цикл и после выхода из него добавляются пролог и эпилог, в которых исполняются команды из соответственно начальных и конечных итераций исходного цикла. Кроме того, должно быть скорректировано число повторений цикла. Подробнее эти и другие аспекты генерации кода для конвейеризованных циклов описаны в [3]. "cÎCom. (1)
"cÎCom. (1) "vÎVreg,
"vÎVreg, "vÎVreg,
"vÎVreg, 
 "vÎVreg.
"vÎVreg. "tpÎTP,
"tpÎTP,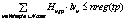 "tpÎTP.
"tpÎTP.