Практика и результаты моделирования реальных объектов показали, что в условиях неопределенности или неточности исходной информации, непредвиденных ситуаций или информационного риска традиционный (использующий принцип глобальной отрицательной обратной связи) и широко применяемый в промышленности ПИД-регулятор часто не справляется с поставленной задачей управления. В то же время задача глобальной робастности ПИД-регулятора до настоящего времени не решена, несмотря на актуальность данной проблемы.
Использование нечетких регуляторов (НР) совместно с ПИД-регулятором привело к созданию гибридных нечетких интеллектуальных систем управления (ИСУ) с различными уровнями интеллектуальности в зависимости от полноты и корректности спроектированной БЗ. Применение технологии мягких вычислений (основанной на ге- нетических алгоритмах и нечетких нейронных сетях) расширило область эффективного применения НР за счет добавления новых функций в виде обучения и адаптации. Однако в общем случае нештатных ситуаций управления очень трудно спроектировать глобально «хорошую» и робастную структуру ИСУ. Данное ограничение особенно характерно для непредвиденных ситуаций управления, когда объект управления (ОУ) функционирует в резко изменяющихся условиях (отказ датчиков или шум в измерительной системе, наличие времени задержки сигналов управления или измерения, резкое изменение структуры ОУ или ее параметров и т.п.).
Решение такого рода проблем может быть найдено на основе введения принципа самоорганизации БЗ в процесс проектирования НР, который реализуется и программно поддерживается разработанной моделью квантового нечеткого вывода (КНВ) с применением методологии квантовых мягких вычислений и системной инженерией – System of System Engineering (синергетический принцип самоорганизации) [1, 2].
 Предлагаемая модель КНВ использует частные индивидуальные БЗ НР, каждая из которых получается с помощью оптимизатора БЗ (ОБЗ) на мягких вычислениях для соответствующих условий функционирования ОУ и фиксированных ситуаций управления во внешней случайной среде. Проектирование частных индивидуальных БЗ НР с помощью программного инструментария ОБЗ для заданных ситуаций управления осуществляется в соответствии с технологией проектирования ИСУ и подробно рассмотрен в [3].
Предлагаемая модель КНВ использует частные индивидуальные БЗ НР, каждая из которых получается с помощью оптимизатора БЗ (ОБЗ) на мягких вычислениях для соответствующих условий функционирования ОУ и фиксированных ситуаций управления во внешней случайной среде. Проектирование частных индивидуальных БЗ НР с помощью программного инструментария ОБЗ для заданных ситуаций управления осуществляется в соответствии с технологией проектирования ИСУ и подробно рассмотрен в [3].
Структура и основные функции КНВ
Основной задачей, решаемой КНВ, является формирование БЗ с повышенным уровнем робастности из конечного множества БЗ для НР, сформированных с применением технологии мягких вычислений. Рассмотрим кратко функциональную структуру и работу основных блоков КНВ. В качестве примера, без потери общности результата, обсудим процессы извлечения скрытой квантовой информации, обработки данных и формирования робастной БЗ НР, используя БЗ двух НР, спроектированных для фиксированных (отличных друг от друга) ситуаций управления.
На р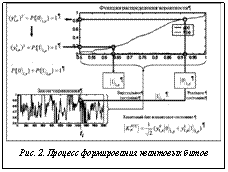 исунке 1 показана функциональная структура модели КНВ. На вход КНВ в реальном времени поступают сигналы управления от сфор- мированных заранее БЗ НР (шаг «Начальное состояние»). Следующим шагом является процесс нормализации полученных сигналов в интервале [0 1] путем деления амплитуд траектории сигналов управления на максимальные амплитуды. После нормировки сигналов осуществляется формирование квантовых битов из текущих значений нормированных сигналов управления. С этой целью предварительно определяется функция плотности распределения вероятности по представленным выборочным траекториям сигналов управления.
исунке 1 показана функциональная структура модели КНВ. На вход КНВ в реальном времени поступают сигналы управления от сфор- мированных заранее БЗ НР (шаг «Начальное состояние»). Следующим шагом является процесс нормализации полученных сигналов в интервале [0 1] путем деления амплитуд траектории сигналов управления на максимальные амплитуды. После нормировки сигналов осуществляется формирование квантовых битов из текущих значений нормированных сигналов управления. С этой целью предварительно определяется функция плотности распределения вероятности по представленным выборочным траекториям сигналов управления.
Далее путем интегрирования полученной функции плотности распределения вероятности определяются интегральные функции распределения вероятностей. Полученные таким образом функции распределения вероятности позволяют выделить виртуальные состояния |1ñ сигналов управления для формирования суперпозиции с помощью преобразования Адамара из текущего состояния введенных сигналов управления. При этом используется закон вероятности типа P(|0ñ)+ P(|1ñ)=1, где P|0ñ и P|1ñ – вероятности текущего реального и виртуального состояний сигнала управления соответственно. Для текущего реального нормированного состояния сигнала управления |0ñ с помощью интегральной функции распределения вероятности определяется его вероятность. Далее из закона сохранения вероятностей рассчитывается вероятность виртуального состояния сигнала управления. Используя тот же интегральный закон распределения вероятностей, путем обратного отображения можно вычислить численное значение соответствующего виртуального состояния сигнала управления.
Следовательно, суперпозиция квантовой системы «реальное состояние–виртуальное состояние» имеет следующий вид:
 =квантовый бит.
=квантовый бит.
 На рисунке 2 схематично отображены вычислительный процесс и формирование квантового бита для текущего состояния нормированного сигнала управления, описывающего коэффициенты усиления нечеткого ПИД-регулятора в структуре ИСУ.
На рисунке 2 схематично отображены вычислительный процесс и формирование квантового бита для текущего состояния нормированного сигнала управления, описывающего коэффициенты усиления нечеткого ПИД-регулятора в структуре ИСУ.
Далее осуществляется выбор типа квантовой корреляции (рис. 1) из соответствующих компонент для используемого типа корреляции из нормированных сигналов управления. Для рассматриваемой ситуации возможны три типа квантовой корреляции (содержащих скрытую в спроектированных БЗ ценную квантовую информацию): пространственная, временная и пространственно-временная.
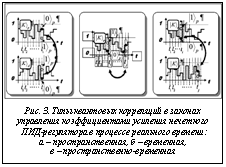
На рисунке 3 показаны перечисленные типы корреляции между процессами управления коэффициентами усиления двух нечетких ПИД-регуляторов.
 На рисунке 4 приведен пример формирования пространственной корреляции в КНВ из сигналов управления коэффициентами усиления двух нечетких ПИД-регуляторов, БЗ которых спроектированы с помощью инструментария ОБЗ для двух различных ситуаций управления.
На рисунке 4 приведен пример формирования пространственной корреляции в КНВ из сигналов управления коэффициентами усиления двух нечетких ПИД-регуляторов, БЗ которых спроектированы с помощью инструментария ОБЗ для двух различных ситуаций управления.
Согласно рисунку 4, квантовая пространственная корреляция (как тип) классифицируется, в свою очередь, на два вида корреляций: внутренняя и внешняя. Внутренняя корреляция формируется за счет установления статистических взаимосвязей между выходными сигналами управления коэффициентами усиления заданного первого НР типа KFC1. Внешний вид корреляции характеризует связь между соответствующими сигналами управления первого KFC1 и второго KFC2 НР, где индекс FC1 означает нечеткий регулятор 1 (НР1), а индекс FC2 – нечеткий регулятор 2 (НР2).
Отметим также, что аналогичные рассуждения справедливы для временной и пространственно-временной корреляций. В результате формирования таких типов и видов квантовой корреляции осуществляется координационное управление между коэффициентами усиления за счет соответствующей внутренней и внешней силы корреляции. Следовательно, для конкретного рассматриваемого случая двух НР каждое квантовое состояние суперпозиции выбранного коэффициента усиления описывается четырьмя квантовыми битами.
Рассмотрим алгоритм формирования суперпозиции (рис. 1) для вычисления оптимального значения, например, пропорционального коэффициента усиления нечеткого ПИД-регулятора, используя БЗ двух НР из разных ситуаций управления. Остальные коэффициенты вычисляются по аналогичному алгоритму.
Пример вычисления искомого множества значений пропорционального коэффициента усиления из множества комбинаций 
 выглядит следующим образом:
выглядит следующим образом:

Здесь  – используемое значение сигналов управления пропорциональным коэффициентом усиления БЗ первого НР, спроектированного для первой фиксированной ситуации управления;
– используемое значение сигналов управления пропорциональным коэффициентом усиления БЗ первого НР, спроектированного для первой фиксированной ситуации управления;  – значение сигналов управления дифференциальным коэффициентом усиления БЗ второго НР, разработанного для второй ситуации управления (существенно отличающейся от первой по внешним условиям функционирования ОУ).
– значение сигналов управления дифференциальным коэффициентом усиления БЗ второго НР, разработанного для второй ситуации управления (существенно отличающейся от первой по внешним условиям функционирования ОУ).
Применяя тензорное произведение между преобразованиями Адамара, получим члены вида  и аналогичные комбинации коэффициентов усиления. Как видно из обозначений, имеется 16 возможных состояний, описывающих комбинации корреляций (с учетом их типа и вида) между соответствующими коэффициентами усиления двух НР, спроектированных для разных ситуаций управления.
и аналогичные комбинации коэффициентов усиления. Как видно из обозначений, имеется 16 возможных состояний, описывающих комбинации корреляций (с учетом их типа и вида) между соответствующими коэффициентами усиления двух НР, спроектированных для разных ситуаций управления.
Следует отметить принципиальную особенность процесса формирования и проектирования нового вида робастных коэффициентов усиления нечеткого ПИД-регулятора за счет применения квантового оператора суперпозиции. Новые типы и виды квантовой корреляции позволяют осу- ществить координационное управление коэффициентами усиления только за счет физических ресурсов используемого вида корреляции. Это приводит к сжатию и устранению (редукции) избыточности информации в независимых законах управления коэффициентами усиления, извлечению наиболее ценной информации и, как следствие, к повышению уровня робастности новой спроектированной БЗ за счет нового вида координации. Применение запутанных состояний в трех типах корреляции дает возможность повысить уровень робастности спроектированной БЗ (с помощью физических свойств запутанных состояний), используя эффект обмена информацией между квантовыми состояниями в сформированной суперпозиции (см. рис. 1). Такой подход к проектированию робастных БЗ не имеет классических аналогов и отличается чисто квантовой природой получаемых эффектов проектирования.
Напомним, что квадрат амплитуды вероятностей состояния в квантовой механике равен классической вероятности нахождения квантовой системы в данном состоянии (постулат Бора, который имеет несколько вариантов строгого обоснования [4]).
 С точки зрения квантовой теории информации чистое квантовое состояние характеризуется, как известно, нулевым значением энтропии фон Неймана. Следовательно, интеллектуальное квантовое состояние в рассматриваемом КА имеет место для минимума информационной энтропии квантового состояния Шеннона. Искомый минимум достигается, в свою очередь, при максимуме вероятности состояния (по определению информационной энтропии квантового состояния Шеннона
С точки зрения квантовой теории информации чистое квантовое состояние характеризуется, как известно, нулевым значением энтропии фон Неймана. Следовательно, интеллектуальное квантовое состояние в рассматриваемом КА имеет место для минимума информационной энтропии квантового состояния Шеннона. Искомый минимум достигается, в свою очередь, при максимуме вероятности состояния (по определению информационной энтропии квантового состояния Шеннона  , то есть глобальный минимум наблюдается при максимуме вероятности Pi). Так как Pi по определению есть квадрат соответствующей амплитуды вероятностей, принцип максимума амплитуды вероятностей при коррелированном состоянии может быть принят за критерий отбора приоритетного «интеллектуального» корреляционного (когерентного) состояния в суперпозиции возможных кандидатов [5, 6].
, то есть глобальный минимум наблюдается при максимуме вероятности Pi). Так как Pi по определению есть квадрат соответствующей амплитуды вероятностей, принцип максимума амплитуды вероятностей при коррелированном состоянии может быть принят за критерий отбора приоритетного «интеллектуального» корреляционного (когерентного) состояния в суперпозиции возможных кандидатов [5, 6].
 Таким образом, вычислением амплитуд квантовых состояний в суперпозиции состояний со смешанными видами квантовой корреляции (рис. 1) и выбором среди них максимальной реализуется модель квантового оракула, обладающего (по определению понятия квантового оракула) необходимой информацией об искомом решении.
Таким образом, вычислением амплитуд квантовых состояний в суперпозиции состояний со смешанными видами квантовой корреляции (рис. 1) и выбором среди них максимальной реализуется модель квантового оракула, обладающего (по определению понятия квантового оракула) необходимой информацией об искомом решении.
С помощью стандартной процедуры декодирования (внутреннего произведения векторов в гильбертовом пространстве) и выбора коэффициентов шкалирования для выходных значений проектируемых коэффициентов усиления (рис. 1) осуществляется итерационная работа КА КНВ. Дистанционное подключение ОУ к стационарной вычислительной системе открывает возможность удаленной настройки, формирования и самоорганизации БЗ НР в режиме реального времени.
Приведенная модель КА для КНВ позволяет решать классические проблемы проектирования робастных БЗ НР в структурах ИСУ, не имеющих аналогов решений среди семейства рандомизированных классических алгоритмов, и отличается полиномиальной вычислительной сложностью (BQP – класс вычислительной сложности) [7].
Квантовые вычисления на классическом процессоре: применение в робастном управлении неустойчивым ОУ
Проектирование системы управления на основе КНВ осуществляется с использованием разработанного программного инструментария «Квантовый оптимизатор» [1, 8]. Технология применения КНВ позволяет объединять в единую систему управления несколько БЗ, тем самым позволяя нечетким нейронным сетям работать параллельно.
 Для демонстрации возможностей технологии квантовых вычислений используем классическую задачу теории управления «каретка – перевернутый маятник». Одно из решений данной задачи – ПИД-регулятор в контуре обратной связи. Согласно [9–12], в качестве нижнего исполнительного уровня традиционный ПИД-регулятор и его модификации используются более чем в 85 % контуров управления в промышленных и непромышленных структурах САУ, включая объекты с повышенной социально-экономической ответственностью. Настройка и проектирование регулятора осуществляются как экспертом, так и различными программами. Обычно при проектировании используют интеллектуальные технологии, и этому посвящено множество работ, например [13, 14]. В основном в них рассматриваются создание и обучение нейронных сетей или БЗ с использованием различных алгоритмов обучения. В отличие от этих работ в данном эксперименте рассмотрим возможность применения КНВ для объединения БЗ, полученных на основе обучающего сигнала с физического объекта (ГА-ПИД-регулятор) и верифицированной математической модели [3] (рис. 5). В таблице 1 приведено сравнение БЗ, используемых для формирования КНВ.
Для демонстрации возможностей технологии квантовых вычислений используем классическую задачу теории управления «каретка – перевернутый маятник». Одно из решений данной задачи – ПИД-регулятор в контуре обратной связи. Согласно [9–12], в качестве нижнего исполнительного уровня традиционный ПИД-регулятор и его модификации используются более чем в 85 % контуров управления в промышленных и непромышленных структурах САУ, включая объекты с повышенной социально-экономической ответственностью. Настройка и проектирование регулятора осуществляются как экспертом, так и различными программами. Обычно при проектировании используют интеллектуальные технологии, и этому посвящено множество работ, например [13, 14]. В основном в них рассматриваются создание и обучение нейронных сетей или БЗ с использованием различных алгоритмов обучения. В отличие от этих работ в данном эксперименте рассмотрим возможность применения КНВ для объединения БЗ, полученных на основе обучающего сигнала с физического объекта (ГА-ПИД-регулятор) и верифицированной математической модели [3] (рис. 5). В таблице 1 приведено сравнение БЗ, используемых для формирования КНВ.
Таблица 1
Сравнение БЗ
|
Параметр
|
БЗ1 Модель (FC1)
|
БЗ2 Макет (FC4)
|
|
Количество правил
|
245
|
270
|
|
Количество функций принадлежности
|
8´6´6
|
5´8´8
|
|
Способ оптимизации
|
Моделирование
|
Дистанционная настройка
|
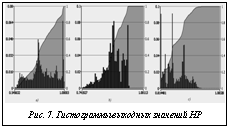
Перед тем как приступить к созданию квантового НР, необходимо получить гистограммы распределения выходных сигналов (коэффициентов усиления) нечетких регуляторов (рис. 6).
Для этого проводится серия экспериментов и моделирования в типовой ситуации управления. Используя полученные значения коэффициентов усиления при работе модели и макета, сформируем массив данных для построения гистограмм коэффициентов усиления ПИД-регуляторов (рис. 7).
Построение гистограмм происходит автоматически при загрузке данных в квантовый оптимизатор БЗ. В дальнейшем они используются в алгоритме КНВ для формирования виртуальных состояний. Гистограммы коэффициентов усиления, полученные экспериментально, используются в формировании КНВ для робота (в физическом эксперименте); гистограммы коэффициентов усиления, полученные с использованием математической модели, применяются в формировании КНВ для моделирования. После загрузки данных выбирается вид квантовой корреляции между коэффициентами усиления. Формирование запутанных состояний осуществляется на основе выбранной корреляционной матрицы, которая устанавливается в рабочем окне оптимизатора.
На следующем шаге устанавливаются соответствующие максимальные и минимальные значения для входных и выходных сигналов КНВ и осуществляется настройка шкалирующих коэффициентов (рис. 1). Планируется использовать математическую модель или дистанционное подключение к объекту управления, то есть дополнительного оборудования для приема-передачи данных, например, радиоканал Bluetooth, Wi-Fi или подключение по кабелю, например USB. Предполагается обмен информацией между ОУ и квантовым оптимизатором для поиска шкалирующих коэффициентов (рис. 1) квантового регулятора. В результате проектирования выходной сигнал из блока КНВ применяется для управления коэффициентами усиления ПИД-регулятора в случае моделирования математической модели, а для робота в физическом эксперименте применяется экспортируемый файл с расширением «*.с».
Моделирование и эксперимент
Рассмотрим применение разработанной модели КНВ для формирования процесса управления коэффициентами усиления нечеткого ПИД-регулятора. Для этого проведем компьютерное моделирование и эксперимент для двух ситуаций управления:
– в первой (типовой) ситуации (С1) задержка управляющего сигнала стандартная – 0,01 сек.;
– во второй (непредвиденной) ситуации (С2) задержка управляющего сигнала – 0,04 сек. (увеличенная в четыре раза).
В таблице 2 представлены параметры математической модели [3] для С1 и С2.
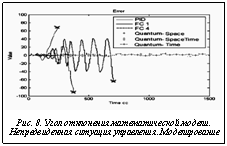
На рисунке 8 представлены результаты моделирования в непредвиденной ситуации управления.
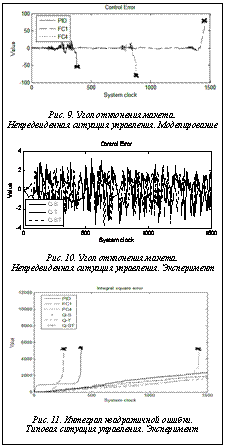
Рассмотрим результаты эксперимента в непредвиденной ситуации управления (С2). Рисунки 9–11 иллюстрируют результаты экспериментов в непредвиденных и типовой ситуациях управления.
Оценка управления показала, что НР, разработанные с использованием ОБЗ, обеспечивают систему более простым управлением, что в итоге положительно сказывается на сроке использования оборудования, повышении надежности, снижая износ и энергопотребление. Разработанная методология объединения стратегий управления на основе КНВ позволяет эффективно справляться с задачами управления и в нештатных ситуациях, в которых с задачей управления не справляются НР, спроектированные на ситуациях обучения.
Таблица 2
Ситуации управления и параметры математических моделей
|
Параметр
|
С1
|
С2
|
|
Начальный угол
|
0 гр.
|
0 гр.
|
|
Начальная скорость
|
1 гр./сек.
|
1 гр./сек.
|
|
Масса тележки
|
0,56 кг
|
0,56 кг
|
|
Масса маятника
|
0,63 кг
|
0,63 кг
|
|
Длина маятника
|
0,05 м
|
0,07 м
|
|
Трение в креплении
|
3,55 + нормированный шум с интенсивностью 0,01 и амплитудой 0,35
|
3,73 + нормированный шум с интенсивностью 0,01 и амплитудой 0,35
|
|
Трение колес
|
3,63 + гауссовский шум 15 %
|
3,63 + гауссовский шум 15 %
|
|
Сила упругости
|
5,54 Н/м
|
5,54 Н/м
|
|
Шум в системе управления
|
Равномерный [-2,15 2,15], интенсивность 0,48
|
Равномерный [-2,15 2,15], интенсивность 0,48
|
|
Шум в системе измерения
|
Амплитуда 0,22, гауссовский шум, интенсивность 0,01
|
Амплитуда 0,32, гауссовский шум, интенсивность 0,01
|
|
Задержка управляющего воздействия
|
0,01 сек.
|
0,04 сек.
|
 Таким образом, имеем новый синергетический эффект за счет квантовой самоорганизации знаний: спроектированный на основе КНВ интел- лектуальный регулятор справляется в нештатной ситуации с поставленной задачей управления и имеет робастную БЗ, в основе проектирования которой лежат неробастные БЗ (см. рис. 9 и 11). В этом случае имеем новый синергетический эффект в теории искусственного интеллекта: из двух необученных классических автоматов можно спроектировать новый интеллектуальный квантовый автомат. Причем система управления на основе КНВ наследует лучшие характеристики качества управления от БЗ спроектированных ранее нечетких регуляторов, добавляя способность к самоорганизации в реальном времени.
Таким образом, имеем новый синергетический эффект за счет квантовой самоорганизации знаний: спроектированный на основе КНВ интел- лектуальный регулятор справляется в нештатной ситуации с поставленной задачей управления и имеет робастную БЗ, в основе проектирования которой лежат неробастные БЗ (см. рис. 9 и 11). В этом случае имеем новый синергетический эффект в теории искусственного интеллекта: из двух необученных классических автоматов можно спроектировать новый интеллектуальный квантовый автомат. Причем система управления на основе КНВ наследует лучшие характеристики качества управления от БЗ спроектированных ранее нечетких регуляторов, добавляя способность к самоорганизации в реальном времени.
 На основании изложенного можно сделать следующие выводы. Технология квантового нечеткого вывода, не разрушая нижний исполнительский уровень управления, обеспечивает систему дополнительным свойством робастности только за счет использования нового квантового программно-алгоритмического обеспечения. Проведенные эксперименты и результаты моделирования показали, что интеллектуальное управление позволяет в непредвиденных ситуациях управления гарантированно достигать цели управления с минимальным расходом ресурса, что по своей сути отражает на содержательном уровне само определение целенаправленной деятельности ИСУ. Продемонстрировано существование непредвиденных ситуаций управления, в которых НР не обладают требуемым качеством робастности, а квантовый нечеткий регулятор (на основе этих же НР) справляется с задачей управления на требуемом уровне качества управления. Установленный эффект подтверждает реализацию принципа самоорганизации БЗ за счет использования алгоритма КНВ. Показано применение квантовых вычис- лений на классическом процессоре в режиме реального времени. Результаты моделирования и экспериментов подтверждают полезность и эффективность использования скрытой квантовой информации, извлекаемой из классических состояний коэффициентов усиления, в процессах управления. Таким образом, показаны эффективность и необходимость применения квантовых вычислений и алгоритмов управления не только для квантовых систем, но и для классических ОУ.
На основании изложенного можно сделать следующие выводы. Технология квантового нечеткого вывода, не разрушая нижний исполнительский уровень управления, обеспечивает систему дополнительным свойством робастности только за счет использования нового квантового программно-алгоритмического обеспечения. Проведенные эксперименты и результаты моделирования показали, что интеллектуальное управление позволяет в непредвиденных ситуациях управления гарантированно достигать цели управления с минимальным расходом ресурса, что по своей сути отражает на содержательном уровне само определение целенаправленной деятельности ИСУ. Продемонстрировано существование непредвиденных ситуаций управления, в которых НР не обладают требуемым качеством робастности, а квантовый нечеткий регулятор (на основе этих же НР) справляется с задачей управления на требуемом уровне качества управления. Установленный эффект подтверждает реализацию принципа самоорганизации БЗ за счет использования алгоритма КНВ. Показано применение квантовых вычис- лений на классическом процессоре в режиме реального времени. Результаты моделирования и экспериментов подтверждают полезность и эффективность использования скрытой квантовой информации, извлекаемой из классических состояний коэффициентов усиления, в процессах управления. Таким образом, показаны эффективность и необходимость применения квантовых вычислений и алгоритмов управления не только для квантовых систем, но и для классических ОУ.
Литература
1. Ulyanov S.V., Litvintseva L.V. Design of self-organized intelligent control system based on quantum fuzzy inference: Intelligent system of systems engineering approach. Proc. of IEEE Internat. Conf. on System, Man and Cybernetics (SMC’2005), Hawai, USA, 2005, vol. 4.
2. Ulyanov S.V., Panfilov S.A., Kurawaki I., Yazenin A.V. Information analysis of quantum gates for simulation of quantum algorithms on classical computers, Proc. of Intern. Conf. QCM&C’2000. Capri, Italy, 2000, Kluwer Acad. Plenum Publ., 2001, pp. 207–214.
3. Решетников А.Г., Ульянов С.В. Метод извлечения знаний из физически измеряемого сигнала обучения: проектирование баз знаний нечеткого регулятора. Системный анализ в науке и образовании. 2013. Вып. 1.
4. Zurek W.H. Probabilities from entanglement, Born’s rule pk =|Yk|2 from envariance. Phys. Review, 2005, vol. A71, № 5.
5. Гольденблат И.И., Ульянов С.В. Введение в теорию относительности и ее приложения к новой технике. М.: Физматгиз, 1979.
6. Петров Б.Н., Уланов Г.М., Ульянов С.В. Проблемы управления релятивистскими и квантовыми динамическими системами. М.: Наука, 1982.
7. Li Y., Ang K.H., Chong G.C.Y. Patents, software and hardware for PID control: an overview and analysis of the current art. IEEE Control Syst. Mag., 2006, vol. 26, no. 1, pp. 42–54.
8. Решетников А.Г., Ульянов С.В., Шоланов К.С. Робастное интеллектуальное управление физическим динамически неустойчивым объектом «каретка–перевернутый маятник». Ч. 2: Технологии квантовых вычислений. Системный анализ в науке и образовании. 2013. Вып. 1. URL: http://sanse.ru/download/155 (дата обращения: 11.09.2013).
9. Khan H. PID controller: Comparative analysis and design diverse realizations (Moving towards efficient control in robotics and industries), Lambert Academic Publ. House, 2012.
10. Choi D., Oh J.-H. Human-friendly motion control of a wheeled inverted pendulum by reduced-order disturbance observer, IEEE Intern. Conf. on Robotics and Automation Pasadena, CA, USA, 2008, May 19–23, pp. 2521–2526.
11. Nawawi S.W., Ahmad M.N., and Osman J.H.S. Real-time control system for a two-wheeled inverted pendulum mobile – robot. Advanced Knowledge Application in Practice, InTech, 2010, pp. 299–312.
12. Gocmen A. Design of two wheeled electric vehicle. Master Sci. Thesis, Atilim Univ., 2011.
13. Moghaddas M., RezaDastranj M., Changizi N., and Khoori N. Design of Optimal PID Controller for Inverted Pendulum Using Genetic Algorithm. Intern. Journ. of Innovation, Management and Technology, 2012, vol. 3, no. 4.
14. Kumar P., Mehrotra O.N., Mahto J. Tuning of PID controller of inverted pendulum using genetic algorithm. Intern. Journ. of Research in Engineering and Technology, 2012, vol. 01, iss. 03.
References
1. Ulyanov S.V., Litvintseva L.V. Design of self-organized intelligent control system based on quantum fuzzy inference: Intelligent system of systems engineering approach. Proc. of IEEE int. conf. on system, man and cybernetics (SMC’2005). Hawai, USA, vol. 4.
2. Ulyanov S.V., Panfilov S.A., Kurawaki I., Yazenin A.V. Information analysis of quantum gates for simulation of quantum algorithms on classical computers. Proc. of int. conf. on quantum communication, measurements and computing (QCM&C’2000). Kluwer Acad. Plenum Publ., 2001, pp. 207–214.
3. Reshetnikov A.G., Ulyanov S.V. Knoledge extract method from physically measured teaching signal: knowledge base design for fuzzy controller. Sistemnyy analiz v nauke i obrazovanii [System analyze in sience and education]. 2013, vol. 1.
4. Zurek W.H. Probabilities from entanglement, Born’s rule pk =|Yk|2 from envariance. Phys. Review. 2005, vol. A71, no. 5.
5. Goldenblat I.I., Ulyanov S.V. Vvedenie v teoriyu otnositelnosti i ee prilozheniya k novoy tekhnike [Introdaction to relativity theory and its applications to a new technique]. Moscow, Fizmatgiz Publ., 1979.
6. Petrov B.N., Ulanov G.M., Ulyanov S.V. Problemy upravleniya relyativistskimi i kvantovymi dinamicheskimi sistemami [Control problems of relativistic and quantum dynamic systems]. Moscow, Nauka Publ., 1982.
7. Li Y., Ang K.H., Chong G.C.Y. Patents, software and hardware for PID control: an overview and analysis of the current art. IEEE Control Syst. Mag. 2006, vol. 26, no. 1, pp. 42–54.
8. Reshetnikov A.G., Ulyanov S.V., Sholanov K.S. Robust intelligent control of physical dynamic unstable object «cart – pole». Pt. 2: quantum computing technology. Sistemnyy analiz v nauke i obrazovanii [System analyze in sience and education]. 2013, vol. 1. Available at: http://sanse.ru/download/155 (accessed 11 September 2013).
9. Khan H. PID controller: Comparative analysis and design diverse realizations (Moving towards efficient control in robotics and industries). Lambert Academic Publ. House, 2012, 96 p.
10. Choi D., Oh J.-H. Human-friendly motion control of a wheeled inverted pendulum by reduced-orderdisturbance observer. IEEE int. conf. on robotics and automation Pasadena. CA, USA, 2008, pp. 2521–2526.
11. Nawawi S. W., Ahmad M. N., Osman J. H. S., Real-time control system for a two-wheeled inverted pendulum mobile – robot. Advanced knowledge application in practice. InTech, 2010, pp. 299–312.
12. Gocmen A. Design of two wheeled electric vehicle. Master Sci. thesis, Atilim Univ. Publ., 2011.
13. Moghaddas M., RezaDastranj M., Changizi N., Khoori N. Design of Optimal PID Controller for Inverted Pendulum Using Genetic Algorithm. Int. journ. of innovation, management and technology. 2012, vol. 3, no. 4.
14. Kumar P., Mehrotra O.N., Mahto J. Tuning of PID controller of inverted pendulum using genetic algorithm. Int. journ. of research in engineering and technology. 2012, vol. 01, iss. 03. Available at: http://ijret.org/volumes/2012_11_Vol_01_Iss_03/ P2012_01_03_029.pdf (accessed 10 August 2012).




 исунке 1 показана функциональная структура модели КНВ. На вход КНВ в реальном времени поступают сигналы управления от сфор- мированных заранее БЗ НР (шаг «Начальное состояние»). Следующим шагом является процесс нормализации полученных сигналов в интервале [0 1] путем деления амплитуд траектории сигналов управления на максимальные амплитуды. После нормировки сигналов осуществляется формирование квантовых битов из текущих значений нормированных сигналов управления. С этой целью предварительно определяется функция плотности распределения вероятности по представленным выборочным траекториям сигналов управления.
исунке 1 показана функциональная структура модели КНВ. На вход КНВ в реальном времени поступают сигналы управления от сфор- мированных заранее БЗ НР (шаг «Начальное состояние»). Следующим шагом является процесс нормализации полученных сигналов в интервале [0 1] путем деления амплитуд траектории сигналов управления на максимальные амплитуды. После нормировки сигналов осуществляется формирование квантовых битов из текущих значений нормированных сигналов управления. С этой целью предварительно определяется функция плотности распределения вероятности по представленным выборочным траекториям сигналов управления. =квантовый бит.
=квантовый бит. На рисунке 2 схематично отображены вычислительный процесс и формирование квантового бита для текущего состояния нормированного сигнала управления, описывающего коэффициенты усиления нечеткого ПИД-регулятора в структуре ИСУ.
На рисунке 2 схематично отображены вычислительный процесс и формирование квантового бита для текущего состояния нормированного сигнала управления, описывающего коэффициенты усиления нечеткого ПИД-регулятора в структуре ИСУ. На рисунке 4 приведен пример формирования пространственной корреляции в КНВ из сигналов управления коэффициентами усиления двух нечетких ПИД-регуляторов, БЗ которых спроектированы с помощью инструментария ОБЗ для двух различных ситуаций управления.
На рисунке 4 приведен пример формирования пространственной корреляции в КНВ из сигналов управления коэффициентами усиления двух нечетких ПИД-регуляторов, БЗ которых спроектированы с помощью инструментария ОБЗ для двух различных ситуаций управления.
 выглядит следующим образом:
выглядит следующим образом:
 – используемое значение сигналов управления пропорциональным коэффициентом усиления БЗ первого НР, спроектированного для первой фиксированной ситуации управления;
– используемое значение сигналов управления пропорциональным коэффициентом усиления БЗ первого НР, спроектированного для первой фиксированной ситуации управления;  – значение сигналов управления дифференциальным коэффициентом усиления БЗ второго НР, разработанного для второй ситуации управления (существенно отличающейся от первой по внешним условиям функционирования ОУ).
– значение сигналов управления дифференциальным коэффициентом усиления БЗ второго НР, разработанного для второй ситуации управления (существенно отличающейся от первой по внешним условиям функционирования ОУ). и аналогичные комбинации коэффициентов усиления. Как видно из обозначений, имеется 16 возможных состояний, описывающих комбинации корреляций (с учетом их типа и вида) между соответствующими коэффициентами усиления двух НР, спроектированных для разных ситуаций управления.
и аналогичные комбинации коэффициентов усиления. Как видно из обозначений, имеется 16 возможных состояний, описывающих комбинации корреляций (с учетом их типа и вида) между соответствующими коэффициентами усиления двух НР, спроектированных для разных ситуаций управления. С точки зрения квантовой теории информации чистое квантовое состояние характеризуется, как известно, нулевым значением энтропии фон Неймана. Следовательно, интеллектуальное квантовое состояние в рассматриваемом КА имеет место для минимума информационной энтропии квантового состояния Шеннона. Искомый минимум достигается, в свою очередь, при максимуме вероятности состояния (по определению информационной энтропии квантового состояния Шеннона
С точки зрения квантовой теории информации чистое квантовое состояние характеризуется, как известно, нулевым значением энтропии фон Неймана. Следовательно, интеллектуальное квантовое состояние в рассматриваемом КА имеет место для минимума информационной энтропии квантового состояния Шеннона. Искомый минимум достигается, в свою очередь, при максимуме вероятности состояния (по определению информационной энтропии квантового состояния Шеннона  , то есть глобальный минимум наблюдается при максимуме вероятности Pi). Так как Pi по определению есть квадрат соответствующей амплитуды вероятностей, принцип максимума амплитуды вероятностей при коррелированном состоянии может быть принят за критерий отбора приоритетного «интеллектуального» корреляционного (когерентного) состояния в суперпозиции возможных кандидатов [5, 6].
, то есть глобальный минимум наблюдается при максимуме вероятности Pi). Так как Pi по определению есть квадрат соответствующей амплитуды вероятностей, принцип максимума амплитуды вероятностей при коррелированном состоянии может быть принят за критерий отбора приоритетного «интеллектуального» корреляционного (когерентного) состояния в суперпозиции возможных кандидатов [5, 6]. Таким образом, вычислением амплитуд квантовых состояний в суперпозиции состояний со смешанными видами квантовой корреляции (рис. 1) и выбором среди них максимальной реализуется модель квантового оракула, обладающего (по определению понятия квантового оракула) необходимой информацией об искомом решении.
Таким образом, вычислением амплитуд квантовых состояний в суперпозиции состояний со смешанными видами квантовой корреляции (рис. 1) и выбором среди них максимальной реализуется модель квантового оракула, обладающего (по определению понятия квантового оракула) необходимой информацией об искомом решении. Для демонстрации возможностей технологии квантовых вычислений используем классическую задачу теории управления «каретка – перевернутый маятник». Одно из решений данной задачи – ПИД-регулятор в контуре обратной связи. Согласно [9–12], в качестве нижнего исполнительного уровня традиционный ПИД-регулятор и его модификации используются более чем в 85 % контуров управления в промышленных и непромышленных структурах САУ, включая объекты с повышенной социально-экономической ответственностью. Настройка и проектирование регулятора осуществляются как экспертом, так и различными программами. Обычно при проектировании используют интеллектуальные технологии, и этому посвящено множество работ, например [13, 14]. В основном в них рассматриваются создание и обучение нейронных сетей или БЗ с использованием различных алгоритмов обучения. В отличие от этих работ в данном эксперименте рассмотрим возможность применения КНВ для объединения БЗ, полученных на основе обучающего сигнала с физического объекта (ГА-ПИД-регулятор) и верифицированной математической модели [3] (рис. 5). В таблице 1 приведено сравнение БЗ, используемых для формирования КНВ.
Для демонстрации возможностей технологии квантовых вычислений используем классическую задачу теории управления «каретка – перевернутый маятник». Одно из решений данной задачи – ПИД-регулятор в контуре обратной связи. Согласно [9–12], в качестве нижнего исполнительного уровня традиционный ПИД-регулятор и его модификации используются более чем в 85 % контуров управления в промышленных и непромышленных структурах САУ, включая объекты с повышенной социально-экономической ответственностью. Настройка и проектирование регулятора осуществляются как экспертом, так и различными программами. Обычно при проектировании используют интеллектуальные технологии, и этому посвящено множество работ, например [13, 14]. В основном в них рассматриваются создание и обучение нейронных сетей или БЗ с использованием различных алгоритмов обучения. В отличие от этих работ в данном эксперименте рассмотрим возможность применения КНВ для объединения БЗ, полученных на основе обучающего сигнала с физического объекта (ГА-ПИД-регулятор) и верифицированной математической модели [3] (рис. 5). В таблице 1 приведено сравнение БЗ, используемых для формирования КНВ. Таким образом, имеем новый синергетический эффект за счет квантовой самоорганизации знаний: спроектированный на основе КНВ интел- лектуальный регулятор справляется в нештатной ситуации с поставленной задачей управления и имеет робастную БЗ, в основе проектирования которой лежат неробастные БЗ (см. рис. 9 и 11). В этом случае имеем новый синергетический эффект в теории искусственного интеллекта: из двух необученных классических автоматов можно спроектировать новый интеллектуальный квантовый автомат. Причем система управления на основе КНВ наследует лучшие характеристики качества управления от БЗ спроектированных ранее нечетких регуляторов, добавляя способность к самоорганизации в реальном времени.
Таким образом, имеем новый синергетический эффект за счет квантовой самоорганизации знаний: спроектированный на основе КНВ интел- лектуальный регулятор справляется в нештатной ситуации с поставленной задачей управления и имеет робастную БЗ, в основе проектирования которой лежат неробастные БЗ (см. рис. 9 и 11). В этом случае имеем новый синергетический эффект в теории искусственного интеллекта: из двух необученных классических автоматов можно спроектировать новый интеллектуальный квантовый автомат. Причем система управления на основе КНВ наследует лучшие характеристики качества управления от БЗ спроектированных ранее нечетких регуляторов, добавляя способность к самоорганизации в реальном времени. На основании изложенного можно сделать следующие выводы. Технология квантового нечеткого вывода, не разрушая нижний исполнительский уровень управления, обеспечивает систему дополнительным свойством робастности только за счет использования нового квантового программно-алгоритмического обеспечения. Проведенные эксперименты и результаты моделирования показали, что интеллектуальное управление позволяет в непредвиденных ситуациях управления гарантированно достигать цели управления с минимальным расходом ресурса, что по своей сути отражает на содержательном уровне само определение целенаправленной деятельности ИСУ. Продемонстрировано существование непредвиденных ситуаций управления, в которых НР не обладают требуемым качеством робастности, а квантовый нечеткий регулятор (на основе этих же НР) справляется с задачей управления на требуемом уровне качества управления. Установленный эффект подтверждает реализацию принципа самоорганизации БЗ за счет использования алгоритма КНВ. Показано применение квантовых вычис- лений на классическом процессоре в режиме реального времени. Результаты моделирования и экспериментов подтверждают полезность и эффективность использования скрытой квантовой информации, извлекаемой из классических состояний коэффициентов усиления, в процессах управления. Таким образом, показаны эффективность и необходимость применения квантовых вычислений и алгоритмов управления не только для квантовых систем, но и для классических ОУ.
На основании изложенного можно сделать следующие выводы. Технология квантового нечеткого вывода, не разрушая нижний исполнительский уровень управления, обеспечивает систему дополнительным свойством робастности только за счет использования нового квантового программно-алгоритмического обеспечения. Проведенные эксперименты и результаты моделирования показали, что интеллектуальное управление позволяет в непредвиденных ситуациях управления гарантированно достигать цели управления с минимальным расходом ресурса, что по своей сути отражает на содержательном уровне само определение целенаправленной деятельности ИСУ. Продемонстрировано существование непредвиденных ситуаций управления, в которых НР не обладают требуемым качеством робастности, а квантовый нечеткий регулятор (на основе этих же НР) справляется с задачей управления на требуемом уровне качества управления. Установленный эффект подтверждает реализацию принципа самоорганизации БЗ за счет использования алгоритма КНВ. Показано применение квантовых вычис- лений на классическом процессоре в режиме реального времени. Результаты моделирования и экспериментов подтверждают полезность и эффективность использования скрытой квантовой информации, извлекаемой из классических состояний коэффициентов усиления, в процессах управления. Таким образом, показаны эффективность и необходимость применения квантовых вычислений и алгоритмов управления не только для квантовых систем, но и для классических ОУ.