Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Автоматизированная система тестирования программных средств в скомпилированном виде
Аннотация:В статье отмечается, что обязательным условием широкого использования программных средств является сертификация, заключающаяся в их формальных испытаниях специалистами, гарантирующими соответствие программных средств стандартам и нормативным документам. Сертификация предусматривает контролируемое выполнение программы на конечном множестве наборов данных и анализ этого выполнения с целью обнаружения ошибок. На основе анализа показана необходимость тестирования программных средств в скомпилированном виде. В качестве аппарата для создания конечного множества наборов данных авторами предлагается использовать модифицированные генетические алгоритмы. Рассмотрена методика (топология) представления исходных данных при использовании программных средств для инженерных расчетов. Показано, что топологию можно свести к представлению в виде переменных трех типов: множества исходных данных вещественного случайного вида в определенном интервале, множества исходных данных целочисленного положительного вида в определенном интервале, множества логических (булевых) переменных. Предложен генотип кодирования топологии исходных данных в виде трех хромосом. Разработан алгоритм формирования конечного множества наборов данных, и обоснованы критерии их полноты. Описаны последовательность и методика тестирования программных средств. В качестве примера приведены продукционные модели, оценивающие результаты тестирования. Показано преимущество данной методики по сравнению с применяемыми в настоящее время способами сертификации программных средств в скомпилированном виде.
Abstract:The article states that the essential condition of an extensive software use is ISO/IEC 00002 certification. It in-volves formal testing by specialists to ensure its compliance with standards and regulations. Testing is to be ensured by a specified quality of the assigned tasks results. The article points out that certification provides controlled program running with a finite set of data and its further analy-sis in order to detect errors. The analysis proves relevance of the following problem: software has to be tested in a compiled form. The authors propose the modified genetic algorithms as a tool for creating a finite set of data. The article presents a meth-odology (topology) of the initial data (ID) representation using software tools for engineering calculations. The topology in question can be reduced to representation of three types of variables: ID sets of real random type within a certain range, ID sets of positive integer type within a certain range, sets of logical (Boolean) variables. The authors suggest the initial data to-pology coding genotype as three chromosomes. An algorithm of the finite data sets generation is developed, with the data completeness criteria being established. The sequence and technique of software testing is described. The procedure-oriented (production) models to evaluate test results are given as examples. The article shows the advantage of this method compared to the current means of certification of compiled software.
| Авторы: Палюх Б.В. (pboris@tstu.tver.ru) - Тверской государственный технический университет (профессор), г. Тверь, Россия, доктор технических наук, Семенов Н.А. (dmitrievtstu@mail.ru) - Тверской государственный технический университет (профессор кафедры «Информационные системы»), г. Тверь, Россия, доктор технических наук, Бурдо Г.Б. (gbtms@yandex.ru) - Тверской государственный технический университет (профессор, зав. кафедрой «Технология и автоматизация машиностроения»), г. Тверь, Россия, доктор технических наук, Мельникова В.В. (viklipse@mail.ru) - Тверской государственный технический университет, Тверь, Россия, Аспирант | |
| Ключевые слова: конечное множество наборов данных, продукционные модели, топология, генотип, тестирование и сертификация скомпилированных программных средств |
|
| Keywords: finite data set, procedure -oriented (production) models, topology, genotype, testing and certification of compiled software |
|
| Количество просмотров: 6194 |
Версия для печати Выпуск в формате PDF (7.83Мб) Скачать обложку в формате PDF (1.01Мб) |
Обязательным условием широкого использования программных средств (ПС) является сертификация, которая заключается в их формальных испытаниях специалистами, гарантирующими соответствие стандартам и нормативным документам, в частности стандарту ISO/IEC 00002. При этом в испытаниях должно обеспечиваться заданное качество результатов решения предписанных задач. Сертификация ПС, принятая в России, предусматривает проведение их тестирования, то есть контролируемое выполнение программы на конечном множестве наборов данных (КМНД) и анализ этого выполнения с целью обнаружения ошибок. Становится понятным, что рациональное ограничение КМНД во многом предопределяет трудоемкость и корректность тестирования, причем неавтоматизированное определение КМНД приводит к дополнительным трудозатратам. Таким образом, задача формирования оптимального КМНД является актуальной. Постановка задачи Известны способы тестирования ПС на основе использования генетических алгоритмов (ГА) [1–3]. Критериями полноты тестового покрытия обычно являются количество покрытых операторов в исходном коде, покрытых ветвей в графе потока управления, покрытых путей графа потока управления. Однако проверка возможна при наличии исходных текстов программ, в то время как государственные органы сертификации работают со скомпилированными ПС. Поэтому логичной является постановка задачи создания автоматизированной системы формирования рационального КМНД для тестирования скомпилированных ПС. В качестве аппарата для создания КМНД авторы предлагают модифицированные ГА. Методика представления (топология) исходных данных В основу создания КМНД для контролируемых расчетов положен анализ структуры и параметров исходных данных (ИД), используемых в ПС при выполнении. Их предлагаемое представление позволит при сертификации ПС смоделировать тестирование с использованием исходных текстов программ. Топология ИД была рассмотрена и представлена в виде следующих типов переменных. 1-й тип. Множества ИД вещественного случайного вида, Bº{Bк}, Bk={bкr}, где bкr – случайное значение входной переменной Bk; Множество 2-й тип. Множества ИД целочисленного положительного вида, Aº{Ai}, Ai={aij}, где n – число целочисленных переменных; t – число значений Ai-й переменной; В отличие от данных 1-го типа, используемых непосредственно для получения численного значения результата при использовании ПС, данные 2-го типа используются для определения основного пути графа вычислений. К этим же данным, естественно, относятся и ИД символьного типа (буквы, слова, фразы) из определенного ограниченного набора. Это корректно, так как с точки зрения влияния на ход выполнения программы они являются переменными одного смыслового содержания. 3-й тип. Множества логических (булевых) переменных в составе ИД, L={Lq}, Исходные данные 3-го типа определяют разветвление пути графа вычислений. По смыслу им соответствуют и синтаксические переменные, состоящие из наборов по две буквы (слова, фразы). Методика и алгоритм создания КМНД Предлагаемая методика состоит в том, чтобы при тестировании скомпилированных программ смоделировать такой вычислительный процесс, который косвенно отражал бы процесс и критерии тестирования ПС в исходных текстах. Такие критерии, как количество покрытых ветвей и путей в графе потока управления, косвенно определяются числом переборов ИД переменных из типов 2 и 3. Корректность работы программы в диапазоне возможных числовых значений исходных данных, используемых для непосредственных расчетов, определяется тем, насколько и с какой дискретностью перекрыта область значений переменных 1-го типа. Рассмотрим генотип кодирования ИД для тестирования. Топологию исходных данных удобнее представлять в виде генотипа, состоящего из трех хромосом, каждая из которых отвечает за ИД соответствующего типа. Структура хромосом показана на рисунке 1.
Алгоритм создания КМНД построен следующим образом. На первом этапе создаются наборы для обеспечения тестового покрытия ветвей и путей в графе потока информации, то есть они варьируют хромосомами типов 2 и 3 при фиксированном значении хромосомы 1. Учитывая, что не видно места ветвления программы, для полного тестового покрытия необходима стопроцентная генерация возможных вариантов. Однако на практике бывает достаточно ограничить перебор, задав для формирования КМНД процент перебора данных в переменных целочисленного 2-го типа и обеспечив полный перебор данных 3-го булева типа. Очевидно, что, допуская определенное число повторов конкретного значения переменной Ai при формировании КМНД и зная закон ее распределения, можно варьировать числом пройденных потоков управления. Исходная популяция хромосом для первого этапа (наборы I и II) получается следующим образом. Значение каждой величины Bk случайным образом генерируется из срединного интервала (рекомендуется 7–11 интервалов, IN). Из хромосомы 1 со значениями Bk из срединного интервала Iср, хромосом 2 и 3 со случайными значениями {akj} и {lqr} (рис. 2) получается первый набор из трех хромосом. Следующий, II набор из 3 хромосом получается таким образом: а) первая и вторая хромосомы остаются неизменными; б) в третьей хромосоме гены l¢qr дополняют гены lqr до полного множества {lqr}=Lq (то есть берется второй элемент бинарного множества): l¢qr=Lq\lqr. Третий и последующие (производные) наборы хромосом на первом этапе строятся по следующему алгоритму. 1-й шаг. Из исходной популяции хромосом берется набор I. 2-й шаг. Указанный набор фиксируется в новом производном наборе хромосом. 3-й шаг. В хромосоме 2 производного набора случайным образом мутируется n-й ген (не допуская повторов с предыдущими вариантами), получается новый тестовый набор, который заносится в память. 4-й шаг. В полученном на шаге 3 тестовом наборе хромосома 3 заменяется хромосомой из исходного набора II. Тестовый набор заносится в память. 5-й шаг. Проверяется условие окончания мутации гена n (по проценту покрытия значений интервала от 6-й шаг. Проверяется условие окончания мутации предшествующего (n–1) гена. Если нет, то переход к оператору 7, иначе – шаг 8. 7-й шаг. В последнем тестовом наборе случайным образом, исключая повторы, в хромосоме 2 мутируется предшествующий (n–1) ген. Переход на шаг 3. 8-й шаг. Проверяется условие окончания мутации предшествующего (n–2) гена. Если нет, то переход к оператору 9, иначе – шаг 10. 9-й шаг. В последнем тестовом наборе случайным образом, исключая повторы, в хромосоме 2 мутируется предшествующий (n–2) ген. Переход на шаг 3. 10-й шаг. Проверяется условие окончания мутации (n–3) гена. Если нет, то переход к шагу 11, иначе – шаг 12. 11-й шаг. В последнем тестовом наборе случайным образом, исключая повторы, в хромосоме 2 мутируется (n–3) ген. Переход на шаг 3. (и т.д.)
Последний шаг. В тестовом наборе случайным образом мутируется (n–(n–1)) ген. Переход на шаг 3. Отдельно следует остановиться на процентном соотношении мутируемых вариантов генов во второй хромосоме. Для гена A1, очевидно, должен быть обеспечен полный перебор, то есть проверены все значения из интервала [a11, a1,t1] (рис. 3). Для гена A2, чтобы только пройти все ребра в потоке управления, достаточным будет обеспечение проверки (для каждого значения гена A1) для Применив формулу в виде В общем случае для двух соседних генов
где ti – количество значений вариантов гена Ai (предыдущего); ti+1 – количество значений вариантов гена Ai+1 (последующего). Очевидно, что коэффициент Ki определяет часть возможных значений (часть поля рассеивания) гена Ai+1, следовательно, зная закон рассеивания значений гена Ai+1, можно определить процент перекрытия графов потоков управления из двух смежных ребер Pi, i+1 для каждого значения гена Ai. Поэтому в общем случае процент перекрытия всех возможных потоков управления будет P1= =P1,2´P2,3´ …´Pi,i+1´ …´Pn–1, n, где i – номер переменной гена Ai; n – количество переменных.
На втором этапе формируется КМНД для тестирования ПС с точки зрения выполнения корректности расчетов в области существования переменных, определяющих числовые данные вычислений. С этой целью строятся варианты наборов из мутируемой хромосомы 1 и постоянного состава генов во второй и третьей хромосомах из набора I первого этапа. Исходная популяция хромосом состоит из двух наборов, определяемых первой хромосомой. В первом наборе в хромосоме присутствуют максимальные значения Bk, во втором – минимальные (рис. 4). Остальные тестовые наборы получаются мутацией первой хромосомы исходя из того, что диапазоны каждого гена Bk разбиты на INk число интервалов. Варьируя числом интервалов INk, на которое разбивается диапазон всех значений переменных Bk, можно управлять количеством наборов хромосом, получаемых на этом этапе. Предельное количество интервалов INk max определяется исходя из ограниченного практическими (экспертными) соображениями дискретности DBk переменной Bk:
Эти факторы определяют условия окончания мутации гена Bk. Таким образом, алгоритм формирования КМНД на втором этапе следующий. Шаг 1. Формируем исходную популяцию хромосом (рис. 3). Шаг 2. Берем из исходной популяции хромосом набор I. Шаг 3. В наборе I выполняем случайным образом неповторяющуюся мутацию в гене Bm первой хромосомы (в пределах срединного и в каждом смежном интервале). Запоминаем тестовый набор. Шаг 4. Определяем окончание мутации гена Bm (по одному значению в срединном и в каждом смежном интервале). Если да – переход к шагу 5, нет – возврат к шагу 3. Шаг 5. Проверяем окончание мутации Bm-1 гена аналогично гену Bm. Если нет – переход на шаг 6, если да – переход на шаг 7. Шаг 6. Случайным образом выполняем мутацию гена Bm–1 (аналогично Bm). Возврат на шаг 3. Шаг 7. Проверяем окончание мутации в гене Bm–2. Если нет – переход на шаг 8, если да – переход на шаг 9 и т.д. Предпоследний шаг. Проверяем окончание мутации по Bm–(m–1) гену. Если да – окончание генерации тестовых наборов, нет – переход к последнему шагу. Последний шаг. Случайным образом (аналогично гену Bm) мутируется Bm–(m–1) ген. Возврат на шаг 3. Множества ИД вещественного случайного вида, Bº{Bk}, Объединяя множество наборов, полученных на первом–третьем этапах, получаем конечное множество наборов данных для тестирования. Методика тестирования ПС На этапе тестирования сначала экспертным путем устанавливается параметр Ki и тем самым определяется число автоматически генерируемых вариантов в КМНД. Процесс тестирования состоит в следующем. Первоначально тестируются ПС с использованием КМНД, полученных на первом этапе (КМНД1), то есть делается попытка подтверить как минимум корректность ветвей и путей в графе потока информации. Продукционными моделями знаний делается заключение Z1 о результате тестирования с помощью КМНД1, Z1 имеет три нечетких значения: хороший, удовлетворительный, неудовлетворительный. При этом анализируются полнота КМНД1 (сравнением с максимально возможным исходя из принятого значения коэффициента Ki и количества вариантов t1 гена A1, и вероятностей Pi, i+1 и P1) и адекватность полученных результатов. Полнота оценивается нечеткой переменной α1, имеющей три значения: достаточный, возможный, недостаточный. Адекватность результатов расчетов оценивается нечеткой переменной β1, имеющей три значения: адекватный, допустимый, неадекватный. Продукционные модели, оценивающие тестирование, построены по виду ЕСЛИ (α1=<значение> И β1=<значение>), ТО Z1=<значение>. Во вторую очередь тестируются ПС с использованием КМНД2 и КМНД3, полученных на втором и третьем этапах, что является попыткой определить корректность выполнения расчетов на всем диапазоне возможных значений входных данных. Продукционными моделями знаний делается заключение Z2 о результате тестирования с помощью КМНД2 и КМНД3. Z2 тоже имеет три нечетких значения: хороший, удовлетворительный, неудовлетворительный. При этом анализируются полнота КМНД2 (сравнением с максимально возможным исходя из максимального INmax числа интервалов вероятностей Pk и P2) и адекватность полученных результатов. Полнота и здесь оценивается нечеткой переменной α2, имеющей три значения: достаточный, возможный, недостаточный. Адекватность расчетов оценивается нечеткой переменной β2, имеющей три значения: адекватный, допустимый, неадекватный. Продукционные модели приобретают вид ЕСЛИ (α2=<значение> И β2=<значение>), ТО Z2=<значение>. Результирующее заключение Z, имеющее два значения – тестирование пройдено или тестирование не пройдено, – формируется продукционными моделями, построенными по виду ЕСЛИ (Z1=<значение> И = Z2<значение>), ТО Z=<значение>. Продукционные модели созданы на основе экспертных оценок. С целью увеличения степени достоверности результатов экспертным путем для нечетких переменных α1, α2 и β2, β2 разработаны числовые относительные шкалы (сравнением с максимально возможным набором данных для α1 и α2 и исходя из соотношения адекватных, сом- нительных и неадекватных результатов расчетов для β2 и β2). В заключение отметим, что в соответствии с предложенной методикой были разработаны программные средства для автоматизированного формирования КМНД и последующего тестирования программ. Справедливость изложенных положений была подтверждена сравнением тестирования ПС в скомпилированном виде с тестированием программ в исходных текстах. При пробных тестированиях сгенерированные наборы данных обеспечивали необходимую полноту тестового покрытия и значительно сокращали трудоемкость тестирования по сравнению с используемыми традиционными способами. Литература 1. Мельникова В.В., Палюх Б.В., Котов С.Л., Проскуряков М.А. Тестирование программ с использованием генетических алгоритмов // Программные продукты и системы. 2011. № 4. С. 114–117. 2. Котляров В.П., Коликова Т.В. Основы современного тестирования программного обеспечения, разработанного на С#: учеб. пособие. СПб, 2004. С. 55–57. 3. Котов С.В., Демирский А.А., Мельникова В.В. Проведение сертификационных испытаний часто обновляющихся ПС с использованием автоматизированной тестовой базы // Вестн. ВНИИМАШ, 2010. References 1. Melnikova V.V., Palyukh B.V., Kotov S.L., Proskuryakov M.A. Software testing using genetic algorithms. Programmnyie produkty i sistemy [Software & Systems]. Tver, 2011, no. 4, pp. 114–117 (in Russ.). 2. Kotlyarov V.P., Kolikova T.V. Osnovy sovremennogo testirovaniya programmnogo obespecheniya, razrabotannogo na C# [The basics of modern software testing developed with C#]. Study guide, St. Peterburg, 2004, pp. 55–57 (in Russ.). 3. Kotov S.V., Demirskiy A.A., Melnikova V.V. Sertification testing of frequently upgraded software using avtomated testing base. Vestnik VNIIMASh [The bulletin of the Russian Sci. Research Institute on Standardization and Certification in Machine Building], 2010 (in Russ.). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3770 |
Версия для печати Выпуск в формате PDF (7.83Мб) Скачать обложку в формате PDF (1.01Мб) |
| Статья опубликована в выпуске журнала № 1 за 2014 год. [ на стр. 123-128 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 , принимающие случайные значения в определенном интервале:
, принимающие случайные значения в определенном интервале: ,
,  ,
, ,
, – минимальное и максимальное значения входной переменной Bk; m – их количество.
– минимальное и максимальное значения входной переменной Bk; m – их количество.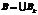 – это все массивы ИД случайного типа, определяющие их возможные наборы. Данные 1-го типа в основном подчиняются закону нормального распределения.
– это все массивы ИД случайного типа, определяющие их возможные наборы. Данные 1-го типа в основном подчиняются закону нормального распределения. :
: ,
, 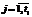 , aij–int,
, aij–int, и
и  – минимальное и максимальное значения Ai-й переменной.
– минимальное и максимальное значения Ai-й переменной. , d – их количество; Lq={lqr}, r=1, 2,
, d – их количество; Lq={lqr}, r=1, 2,  .
. Генами хромосомы являются переменные Ai, Bk, Lq.
Генами хромосомы являются переменные Ai, Bk, Lq.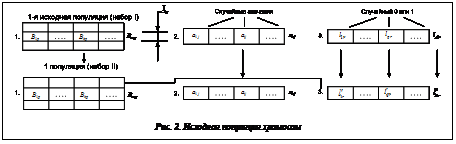 Предпоследний шаг. Проверяется окончание мутации (n–(n–1)) гена. Если нет, то переход к последнему шагу, иначе – окончание генерации тестовых наборов.
Предпоследний шаг. Проверяется окончание мутации (n–(n–1)) гена. Если нет, то переход к последнему шагу, иначе – окончание генерации тестовых наборов. его значений вариантов, где t1 – количество значений вариантов гена A1; t2 – количество значений вариантов гена A2.
его значений вариантов, где t1 – количество значений вариантов гена A1; t2 – количество значений вариантов гена A2. , можно управлять количеством сочетаний вариантов из двух ребер, то есть числом графов в потоке управления, состоящих из двух ребер. Коэффициент K1 берется в частях от t1 с округлением до большего целого. Скажем,
, можно управлять количеством сочетаний вариантов из двух ребер, то есть числом графов в потоке управления, состоящих из двух ребер. Коэффициент K1 берется в частях от t1 с округлением до большего целого. Скажем,  будет соответствовать перебор половины значений гена A2 для каждого значения гена A1, а K1=1 – перебор всех значений гена A2 для каждого значения гена A1, то есть перебор всех возможных графов потоков управления из двух первых ребер.
будет соответствовать перебор половины значений гена A2 для каждого значения гена A1, а K1=1 – перебор всех значений гена A2 для каждого значения гена A1, то есть перебор всех возможных графов потоков управления из двух первых ребер.
 Варьируя значением коэффициента Ki, можно изменять количество наборов хромосом, генерируемых на первом этапе. Поэтому, управляя значением Ki, можно находить и количество элементов в КМНД, определяющих возможные границы от перебора только ребер (
Варьируя значением коэффициента Ki, можно изменять количество наборов хромосом, генерируемых на первом этапе. Поэтому, управляя значением Ki, можно находить и количество элементов в КМНД, определяющих возможные границы от перебора только ребер ( ) до перебора всех графов в потоке управления из двух ребер (Ki=1). Следовательно, значением величины Ki определяется условие окончания генерации КМНД на первом этапе.
) до перебора всех графов в потоке управления из двух ребер (Ki=1). Следовательно, значением величины Ki определяется условие окончания генерации КМНД на первом этапе.
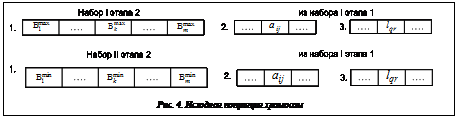 Определив на основе экспертных оценок закон распределения каждой переменной и учитывая рациональную величину DBk и процентное количество Rk проверяемых интервалов INk пров=INk´Rk (их расположение симметрично относительно срединного), можно управлять вероятностью Pk проверки возможных значений переменных Bk, а следовательно, и вероятностью P2 перебора графов потоков управления:
Определив на основе экспертных оценок закон распределения каждой переменной и учитывая рациональную величину DBk и процентное количество Rk проверяемых интервалов INk пров=INk´Rk (их расположение симметрично относительно срединного), можно управлять вероятностью Pk проверки возможных значений переменных Bk, а следовательно, и вероятностью P2 перебора графов потоков управления: 
 необходимо проверить на наличие так называемых критических значений. Таковыми являются минимальные и максимальные, а также нулевые значения, если значение какой-либо переменной меняет знак. Минимальные и максимальные значения переменных уже были учтены при формировании хромосом на втором этапе, поэтому следует дополнительно учесть лишь нулевые точки. С этой целью на третьем этапе в исходной популяции хромосом первого этапа (рис. 2) вместо множества срединных значений {Bk} вводятся нулевые значения для тех исходных данных, которые меняют знак.
необходимо проверить на наличие так называемых критических значений. Таковыми являются минимальные и максимальные, а также нулевые значения, если значение какой-либо переменной меняет знак. Минимальные и максимальные значения переменных уже были учтены при формировании хромосом на втором этапе, поэтому следует дополнительно учесть лишь нулевые точки. С этой целью на третьем этапе в исходной популяции хромосом первого этапа (рис. 2) вместо множества срединных значений {Bk} вводятся нулевые значения для тех исходных данных, которые меняют знак.