Трудно назвать какую-либо область деятельности, где не происходило бы накопление данных: банки сохраняют информацию о своих клиентах и их вкладах, магазины хранят данные о покупках, социальные сети – о запросах пользователей сети, их высказываниях, на промышленных предприятиях записываются параметры технологических процессов, медики хранят данные пациентов.
Создаваемые БД содержат полезную информацию, которая с успехом может использоваться для улучшения эффективности деятельности в той области, где эти данные собраны.
По этой причине все большую популярность приобретают различные алгоритмы, получившие общее название Data Mining, что буквально можно перевести как «раскопки данных». Пионерами Data Mining можно назвать Лафонтена и Маяковского. Первый в басне, известной нам в переводе Крылова, писал: «Навозну кучу разгребая, петух нашел жемчужное зерно». Маяковский прямо говорил о текстах: «Изводишь единого слова ради тысячи тонн словесной руды». В обоих случаях подчеркиваются суть и сложность алгоритмов этого класса: данных много, в них есть ценная информация, найти и извлечь ее непросто.
Технический термин Data Mining введен Григорием Пятецким-Шапиро в 1989 году. Другое часто используемое название для этих алгоритмов – Knowledge Data Discovery, или KDD, что можно перевести как «извлечение (обнаружение) знаний из данных». Как это всегда бывает с модным направлением исследований, сегодня под алгоритмами Data Mining понимают самый широкий класс алго- ритмов, от давно известных алгоритмов математической статистики, алгоритмов, применяемых в области ИИ (искусственного интеллекта), до алгоритмов, созданных специально для раскопки данных.
В данной статье рассматривается алгоритм, характерный именно для Data Mining. Он позволяет извлекать из БД ассоциативные правила. Впервые такой алгоритм, получивший название Apriori, был предложен в работе [1]. Рассмотрим эффективную модификацию этого алгоритма, основанную на шкалах, и его применение к задачам медицинской диагностики. Существует достаточно много реализаций алгоритма Apriori. Описание некоторых из них можно найти в работах [2–5]. Большинство из них ориентировано на анализ потребительских корзин.
Постановка задачи. Рассмотрим БД db, содержащую множество объектов:
db = {v1, v2, ..., vN}. (1)
Каждый объект vk БД характеризуется некоторым набором свойств Pk:
Pk = {pk1, pk2, ..., pkm}. (2)
Наборы Pk являются подмножествами общего для всех объектов множества свойств Properties:
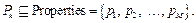 (3)
(3)
Будем полагать, что все свойства объектов являются бинарными, то есть объект vk может либо обладать, либо не обладать свойством pj. Позже бу- дет показано, как можно ослабить это ограничение для случая количественных показателей.
Поскольку в дальнейшем предметом исследований будут не сами объекты, а только их свойства, введем в рассмотрение БД dbp, содержащую только конкретные свойства объектов:
dbp = {P1, P2, ..., PN}. (4)
Пусть X – некоторый набор свойств:
X={pi1, pi2, ..., piq}. (5)
Частоту набора или его поддержку в базе dbp будем определять как долю тех наборов БД, которые содержат набор X:
 . (6)
. (6)
Ассоциативным правилом Rule будем называть правило вида
X®Y. (7)
Здесь X и Y – непересекающиеся наборы свойств:
 . (8)
. (8)
Важной характеристикой правила является его частота (support), которая определяется следующим образом:
 (9)
(9)
Правило Rule следует рассматривать как импликацию, правило вида «если, то». Если в некотором наборе имеет место X, то в нем имеет место и Y. Другими словами, появление X влечет появление Y. Чтобы правило имело практическую ценность, оно должно обладать высокой степенью достоверности.
Достоверность, или качество (confidence), является второй важнейшей характеристикой правила, которая определяется как доля всех наборов БД, содержащих X и Y, среди тех наборов, которые содержат X:
 (10)
(10)
Нетрудно заметить, что качество правила можно выразить через функцию поддержки Support:
 (11)
(11)
Цель алгоритма Apriori: найти все ассоциативные правила, у которых частота и качество выше заданных минимальных значений.
 (12)
(12)
Основная идея алгоритма Apriori. Идея, предложенная еще в работе [1], позволяет избавиться от полного перебора всех возможных наборов при по- строении ассоциативных правил. Суть идеи такова. Назовем набор свойств X частым, если Support(X) > > support_min. Справедливо следующее утверждение: если X – частый набор, то и все его подмножества являются частыми наборами.
Более важным является утверждение, следующее из отрицания этой импликации: если X не является частым набором, то и все его надмножества не являются частыми наборами.
Это свойство наборов, называемое антимонотонностью, при построении правил позволяет исключить из рассмотрения большое число наборов. Так, например, обнаружив, что некоторое свойство p редко появляется в наборах БД, можно не рассматривать все наборы БД, содержащие p.
Отсюда следует и общая схема реализации алгоритма Apriori. Вначале строится множество частых наборов F, содержащее наборы длины 1, и множество правил R, где посылка и заключение содержат наборы из F. Затем в цикле на основе уже построенных множеств частых наборов F и R длины k строятся множества F и R длины k+1. Цикл завершается, когда вновь создаваемое множество F длины k+1 пусто, то есть не существует частых наборов длины k+1.
Эту схему будем использовать и в нашем алгоритме AprioriScale, где рассмотрим ее более детально.
Алгоритм AprioriScale. Основные идеи
В основе модификации классического алгоритма AprioriScale лежат две основные идеи: первая связана со способом представления данных, вторая носит более фундаментальный характер и связана со способом построения достоверных правил.
Представление данных в алгоритме AprioriScale. Как представлять записи БД, которые описывают свойства, характеризующие запись? Естественный способ состоит в том, чтобы каждую запись рассматривать как переменную типа List. В этом случае запись БД представляет собой список, число элементов которого задает число свойств, которыми этот элемент обладает, а каждый элемент списка задает описание соответствующего свойства.
Такое представление хорошо тем, что сохраняет содержательный смысл свойств, а это крайне важно в прикладных задачах, когда пользователями программной системы являются специалисты в соответствующей прикладной области. Недостатками являются достаточно большой объем памяти, необходимый для хранения данных, и сложность обработки текстовых данных в сравнении с числовым представлением.
Оценим при таком способе представления данных сложность функции Support(X), лежащей в ос- нове всех вычислений. При расчете поддержки набора X необходимо в цикле по числу записей в БД определять, содержится ли список свойств набора X в списке, характеризующем k-ю запись Pk БД. Проверка вхождения данных одного списка в другой список требует O(M2) достаточно трудоемких операций, когда данными являются строки текста. Общая сложность функции Support представима как O(N * M2), где N – число записей в БД, а M – число свойств.
Можно ускорить вычисления этой функции, сохраняя тот же порядок сложности, но уменьшив константу, если перейти от текстов к числовому представлению данных List, учитывая бинарный характер свойств. В этом случае каждая запись БД будет представляться набором из m чисел, значение которых равно 1, если свойство присутствует в записи, и 0 в противном случае. Недостатком такого подхода является то, что труднее обеспечить содержательный смысл данных, представленных числами.
В алгоритме AprioriScale авторы постарались избежать указанных трудностей. С этой целью для представления свойств объектов выбран тип Enumeration (Перечисление). Особенностью этого типа является то, что внутреннее представление данных задается целыми числами, на которые отображаются элементы перечисления. Внешним представлением данных, с которым работает пользователь, остаются строки текста, описывающие свойства объектов.
Более того, для представления данных выбран не просто тип Enumeration, а специальный вид этого типа, называемый шкалой. Шкала характеризуется тем, что k-й элемент перечисления отображается в число 2k. Такое представление позволяет для множества из M свойств установить взаимно однозначное соответствие между всевозможными наборами свойств и целыми числами из диапазона [0–2M+1–1]. Таким образом, каждый элемент БД, задающий набор свойств, представляется одним целым числом. В двоичном представлении это- го числа единица в k-м разряде означает, что соответствующий объект обладает k-м свойством в перечислении. Подробности работы со шкалами даны в [6].
Представление данных перечислением, заданным шкалой, имеет еще одну немаловажную полезную особенность. Над элементами перечисления определены логические побитовые операции. Это позволяет крайне эффективно решать базовую для алгоритма операцию – определение вхождения элементов одного множества в другое. Пусть X – заданный набор свойств, а Pk – элемент БД. Объекты X и Pk принадлежат типу Enumeration, заданному шкалой. Тогда для установления того, что XÍPk, достаточно вычислить следующее булевское выражение:
(X & Pk) = X, (13)
где & – побитовая конъюнкция, выполняемая над двоичными представлениями X и Pk.
Будем также использовать знак операции | для логической побитовой операции дизъюнкции. Операции & и | можно рассматривать как операции пересечения и объединения соответствующих множеств.
Выбранное представление позволяет сложную операцию определения вхождения множества X в множество Y выполнять за константное время, не зависящее от размера множеств, практически мгновенно, поскольку для выполнения требуются две машинные операции компьютера. Отсюда существенно упрощается сложность вычисления функции Support. При выбранном представлении сложность вычисления этой функции O(N) линейно зависит от размера БД с минимальной константой.
Итеративный расчет достоверных ассоциативных правил. Уже отмечалось, что основная идея алгоритма Apriori связана с итеративной схемой построения частых наборов. Частые наборы длины k строятся на основе частых наборов длины k–1 и единичных частых наборов. Нечастые наборы в построении не участвуют. В этом суть алгоритма Apriori.
Предлагаемая в алгоритме Apriori схема построения правил такова. Пусть уже построены правила и частые наборы длины k–1. Тогда для построения правил на следующем шаге вначале строится множество частых наборов длины k. Элементы этого множества выбираются в качестве посылки (заключения) вновь строящихся правил. В качестве заключения (посылки) такого правила используются частые наборы длины от 1 до k. Такая схема требует хранения всех частых наборов любой длины и достаточно затратна как по памяти, так и по сложности вычислений.
В алгоритме AprioriScale, помимо свойства антимонотонности, характеризующего частые наборы, используется похожее свойство, характеризующее достоверные правила. Это свойство позволяет строить достоверные правила на шаге k на основании достоверных правил, построенных на шаге k–1. В основе алгоритма лежит следующее утверждение: если X ÞYk – достоверное правило, то и любое правило XÞYj, где Yj – собственное подмножество Yk , является достоверным.
Докажем справедливость этого утверждения.
Так как Yj – подмножество Yk, Yk можно представить в виде Yk =Yj | add. Эта запись учитывает, что переменные заданы перечислением, так что, объединение множеств выражается через операцию дизъюнкции.
Достоверность правила XÞYk вычисляется следующим образом:
 (14)
(14)
Достоверность правила XÞYj вычисляется как
 (15)
(15)
Знаменатели в формулах (14) и (15) совпадают, а числитель в формуле (14) по свойству часто- ты множеств меньше или равен числителю в формуле (15). Отсюда следует справедливость утверждения.
Следствие. Важнее не само утверждение, а его отрицание. И здесь имеет место антимонотонность. Если правило XÞYj недостоверно, то недостоверно и правило XÞYk. Отсюда следует, что достоверные правила с заданной посылкой X можно строить на основе ранее построенных достоверных правил с той же посылкой.
Заметим, что утверждение касается только правил с заданной посылкой. Возможна ситуация, когда правила XÞY и Z ÞY недостоверны, а правило X | ZÞY достоверно. Поэтому недостаточно построить достоверные правила на шаге k, используя только достоверные правила шага k–1. К этому множеству правил достаточно добавить достоверные правила, посылка которых выбирается из множества частых правил длины k, а заключение является частым единичным набором.
Отсюда следует схема алгоритма AprioriScale. Вначале строится множество частых достоверных правил с единичной посылкой и заключением. Далее итеративно уже построенное множество достоверных частых правил на шаге k–1 расширяется. Затем к этому множеству добавляются достоверные правила, посылка которых выбирается из множества частых правил длины k, а заключение является частым единичным набором. Процесс продолжается, пока можно строить новые правила.
Рассмотрим, как происходит расширение множества достоверных правил на каждом шаге.
Пусть на шаге k–1 построено частое достоверное правило: X Þ Y.
Пусть cand – частый единичный набор. Тогда данное правило позволяет породить четыре правила:
X | candÞY, Y Þ X | cand,
X ÞY | cand, Y | cand Þ X.
Заметим, все четыре правила имеют одинаковую поддержку – Support(X | Y | cand). Так что, если значение поддержки меньше минимального значения, то ни один из четырех кандидатов не включается в список правил следующего шага. Для подсчета достоверности правил достаточно вычислить два значения функции Support – Support(X | cand) и Support(Y | cand).
Теорема. Алгоритм AprioriScale строит все частые достоверные правила.
Доказательство этого утверждения по сути приведено выше.
Подводя промежуточные итоги, отметим, что алгоритм AprioriScale позволяет
- существенно упростить и сократить объем БД; БД из N записей может быть представлена фай- лом из N целых чисел;
- для пользователя программы сохраняется естественное для данной проблемной области описание свойств рассматриваемых объектов;
- вычисление базисной для алгоритма функции Support может быть выполнено за линейное время, пропорциональное размеру БД и не зависящее от числа исследуемых свойств;
- в отличие от классического алгоритма Apriori, учитывающего только свойство антимонотонности частых множеств, в алгоритме учитывается свойство антимонотонности достоверных правил, позволяющее строить достоверные правила на основе ранее построенных достоверных правил меньшего размера.
Ограничения алгоритма и их преодоление
Рассмотрим ограничения, присущие алгоритму AprioriScale, и возможные способы их преодоления.
Количественные свойства. В алгоритме AprioriScale предполагается, что все свойства носят бинарный характер: свойство либо наличествует у объекта, либо нет. В то же время на практике свойство может быть представлено числом из некоторого диапазона. Подтверждений тому можно привести сколь угодно много, например, температура или давление, измеряемое у пациента, цена товара, длина запроса. Как поступать в таких случаях?
Нужно понимать, что ассоциативные правила носят качественный, а не количественный характер. Поэтому, как правило, точные значения из- меряемых параметров не столь важны. В боль- шинстве ситуаций достаточно разбить диапазон возможных значений параметра на несколько непересекающихся интервалов, обычно не более пяти. Например, при разбиении на три интервала каждому интервалу можно поставить в соответствие три свойства: норма, ниже нормы, выше нормы. В этом случае каждый количественный параметр заменяется k бинарными свойствами, где k – это число разбиений диапазона возможных значений исходного параметра. Следует заметить, что свойства «норма» или «ниже нормы» носят качественный характер и для ассоциативных правил более важны, чем знание количественных значений.
Так, для педиатрии большинство измеряемых параметров зависят от возраста. В таком случае при сопоставлении данных о функции органов и систем (таких как частота дыхания, частота сердечных сокращений, величина артериального давления, количество клеток крови, биохимические показатели крови и др.) у детей выделенных групп неправильным является использование средних величин, так как возрастной состав пациентов сравниваемых групп может существенно различаться.
Число свойств. Важной особенностью алгоритма AprioriScale является то, что набор свойств объекта имеет тип перечисления, представленного шкалой. Но это означает, что каждому свойству ставится в соответствие число 2 в степени k. При проецировании перечисления на целочисленный тип ulong это означает, что максимальное число свойств не должно быть больше 64.
Можно заметить, что для исследователя, занимающегося анализом ассоциативных правил, 60 – это большое число. Так что вряд ли при построении правил следует вводить более 60 свойств. Тем не менее, если такая задача возникает, то можно модифицировать алгоритм так, чтобы он учитывал такую ситуацию. Для этого достаточно исходное число свойств разбить на группы, в каждой из которых число свойств будет менее 60.
Правила можно строить как внутри каждой группы, так и связывая параметры разных групп, например, посылка правила принадлежит одной группе свойств, а заключение принадлежит другой группе.
Недавно одному из авторов данной статьи пришлось анализировать результаты обработки большой БД покупок в супермаркете, содержащей около сотни тысяч записей. Данные обрабатывались с использованием инструментов Data Mining for Excel и Microsoft SQL Server. Данные не подвергались предварительной обработке, поэтому в записях присутствовали десятки названий сортов водки, пива, вина. Это касалось не только алкоголя, но и других видов продукции. В результате правила и рекомендации не представляли особого интереса, были в основном одиночными – типа «водка беленькая – селедка тихоокеанская». Конечно, такая БД без предварительной обработки не может использоваться в алгоритме AprioriScale. Но подобную базу непосредственно и не следует использовать для построения ассоциативных правил. Вероятно, следовало разбить алкогольную продукцию на три группы в соответствии с ценами – средние цены, высокие и низкие. В этом случае правила могли нести более содержательную информацию. Вообще предварительный этап подготовки данных в соответствии с задачами исследователя играет важную роль в получении не только достоверных, но и несущих содержательный смысл для исследователя правил.
Параллельные версии. В основе построения ассоциативных правил лежит работа с БД, возможно, большого размера. В этой ситуации существует естественное распараллеливание по данным, что позволяет реализовать параллельные версии алгоритма. Конечно, если время построения правил находится в пределах нескольких секунд, распараллеливание вычислений не имеет особого смысла, а лишь усложняет алгоритм и его отладку. Тем не менее, параллельные версии могут быть весьма полезны как для очень больших БД, так и при большом числе свойств. Особенности построения параллельных алгоритмов и обсуждение возникающих в этом случае проблем приведено в [7, 8].
О времени работы алгоритма
Из описания алгоритма следует, что он должен работать эффективно. Приведем результаты экс- перимента, где оценивалось время построения правил в зависимости от размера БД. Исходная БД, используемая для решения задач медицинской диагностики, была относительно небольшой и содержала 150 записей. Чтобы оценить время решения на больших базах, данные исходной базы копировались и были построены БД на 2 000 записей и 20 000 записей. При размере БД 150, 2 000 и 20 000 записей время вычисления ассоциативных правил составляет 28, 57, 342 миллисекунды соответственно.
Эти данные подтверждают линейный характер зависимости времени вычислений от размера БД. Они также свидетельствуют о малом значении коэффициента в этой зависимости. БД из 20 000 записей обрабатывается менее одной секунды.
Задача медицинской диагностики и построение ассоциативных правил. Рассмотрим задачу диагностики в медицине и посмотрим, как построение ассоциативных правил может помочь в решении задач, стоящих перед медиками. Общая постановка задачи такова. Объектами в задаче являются пациенты. БД db содержит сведения о пациентах и их заболеваниях. Среди свойств, характеризующих пациента, выделены бинарные свойства, влияющие, по мнению медиков, на возникновение за- болеваний, имеющихся у пациентов. Медиков интересуют ассоциативные правила вида XÞP, где X – совокупность измеряемых факторов, с высокой достоверностью приводящая к появлению заболевания P. Для них также крайне важно определить, является ли совокупность факторов X классифицирующей, то есть таковой, что появление X с высокой вероятностью свидетельствует о возможном появлении заболевания P, тогда как достоверность правил XÞQ низкая, когда Q – другое заболевание, отличное от P.
Дальнейшее рассмотрение будем вести на примере конкретной задачи из области педиатрии, когда рассматривается БД, содержащая данные о детях, страдающих различными заболеваниями – ожирением и метаболическим синдромом [9, 10]. Указанные патологические состояния объединены наличием общего признака – ожирения. Однако, согласно современным представлениям [11–14], метаболический синдром диагностируется у детей, имеющих, помимо ожирения, еще целый ряд дополнительных признаков.
Подготовленная медиками БД построена на основании результатов многолетних наблюдений. Ее особенность в том, что для детей в возрасте 13–14 лет, которым поставлен диагноз «ожирение» или «метаболический синдром», имеются данные, полученные на самых ранних этапах его развития. Свойства, сохраняемые в БД, относятся к трем периодам: беременность матери, непосредственно роды и первые недели жизни ребенка. Эти свойства традиционно рассматриваются в медицине в качестве факторов риска. Традиционным подходом при анализе данных медицинских исследований является выделение наиболее значимых факторов риска.
Согласно современным представлениям, большинство патологических состояний развивается в результате воздействия не одного, а совокупности факторов риска, то есть является многофакторной проблемой. В связи с этим актуальной задачей медицинских исследований является выделение комплекса факторов, способствующих развитию той или иной патологии, получение количественного и/или качественного представления о суммарном интегральном риске [15].
Перед медиками стоят две задачи.
1. Выявить, какие совокупности параметров, то есть факторы риска, определяемые на ранних этапах развития ребенка, могут свидетельствовать о возникновении заболеваний в подростковом возрасте. В случае выявления таких совокупностей может быть разработан комплекс мероприятий по снижению риска или, если факторы риска являются управляемыми и могут быть устранены, по предотвращению развития данного патологического состояния. Тем самым может быть решена задача по первичной профилактике данной патологии.
2. Определить возможность различения (дифференцирования) ожирения и метаболического синдрома. По данному вопросу в настоящее время не существует единого мнения, ибо в литературе метаболический синдром рассматривается и как осложнение ожирения, и как самостоятельная нозологическая форма.
Одна из практических целей данной работы состоит в анализе того, можно ли из накопленной БД извлечь ассоциативные правила, помогающие медикам в решении их задач (табл. 1–3).
Приведем несколько исходных записей БД.
Таблица 1
Общие характеристики пациентов
Table 1
Patients’ general characteristics
|
Вес при рождении
|
Рост при рождении
|
Возраст
|
Вес
|
Рост
|
Диагноз
|
|
3,5
|
55
|
13
|
100
|
151
|
МС
|
|
3,7
|
52
|
14
|
117
|
174
|
МС
|
|
3,5
|
54
|
14
|
84
|
166
|
ОЖ
|
Таблица 2
Первая группа анализируемых факторов
Table 2
The first group of analysed factors
|
Токсикоз
|
УПБ
|
ЭЗМ
|
ОВБЗ
|
Проф_В
|
НЕД
|
ХВ
|
RH
|
|
Да
|
Да
|
Да
|
Да
|
Да
|
|
|
|
|
Да
|
Да
|
Да
|
|
|
|
|
|
|
Да
|
Да
|
|
|
Да
|
|
|
|
Таблица 3
Вторая и третья группы анализируемых факторов
Table 3
The second and the third group of analysed factors
|
Кесс
|
Слаб_РД
|
Стрем_Р
|
Остр_Асф
|
Пособия
|
АПГАР
|
ППГ
|
ПОП
|
| |
|
|
|
Да
|
Да
|
Да
|
|
|
Да
|
Да
|
|
|
|
|
|
|
|
Да
|
Да
|
|
|
|
|
Да
|
Да
|
Реализация алгоритма AprioriScale на языке C#
Рассмотрим ключевые моменты реализации алгоритма на языке программирования C#.
Задание перечисления. Класс Properties представляет перечисление анализируемых факторов, включая диагнозы. Вот его описание:
[Flags]
public enum Properties
{
Токсикоз =1<<0, УПБ=1<<1, ЭЗМ=1<<2, ОВБЗ=1<<3,
Проф_В = 1<<4, НЕД = 1<<5, ХВ = 1<<6, RH = 1<<7,
Кесс = 1 << 8, СлабРД = 1 << 9, СтремР = 1 << 10,
Остр_Асф = 1 << 11, Пособия = 1 << 12,
АПГАР = 1 << 13, ППГ = 1 << 14, ПОП = 1 << 15,
МС = 1 << 16, ОЖ = 1 << 17
}
В перечислении указаны все 18 анализируемых факторов. Атрибут класса [Flags] и указание для каждого элемента числа, задающего внутреннее представление элемента, показывает, что перечисление является шкалой. Запись 1≪k является C# аналогом математической записи 2k.
Построение правил. Основной метод построения правил достаточно прост, так что можно привести его полную реализацию:
///
/// Создание списка правил
/// Основной метод
///
public void Create_Rules()
{
Create_Rules_1();
bool exist_new_rules = true;
while(exist_new_rules)
{
exist_new_rules = Create_Rules_K();
}
}
Вначале создается список правил, где посылка и заключение имеют длину 1, то есть содержат по одному элементу. Затем в цикле по уже построенным правилам и множеству частых примеров длины k–1 строятся правила длины k, когда на 1 расширяется длина посылки и/или заключения. Процесс построения заканчивается, когда новые правила построить не удается.
Функция Support. Как уже отмечалось, функция Support при данном выборе представления данных имеет линейную сложность и вычисляется просто:
///
/// Поддержка объекта в БД
///
///объект, для набора свойств которого
/// вычисляется поддержка(частота появления в БД)
/// частота появления набора
public double Support(Bask bask)
{
double count = 0;
foreach (Bask item in db)
{
if ((bask.Bask_prop & item.Bask_prop) == bask.Bask_prop)
count++;
}
return count / n;
}
В цикле по записям БД счетчик count увеличивается на единицу, если все свойства объекта bask содержатся в записи БД. Выражение if построено в полном соответствии с ранее приведенным выражением (13).
Построение частых наборов и правил длины 1. Метод Create_Rules_1, строящий список частых примеров и правил длины 1, достаточно прост и понятен. Его реализация очевидна, так что нет необходимости приводить его полный текст. Достаточно лишь упомянуть, что редкие одиночные свойства и недостоверные правила в соответствии с принципом антимонотонности удаляются из дальнейшего рассмотрения.
Построение частых наборов и правил дли- ны k. Метод Create_Rules_k, строящий достоверные правила длины k, является центральным методом в реализации алгоритма. Его основные идеи достаточно подробно описаны. Приводить здесь его полную реализацию на языке программирования не имеет смысла.
Инструментарий для решения задач медицинской диагностики
Для проведения исследований и решения задач, стоящих перед медиками, авторами был разработан программный инструментарий. Его главной задачей является построение на основе алгоритма AprioriScale достоверных ассоциативных правил, извлекаемых из БД. Не менее важным являлось со- здание средств, удобных для проведения анализа правил, выбор из множества правил тех, которые имеют содержательный смысл и позволяют отвечать на поставленные медиками вопросы.
Основная форма построения правил. На рисунке 1 показана основная форма, позволяющая создавать правила на основе заданной БД и граничных характеристик частоты и достоверности правил.
Элемент управления ListBox «Факторы» содержит cписок анализируемых свойств в краткой форме, в которой они используются в правилах, и их более полное содержательное описание.
Элемент управления ListBox «Базы данных» содержит список БД, которые могут использоваться для построения правил.
Два текстовых поля «Частота правил» и «Качество (достоверность) правил» содержат минимальные значения частоты и качества правила, ниже которых правила не строятся.
Ряд командных кнопок позволяют пользователю выполнять различные действия, необходимые для построения правил.
Выбрав из списка БД и нажав кнопку «Выбрать базу», получаем имя БД, с которой будем работать, и путь к соответствующему файлу, хранящему БД.
Задав в текстовых полях значения минимальной частоты и минимального качества и нажав кнопку «Задать характеристики», получаем характеристики правил, которые будут использоваться при построении правил.
Нажатие кнопки «Связаться с БД» приводит к открытию соответствующей БД.
Нажатие кнопки «Показать БД» приводит к отображению соответствующей БД в элементе управления ListBox «База данных».
Предполагается, что командные кнопки нажимаются в указанном порядке. Если БД открыта и характеристики правил заданы, при нажатии кнопки «Построить правила» строятся ассоциативные правила, частота и достоверность которых выше заданных минимальных характеристик.
Последняя в ряду командная кнопка «Перейти к работе с правилами» открывает новую форму.
 Важную роль играет текстовое окно «Сообщение». При нажатии каждой командной кнопки в этом окне появляется информация о результатах выполнения действия, заданного командной кнопкой. Если действие выполнено в соответствии со спецификациями, сообщение подтверждает успешность его выполнения. Так, на рисунке 1 показано, что после нажатия командной кнопки «Построить правила» в окне «Сообщение» отображается текст, уведомляющий, что правила успешно построены и на их построение потребовалось 28 микросекунд. Если же по каким-либо причинам действие выполнить не удалось, в окне появляется сообщение, указывающее причину невыполнения. Например, если пользователь нажал кнопку «Выбрать базу», не выбрав предварительно базу в списке БД, появится сообщение: «Выберите из списка имя БД, после чего нажмите кнопку <Выбрать базу>».
Важную роль играет текстовое окно «Сообщение». При нажатии каждой командной кнопки в этом окне появляется информация о результатах выполнения действия, заданного командной кнопкой. Если действие выполнено в соответствии со спецификациями, сообщение подтверждает успешность его выполнения. Так, на рисунке 1 показано, что после нажатия командной кнопки «Построить правила» в окне «Сообщение» отображается текст, уведомляющий, что правила успешно построены и на их построение потребовалось 28 микросекунд. Если же по каким-либо причинам действие выполнить не удалось, в окне появляется сообщение, указывающее причину невыполнения. Например, если пользователь нажал кнопку «Выбрать базу», не выбрав предварительно базу в списке БД, появится сообщение: «Выберите из списка имя БД, после чего нажмите кнопку <Выбрать базу>».
Форма для работы с построенными правилами. После того как в основной форме построены правила и нажата командная кнопка «Перейти к работе с правилами», открывается новая форма, позволяющая выполнять некоторые действия над правилами.
Основная операция, выполняемая на этом этапе, – фильтрация правил. Алгоритм чаще всего строит правила, лишь часть из которых интересуют исследователя при решении его специфических задач. Поэтому возникает необходимость фильтрации правил. Конечно, фильтр можно было бы за- давать еще на этапе построения правил, но это осложнило бы алгоритм построения. Учитывая, что правила строятся быстро, удобнее иметь возможность задавать фильтр для уже построенного полного множества правил.
 На рисунке 2 показана форма для работы с построенными правилами.
На рисунке 2 показана форма для работы с построенными правилами.
Два элемента управления ListView отображают в нескольких столбцах все исследуемые свойства. В каждом из них можно выбрать ряд свойств. В элементе управления «Посылка правила» задаются свойства, накладываемые фильтром на посылку правила. Фильтр из всех правил будет отби- рать лишь те, свойства которых содержатся в свойствах, заданных фильтром. На рисунке 2 показано задание фильтра посылки правила. В этом случае из рассмотрения исключаются правила, посылка которых содержит свойства, указывающие на диагноз МС и ОЖ. Аналогично в элементе управления «Заключение правила» можно выбрать свойства, которые будут включаться в заключение правила.
Выбрав свойства в «Посылке правила» и нажав командную кнопку «Задать посылку фильтра показа», задаем первую часть фильтра – фильтр посылки правил. Аналогично, выбрав свойства в «Заключении правила» и нажав командную кнопку «Задать заключение фильтра показа», задаем вторую часть фильтра – фильтр заключения правила. После этого можно перейти к показу отфильтрованных правил, нажав командную кнопку «Перейти к показу правил».
Еще одна полезная возможность, предоставляемая этим инструментом, состоит в том, что исследователя может интересовать некоторое конкретное правило. Используя те же элементы управления «Посылка правила» и «Заключение правила», можно выбрать свойства, которые будут включены в посылку и заключение конкретного правила. Командные кнопки «Задать посылку индивидуального правила» и «Задать заключение индивидуального правила» выполняют указанные действия. Командная кнопка «Построить индивидуальное правило» строит правило с заданной посылкой и заключением, рассчитывает его характеристики – частоту и достоверность – и выводит результаты в текстовое окно «индивидуальное правило». На рисунке 2 показан результат построения одного из таких правил.
 Форма показа правил. На рисунке 3 показана форма завершающего этапа работы с правилами.
Форма показа правил. На рисунке 3 показана форма завершающего этапа работы с правилами.
Нажав командную кнопку «Показать правила», в списке «Правила» можно видеть все правила, соответствующие фильтру, построенному на предыдущем этапе. Командная кнопка «Показать все правила» позволяет просмотреть полный список построенных ассоциативных правил без учета фильтрации. Правила, отображаемые в окне списка, можно сохранить в файле, имя которого указывается в соответствующем текстовом окне. Результат выполнения этой операции и полный путь к файлу отображаются в окне «Сообщение».
 На рисунке 4 показан сохраненный файл правил, открытый в блокноте.
На рисунке 4 показан сохраненный файл правил, открытый в блокноте.
Анализ результатов
Алгоритм построения ассоциативных правил может применяться в разных ситуациях. При анализе БД, где записями являются корзины покупателей, содержащие различные товары, все товары имеют один и тот же статус. В торгующем книгами интернет-магазине покупателю, положившему в корзину некоторую книгу, рекомендуют и другие книги. Рекомендации построены на основе правил, определяющих, какие книги обычно заказывают в сочетании с выбранной книгой.
В задачах медицинской диагностики свойства имеют различный статус: одни представляют диагнозы, другие – факторы, влияние которых на возникновение того или иного заболевания и является целью исследования. Как и в рассматриваемой ав- торами конкретной медицинской задаче, факторы могут относиться к различным временным периодам.
Прежде всего медиков интересуют ассоциативные правила, связывающие измеряемые факторы и заболевания. Если эти правила обладают высокой степенью достоверности, они могут свидетельствовать о рисках появления заболевания, когда у пациента обнаруживаются факторы, стоящие в посылке правила.
Если факторы риска выявляются на ранних стадиях, заболевание можно предотвратить или, по крайней мере, ослабить его тяжесть.
Рассмотрим вопрос о репрезентативности данных. Как уже отмечалось, БД состоит из 150 записей. БД такого размера относятся к малым БД. Можно ли доверять результатам, построенным на базах такого размера? Можно, если выборка, представленная БД, сохраняет свойства генеральной совокупности. Фактически важен не столько сам размер БД, сколько ее репрезентативность, то, насколько эта база отражает генеральную совокупность. Уже отмечалось, что, увеличив размер БД до 20 000 записей путем их репликации, никакой дополнительной информации не получено. Базы и на 150 записей, и на 20 000 записей в одинаковой степени отражают свойства генеральной совокупности. В данном случае генеральную совокупность составляет множество детей, страдающих указанными недугами. Число их не столь велико. Можно считать, что в приведенной в статье выборке представлена существенная часть детей Тверской области.
Рассмотрим построенные правила и проанализируем их. На рисунке 4 показаны двадцать девять правил, прошедших фильтрацию. Их достоверность превосходит значение 0,5, которое выбрано в качестве порогового значения. Рассмотрим первое из этих правил: Токсикоз Þ МС, частота = 0,49, достоверность = 0,53. Заметим, что среди построенных правил нет правила Токсикоз Þ ОЖ. Наш инструмент позволяет построить такое правило и оценить его характеристики. Выполним этот эксперимент. Вот соответствующее правило: Токси- коз Þ ОЖ, частота = 0,44, качество = 0,47. Правило не попало в список из-за ограничений на качество правила. Высокая частота обоих правил, близкая к максимальной, в данном случае равной 0,5, говорит о том, что токсикоз сопровождает оба заболевания. Что касается достоверности правил, то оба они имеют близкие значения, не позволяющие фактически различать заболевания на основании одного этого признака. Заметим, что в нашей выборке каждая запись содержит один из двух диагнозов – МС или ОЖ. Потому правила с одной и той же посылкой, но с разными диагнозами связаны по достоверности. Если достоверность правила X Þ MC равна P, то достоверность правила X Þ ОЖ равна 1–P. По этой причине правила, имеющие достоверность в пределах 0,5–0,7, по сути не могут использоваться для различения диагнозов.
Правила, позволяющие отличать один диагноз от другого, должны иметь высокую степень достоверности. И такие правила в нашем случае есть. Можно видеть, что существуют 12 правил, досто- верность которых выше 0,75. Все они указывают на метаболический синдром. В целом это позволяет сделать важный с точки зрения медиков вывод о том, что по результатам наблюдений, выполненных на ранних стадиях, можно выявить риск возникновения метаболического синдрома у детей, склонных к ожирению.
Проанализируем более подробно два из таких правил:
Токсикоз, УПБ, СлабРД Þ МС частота = 0,16 качество = 0,83;
Токсикоз, УПБ, ЭЗМ, ППГ Þ МС частота = 0,09 качество = 0,93.
Заметим, что альтернативные правила с той же посылкой, свидетельствующие об ожирении, не сопровождаемом метаболическим синдромом, имеют вид
Токсикоз, УПБ, СлабРД Þ ОЖ частота = 0,03 качество = 0,17;
Токсикоз, УПБ, ЭЗМ, ППГ Þ ОЖ частота = 0,01 качество = 0,07.
Переходя от частоты и достоверности к соотношениям в БД, можно видеть, что первое из этих правил основано на том, что из 30 пациентов, имеющих подобное сочетание тройки факторов, у 25 впоследствии имел место метаболический синдром. Отсюда следует, что вероятность проявления этого синдрома при таком сочетании факторов равна 0,83.
Еще более впечатляют результаты второго правила. Если у пациента встретилась четверка факторов, то вероятность метаболического синдрома равна 0,93, в то время как вероятность проявления только ожирения равна 0,07.
В целом правила, извлекаемые из БД, позволяют сделать следующий вывод: если на ранних стадиях развития ребенка наблюдаются такие факторы, как Токсикоз, УПБ, ЗЗМ, сопровождаемые позже такими факторами, как СлабРД, ППГ, то риск проявления метаболического синдрома велик, вероятность его проявления находится в пределах 0,8–0,9.
Таким образом, в работе предложен эффективный алгоритм построения ассоциативных правил, имеющий линейную сложность относительно размера БД, построен программный инструментарий на языке C#, достаточно удобный при проведении исследований в процессе построения ассоциативных правил, извлекаемых из БД.
Алгоритм с успехом был применен для решения конкретной задачи медицинской диагностики.
Построенные ассоциативные правила позволили сделать важный вывод о возможности выявления на ранних стадиях параметров, свидетельствующих о риске возникновения метаболического синдрома.
Предложенный алгоритм и программный инструментарий могут с успехом применяться при решении различных задач диагностики в медицине, а также в других прикладных областях.
Литература
1. Agrawal R. and Srikant R. Fast algorithms for mining association rules in large databases. Proc. 20th Intern. Conf. on Very Large Data Bases, VLDB, 1994, pp. 487–499.
2. Olson D.L., Delen D. Advanced Data MiningTechniques. Springer, 2008, p. 181.
3. Vercellis C. Business Intelligence: Data Mining and Optimization for Decision Making. Willey, 2009, p. 436.
4. Zhao Y., Zhang C., Cao L. Post-Mining of Association Rules: Techniques for Effective Knowledge Extraction. Information sc. reference, Hershey, NY, 2009, p. 394.
5. Hahsler M. A probabilistic comparison of commonly used interest measures for association rules, 2015. URL: http://michael.hahsler.net/research/association_rules/measures.html (дата обращения: 12.12.2015).
6. Биллиг В.А. Основы программирования на С#. М.: ИНТУИТ, Бином, Лаборатория знаний, 2009. 582 с.
7. Биллиг В.А. Оценки времени в модели параллельного выполнения программ // Программные продукты и системы. 2012. № 4 (100). С. 183–188.
8. Биллиг В.А. Параллельные вычисления и многопоточное программирование. М.–Тверь: ИНТУИТ–ЗАО НИИ ЦПС, 2013. 232 с.
9. Царегородцев Н.А. Оценка факторов, определяющих здоровье, у детей с метаболическим синдромом // Порядок и стандарты оказания помощи детям с эндокринными заболеваниями: матер. IX Всерос. науч.-практич. конф. детских эндокринологов. Архангельск, 2013. С. 39–40.
10. Иванова О.В., Царегородцев Н.А. Методические аспекты педиатрического преподавания в медицинском вузе // Сб. трудов ТГМА, Тверь, 2011. С. 130–138.
11. Балыкова Л.А. и др. Метаболический синдром у детей и подростков // Педиатрия. 2010. Т. 89. № 3. С. 127–134.
12. Синицын П.А. и др. Метаболический синдром у детей // Педиатрия. 2008. Т. 87. № 5. С. 124–137.
13. Козлова Л.В. и др. Метаболический синдром у детей и подростков с ожирением: диагностика, критерии рабочей классификации, особенности лечения // Педиатрия. 2009. Т. 88. № 6. С. 142–150.
14. Zimmet P., Alberti G., Kaufman F., Tajima N. The metabolic syndrome in children and adolescents – an JDF consensus report. Pediatric Diabetes, 2009, vol. 8, pp. 299–306.
15. Рахимова Г.Н., Азимова Ш.Ш. Интегральная оценка факторов риска развития метаболического синдрома у детей и подростков с ожирением // Детская эндокринология. 2012. № 3 (43). С. 77–81.



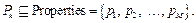 (3)
(3) . (6)
. (6) . (8)
. (8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (14)
(14) (15)
(15)



