Авторитетность издания
ВАК - К1
RSCI, ядро РИНЦ
Добавить в закладки
Следующий номер на сайте
№3
Ожидается:
13 Сентября 2024
Исследование комбинированного алгоритма при обучении трехслойных нейронных сетей различной топологии
Investigation of a combined algorithm for learning three-layer neural networks of different topologies
Дата подачи статьи: 24.07.2018
УДК: 004.852
Статья опубликована в выпуске журнала № 4 за 2018 год. [ на стр. 673-676 ]Аннотация:При обучении нейронной сети настройка весовых коэффициентов осуществляется на основе минимизации ошибки вычислений. В случаях, когда целевая функция имеет сложный характер и обладает большим количеством локальных экстремумов, обучение сети с применением градиентных методов оптимизации зачастую не гарантирует нахождение глобального экстремума. Решение этой проблемы на сегодняшний день для большого класса задач осуществляется с помощью генетических алгоритмов как основного метода для обучения сетей обратного распространения ошибки. Развитие этих алгоритмов получило свое продолжение в изучении биоинспирированных алгоритмов и их гибридных модификаций. Использование биоинспирированных алгоритмов, основанных на методах случайного поиска, позволяет решить проблему обхода локальных экстремумов и обладает высокой скоростью сходимости. В работе рассматривается комбинированный биоинспирированный алгоритм, реализующий решение задачи глобальной оптимизации в случае проблем, связанных с обучением искусственных нейронных сетей. Структура сети и число нейронов в каждом скрытом слое являются важными параметрами, влияющими на эффективность обучения искусственных нейронных сетей. Трехслойные нейронные сети позволяют решать большинство сложных задач. Однако влияние количества нейронов в каждом из скрытых слоев на скорость сходимости в общем случае мало изучено. В работе исследуется ранее разработанная авторами комбинация алгоритма светлячков и градиентного спуска для обучения трехслойных нейронных сетей различной топологии. Проведенное исследование дало возможность выявить из рассмотренных искусственных нейронных сетей топологию, позволяющую получить наиболее оптимальное решение за меньшее количество шагов. Анализ производительности алгоритма обучения осуществлен на основе функции «исключающее ИЛИ» (Xor).
Abstract:When learning a neural network, the weighting factors are adjusted based on minimizing a calculation error. When the objective function has a complex character and a big number of local extremums, network learning using gradient optimization methods does not often guarantee the finding of a global extremum. Nowadays, the solution of this problem for a large class of problems includes using genetic algorithms as the main method for learning backpropagation networks. The development of these algorithms has continued in the study of bioinspired algorithms and their hybrid modifications. The use of bioinspired algorithms, which are based on random search methods, allows solving the problem of bypassing local extremums and has high convergence rate. The paper considers a combined bioinspired algorithm that solves the global optimization problem when there are problems associated with learning artificial neural networks. The network structure and the number of neurons in each hidden layer are important parameters affecting the effectiveness of artificial neural networks learning. Three-layer neural networks can solve many complex problems. However, the effect of the number of neurons in each hidden layer on the convergence rate is under-explored in the general case. The paper studies a combination of the firefly algorithm and gradient descent developed by the authors for the study of three-layer neural networks of various topologies. The conducted research made it possible to identify topology from artificial neural networks. This topology makes it possible to obtain the most optimal solution for fewer steps. The analysis of the learning algorithm performance is based on the exceptional-OR (Xor) function.
| Авторы: Остроух Е.Н. (eostr@donpac.ru) - Донской государственный технический университет (доцент), Ростов-на-Дону, Россия, кандидат технических наук, Евич Л.Н. (bkln@mail.ru) - Донской государственный технический университет (доцент), Ростов-на-Дону, Россия, кандидат физико-математических наук, Чернышев Ю.О. (sergeev00765@mail.ru) - Донской государственный технический университет (профессор), Ростов-на-Дону, Россия, доктор технических наук, Маркин С.Д. (potate82@ya.ru) - Донской государственный технический университет (магистрант), Ростов-на-Дону, Россия, Панасенко П.А. (we_panasenko_777@mail.ru) - Краснодарское высшее военное училище им. генерала армии С.М. Штеменко (преподаватель), Краснодар, Россия, кандидат технических наук | |
| Ключевые слова: алгоритмы оптимизации, нейронная сеть, алгоритм светлячков, градиентный спуск |
|
| Keywords: optimization algorithms, neural network, Firefly Algorithm, gradient descent |
|
| Количество просмотров: 7567 |
Статья в формате PDF Выпуск в формате PDF (22.98Мб) |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4523 |
Версия для печати Выпуск в формате PDF (22.98Мб) |
| Статья опубликована в выпуске журнала № 4 за 2018 год. [ на стр. 673-676 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Разработка нейронной сети для оценки исправности гидроагрегата по результатам вибромониторинга
- Кластеризация документов проектного репозитария на основе нейронной сети Кохонена
- Интеллектуальные системы и алгоритмы управления объектами обстановки в тренажерах
- Информационная и алгоритмическая поддержка интеллектуальной системы экологического мониторинга воздуха на основе нейронных сетей
- Система поддержки принятия решений при определении нозологической формы гепатита
Назад, к списку статей



 ,
,
 .
.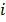 . Новое расположение светлячка с номером
. Новое расположение светлячка с номером  вычисляем по формуле
вычисляем по формуле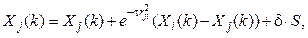
 и переходим к шагу С4. Если i = j = N, завершаем алгоритм.
и переходим к шагу С4. Если i = j = N, завершаем алгоритм.

