Программные продукты и системы

В настоящее время в области машинного обучения имеется тенденция к повышению сложности используемых нейронных сетей и наборов данных. Это в значительной степени обусловлено переходом на GPU-вычисления и увеличением доступных для данных задач вычислительных ресурсов. Кроме того, появление новых программных библиотек для глубокого обучения расширило возможности для проведения экспериментов [1]. Термин «глубокое обучение» относится к обучению нейронных сетей, имеющих более одного скрытого слоя [2]. Распространенными примерами глубоких нейронных сетей в настоящее время являются сверточные нейронные сети [3] и некоторые виды рекуррентных нейронных сетей [4]. Помимо непосредственного использования глубоких нейронных сетей для задач компьютерного зрения, статистического анализа, обработки естественного языка и других, продолжаются исследования в направлении архитектур, объединяющих для решения своей задачи входные данные различных типов (например, текст и визуальный сигнал), применяя при этом несколько различных архитектур глубоких нейронных сетей в одной системе. В частности, при разработке визуальных вопросно-ответных систем используются достижения из областей компьютерного зрения и обработки естественного языка. Задача системы заключается в том, чтобы дать ответ на заданный в произвольном виде вопрос о предоставленном изображении или видеопоследовательности [5]. Ответы могут быть односложными («да» или «нет»), числовыми (в случае с вопросами о количестве) или представлять собой список возможных вариантов [6]. Основное отличие визуальных вопросно-ответных систем от других подобных систем в том, что тип вопроса и его структура неизвестны до момента выполнения запроса.

Поскольку вопрос заранее неизвестен, система должна обладать высокой степенью обобщения. Использование нескольких типов входных данных и архитектур глубоких нейронных сетей требует решения дополнительных задач, связанных с методами объединения входных данных различной природы, а также проблемы роста количества параметров, особенно существенной в случае применения билинейного объединения данных. Одним из способов оптимизации размерности в данных системах является применение методов тензорного разложения.

В данной работе предложена модификация алгоритма обучения визуальной вопросно-ответной системы, позволяющая оптимизировать параметры блочного тензорного разложения непосредственно в процессе обучения системы, снимая необходимость гиперпараметрической оптимизации, связанной с компонентом тензорного разложения в системе.

Системы могут применяться, в частности, при разработке приложений для людей с плохим зрением и в других задачах, где требуются универсальное распознавание и извлечение данных из визуального сигнала. Интерес исследователей вызван также и тем, что задача связана с разработкой универсальных систем машинного обучения, то есть систем, рассчитанных на широкий круг задач.

Решение данной задачи объединяет в себе использование научных разработок в области компьютерного зрения и обработки естественного языка. Методы компьютерного зрения используются для анализа визуального компонента входных данных и позволяют системе с помощью алгоритма машинного обучения находить модели распознавания визуальных паттернов и структуры сцены. Методы обработки естественного языка в данной задаче используются для анализа текста вопроса и формирования ответа в текстовом виде на основе как самого вопроса, так и визуальных данных. В данном случае изображение или видеопоследовательность могут рассматриваться (в контексте архитектуры нейронных сетей) как дополнительная информация для ответа на вопрос. Объединение текстовых и визуальных данных в системе машинного обучения имеет свои сложности (которые будут более подробно рассмотрены далее), связанные с различиями в размерности, в степени зашумленности, а также закономерности в данных.

По способу объединения входных данных различных модальностей визуальные вопрос-но-ответные системы можно разделить на два класса: модели на основе объединенного представления и билинейного объединения. В первом случае текст и изображение отображаются на общее пространство признаков путем конкатенации либо поэлементных операций умножения или сложения. В билинейных моделях для объединения входных данных используется тензорное произведение следующего вида: m = W[x ⊗ q], где x ∈ ℝI и q ∈ ℝJ – тензоры входных данных; W ∈ ℝK – тензор весовых коэффициентов; ⊗ – внешнее произведение; [] – операция линеаризации.

Билинейные модели позволяют находить (с помощью алгоритма обучения) как более сложные зависимости между входными и выходными данными, так и взаимосвязи между входными данными разной модальности, то есть в данном случае между текстом и изображением.

Одной из сложностей при разработке билинейных моделей является высокая размерность тензора, получаемого при тензорном умножении входных данных, что ведет к большому числу параметров модели и, соответственно, к таким проблемам, как высокие требования к видеопамяти (поскольку обучение данных систем чаще всего осуществляется с помощью GPU), времени вычислений, а также подверженности эффекту переобучения. Для уменьшения количества параметров в билинейных моделях применяются методы снижения размерности и тензорного разложения. Среди данных методов можно выделить аппроксимацию с помощью алгоритма Count-Sketch [7] и систему мультимодального билинейного объединения (Multimodal Bilinear Pooling), предложенную в [8]. К применимым в данной задаче алгоритмам тензорного разложения относятся каноническое разложение (Canonical Polyadic Decomposition, CANDECOMP, другое название – PARAFAC), разложение Такера и блочное тензорное разложение [9].

Разработка более эффективных методов снижения размерности в данных системах означает уменьшение вероятности переобучения, а также возможность использования освободившихся ресурсов для дальнейших улучшений архитектуры применяемых нейронных сетей, возможность применения большего размера мини-пакета при обучении и увеличение максимально допустимого разрешения изображений для более гранулированного извлечения признаков.

В статье рассматривается модифицирован-ный интеллектуальный алгоритм обучения ви-зуальной вопросно-ответной системы, отличающийся от аналогов использованием компонента регуляризации для блочного тензорного разложения. Компонент дает возможность аппроксимировать оптимальный размер и количество блоков для текущей модели и набора данных, позволяя увеличить точность и скорость нахождения данных параметров.

Блочное тензорное разложение

Метод блочного тензорного разложения (Block-term tensor decomposition, BTD) был предложен в работе [10]. Данный тип объединяет в себе сильные стороны канонического разложения и разложения Такера.

Разложение Такера для случая тензора размерности T ∈ RI×J×K имеет следующий вид:

,

где A ∈ ℝI×P, B ∈ ℝI×Q, C ∈ ℝI×R – факторные матрицы; D ∈ ℝP×Q×R – центральный тензор, отражающий зависимости между факторными матрицами; ×n – тензорное умножение в размерности n.

Блочное тензорное разложение представляет собой сумму нескольких разложений Такера: , где R – количество блоков.

В работе [11] была представлена реализация визуальной вопросно-ответной системы с использованием блочного тензорного разложения. Это позволило уменьшить количество параметров модели, что привело к более эффективному использованию памяти и снизило вероятность переобучения. Однако такие параметры, как количество блоков и их размер, в данной модели были подобраны вручную. При использовании другого набора данных или изменении архитектуры используемых нейронных сетей потребуется провести несколько новых экспериментов, в ходе которых могут быть определены другие оптимальные значения этих гиперпараметров. Ручная настройка данных гиперпараметров требует дополнительного времени и может быть не настолько точной, как в случае с подбором этих параметров в результате работы алгоритма обучения. Поэтому в данной статье рассматривается метод аппроксимации этих параметров, применяемый во время обучения системы.

Аппроксимация размера и количества элементов в блочном тензорном разложении

Задача аппроксимации тензора T ∈ ℝI×J×K с помощью метода наименьших квадратов имеет следующий вид:

,

где R – количество блоков; Lr, r = [1, 2, …, R] – размер каждого блока. При этом Ar = [ar1, ar2, …, arLr] ∈ , Br = [br1, br2, …, brLr] ∈ 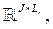 C ∈ ℝK×R.

Значения R и Lr зачастую неизвестны заранее. Параметры неизвестны при разработке новой визуальной вопросно-ответной системы, они могут изменяться при использовании другого набора данных или значительного изменения архитектуры существующей системы. Одним из решений данной проблемы может быть добавление дополнительных штрафов в функцию потерь, целью которых будет минимизация размера блоков и их количества, что позволит находить оптимальные значения для данных параметров непосредственно в процессе обучения системы. При этом значения параметров инициируются завышенными значениями в предположении, что они будут постепенно уменьшаться до оптимальных за счет регуляризации в процессе работы алгоритма обучения.

В работе [12] задачи аппроксимации размерности модели и факторных матриц решаются параллельно. Целевая функция для алгоритма блочного тензорного разложения модифицирована новым компонентом: изначальный критерий (среднеквадратическая ошибка аппроксимации тензора) дополняется смешанной ℓ1,2 нормой факторных матриц:

,

где g – параметр регуляризации; ||⋅||F – норма Фробениуса; ||⋅||F – смешанная ℓ1,2 норма (ℓ1 норма ℓ2 норм столбцов матрицы, способствующая увеличению разреженности столбцов и снижению ранга), количество блоков R аппроксимируется количеством ненулевых столбцов в матрице C, размер блоков Lr аппроксимируется количеством ненулевых столбцов в блоках с индексом r в матрицах A и B, соответствующих ненулевым столбцам в C.

При этом рассматривается только модель блочного тензорного разложения размерности (Lr, Lr, 1). Несмотря на то, что данный тип тензорного разложения может быть использован для более общего случая (Ir, Jr, Kr), для задачи мультимодального объединения в визуальных вопросно-ответных системах в настоящее время применяется вычисление для размерности (Lr, Lr, 1), поскольку этого достаточно для систем данного типа.

В работе [13] предлагается видоизмененный способ регуляризации R и Lr:

,

где F(A, B, C) – матрица размера 2×R, вычисляемая следующим образом:

,

где G – матрица факторов A и B размера , вычисляемая следующим образом: G º [AT BT].

Блок с индексом r и размером (I + J) × Lr вычисляется следующим образом:

Данное ограничение позволяет минимизировать число блоков и увеличить разреженность столбцов в оставшихся блоках. Задача решается с помощью алгоритма IRLS [14]. Оба критерия регуляризации были предложены для блочного тензорного разложения размернос-ти (Lr, Lr, 1).

Реализация регуляризованного блочного тензорного разложения в визуальной вопросно-ответной системе

Предлагаемая модель визуальной вопросно-ответной системы основана на системе билинейного объединения, предложенной в [8], с применением механизма визуального внимания, основанного на Faster R-CNN [5]. Векторные представления слов получены с помощью Skip-thought кодировщика [15], при этом вопрос представлен одним вектором. Билинейный механизм объединения состоит из блочного тензорного разложения с применением регуляризации размера блоков и их количества. Диаграмма модели представлена на рисунке 1.

Вычисление блочного тензорного разложения, а также аппроксимации оптимального размера блоков и их количества осуществляется посредством модифицированного алгоритма IRLS, предложенного в [16] и подходящего для минимизации данной функции потерь. Обучение классификатора осуществляется посредством оптимизатора Adam с перекрестной энтропией в качестве функции потерь и примене-нием ранней остановки. Размер мини-пакета составляет 150 элементов. В качестве возможных вариантов для классификатора были выбраны 3 000 ответов, наиболее часто встречающихся в наборе данных. Для обучения системы использовался бутстреппер PyTorch (https://github.com/Cadene/bootstrap.pytorch). Блок-схе­ма разработанного интеллектуального алгоритма обучения представлена на рисунке 2. Алгоритм может быть запущен несколько раз с разным коэффициентом регуляризации с дальнейшим автоматическим выбором модели, имеющей наименьшее значение функции потерь. При этом время обучения нейронных сетей вопросно-ответной системы не увеличивается, так как выбор модели осуществляется до запуска алгоритма обратного распространения. Таким образом, новизна данной модификации заключается в сокращении временных затрат на оптимизацию гиперпараметров блочного тензорного разложения, а также автоматизации данного процесса, снимая необходимость в подборе данных параметров.

Для обучения модели был использован набор данных VQA v2 [17], состоящий из 658 111 элементов обучающей выборки и 447 793 элементов тестового набора. Элементы представляют собой триплеты вида «изображение, вопрос, ответ». Результаты эксперимента приведены в таблице.

Из полученных результатов следует, что система способна находить оптимальные параметры блочного тензорного разложения и дости-гать точности распознавания уровня современных визуальных вопросно-ответных систем, использующих методы тензорного разложения. Дальнейшая работа над увеличением эффективности работы модели может заключаться в улучшении архитектуры нейронных сетей, применяемых в модели, в частности, нелинейных операторов, применяемых в сверточных слоях сети обработки изображений [18], а также в усовершенствовании механизма внимания [19].

Результаты тестирования существующих моделей и предлагаемой модификации на наборе данных VQA v2

Testing results of existing and proposed models on VQA v2 dataset

Заключение

Таким образом, в данной работе был проведен анализ исследований в области тензорного разложения в задачах мультимодального объединения при разработке визуальных вопросно-ответных систем. Отдельное внимание уделено блочному тензорному разложению, так как на момент написания данной работы этот метод показал наибольшую эффективность при снижении размерности в билинейных визуальных вопросно-ответных системах. Была предложена модификация алгоритма обучения, позволяющая более эффективно использовать данный тип тензорного разложения. Разработка визуальных вопросно-ответных систем является относительно новой научной задачей. Вместе с появлением более сложных архитектур глубоких нейронных сетей, а также наборов данных с более широким разнообразием изображений необходима дальнейшая работа над оптимизацией размерности в данных системах.

Литература

1.    Бурхонов Р.А. Сравнительный анализ библиотек для глубокого обучения сверточных нейронных сетей // Сб. тр. VI Междунар. науч. конф. SCVRT2018. 2018. С. 235–240.

2.    Bengio Y. Learning deep architectures for AI. Foundations and Trends in Machine Learning, 2009, vol. 2, no. 1, pp. 1–127. DOI: 10.1561/2200000006.

3.    Фаворская М.Н. Структурные особенности сверточных нейронных сетей для задач распознавания изображений // Сб. тр. XXI Междунар. конф. DSPA. 2019. C. 542–546.

4.    Созыкин А.В. Обзор методов обучения глубоких нейронных сетей // Вестн. Южно-Уральского гос. ун-та. Сер.: Вычислительная математика и информатика. 2017. Т. 6. № 3. С. 28–59. DOI: 10.14529/cmse170303.

5.    Girshick R., Donahue J., Darrell T., Malik J. Rich feature hierarchies for accurate object detection and semantic segmentation. Proc. 27th IEEE Conf. on Computer Visual and Pattern Recognition, 2014, pp. 580–587. DOI: 10.1109/CVPR.2014.81.

6.    Agrawal A., Lu J., Antol S., Mitchell M., Zitnick C.L., Parikh D., Batra D. VQA: Visual Question Answering. IJCV, 2016, vol. 123, no. 1, pp. 4–31. DOI: 10.1007/s11263-016-0966-6.

7.    Charikar M., Chen K., Farach-Colton M. Finding frequent items in data streams. In Automata, Languages and Programming, 2002, pp. 693–703. DOI: 10.1007/3-540-45465-9_59.

8.    Fukui A., Park D.H., Yang D., Rohrbach A., Darrell T., Rohrbach M. Multimodal compact bilinear pooling for visual question answering and visual grounding. Proc. 2016 Conf. on Empirical Methods in Natural Language Processing, 2016, pp. 457–468. DOI: 10.18653/v1/D16-1044.

9.    Kolda T.G., Bader B.W. Tensor decompositions and applications. SIAM Review, 2009, vol. 51, no. 3, pp. 455–500. DOI: 10.1137/07070111X.

10. De Lathauwer L. Decompositions of a higher-order tensor in block terms – Part II: Definitions and uniqueness. SIMAX, 2008, vol. 30, no. 3, pp. 1033–1066. DOI: 10.1137/070690729.

11. Ben-Younes H., Cadene R., Thome N., Cord M. BLOCK: Bilinear superdiagonal fusion for visual question answering and visual relationship detection. Proc. AAAI Conf. on Artificial Intelligence, 2019, vol. 33, pp. 8102–8109. DOI: 10.1609/aaai.v33i01.33018102.

12. De Morais Goulart J.H., de Oliveira P.M.R., Farias R.C., Zarzoso V., Comon P. Alternating group lasso for block-term tensor decomposition with application to ECG source separation. IEEE Transactions on Signal Processing, 2019, vol. 68, pp. 2682–2696. DOI: 10.1109/TSP.2020.2985591.

13. Rontogiannis A.A., Kofidis E., Giampouras P.V. Block-Term Tensor Decomposition: Model Selection and Computation. 2020. URL: https://arxiv.org/abs/2002.09759 (дата обращения: 14.09.2020).

14. Daubechies I., Devore R., Fornasier M., Güntürk C.S. Iteratively reweighted least squares minimization for sparse recovery. Communications on Pure and Applied Mathematics, 2010, vol. 63, no. 1, pp. 1–38. DOI: 10.1002/CPA.20303.

15. Kiros R., Zhu Y., Salakhutdinov R., Zemel R.S., Torralba A., Urtasun R., Fidler S. Skip-thought vectors. Advances in NIPS, 2015, pp. 3294–3302.

16. Giampouras P.V., Rontogiannis A.A., Koutroumbas K.D. Alternating iteratively reweighted least squares minimization for low-rank matrix factorization. IEEE Transactions on Signal Processing, 2019, vol. 67, no. 2, pp. 490–503. DOI: 10.1109/TSP.2018.2883921.

17. Goyal Y., Khot T., Summers-Stay D., Batra D., Parikh D. Making the V in VQA matter: Elevating the role of image understanding in Visual Question Answering. International Journal of Computer Vision, 2018, vol. 127, no. 4, pp. 398–414. DOI: 10.1007/s11263-018-1116-0.

18. Favorskaya M.N., Andreev V.V. The study of activation functions in deep learning for pedestrian detection and tracking. ISPRS, 2019, vol. XLII-2/W12, pp. 53–59. DOI: 10.5194/isprs-archives-XLII-2-W12-53-2019.

19. Favorskaya M., Andreev V., Popov A. Salient region detection in the task of visual question answering. IOP Conf. Series: Materials Science and Engineering, 2018, vol. 450, art. 052017. DOI: 10.1088/1757-899x/450/5/052017.

20. Gao P., Jiang Z., You H., Lu P., Hoi S.C., Wang X., Li H. Dynamic fusion with intra-and inter-modality attention flow for visual question answering. Proc. IEEE Conf. on CVPR, 2019, pp. 6639–6648. DOI: 10.1109/CVPR.2019.00680.

21. Teney D., Anderson P., He X., van den Hengel A. Tips and tricks for visual question answering: Learnings from the 2017 challenge. Proc. IEEE Conf. on CVPR, 2018, pp. 4223–4232. DOI: 10.1109/CVPR.2018.00444.

References

1. Burkhonov R.A. Comparative analysis of libraries for deep learning in convolutional neural networks. Proc. VI Intern. Sci. Conf. SCVRT2018, 2018, pp. 235–240 (in Russ.).
2. Bengio Y. Learning deep architectures for AI. Foundations and Trends in Machine Learning, 2009,
   vol. 2, no. 1, pp. 1–127. DOI: 10.1561/2200000006.
3. Favorskaya M.N. Structured features of convolutional neural networks in the tasks of image recognition. Proc. XXI Intern. Conf. DSPA, 2019, pp. 542–546 (in Russ.).
4. Sozykin A.V. An Overview of methods for deep learning in neural networks. Bull. of the South Ural State University. Ser.: Computational Mathematics and Software Engineering, 2017, vol. 6, no. 3, pp. 28–59 (in Russ.). DOI: 10.14529/cmse170303.
5. Girshick R., Donahue J., Darrell T., Malik J. Rich feature hierarchies for accurate object detection and semantic segmentation. Proc. 27th IEEE Conf. on Computer Visual and Pattern Recognition, 2014,
   pp. 580–587. DOI: 10.1109/CVPR.2014.81.
6. Agrawal A., Lu J., Antol S., Mitchell M., Zitnick C.L., Parikh D., Batra D. VQA: Visual Question Answering. IJCV, 2016, vol. 123, no. 1, pp. 4–31. DOI: 10.1007/s11263-016-0966-6.
7. Charikar M., Chen K., Farach-Colton M. Finding frequent items in data streams. In: Automata, Languages and Programming, 2002, pp. 693–703. DOI: 10.1007/3-540-45465-9_59.
8. Fukui A., Park D.H., Yang D., Rohrbach A., Darrell T., Rohrbach M. Multimodal compact bilinear pooling for visual question answering and visual grounding. Proc. 2016 Conf. on Empirical Methods in Natural Language Processing, 2016, pp. 457–468. DOI: 10.18653/v1/D16-1044.
9. Kolda T.G., Bader B.W. Tensor decompositions and applications. SIAM Review, 2009, vol. 51, no. 3, pp. 455–500. DOI: 10.1137/07070111X.
10. De Lathauwer L. Decompositions of a higher-order tensor in block terms – Part II: Definitions and uniqueness. SIMAX, 2008, vol. 30, no. 3, pp. 1033–1066. DOI: 10.1137/070690729.
11. Ben-Younes H., Cadene R., Thome N., Cord M. BLOCK: bilinear superdiagonal fusion for visual question answering and visual relationship detection. Proc. AAAI Conf. on Artificial Intelligence, 2019,
    vol. 33, pp. 8102–8109. DOI: 10.1609/aaai.v33i01.33018102.
12. De Morais Goulart J.H., de Oliveira P.M.R., Farias R.C., Zarzoso V., Comon P. Alternating group lasso for block-term tensor decomposition with application to ECG source separation. IEEE Transactions on Signal Processing, 2019, vol. 68, pp. 2682–2696. DOI: 10.1109/TSP.2020.2985591.
13. Rontogiannis A.A., Kofidis E., Giampouras P.V. Block-Term Tensor Decomposition: Model Selection and Computation. 2020. Available at: https://arxiv.org/abs/2002.09759 (accessed September 14, 2020).
14. Daubechies I., Devore R., Fornasier M., Güntürk C.S. Iteratively reweighted least squares minimization for sparse recovery. Communications on Pure and Applied Mathematics, 2010, vol. 63, no. 1, pp. 1–38. DOI: 10.1002/CPA.20303.
15. Kiros R., Zhu Y., Salakhutdinov R., Zemel R.S., Torralba A., Urtasun R., Fidler S. Skip-Thought Vectors. Advances in NIPS, 2015, pp. 3294–3302.
16. Giampouras P.V., Rontogiannis A.A., Koutroumbas K.D. Alternating iteratively reweighted least squares minimization for low-rank matrix factorization. IEEE Transactions on Signal Processing, 2019,
    vol. 67, no. 2, pp. 490–503. DOI: 10.1109/TSP.2018.2883921.
17. Goyal Y., Khot T., Summers-Stay D., Batra D., Parikh D. Making the V in VQA matter: Elevating the role of image understanding in Visual Question Answering. International Journal of Computer Vision, 2018, vol. 127, no. 4, pp. 398–414. DOI: 10.1007/s11263-018-1116-0.
18. Favorskaya M.N., Andreev V.V. The study of activation functions in deep learning for pedestrian detection and tracking. ISPRS, 2019, vol. XLII-2/W12, pp. 53–59. DOI: 10.5194/isprs-archives-XLII-2-W12-53-2019.
19. Favorskaya M., Andreev V., Popov A. Salient region detection in the task of visual question answering. IOP Conf. Series: Materials Science and Engineering, 2018, vol. 450, art. 052017. DOI: 10.1088/1757-899x/450/5/052017.
20. Gao P., Jiang Z., You H., Lu P., Hoi S.C., Wang X., Li H. Dynamic fusion with intra-and inter-modality attention flow for visual question answering. Proc. IEEE Conf. on CVPR, 2019, pp. 6639–6648. DOI: 10.1109/CVPR.2019.00680.
21. Teney D., Anderson P., He X., van den Hengel A. Tips and tricks for visual question answering: Learnings from the 2017 challenge. Proc. IEEE Conf. on CVPR, 2018, pp. 4223–4232. DOI: 10.1109/CVPR.
    2018.00444.