При построении систем классификации объектов, характеризующихся разнотипными (количественными и качественными) признаками, наибольшее распространение получили следующие методы:
- логические, использующие методы бинарной (четкой) логики;
- логические, использующие методы нечеткой или размытой логики;
- нейросетевые.
Наряду с известными достоинствами все эти методы имеют определенные недостатки. Так, логические бинарные алгоритмы классификации отличаются очень длительной, не всегда сходящейся процедурой обучения, нейросетевые не учитывают имеющуюся априорную информацию и, как правило, требуют очень большую обучающую выборку. Алгоритмы, использующие аппарат нечеткой логики, существенным образом зависят от параметров, полноты и непротиворечивости исходного набора постулируемых нечетких правил, формулируемых экспертом человеком и т.д.
Весьма перспективными в этом аспекте являются гибридные или комбинированные нейро-нечеткие методы [1,2], один из которых изложен ниже.
 Для конкретизации задачи исследования уточним прежде всего объем имеющейся предварительной (априорной) информации.
Для конкретизации задачи исследования уточним прежде всего объем имеющейся предварительной (априорной) информации.
1. Будем полагать, что часть признаков объекта носит количественный характер, а часть качественный; данные признаки, вообще говоря, изменяются от объекта к объекту, даже при принадлежности объектов к одному классу, но о вероятностной природе этих признаков сказать ничего нельзя. Области значений  всех переменных полагаются известными. Кроме этого, предполагается заданной следующая априорная информация.
всех переменных полагаются известными. Кроме этого, предполагается заданной следующая априорная информация.
2. Известно общее число распознаваемых образов S, но априорные вероятности принадлежности объекта к тому или иному образу неизвестны.
3. Приблизительные соотношения между переменными (признаками) в форме высказываний "если-то", позволяющие относить (ориентировочно) объект с произвольным вектором признаков x к одному из классов.
4. Имеется обучающая выборка данных.
Основную идею предлагаемого метода поясним следующим образом.
Предположим вначале, что все признаки  являются количественными, а рассматриваемые объекты принадлежат к одному из двух классов (то есть S=2), при этом данные объекты принадлежат линейно разделимым множествам. Такая ситуация при наличии только двух признаков (
являются количественными, а рассматриваемые объекты принадлежат к одному из двух классов (то есть S=2), при этом данные объекты принадлежат линейно разделимым множествам. Такая ситуация при наличии только двух признаков ( и
и  ) отображена на рисунке 1.
) отображена на рисунке 1.
Пусть для данной ситуации
 , (1)
, (1)
где

 (2)
(2)
является уравнением некоторой прямой, разделяющей объекты разных классов.
Тогда решающее правило классификации может быть записано как
 (3)
(3)
Очевидно, подобное решающее правило остается в силе при наличии n признаков, то есть при 
В случае S образов можно предложить следующее решающее правило
П:  если
если  , (4)
, (4)
где  – линейные формы вида
– линейные формы вида


 (5)
(5)
Теперь предположим, что признаки являются качественными, и их значения для конкретных условий можно отразить значениями принадлежности  к некоторым нечетким множествам. Возвращаясь к примеру с n=2 и используя вместо операции умножения логическую операцию
к некоторым нечетким множествам. Возвращаясь к примеру с n=2 и используя вместо операции умножения логическую операцию  (определения минимума, min), а вместо операции сложения – V (определение максимума, max), для принадлежности переменной вывода можно записать:
(определения минимума, min), а вместо операции сложения – V (определение максимума, max), для принадлежности переменной вывода можно записать:
 , (6)
, (6)
где, очевидно, необходимо выполнение ограничений

 (7)
(7)
Решающее правило в этом случае принимает вид:
 если
если  то
то  ,
,
иначе 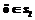 . (8)
. (8)
В общем случае априорная информация должна быть представлена в форме:
 V
V ,
,
 V
V ,
,
. . .
 V
V ,
,
или в более сокращенной записи:


 ,
,

 ,
, (9)
(9)
при этом правило классификации описывается выражением

 , если
, если  . (10)
. (10)
Очевидно, здесь  следует трактовать как уровень принадлежности предъявленного объекта классу
следует трактовать как уровень принадлежности предъявленного объекта классу  ,
,  – некоторые постоянные коэффициенты, а смысловое значение
– некоторые постоянные коэффициенты, а смысловое значение  было пояснено ранее.
было пояснено ранее.
Между тем, используя понятия нечеткого отношения и max-min композиции нечетких отношений [1, 2], запись (9) может быть представлена как векторно-матричное соотношение:
Г=R · M, (11)
где
Г =  , (12)
, (12)
R =  , (13)
, (13)
М =  , (14)
, (14)
а "·" – символ max-min композиции (max-min свертки) нечетких выводов, при этом коэффициенты  будут характеризовать некоторые причинные отношения
будут характеризовать некоторые причинные отношения
 (15)
(15)
отражающие знания эксперта.
Нетрудно видеть, что приведенные выкладки справедливы и в случае, если часть переменных-признаков носит количественный характер, достаточно лишь определить для них соответствующие функции принадлежности  (и необходимым образом сформулировать матрицу R).
(и необходимым образом сформулировать матрицу R).
С учетом введенных обозначений решающее правило можно записать так:

 , если
, если  /Г=R·М (16)
/Г=R·М (16)
(матричное соотношение после косой черты указывает на условие, накладываемое на вектор Г).
Отметим, что содержательная трактовка соотношений (9) отображается утверждениями вида:
если  есть
есть  или
или  есть
есть  или … или
или … или  есть
есть  , то х
, то х
с принадлежностью  , определяемой (9), при этом
, определяемой (9), при этом 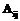 – некоторые нечеткие множества с принадлежностями
– некоторые нечеткие множества с принадлежностями  .
.
Однако часто знания экспертов формируются как утверждения:
если  есть
есть  и
и  есть
есть  и … и
и … и  есть
есть  , то х
, то х с принадлежностью
с принадлежностью  .
.
Как легко показать, соотношения (11)-(14), (16) здесь считаются в силе, но при использовании min-max композиции нечетких отношений, при которой
 . (17)
. (17)
В наиболее общем случае целесообразно использовать понятие операции композиции, определяемой через t-норму и t-конорму [2,3].
Приведенные математические выкладки позволяют теперь пояснить основную идею предлагаемого метода. Сущность его заключается в использовании для классификации решающего правила (16) с корректировкой элементов матрицы R на основе имеющихся экспериментальных данных, то есть обучающей выборки. Элементы же матрицы М (см. (14)), то есть принадлежности и функции принадлежности переменных-признаков, считаются заданными априори (на основании знания экспертов) и их дальнейшая корректировка не предполагается.
Реализация соотношений, например, вида (17), (11)-(14) с помощью нечетких нейронов "И", в общем виде реализует соотношение
 . (18)
. (18)
Здесь слой нечетких нейронов образован нечеткими нейронами типа "И", на входы которых с некоторыми "весами"  поступают введенные выше принадлежности
поступают введенные выше принадлежности  ; входы нейронов
; входы нейронов  являются мерами принадлежности предъявленного объекта
являются мерами принадлежности предъявленного объекта  к классу s1, s2,…, sS соответственно.
к классу s1, s2,…, sS соответственно.
Заметим, что точно такой же структурой отображаются и соотношения (9), (11)-(14), только в качестве нейронов в этом случае должны быть использованы нечеткие нейроны "ИЛИ".
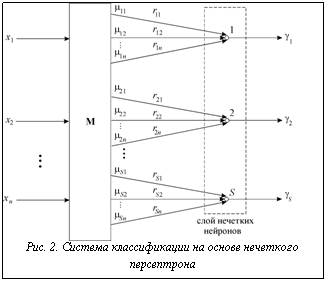 Приведенная на рисунке 2 система классификации реализует предложенный метод, при этом слой нечетких нейронов (вместе со своими входами, выходами и весами) образует так называемый нечеткий персептрон [2]. Учитывая данное обстоятельство, для уточнения элементов
Приведенная на рисунке 2 система классификации реализует предложенный метод, при этом слой нечетких нейронов (вместе со своими входами, выходами и весами) образует так называемый нечеткий персептрон [2]. Учитывая данное обстоятельство, для уточнения элементов  (весов персептрона) можно воспользоваться следующим соотношением:
(весов персептрона) можно воспользоваться следующим соотношением:
r r
r m
m (19)
(19)
где t – текущий такт обучения; r – вектор весовых коэффициентов i-го нейрона; h – коэффициент скорости обучения, 0 – желаемый вход i-го нейрона при предъявлении на вход системы объекта с вектором признаков x
– вектор весовых коэффициентов i-го нейрона; h – коэффициент скорости обучения, 0 – желаемый вход i-го нейрона при предъявлении на вход системы объекта с вектором признаков x ;
;  – фактический выход i-го нейрона;
– фактический выход i-го нейрона;
m
 – вектор входов i-го нейрона, формируемый в соответствии с известным предъявленным вектором x
– вектор входов i-го нейрона, формируемый в соответствии с известным предъявленным вектором x .
.
Здесь m (x
(x ) рассчитывается по известной матрице М (определяемой соотношением (19)), а значения
) рассчитывается по известной матрице М (определяемой соотношением (19)), а значения  берутся из обучающей выборки. Формула (19) соответствует дельта-правилу обычного ("четкого") персептрона, при этом алгоритм построения и обучения системы классификации вида, представленного на рисунке 2, может быть описан следующим образом.
берутся из обучающей выборки. Формула (19) соответствует дельта-правилу обычного ("четкого") персептрона, при этом алгоритм построения и обучения системы классификации вида, представленного на рисунке 2, может быть описан следующим образом.
1. Определяется совокупность  признаков классифицируемых объектов и множество имен s1¸sS рассматриваемых классов.
признаков классифицируемых объектов и множество имен s1¸sS рассматриваемых классов.
2. Формируется обучающая выборка.
3. Экспертным путем определяются (задаются) элементы матрицы М – то есть функции принадлежности  для количественных признаков и правила нахождения степеней принадлежности для качественных признаков.
для количественных признаков и правила нахождения степеней принадлежности для качественных признаков.
4. Экспертным путем, если это возможно, на основании продукционных правил ЕСЛИ-ТО задаются начальные значения  элементов матрицы R, то есть начальные значения весов нечеткого персептрона.
элементов матрицы R, то есть начальные значения весов нечеткого персептрона.
В противном случае элементы данной матрицы инициируются небольшими случайными положительными значениями (меньшими единицы).
5. На вход системы подается один из входных векторов x образующей выборки и в соответствии с формулой (16) вычисляется ее выход.
образующей выборки и в соответствии с формулой (16) вычисляется ее выход.
6. Если выход правильный, то осуществляется переход на шаг 7. Иначе – вычисляется разница между идеальными  и полученными значениями выходов нейронов:
и полученными значениями выходов нейронов:

 (20)
(20)
и модифицируются веса в соответствии с формулой
 (21)
(21)
при учете ограничений
 (22)
(22)
7. Организуется цикл с шага 5 до выполнения правила останова обучения. В качестве такого правила может быть, например, использовано выполнение неравенства
 ош
ош (23)
(23)
где  – некоторое малое неотрицательное число (
– некоторое малое неотрицательное число ( или
или  и т.д.), характеризующее качество работы системы (заданную вероятность ошибочной классификации);
и т.д.), характеризующее качество работы системы (заданную вероятность ошибочной классификации);  число объектов i-го класса в обучающей выборке,
число объектов i-го класса в обучающей выборке, 
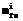 – число ошибочно классифицированных объектов i-го класса обучающей выборки;
– число ошибочно классифицированных объектов i-го класса обучающей выборки;  ош – оценка вероятности ошибочной классификации.
ош – оценка вероятности ошибочной классификации.
Учитывая известные результаты по сходимости процедур обучения персептронов и теорему о полноте для систем нечеткого вывода [2], можно полагать, что предложенный алгоритм обеспечит построение системы, дающей безошибочную классификацию, по крайней мере для линейно разделимых множеств объектов (в координатах  ). Возможность такой классификации в случае нелинейных разделяющих поверхностей с помощью рассмотренной структуры представляется неясной, при этом усложнение системы за счет введения дополнительных слоев нечетких нейронов выигрыша не дает.
). Возможность такой классификации в случае нелинейных разделяющих поверхностей с помощью рассмотренной структуры представляется неясной, при этом усложнение системы за счет введения дополнительных слоев нечетких нейронов выигрыша не дает.
По-видимому, более перспективным в смысле повышения качества функционирования системы классификации является задание числа Q нечетких нейронов существенно большим, чем число классов S, то есть
Q > S, (24)
при этом не один, а одновременно несколько таких нейронов ассоциируются с одним из образов  . Отметим, что в данном случае сохраняют силу как решающее правило (16), так и описанный алгоритм построения и обучения системы.
. Отметим, что в данном случае сохраняют силу как решающее правило (16), так и описанный алгоритм построения и обучения системы.
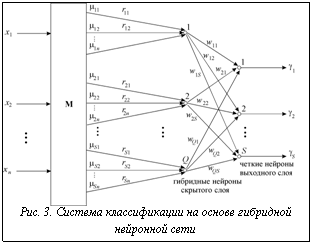
Как представляется, еще большими возможностями будет обладать реализация метода классификации на базе гибридной (нечеткой) нейронной сети, содержащей как нечеткие, так и "четкие" нейроны с сигмоидальной активационной функцией.
Структура системы классификации на основе гибридной нейронной сети приведена на рисунке 3.
Здесь гибридные нейроны скрытого слоя описываются соотношениями
 (25)
(25)
 (26)
(26)
или

 ,
,  , (27)
, (27)
а четкие нейроны выходного слоя – соотношениями
 (28)
(28)
где w – вектор весовых коэффициентов m-го выходного нейрона; b
– вектор весовых коэффициентов m-го выходного нейрона; b – вектор выходов нечетких нейронов скрытого слоя.
– вектор выходов нечетких нейронов скрытого слоя.
Таким образом, в нейронах как скрытого, так и выходного слоя используются сигмоидальные (логистические) функции активации [2] с областью значений, принадлежащих отрезку [0,1].
Решение об отнесении предъявленного объекта к какому-либо классу выглядит аналогично ранее приведенному (10), а процедура определения весов r w
w основывается на следующих выкладках и предположениях:
основывается на следующих выкладках и предположениях:
1) начальные значения векторов r устанавливаются с учетом имеющейся априорной информации;
устанавливаются с учетом имеющейся априорной информации;
2) в качестве начальных значений элементов векторов w задаются малые (много меньше единицы) случайные величины;
задаются малые (много меньше единицы) случайные величины;
3) коррекция элементов r и w
и w осуществляется методом обратного распространения [2].
осуществляется методом обратного распространения [2].
В качестве функции ошибки для k-го предъявленного объекта примем величину
 (29)
(29)
Соответственно, суммарная функция ошибки по всем примерам обучающей выборки
 (30)
(30)
Очевидно, как  , так и Е являются функциями векторов весов сети r
, так и Е являются функциями векторов весов сети r , w
, w . Задача обучения сети сводится в данном случае к подбору таких векторов r
. Задача обучения сети сводится в данном случае к подбору таких векторов r и w
и w (
( ,
,  ), при котором достигается минимум Е.
), при котором достигается минимум Е.
Данную задачу будем решать градиентным методом, используя соотношения
w w
w w
w (31)
(31)
r r
r r
r (32)
(32)
где “:=” – символ оператора присвоения;  w
w и
и  r
r – обозначения векторов-градиентов; h – коэффициент скорости обучения (0
– обозначения векторов-градиентов; h – коэффициент скорости обучения (0
Полагая константу h заданной, для детализации правых частей (31), (32) найдем выражения для векторов-градиентов.
Очевидно, на основании (29) имеем:
 w
w
 w
w . (33)
. (33)
Используя далее формулу (28) и известное соотношение для производной сигмоидальной логистической функции, получим
 w
w
 b
b (34)
(34)
и окончательно
 w
w
 b
b . (35)
. (35)
Поступая аналогично для нахождения  r
r и используя соотношения (29), (27), (25), свойство производной сигмоидальной функции и цепное правило дифференцирования для сложной функции, будем иметь:
и используя соотношения (29), (27), (25), свойство производной сигмоидальной функции и цепное правило дифференцирования для сложной функции, будем иметь:
 r
r
 . (36)
. (36)
В данном случае
 , (37)
, (37)
 . (38)
. (38)
Вектор-градиент  r
r находится на основании следующих рассуждений. Пусть, например,
находится на основании следующих рассуждений. Пусть, например,  определяется на основании равенства (26), то есть
определяется на основании равенства (26), то есть
 , (39)
, (39)
где 
Очевидно, небольшие вариации коэффициента  не приведут к изменению
не приведут к изменению  , если только составляющая
, если только составляющая  не является наименьшей по сравнению с другими такими составляющими в правой части (39). Если же данная составляющая является наименьшей, но
не является наименьшей по сравнению с другими такими составляющими в правой части (39). Если же данная составляющая является наименьшей, но  , изменение
, изменение  при вариациях
при вариациях  тоже будет равно нулю.
тоже будет равно нулю.
При  и при вариациях
и при вариациях  для данной (наименьшей) составляющей
для данной (наименьшей) составляющей
 . (40)
. (40)
Однако это неравенство будет оставаться справедливым только до тех пор, пока отмечен- ная составляющая продолжит оставаться наименьшей.
Если наименьшими одновременно являются несколько составляющих, то ситуация, вообще говоря, является неопределенной.
Изложенное позволяет записать:
1)  если для всех
если для всех  справедливо
справедливо
 (41)
(41)
(то есть в этом случае все элементы рассматриваемого вектора-градиента равны нулю);
2) если для наименьшей составляющей вида  справедливо неравенство
справедливо неравенство
 , (42)
, (42)
то соответствующий элемент
 (43)
(43)
а остальные элементы вектора  равны нулю;
равны нулю;
3) если в выражении (39) для  одновременно несколько составляющих являются наименьшими, при этом для некоторых из них выполняется условие (42), то для исключения неопределенности одно из них можно (случайным образом, например) положить "самым наименьшим" и принять, что для него справедливо (43).
одновременно несколько составляющих являются наименьшими, при этом для некоторых из них выполняется условие (42), то для исключения неопределенности одно из них можно (случайным образом, например) положить "самым наименьшим" и принять, что для него справедливо (43).
Таким образом, вектор  является либо нулевым, то есть
является либо нулевым, то есть
 , (44)
, (44)
либо имеет только один ненулевой элемент, равный единице, то есть
 . (45)
. (45)
Рассуждая аналогично при использовании соотношения (27), получим, что и для такой ситуации  будет иметь вид либо (44), либо (45), причем ненулевой элемент соответствует максимальной составляющей формы в правой части (27) при условии, что для нее
будет иметь вид либо (44), либо (45), причем ненулевой элемент соответствует максимальной составляющей формы в правой части (27) при условии, что для нее
 . (46)
. (46)
Полученные выкладки позволяют теперь описать весь алгоритм построения и обучения системы классификации на базе гибридной нейронной сети.
1. Определяется совокупность  признаков классифицируемых объектов и множество имен
признаков классифицируемых объектов и множество имен  рассматриваемых классов.
рассматриваемых классов.
2. Формируется обучающая выборка вида.
3. Экспертным путем определяются (задаются) элементы матрицы М – то есть функции принадлежности  для количественных признаков и правила нахождения степеней принадлежности для качественных признаков.
для количественных признаков и правила нахождения степеней принадлежности для качественных признаков.
4. Экспертным путем на основании продукционных правил ЕСЛИ-ТО задаются начальные значения  элементов матрицы R. Если соответствующая априорная информация отсутствует, элементы данной матрицы инициируются небольшими случайными положительными значениями (меньшими единицы).
элементов матрицы R. Если соответствующая априорная информация отсутствует, элементы данной матрицы инициируются небольшими случайными положительными значениями (меньшими единицы).
5. Задаются начальные значения (малые случайные числа) элементов векторов  .
.
6. На вход системы подается один из входных векторов  обучающей выборки и в соответствии с соотношениями (25), (26) (или (27)), (28), (29) рассчитывается выход системы. Если выход правильный, то осуществляется переход к шагу 7 алгоритма. Иначе – осуществляется коррекция весов сети:
обучающей выборки и в соответствии с соотношениями (25), (26) (или (27)), (28), (29) рассчитывается выход системы. Если выход правильный, то осуществляется переход к шагу 7 алгоритма. Иначе – осуществляется коррекция весов сети:
 , (47)
, (47)
 , (48)
, (48)
 ,
,
где вектор-градиент  определяется одним из соотношений – (44) или (45) – в зависимости от условий (41), (32) (или (46), (43)).
определяется одним из соотношений – (44) или (45) – в зависимости от условий (41), (32) (или (46), (43)).
7. Организуется цикл с шага 6 до выполнения правила останова обучения. В качестве такого правила может быть использовано, например, выполнение неравенства (23).
Список литературы
1. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. - М.: Физматлит, 2001.
2. Круглов В.В., Дли М.И. Интеллектуальные информационные системы: компьютерная реализация систем нечеткой логики и нечеткого вывода. - М.: Физматлит, 2002.
3. Комарцова Л.Г., Максимов А.В. Нейрокомпьютеры. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.




 всех переменных полагаются известными. Кроме этого, предполагается заданной следующая априорная информация.
всех переменных полагаются известными. Кроме этого, предполагается заданной следующая априорная информация. являются количественными, а рассматриваемые объекты принадлежат к одному из двух классов (то есть S=2), при этом данные объекты принадлежат линейно разделимым множествам. Такая ситуация при наличии только двух признаков (
являются количественными, а рассматриваемые объекты принадлежат к одному из двух классов (то есть S=2), при этом данные объекты принадлежат линейно разделимым множествам. Такая ситуация при наличии только двух признаков ( и
и  ) отображена на рисунке 1.
) отображена на рисунке 1. , (1)
, (1)
 (2)
(2) (3)
(3)
 если
если  , (4)
, (4) – линейные формы вида
– линейные формы вида

 (5)
(5) к некоторым нечетким множествам. Возвращаясь к примеру с n=2 и используя вместо операции умножения логическую операцию
к некоторым нечетким множествам. Возвращаясь к примеру с n=2 и используя вместо операции умножения логическую операцию  (определения минимума, min), а вместо операции сложения – V (определение максимума, max), для принадлежности переменной вывода можно записать:
(определения минимума, min), а вместо операции сложения – V (определение максимума, max), для принадлежности переменной вывода можно записать: , (6)
, (6)
 (7)
(7) если
если  то
то  ,
,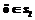 . (8)
. (8) V
V ,
, V
V ,
, V
V ,
,

 ,
, ,
, (9)
(9) , если
, если  . (10)
. (10) следует трактовать как уровень принадлежности предъявленного объекта классу
следует трактовать как уровень принадлежности предъявленного объекта классу  ,
,  – некоторые постоянные коэффициенты, а смысловое значение
– некоторые постоянные коэффициенты, а смысловое значение  было пояснено ранее.
было пояснено ранее. , (12)
, (12) , (13)
, (13) , (14)
, (14) (15)
(15) или
или  или … или
или … или  есть
есть  , то х
, то х
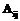 – некоторые нечеткие множества с принадлежностями
– некоторые нечеткие множества с принадлежностями  .
. . (17)
. (17) . (18)
. (18) ; входы нейронов
; входы нейронов  являются мерами принадлежности предъявленного объекта
являются мерами принадлежности предъявленного объекта  к классу s1, s2,…, sS соответственно.
к классу s1, s2,…, sS соответственно. Приведенная на рисунке 2 система классификации реализует предложенный метод, при этом слой нечетких нейронов (вместе со своими входами, выходами и весами) образует так называемый нечеткий персептрон [2]. Учитывая данное обстоятельство, для уточнения элементов
Приведенная на рисунке 2 система классификации реализует предложенный метод, при этом слой нечетких нейронов (вместе со своими входами, выходами и весами) образует так называемый нечеткий персептрон [2]. Учитывая данное обстоятельство, для уточнения элементов  r
r m
m (19)
(19) – вектор весовых коэффициентов i-го нейрона; h – коэффициент скорости обучения, 0 – желаемый вход i-го нейрона при предъявлении на вход системы объекта с вектором признаков x
– вектор весовых коэффициентов i-го нейрона; h – коэффициент скорости обучения, 0 – желаемый вход i-го нейрона при предъявлении на вход системы объекта с вектором признаков x ;
;  – фактический выход i-го нейрона;
– фактический выход i-го нейрона;
 – вектор входов i-го нейрона, формируемый в соответствии с известным предъявленным вектором x
– вектор входов i-го нейрона, формируемый в соответствии с известным предъявленным вектором x берутся из обучающей выборки. Формула (19) соответствует дельта-правилу обычного ("четкого") персептрона, при этом алгоритм построения и обучения системы классификации вида, представленного на рисунке 2, может быть описан следующим образом.
берутся из обучающей выборки. Формула (19) соответствует дельта-правилу обычного ("четкого") персептрона, при этом алгоритм построения и обучения системы классификации вида, представленного на рисунке 2, может быть описан следующим образом.
 (20)
(20) (21)
(21) (22)
(22) ош
ош (23)
(23) – некоторое малое неотрицательное число (
– некоторое малое неотрицательное число ( или
или  и т.д.), характеризующее качество работы системы (заданную вероятность ошибочной классификации);
и т.д.), характеризующее качество работы системы (заданную вероятность ошибочной классификации);  число объектов i-го класса в обучающей выборке,
число объектов i-го класса в обучающей выборке, 
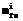 – число ошибочно классифицированных объектов i-го класса обучающей выборки;
– число ошибочно классифицированных объектов i-го класса обучающей выборки;  (25)
(25) (26)
(26)
 ,
,  (28)
(28) – вектор весовых коэффициентов m-го выходного нейрона; b
– вектор весовых коэффициентов m-го выходного нейрона; b – вектор выходов нечетких нейронов скрытого слоя.
– вектор выходов нечетких нейронов скрытого слоя. w
w основывается на следующих выкладках и предположениях:
основывается на следующих выкладках и предположениях: устанавливаются с учетом имеющейся априорной информации;
устанавливаются с учетом имеющейся априорной информации; задаются малые (много меньше единицы) случайные величины;
задаются малые (много меньше единицы) случайные величины; (29)
(29)
 (30)
(30) , так и Е являются функциями векторов весов сети r
, так и Е являются функциями векторов весов сети r ,
,  ), при котором достигается минимум Е.
), при котором достигается минимум Е. w
w w
w (31)
(31) r
r r
r (32)
(32) w
w w
w w
w b
b b
b . (36)
. (36) , (37)
, (37) . (38)
. (38) r
r определяется на основании равенства (26), то есть
определяется на основании равенства (26), то есть , (39)
, (39)
 не является наименьшей по сравнению с другими такими составляющими в правой части (39). Если же данная составляющая является наименьшей, но
не является наименьшей по сравнению с другими такими составляющими в правой части (39). Если же данная составляющая является наименьшей, но  , изменение
, изменение  и при вариациях
и при вариациях  . (40)
. (40) если для всех
если для всех  (41)
(41) (43)
(43) равны нулю;
равны нулю; , (44)
, (44) . (45)
. (45) рассматриваемых классов.
рассматриваемых классов. .
. обучающей выборки и в соответствии с соотношениями (25), (26) (или (27)), (28), (29) рассчитывается выход системы. Если выход правильный, то осуществляется переход к шагу 7 алгоритма. Иначе – осуществляется коррекция весов сети:
обучающей выборки и в соответствии с соотношениями (25), (26) (или (27)), (28), (29) рассчитывается выход системы. Если выход правильный, то осуществляется переход к шагу 7 алгоритма. Иначе – осуществляется коррекция весов сети: , (47)
, (47) , (48)
, (48) ,
,