Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оценка эффективности программных методов обработки изображений
Аннотация:
Abstract:
| Авторы: Самойлин Е.А. (es977@mail.ru) - Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия им. проф. Н.Е. Жуковского и Ю.А. Гагарина» (профессор), Воронеж, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15785 |
Версия для печати Выпуск в формате PDF (1.06Мб) |
Обработка изображений стала одной из наиболее актуальных проблем, в рамках которой решается множество фундаментальных и прикладных задач. Широко распространенные пакеты прикладных программ (MATLAB, MATHCAD и др.) имеют в своем составе самостоятельные модули, позволяющие программно обрабатывать цифровые изображения. Обработка изображений в различных программных системах осуществляется в два основных этапа: предварительная обработка и анализ (распознавание). На этапе предварительной обработки решаются такие задачи, как фильтрация (то есть подавление шумов, помех) и сегментация (то есть выделение контурных линий и информативных признаков). Известно достаточно много методов фильтрации и сегментации изображений [1-11]. Столь широкое их многообразие определяется различными факторами возникновения шумов и помех, а также формами представления изображений. Например, известно [2, 3], что для фильтрации белого гауссовского шума наиболее подходят линейная или нелинейная медианная фильтрация, для подавления низкочастотной составляющей шума эффективны спектральные методы и вейвлет-преобразования [2], для фильтрации высокочастотной составляющей – цифровые фильтры [1], фильтрации фона – согласованные и винеровские фильтры [4] и т.д. При всем многообразии новых методов обработки возникает проблема выбора решения для конкретной задачи, так как в большинстве случаев алгоритмы моделируются на простейших тестовых изображениях, и оценка их проводится визуально. Например, в [5] представлены результаты модифицированной медианной фильтрации на примере тестовых прямоугольников и треугольников, пятен произвольной формы, а также карт облачности, но нет строгой количественной оценки полученных результатов. В работе [6] приведены результаты моделирования пространственной фильтрации-сегментации без их математической оценки. В [7] также графически приведены результаты фильтрации-сегментации простейших тестовых изображений однослойной нейронной сетью без численного анализа. Строгая математическая оценка результатов обработки по предлагаемым алгоритмам отсутствует и в [8-10]. Таким образом, при всем многообразии новых методов фильтрации и сегментации изображений отсутствует строгий математический аппарат оценки их качества. Цель работы – обоснование необходимости введения и выбор универсального целевого функционала для строгой математической оценки эффективности программных методов обработки изображений. Рассмотрим задачу поиска комплексного целевого функционала для расчета многокри- териального показателя, объективно отражающего качество принципиально различных методов и алгоритмов фильтрации-сегментации изображений. Количество критериев оценки должно соответствовать факторам возникновения шумов и помех, а также основным формам представления и описания изображений. Наиболее общими способами описания являются векторно-матричное представление и представление с использованием детерминированных или стохастических функций, а также на их основе структурное, признаковое и множественное представления [11]. Качество различных методов и алгоритмов целесообразно оценивать мерой близости (схожести) вектора изображения в k-мерном пространстве после фильтрации-сегментации с некоторым идеализированным (эталонным) вектором, который должен быть получен в результате идеального алгоритма. Размерность пространства Выбор целевого функционала Шумы и помехи на изображениях могут быть отнесены к одному из факторов возникновения, кроме того, сами изображения характеризуются многообразием форм их представления и описания. Например, в работе [11] предложено классифицировать методы обработки изображений в соответствии с законом описания их характеристик. Исходя из этого искомый комплексный целевой функционал может быть записан в виде матрицы определенной размерности, число элементов вектор-столбцов которой будут соответствовать количеству оцениваемых методов обработки, а число элементов вектор-строк – количеству целевых функций (для расчета отдельных критериев) в зависимости от факторов возникновения шумов и способов описания изображений. Так, оценить эффективность фильтрации-сегментации в условиях белого гауссовского шума для векторно-матричного представления изображений можно путем определения дисперсии многомерных векторов изображений в k-мерном пространстве [3]. При этом вектор-столбец (транспонированная вектор-строка) дисперсии векторов изображений будет иметь вид:
где
Для оценки в условиях фильтрации низкочастотного шума и детерминированным представлением изображений оптимальным будет определение величины расстояния в k-мерном пространстве непрерывных функций с квадратичной метрикой. При этом второй вектор-столбец (строка) примет вид:
где Фильтрация-сегментация при высокочастотном шуме, которая осуществляется цифровыми фильтрами [2] (как правило, в векторно-матричной форме изображений), оценима нахождением величины евклидова расстояния и угла между интересуемыми векторами в k-мерном пространстве. Вектор-столбец (строка) евклидовых расстояний примет вид [12]:
где
Вектор-столбец (строка) угла между векторами примет вид:
Оценка методов при фильтрации текстурных помех и представлении изображений стохастическими функциями осуществима определением степени тесноты линейной зависимости между функциями, что возможно путем вычисления коэффициента взаимной корреляции случайных векторов. Вектор-столбец (строка) будет определяться в соответствии с выражением:
где Оценка методов обработки изображений Для примера с использованием выбранного комплексного целевого функционала, оценена эффективность двух различных методов фильтрации-сегментации полутоновых изображений, то есть N=2. Первый является классической медианной фильтрацией, которая достаточно эффективна при сглаживании белого гауссовского шума [3]. Второй базируется на применении однослойной нейронной сети, сущность которого изложе- на в [7]. Данными методами производилась обработка исходного тестового изображения размерностью 150´200 элементов, показанного на рисунке 1a, с ''зашумленной'' буквой ''А''. Эталонным изображением для тестового (рис. 1a) будет являться показанное на рисунке 1b той же размерности. Изображение, полученное обработкой по методу медианной фильтрации [3], показано на рисунке 2a, а изображение, полученное на выходе однослойной нейронной сети [7] – на рисунке 2b. Для оценки эффективности методов в соответствии с выражениями (1-5) проведен расчет комплексного целевого функционала. Результаты приведены в форме, соответствующей (1-5):
Первая вектор-строка матрицы представляет собой нормированные на себя критериальные показатели (1-5), то есть несоответствие исходного изображения (рис. 1a) с эталонным (рис. 1b); вторая – критериальные показатели ошибки медианной фильтрации-сегментации [3] исходного изображения (рис. 2a); третья – показатели ошибки нейросетевого метода [7] фильтрации-сегментации (рис. 2b). Для удобства анализа результатов представим матрицу его значений графичес- ки (рис. 3).
Таким образом, предложенный универсальный комплексный целевой функционал позволяет проводить строгую многокритериальную оценку эффективности самых различных методов обработки изображений. Согласно полученной математической оценке даже единственный алгоритм фильтрации и сегментации характеризуется различной эффективностью по отношению к факторам возникновения шумов и формам представления изображений. Список литературы 1. Введение в контурный анализ и его приложения к обработке изображений и сигналов. / Под ред. Я.А. Фурмана. – М.: Физматлит, 2002. – 592 с. 2. Панин С.В., Шакиров И.В., Сырямкин В.И., Светла- ков А.А. Применение вейвлет-анализа изображений поверхности для изучения процессов пластической деформации и разрушения на мезомасштабном уровне // Автометрия. 2003. - Т. 39. - № 1. - С. 37-53. 3. Huang T.S. (ed.), Eklundh J.-O., Justusson B.I., Nussbaumer H.J., Tyan S.G., Zohar S. Two-Dimensional Digital Signal Processing II: Transforms and Median Filters (Sprinder-Verlag, Berlin, Heidelberg, New York 1981). 4. Касперович А.Н. Фильтрация, обнаружение и локализация малоразмерных объектов, полученных при круговом субписельном сканировании изображений // Автометрия. - 2002. - Т. 38. - № 5. - С. 17-29.
6. Клочко В.К., Ермаков А.А. Алгоритмы фильтрации и сегментации трехмерных радиолокационных изображений поверхности // Там же. С. 41-48. 7. Серпенинов О.В., Самойлин Е.А., Банников А.В. Нейропрограммный алгоритм предварительной обработки изображений в условиях шумов // Программные продукты и системы. - 2003. - № 2. - С. 17-19. 8. Бессарабов И.И. Использование ориентационной сегментации контуров с целью описания объектов на изображении в терминах отрезков // Автометрия. - 2002. - № 2. - С. 67-71. 9. Злобин В.К., Еремеев В.В., Васильев В.М. Стохастическая модель спутниковых изображений и ее использование для сегментации природных объектов // Там же. - С. 41-50. 10. Васюков В.Н., Голещихин Д.В. Восстановление полутоновых изображений на основе гиббсовского описания // Там же. - С. 58-66. 11. Соломатин И.И. Обзор методов предварительной обработки тоновых изображений для распознавания искусственных объектов // Изв. вузов. Приборостроение. - 1996. - Т. 39. - № 7. - С. 5-12. 12. Куринной Г.Ч. Математика: Справочник. - Харьков: Фолио; Ростов-н-Д.: Феникс, 1997. – 463 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=618 |
Версия для печати Выпуск в формате PDF (1.06Мб) |
| Статья опубликована в выпуске журнала № 4 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Знания в интеллектуальных системах
- Исследовательское проектирование в кораблестроении на основе гибридных экспертных систем
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
Назад, к списку статей



 , где
, где  ,
,  – соответственно число строк и столбцов изображения. Эталонный вектор изображения должен содержать только компоненты, относящиеся к контурным линиям (идеальная сегментация) и не содержать шумов (идеальная фильтрация).
– соответственно число строк и столбцов изображения. Эталонный вектор изображения должен содержать только компоненты, относящиеся к контурным линиям (идеальная сегментация) и не содержать шумов (идеальная фильтрация). , (1)
, (1) – нормированная на себя дисперсия исходного изображения с эталонным (равна единице);
– нормированная на себя дисперсия исходного изображения с эталонным (равна единице); – нормированная дисперсия изображения, полученного обработкой исходного по первому из оцениваемых методов;
– нормированная дисперсия изображения, полученного обработкой исходного по первому из оцениваемых методов;  – нормированная дисперсия изображения, обработанного последним (
– нормированная дисперсия изображения, обработанного последним ( -м) из оцениваемых методов;
-м) из оцениваемых методов;  – оператор транспонирования;
– оператор транспонирования;  – исходное изображение (до обработки) размерностью
– исходное изображение (до обработки) размерностью  ;
;  – эталонное изображение;
– эталонное изображение;  – изображение после обработки первым оцениваемым методом;
– изображение после обработки первым оцениваемым методом;  – изображение после обработки N-м методом. Эталонный вектор изображения
– изображение после обработки N-м методом. Эталонный вектор изображения  , (2)
, (2) – нормированное на себя расстояние между исходным и эталонным k-мерными векторами изображений (единица);
– нормированное на себя расстояние между исходным и эталонным k-мерными векторами изображений (единица);  – нормированное расстояние изображения, полученного обработкой исходного по перво- му из оцениваемых методов от эталонного;
– нормированное расстояние изображения, полученного обработкой исходного по перво- му из оцениваемых методов от эталонного;  – нормированное расстояние изображения, обработанного последним (N-м) методом от эталонного;
– нормированное расстояние изображения, обработанного последним (N-м) методом от эталонного;  – непрерывная функция исходного изображения;
– непрерывная функция исходного изображения;  – эталонного;
– эталонного;  ,
,  – соответственно непрерывные функции после преобразования
– соответственно непрерывные функции после преобразования  -м и
-м и  , (3)
, (3) – нормированное на себя евклидово расстояние между исходным и эталонным k-мерными векторами изображений (единица);
– нормированное на себя евклидово расстояние между исходным и эталонным k-мерными векторами изображений (единица); – нормированное евклидово расстояние изображения, полученного обработкой исходного по первому из оцениваемых алгоритмов от эталонного;
– нормированное евклидово расстояние изображения, полученного обработкой исходного по первому из оцениваемых алгоритмов от эталонного; – нормированное евклидово расстояние изображения, обработанного последним (N-м) методом от эталонного.
– нормированное евклидово расстояние изображения, обработанного последним (N-м) методом от эталонного. , (4)
, (4) где
где  – нормированный на себя синус угла между исходным и эталонным k-мерными векторами изображений (единица);
– нормированный на себя синус угла между исходным и эталонным k-мерными векторами изображений (единица); – нормированный синус угла между вектором изображения, полученным обработкой исходного по первому из оцениваемых методов и эталонным;
– нормированный синус угла между вектором изображения, полученным обработкой исходного по первому из оцениваемых методов и эталонным;  – нормированный синус угла между изображением, обработанным последним (N-м) методом и эталонным.
– нормированный синус угла между изображением, обработанным последним (N-м) методом и эталонным. , (5)
, (5) – обратная взаимная корреляция исходного с эталонным вектором;
– обратная взаимная корреляция исходного с эталонным вектором;  – обратная взаимная корреляция вектора на выходе первого алгоритма с эталонным;
– обратная взаимная корреляция вектора на выходе первого алгоритма с эталонным;  – обратная взаимная корреляция изображения, обработанного последним (N-м) методом с эталонным.
– обратная взаимная корреляция изображения, обработанного последним (N-м) методом с эталонным. .
. На рисунке 3 по оси аргументов 1 соответствует дисперсии, то есть выражению (1); 2 – расстоянию в пространстве непрерывных квадратичных функций (2); 3 – евклидову расстоянию (3); 4 – синусу угла между векторами (4); 5 – обратной взаимной корреляции векторов в соответствии с (5). Из рисунка 3 видно, что различные критерии оценки двух алгоритмов дают разные их величины.
На рисунке 3 по оси аргументов 1 соответствует дисперсии, то есть выражению (1); 2 – расстоянию в пространстве непрерывных квадратичных функций (2); 3 – евклидову расстоянию (3); 4 – синусу угла между векторами (4); 5 – обратной взаимной корреляции векторов в соответствии с (5). Из рисунка 3 видно, что различные критерии оценки двух алгоритмов дают разные их величины.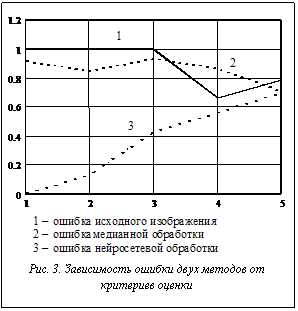 5. Воскобойников Ю.Е., Колкер А.Б. Адаптивный алгоритм фильтрации и преобразование изображений в векторный формат // Там же. - № 4. - С. 3-11.
5. Воскобойников Ю.Е., Колкер А.Б. Адаптивный алгоритм фильтрации и преобразование изображений в векторный формат // Там же. - № 4. - С. 3-11.