Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм идентификации сложных динамических объектов
Аннотация:
Abstract:
| Авторы: Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук, Круглов В.В. (byg@yandex.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14773 |
Версия для печати Выпуск в формате PDF (1.32Мб) |
Управление динамическими объектами является широко распространенной задачей в самых различных областях науки и техники. Одной из перспективных концепций построения систем управления является так называемое интеллектуальное управление. Системы, построенные с использованием данной концепции, обладают способностями, в какой-то степени аналогичными способностям человека к пониманию методов управления и обучению им [1]. В составе практически любой интеллектуальной системы управления используется модуль эмуляции (идентификации) объекта. Качество управления всей системы во многом зависит от этого модуля, что определяет актуальность рассматриваемой задачи. Анализ систем управления с модулем эмуляции позволяет сформулировать следующие требования к алгоритму работы эмулятора: - возможность эмуляции как линейных, так и сложных нелинейных объектов; - отсутствие ограничений на порядок моделей; - работоспособность при отсутствии априорной информации об объекте управления; - возможность использовать в модели априорную информацию, заданную в удобной для человека форме; - работоспособность при наличии шумов и помех; - последовательная обработка информации, возможность работы в реальном масштабе времени; - простота алгоритма вычислений; - экстраполирующие и интерполирующие свойства получаемых моделей должны быть соизмеримы со свойствами известных методов. Рассмотрим алгоритм эмуляции динамических объектов на основе самоорганизующейся системы нечеткого логического вывода – нечеткий дополняющий алгоритм [2,3], удовлетворяющий, как представляется, всем перечисленным требованиям. Допустим, что объект имеет скалярные вход Предположим, что регистрация входного и выходного сигнала объекта происходит в дискретные эквидистантные моменты времени ti, интервал между которыми значительно меньше постоянных времени объекта. Допустим далее, что на объекте может быть реализован эксперимент, заключающийся в регистрации N пар значений < Вход и выход исследуемого объекта связаны некой причинно-следственной связью, которую для стационарного объекта можно отразить нелинейным разностным уравнением m-го порядка:
С другой стороны, такую модель можно интерпретировать как модель многофакторного статического объекта с числом входов
где компоненты Допустим также, что о зависимости (2) имеется априорная информация, записанная в виде совокупности p продукционных нечетких правил вида: Пr: если х1 есть Аr1 и х2 есть Аr2 и … и хn есть Аrn, то у = уr, где r =1, 2,…, p – номер правила в базе знаний; xj (j=1,2,…,n) – компоненты вектора
Отметим, что данная априорная информация может и отсутствовать, то есть p = 0. Предлагаемый алгоритм идентификации состоит в реализации последовательности следующих шагов. Шаг 0. Задается e – погрешность аппроксимации. Устанавливается номер текущей обучающей точки i=1. Шаг 1. Выбирается очередная точка
где Шаг 2. Проверяется неравенство:
При невыполнении неравенства (5) – переход к шагу 3, иначе переход к шагу 5. Шаг 3. База знаний пополняется правилом вида: Пp+1: если х1 есть Аi1 и х2 есть Аi2 и … хn есть Аin, то уp+1= Значение p модифицируется: p:=p+1. Если точка Шаг 4. Параметры функций принадлежности
При такой коррекции значение параметров Шаг 5. Проверяется правило останова – просмотрены ли все N обучающих точек. Если правило останова не выполняется, то i=i+1 и переход к шагу 1, в противном случае – останов, база знаний считается сформированной. Рассмотренный алгоритм будем называть далее базовым нечетким дополняющим алгоритмом. Можно предложить большое число модификаций рассмотренного алгоритма, отличающихся видом нечетких продукционных правил, алгоритмом нечеткого логического вывода, условием добавления новых правил в базу знаний и т.п. Результаты вычислительного эксперимента Рассмотрим пример моделирования дискретного динамического объекта. Пусть имеется объект, имеющий один вход Объект имитируется существенно нелинейным разностным уравнением
при этом входной сигнал объекта представляет собой дискретный шум Эмуляция объекта производилась с помощью следующих моделей: 1) многослойного персептрона, содержащего три слоя нейронов: 1-й слой – 10 нейронов, 2-й – 5 нейронов, 3-й – 1 нейрон с сигмоидальными функциями активации [4]; 2) сигма-пи (
и настраиваемой по методу наименьших квадра- тов [4]; 3) разработанного базового нечеткого дополняющего алгоритма. В таблице приведены значения средней абсолютной погрешности моделей еср, полученных разными методами при тестировании реализацией входного сигнала, отличной от обучающей. Таблица
Из данных таблицы видно, что ошибки аппроксимации всех трех используемых моделей приблизительно соизмеримы, однако нечеткий дополняющий алгоритм выгодно отличается от многослойного персептрона тем, что в нем не возникает проблемы выбора структуры нейронной сети, а от сигма-пи нейронной сети тем, что позволяет аппроксимировать зависимость Необходимо отметить, что полученные с помощью предложенного алгоритма модели для гладких зависимостей Выбор порядка модели Остановимся на вопросе о выборе порядка модели m. В работе [6] рекомендуется последовательно увеличивать порядок модели до получения минимального значения оценки средней погрешности. В то же время, численное моделирование показывает, что зависимость средней погрешности em(m) от порядка модели m представляет собой унимодальную функцию дискретного аргумента (возрастание средней погрешности при превышении порядком модели порядка объекта объясняется недостатком информации для обучения модели).
Воспользовавшись тем, что зависимость em(m) унимодальна, а также тем, что максимальное значение порядка модели m обычно выбирается не больше 5-7, можно рекомендовать для поиска оптимального значения m дискретный вариант метода дихото- мии [7]. Список литературы 1. Нейроуправление и его приложения. - Кн.2. - Сигеру Омату, Марзуки Халид, Рубия Юсоф / Под ред. А.И. Галушкина, В.А. Птичкина. - М.: ИПРЖР, 2000. 2. Усков А.А. Адаптивная гибридная нейронная сеть. - М.: Деп. в ВИНИТИ РАН, 2002. - N396-В2002. 3. Усков А.А., Фомченков В.П., Окунев Б.В. Dinam_analysis. Свидетельство о регистрации программы для ЭВМ в Роспатенте N2002610429 от 25.03.2002. 4. Круглов В.В. Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. - М.: Физматлит, 2001. 5. Катковник В.Я. Непараметрическая идентификация и сглаживание данных. - M.: Наука, 1985. 6. Гаврилов А.И. Нейросетевая реализация процедуры идентификации динамических систем // Автоматизация и современные технологии. - 2002. № 3. - С.22-25. 7. Аоки М. Введение в методы оптимизации. - М.: Наука, 1977. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=669 |
Версия для печати Выпуск в формате PDF (1.32Мб) |
| Статья опубликована в выпуске журнала № 4 за 2002 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Оптимизация обработки информационных запросов в СУБД
- Сравнение сложных программных систем по критерию функциональной полноты
- Средства обеспечения надежности функционирования информационных систем
Назад, к списку статей



 и выход
и выход  (рис. 1), предлагаемый подход несложно расширить и на многомерные динамические объекты.
(рис. 1), предлагаемый подход несложно расширить и на многомерные динамические объекты. ,
,  >, при этом
>, при этом  . (1)
. (1) , при этом, заменяя в (1) переменные, приходим к соотношению:
, при этом, заменяя в (1) переменные, приходим к соотношению: , (2)
, (2) (j=1, 2, ... n) входного вектора
(j=1, 2, ... n) входного вектора  соответствуют значениям вектора
соответствуют значениям вектора  ,
,  , а
, а  – выходу объекта (верхние индексы i=1, 2, …, N указывают на порядковый номер опыта). При этом известны N пар значений (примеров) <
– выходу объекта (верхние индексы i=1, 2, …, N указывают на порядковый номер опыта). При этом известны N пар значений (примеров) < > (если i=1, то значения
> (если i=1, то значения  отражают предысторию входного сигнала, а
отражают предысторию входного сигнала, а  – начальные условия).
– начальные условия). (3)
(3) где
где  – центры нечетких чисел Arj;
– центры нечетких чисел Arj;  – постоянные параметры; yr – обычные (четкие) числа.
– постоянные параметры; yr – обычные (четкие) числа. . Если формируемая база знаний пуста, переход к шагу 3, иначе с помощью алгоритма нечеткого вывода Сугэно (Sugeno) 0-го порядка и с использованием имеющихся продукционных правил рассчитывается прогнозируемое значение
. Если формируемая база знаний пуста, переход к шагу 3, иначе с помощью алгоритма нечеткого вывода Сугэно (Sugeno) 0-го порядка и с использованием имеющихся продукционных правил рассчитывается прогнозируемое значение  [4]:
[4]: , (4)
, (4) – степень истинности предпосылки r-го правила.
– степень истинности предпосылки r-го правила. . (5)
. (5) , где Ai1, Ai2,…,Ain – нечеткие числа с треугольными функциями принадлежности (3) при значениях ai1=x1i, ai2=x2i, ... ain=xni соответственно (фактически добавление нового продукционного правила сводится к добавлению в базу знаний строки вида ).
, где Ai1, Ai2,…,Ain – нечеткие числа с треугольными функциями принадлежности (3) при значениях ai1=x1i, ai2=x2i, ... ain=xni соответственно (фактически добавление нового продукционного правила сводится к добавлению в базу знаний строки вида ). всех правил корректируются в соответствии с формулой:
всех правил корректируются в соответствии с формулой: (6)
(6) и один выход
и один выход  . Состояние входа и выхода объекта изменяется в дискретные моменты времени i = 0, 1, 2, …
. Состояние входа и выхода объекта изменяется в дискретные моменты времени i = 0, 1, 2, … (7)
(7) . Для идентификации использовалась выборка из 200 примеров.
. Для идентификации использовалась выборка из 200 примеров. ) нейронной сети, реализующей квадратичную функцию
) нейронной сети, реализующей квадратичную функцию
 произвольного (нелинейного) вида.
произвольного (нелинейного) вида.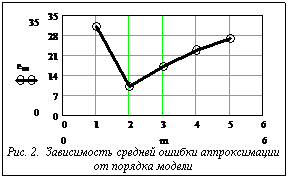 В качестве иллюстрации на рисунке 2 приведена данная зависимость для рассмотренного выше примера.
В качестве иллюстрации на рисунке 2 приведена данная зависимость для рассмотренного выше примера.