Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Онтологии и их применение
Аннотация:
Abstract:
| Автор: Девятков В.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15542 |
Версия для печати Выпуск в формате PDF (1.53Мб) |
Настоящая статья, с одной стороны, написана с целью дать читателям представление о новом направлении искусственного интеллекта, называемым онтологией, с другой стороны, рассказать о реализации и использовании конкретной онтологии. Содержание статьи представляет не столько обзор этого направления, сколько введение в те цели и задачи, в связи с которыми оно было сформировано. Что означает термин «онтология»? Люди, организации и программные системы вынуждены общаться друг с другом. Однако способ выражения знаний об одних и тех же вещах и на одном и том же языке может быть столь различным, что приводит к непониманию друг друга [1]. Это создает трудности обмена информацией между людьми, организациями и программами и, в частности, трудности формирования однозначно понимаемых требований и спецификаций для сложных систем. Несмотря на достаточно продвинутый уровень развития систем моделирования сложных систем, возможности взаимодействия созданных с их помощью программных моделей, вторичное использование и распространение этих моделей весьма ограничено. Это приводит к созданию программных моделей, мало отличающихся от уже существующих. Такая ситуация напоминает повторное изобретение велосипеда. Избежать этого можно устранением или сведением к минимуму концептуальной и терминологической путаницы и установлением однозначного понимания языка, используемого для формирования требований и спецификаций сложных систем. Такой язык должен прежде всего служить средством: коммуникации между людьми, имеющими различный взгляд на одни и те же вещи; взаимодействия между программными системами путем трансляции в него и из него; инструментальной поддержки для повторного использования благодаря формальной спецификации, унификации представления различных моделей, автоматизации проверки корректности, переводимости различных методов моделирования в унифицированное представление. Онтологией как раз называются представленные на некотором языке, обладающем перечисленными выше свойствами, знания о некоторой области интересов (среде, мире). Онтологии непременно сопутствует некая концепция этой области интересов. Чаще всего эта концепция выражается посредством определения базовых объектов (индивидуумов, атрибутов, процессов) и отношений между ними. Определение этих объектов и отношений между ними обычно называется концептуализацией. Концептуализация может быть неявной, то есть существующей только в чьей-то голове. Однако мы будем полагать, что онтология является явным представлением некоторой концептуализации и может иметь несколько форм представления: · неформальную на каком-либо естественном языке; · полуформальную на каком-либо структурированном подмножестве естественного языка; · слабоформализованную на каком-либо языке из области искусственного интеллекта с формальным синтаксисом; · формализованную на языке из области искусственного интеллекта с формальным синтаксисом, семантикой, значимым и полным механизмом вывода. Следующее определение онтологии, частично перекликающееся с приведенным в [2], суммирует различные определения онтологий: онтологией является общепринятая и общедоступная концептуализация определенной области знаний (мира, среды), содержащая базис для моделирования этой области знаний, определяющая протоколы для взаимодействия между агентами, использующими знания из этой области, и, наконец, включающая соглашения о представлении теоретических основ данной области знаний. Перспективы, связываемые с онтологиями, можно поделить на следующие категории: улучшение взаимодействия; унификация обмена данными; формализация процессов спецификации, улучшения надежности и обеспечения многократности использования систем моделирования. Улучшение взаимодействия связывают с уже упомянутыми надеждами на уменьшение терминологической и концептуальной путаницы и неоднозначности понимания на основе осуществления следующих мероприятий. · Создание в конкретной области человеческой деятельности унифицирующего нормативного ядра понятий, которое позволило бы достичь однозначного семантического толкования основных объектов и процессов этой области. Предполагается, что это нормативное ядро является семантической основой для порождения моделей в данной области, допускает нормативное переопределение и интерпретацию понятий ранее созданных моделей. · Создание однозначно понимаемой сети отношений между понятиями нормативного ядра, допускающей исследование на этой сети динамических и статических аспектов моделируемых систем, влияния на нее различных факторов, вывод и планирование ситуаций. · Обеспечение совместимости онтологий, разработанных различными коллективами, за счет широкого использования полисинонимии и ретранслируемости. · Обеспечение возможности коллективной работы по согласованию и унификации онтологий и их нормативного ядра. Унификацию обмена данными связывают с созданием интегрированных инструментальных программных средств, построенных на основе использования упомянутых выше нормативного ядра и сети отношений. Эти средства должны обеспечить возможность обмена данными для созданных или создаваемых систем моделирования и выступают как средство межъязыкового общения, как своеобразный декларативный язык, на который переводятся другие языки и из которого перевод осуществляется в индивидуальный язык пользователя. Эти средства должны иметь в своем составе поддерживаемые, развивающиеся и доступные для использования извне интегрированные модели. Формализацию процессов спецификации, повышения надежности и обеспечения многократности использования систем моделирования связывают с ролью онтологий, которую они призваны играть для развития систем моделирования. · Язык онтологии выступает в этом случае как средство спецификации систем моделирования и является декларативным. Роль онтологии зависит от степени выразительности, формализованности и других свойств декларативного языка онтологии. · Повышение надежности систем моделирования связывают с возможностью и удобством полуформального и формального анализа декларативного описания на языке онтологии. При этом, говоря о формальном анализе, имеют в виду, что описание допускает формальный вывод (доказательство) наличия тех или иных свойств описания. · Обеспечение многократности использования предполагает наличие в онтологии метауровня, позволяющего настроить онтологию на конкретную задачу применения, определить степень ее пригодности для задачи и при необходимости модифицировать или расширить. Этапы создания онтологии. Общепринятой или тем более стандартизованной процедуры создания онтологии не существует. Рекомендации носят общий характер, во многом схожий с рекомендациями для создания программных моделей сложных систем. · Определение цели и постановка задачи. На этом этапе особенно важно понять зачем нужна онтология, как и кем она будет использоваться. · Построение. Этот этап разбивается на три подэтапа: формализация понятий, кодирование и интеграция. В процессе формализации понятий осуществляется выявление основных объектов и отношений предметной области, текстовое описание этих объектов и отношений, сопоставление этим объектам и отношениям термов. В процессе кодирования формируется описание в каком-либо формальном языке результатов предыдущего подэтапа. Обычно кодирование включает описание с использованием введенных термов необходимых метаутверждений, выбор формального языка для кодирования, кодирование в выбранном языке. Подэтап интеграции выполняется параллельно двум упомянутым и требует тщательного обдумывания того, каким образом вновь создаваемая онтология будет интегрироваться с уже существующими. · Оценка. На этом этапе осуществляется обдумывание и формирование вопросов, на которые онтология должна давать ответы, выбирается программная среда для реализации онтологии. · Документирование. В данном случае понимается тщательное описание всех дополнительных термов и утверждений, необходимых для реализации онтологии. Теоретический базис и программные средства для реализации онтологий. Теоретический базис, положенный в основу создания конкретной онтологии, достаточно типичен. Принципиальным же для создания онтологий является не процедурный, а декларативный подход. Теоретической основой большинства языков, используемых для кодирования онтологий, являются различные исчисления, в основе которых, как правило, лежит логика предикатов первого порядка с равенством. Обсуждаются и другие логики как теоретическая основа для онтологий. В качестве программных средств для реализации онтологии, точнее исчислений, стоящих за онтологиями, используются языки Пролог или Лисп. Энергетическая эффективность теплоснабжения. В последнее время в отечественных и зарубежных источниках уделяется много внимания вопросам энергетической эффективности жилых зданий. Утверждается [3], что в настоящее время от 40 до 50% энергии, потребляемой в развитых странах, расходуется на обогрев зданий и этот расход имеет тенденции к росту. В работе [4] авторы оценивают долю потребления энергии на нужды отопления жилых зданий в Западной Европе в 52% от всей производимой энергии. Близкая оценка в 40% называется в США. Многие другие источники называют похожие цифры для Канады, России, Южной Африки. Некоторые исследователи сделали попытку оценить эффективность исследований в области экономии энергии. Авторы работы [5] подсчитали, что только за счет проектирования более эффективных систем теплоснабжения зданий можно высвободить до 30% энергии. Департамент энергии Англии полагает, что улучшенное проектирование систем теплоснабжения жилых зданий может уменьшить потребление энергии на 50% [6]. Самые оптимистические оценки, включающие использование энергии ветра, солнца и термальных источников для систем теплоснабжения, прогнозируют возможный процент экономии энергии до 70%. Все это свидетельствует о том, что необходимы средства эффективного проектирования систем теплоснабжения, позволяющие осуществить экономию энергии. Отправным материалом для проектирования реальных систем теплоснабжения здания является архитектурный проект, который определяет размеры здания и его помещений, конструкции всех элементов здания, расположение и размеры окон и дверей, расположение инженерных сооружений, в частности систем теплоснабжения, канализации, вентиляции и т.п., то есть всего, что необходимо в соответствии с действующими строительными нормами и правилами. Для того чтобы иметь возможность осуществлять оптимальное автоматизированное проектирование систем теплоснабжения жилых зданий, необходимо иметь формальную модель, с помощью которой можно было бы решать задачу. Какие же соображения должны быть положены в основу подобной модели? С одной стороны, известны различные математические модели, которые используются при проектировании систем теплоснабжения зданий, основанные на законах теплопередачи (например, дифференциальные уравнения, линейные уравнения стационарного режима). Все было бы хорошо, если бы задача выглядела как классическое совместное решение системы уравнений для нахождения оптимальных параметров системы теплоснабжения по известным исходным данным. К сожалению, для большинства реальных задач, использование классического подхода встречает непреодолимые препятствия, связанные с тем, что: 1) при оптимизации в рассмотрение должны быть включены показатели затрат, выраженные в виде эмпирических формул, для расчета, например, стоимости жизненного цикла здания и других параметров, множества разнородных условий и требований, диктуемых действующими нормами и правилами; 2) при классическом подходе невозможно учесть требования, которые носят субъективный характер и изменяются по мере продвижения процесса проектирования; 3) упомянутый классический подход не охватывает метауровня, без которого современная автоматизация проектирования неосуществима, а именно уровня планирования алгоритмов оптимального поиска в пространстве допустимых значений. Исходя из этого, авторы остановились на современном логическом подходе к решению задачи оптимального автоматизированного проектирования систем теплоснабжения жилых зданий, в основу которого положена комплексная онтология теплоснабжения, включающая в себя достоинства известных моделей и позволяющая преодолеть перечисленные препятствия. После того как онтология сформирована, ставятся так называемые формальные компетентные вопросы, на которые предполагается получать ответ с помощью онтологии. Эти вопросы формулируются как теоремы, в результате логического доказательства которых и получается ответ на них. В настоящей статье выделяется два типа компетентных вопросов: а) прямые вопросы (анализа) - "каковы будут эксплуатационные характеристики здания (комфортность и стоимость) при заданных значениях параметров здания и системы теплоснабжения (конструкции, применяемые материалы, цены)?"; б) обратные вопросы (синтеза) - "каковы должны быть параметры конструкции чтобы обеспечить требуемые или наилучшие (оптимальные) эксплуатационные характеристики здания при заданных условиях, определяемых константными параметрами (климатическими, стоимостными и т.п.)?". Комплексная онтология теплоснабжения. Онтология теплоснабжения зданий основана на аксиоматическом представлении знаний из этой предметной области. Аксиомы подразделяются на четыре группы: идентификации, вычислений, планирования и оптимизации. Мы рассмотрим первые три группы аксиом. Назначением идентификационных аксиом является описание всех типов переменных и отношений, в которые эти переменные вступают друг с другом. Будем полагать, что здание в целом, включая систему теплоснабжения, имеет множество объектных параметров X={x1, ..., xN}, включая все известные и неизвестные, постоянные и переменные, исходные и промежуточные, оценочные и конструктивные и т.п. В реальном проектировании требуется находить или уточнять значения части этих параметров, каждый из которых, как правило, должен попадать в определенный интервал значений. Интервалом значений также задаются известные параметры и ограничения в задачах оптимизации. Поэтому значением каждого параметра xÎX в нашей онтологии является интервал – множество действительных чисел r, таких что l£r£h, где l, h – границы интервала. Интервал значений параметра x будем обозначать [x] = [l, h]. Каждый параметр в нашей онтологии представляется предикатом параметр (x, [l, h]), истинным, когда переменная x существует и лежит в интервале [l, h], где l, h являются соответственно левой и правой границами интервала. В дальнейшем все переменные будем обозначать малыми буквами, а константы большими. Введем множество отношений R = {r1, ..., rI}. Каждое отношение ri связывает некоторое множество параметров Yi и используется для вычисления неизвестных значений параметров Yiвых Í Yi по известным значениям параметров Yiвх Í Yi. Этот процесс называется вычислением отношения ri. Как осуществляется вычисление неизвестных значений в зависимости от множества известных определяют аксиомы вычислений. В самом общем случае предполагается, что для вычисления любого неизвестного параметра y ÎYi всегда найдется набор переменных Yiвх , значения которых известны и позволяют вычислить y. Отношения являются теми кирпичиками, из которых формируются более сложные отношения в конкретной онтологии теплоснабжения (или в общем случае в любой другой онтологии). Для этого в каждом экземпляре используемого отношения ri вместо его переменных Yi подставляются параметры подмножества Xm Í X, а сам экземпляр получает уникальный порядковый номер m. Каждый такой экземпляр отношения ri представляется предикатом экземпляр (ri, m, Xm). Множество параметров Xm одного экземпляра отношения ri может совпадать, пересекаться или не пересекаться с множествами параметров других экземпляров, то есть вычисляемые (выходные) параметры одного экземпляра могут быть входными для других, в результате чего получается некая сеть экземпляров, которую можно изобразить в виде графа, если каждый экземпляр представить его вершиной, а параметры ребрами. Таким образом, все знания о проектируемой системе теплоснабжения, будь то система уравнений или какие-либо эмпирические формулы, представляются в виде множества предикатов типа параметр и экземпляр. Эти простейшие предикаты и составляют группу аксиом идентификации. Следующий этап формирования онтологии - формулировка аксиом вычислений, задающих правила вычисления отношений. Как уже отмечалось, каждое отношение ri = ri(Yi) связывает некоторое множество своих параметров Yi и используется для вычисления неизвестных значений параметров Yiвых Í Yi , связанных отношением ri по известным значениям параметров Yiвх Í Yi. Разбиений Yi на Yiвх и Yiвых может быть достаточно много (K), каждому из них соответствует свой оператор fik(Yiвх , Yiвых), по которому и осуществляется вычисление. Совокупность всех таких операторов для данного отношения ri составляет множество F(ri) = {fi1,…, fiK}. Поскольку интервальная арифметика лежит в основе вычисления формул, то, прежде чем переходить к формулировке аксиом вычисления отношений, напомним элементарные правила вычислений в этой арифметике [7]. Операции сложения, вычитания, умножения и деления над двумя интервалами A и B определяются следующим образом: [l1, h1] + [l2, h2], = [l1 + h1, l2 + h2], [l1, h1] - [l2, h2]A - B = [l1 - h2, l2 - h1], [l1, h1] * [l2, h2]= [min{l1×h1, l1×h2, l2×h1, l2×h2}, max{l1×h1, l1×h2, l2×h1, l2×h2}], [l1, h1] / [l2, h2]= [min{l1/h1, l1/h2, l2/h1, l2/h2}, max{l1/h1, l1/h2, l2/h1, l2/h2}], 0Ï[l2, h2]. Покажем теперь, как формулируются аксиомы для вычисления отношений ri(Yi) сначала в общем виде. Пусть Yi = {yi1 ,…, yiq}. Введем предикат оператор (fik (Yikвх, Yikвых)), который истинен, если известными значениями параметров оператора fik является множество Yikвх Í Yi и в результате вычисляются значения неизвестных параметров Yikвых Í Yi. Тогда аксиома вычислений отно- шения ri в общем виде выглядит следующим образом: Ù параметр (yi1, [l1, h1])Ù…Ù параметр (yiq, [lq, hq])Ù (оператор ( fi1 (Yi1вх, Yi1вых )) Ú…Ú оператор (fiK (YiKвх, YiKвых ))) É отношение (ri, Yi ). В конкретных отношениях обобщенный предикат оператор заменяется на выражения для вычисления выходных переменных по входным. Рассмотрим теперь пример аксиомы вычислений для отношения сложения, связывающего три параметра y1, y2, y3 отношением сложения r+. Для отношения сложения возможны только три оператора: а) вычисляющий по известным y1 и y2, неизвестную y3, б) вычисляющий по известным y1 и y3, неизвестную y2 и в) вычисляющий по известным y3 и y2, неизвестную y1. Аксиома вычислений для отношения r+ будет выглядеть следующим образом: (параметр (y1, [l1, h1]) Ù параметр (y2, [l2, h2]) Ù параметр (y3, [l3, h3]) Ù ([l3, h3] = [l1, h1] + [l2, h2] Ú [l2, h2] = [l3, h3] - [l1, h1] Ú [l1, h1] = [l3, h3] - [l2, h2]) É отношение (r+, y1, y2, y3). Аксиомы вычислений должны быть заданы для всех отношений, участвующих в онтологии. После того как сформулированы аксиомы идентификации и вычислений, возникает задача планирования вычислений. Суть планирования вычислений (например, [8]) заключается в следующем. Перед началом вычислений задается множество начальных значений входных параметров в виде множества предикатов параметр (xn, [Ln, Hn]). Обозначим это множество параметров E0. Первый шаг планирования – это нахождение тех предикатов типа экземпляр (ri, m, Xm), отношения которых могут быть вычислены согласно аксиомам вычислений на множестве E0. Обозначим это множество экземпляров S0. После нахождения множества S0 осуществляется вычисление отношений экземпляров множества S0 и получается новое множество значений параметров E1, и все повторяется сначала, но вместо множества E0 используется множество E1. Процесс получения множеств значений параметров E0, E1,… и соответствующих им множеств экземпляров S0, S1,… может продолжаться бесконечно. На практике останов может происходить в результате: появления на некотором этапе вычислений пустого множества Sr, что соответствует отсутствию вычислимых отношений; предписанного заранее числа допустимых итераций; достижения устраивающего пользователя результата; каких-либо других критериев останова. Поскольку в основе вычислений лежит интервальная арифметика, то можно воспользоваться ее результатами, позволяющими при определенных условиях осуществить сходимость итеративной процедуры вычисления интервальных значений параметров к некоторым локализующим интервалам, содержащим требуемые решения [7]. В любом случае, для того чтобы описанная итеративная процедура вычислений могла быть осуществлена, необходимо ввести аксиомы планирования, задающие правила этого итеративного вычисления. Введем предикат проверка (Xm, Ej, m) истинный, если экземпляр m какого-либо отношения вычислим на множестве известных параметров Ej, то есть имеется экземпляр отношения ri с номером m (истинен предикат экземпляр (ri, m, Xm)) и истинен предикат отношение (ri, Xm). Тогда аксиома проверки на включение экземпляра с номером m в множество Sj задается аксиомой экземпляр (ri, m, Xm) Ù Xm Î Ej Ù отношение (ri, Xi) É проверка (Xm, Ej, m), а аксиома итеративного дополнения множеств Sj и Ej по результатам поверки будет следующей: проверка (Xm, Ej, m) Ù состояние (Ej, Sj) Ù m £ M É состояние (Ej È Xm, Sj È m), где M – максимальное число экземпляров, используемых в конкретной онтологии, а предикат состоя- ние (Ej, Sj) определяет текущий состав множеств Ej, Sj. Аксиомы идентификации, вычисления и планирования позволяют давать ответы на прямые вопросы. Для того чтобы давать ответы на обратные вопросы, необходимы аксиомы, называемые оптимизационными. Оптимизация. Мы изложили принципы формирования и использования онтологии теплоснабжения для ответа на прямые вопросы. Чтобы отвечать на обратные вопросы, необходимо иметь возможность нахождения оптимальных значений параметров по критериям эффективности. Это означает, что в онтологии должна быть группа соответствующих аксиом оптимизации. Критериями эффективности будем считать комфортность и стоимость здания, причем для достижения энергетической эффективности стоимость должна включать все затраты жизненного цикла здания, то есть расходы на эксплуатацию, энергию, ремонт. Это означает, что задача оптимизации является многокритериальной, а критерии противоречивы. В теории математического программирования такая задача ставится как векторная задача оптимизации с ограничениями [8, 9]. Первая постановка приводит задачу к однокритериальной. Задачи б) и в) многокритериальные, из которых наиболее общая последняя. Рассмотрим подход к ее решению. Существующие методы решения многокритериальных задач связаны с тем или иным учетом системы предпочтений человека и на основе этого с выбором какого-либо принципа оптимальности. Методы делятся на несколько групп: методы назначения весовых коэффициентов для каждого критерия, упорядочения критериев по важности, оптимизации наихудшего критерия, минимизации суммы отклонений критериев от идеальных значений и интерактивной оптимизации. Не во всех методах легко выразить предпочтения разработчика системы и не все методы дают в конечном итоге оптимальное по Парето решение. Из этих соображений авторы привлекли методы оптимизации наихудшего критерия (максимизация минимальной компоненты) [9], сущность которых состоит в следующем. Решается задача оптимального поиска по каждому критерию отдельно и определяются наилучшие vmax и наихудшие vmin значения всех критериев v(x). Далее для каждого критерия вычисляются относительные критерии по формуле u(x) = (v(x) - vmin) / (vmax - vmin). Среди относительных критериев существует минимальный для любого решения. Оптимальным считается решение x*, имеющее максимальное значение минимального относительного критерия среди допустимых решений.
Для введения аксиомы оптимизации введем сначала ряд предикатов. Конкретное значение вектора переменных x (точку в пространстве переменных) будем обозначать Xi. Множество точек, составляющих комплекс, обозначим Cx = { X1,…, Xp}. Предикат максимум (Cx, Xmax, V) будет истинным в том случае, если точка Xmax имеет наибольшее значение критерия V среди точек комплекса Cx. Предикат центр (Cx, Xc) истинный, если точка Xc - центр тяжести множества точек Cx. В предикате симметрия (Xr, Xmax, Xc) точка Xr симметрична точке Xmax относительно центра симметрии Xc. Предикат оптимум (Cx, Opt, e, V) означает, что комплекс Opt есть аппроксимация оптимума критерия V и точки комплекса отстоят друг от друга не более чем на e при начальном комплексе Cx. Наконец, предикат расстояние (Cx, e) истинный, когда расстояние между точками комплекса Cx меньше e. Теперь мы можем записать аксиому, согласно которой находится оптимальное решение по критерию V методом, описанным выше: (расстояние (Cx, e) Ù Cx = Opt,) Ú [максимум (Cx, Xmax, V) Ù Cx- = Cx - Xmax Ù центр (Cx-, Xc) Ù симметрия (Xr , Xmax, Xc) Ù Cx+ = { Cx-, Xr} Ù оптимум (Cx+, Opt, e, V)] É оптимум (Cx, Opt, e, V). В этой рекурсивной аксиоме каждый вызов улучшает аппроксимацию Cx, заменяя ее на Cx+, за счет удаления из комплекса точки Xmax с наихудшим значением критерия V и добавления новой точки Xr до тех пор, пока комплекс не сойдется в шар диаметра e. Таковы основные черты комплексной онтологии теплоснабжения, предназначенной для решения задач анализа и оптимизации при автоматизированном проектировании индивидуальных зданий. Конечно, это не онтология целиком, все предикаты, которые мы ввели, кроме аксиом идентификации, требуют своих правил, выражающих их через более простые предикаты. Однако были описаны подходы к построению логической модели, ее структура, все применяемые методы. На основе изложенной онтологии была написана логическая программа на языке SWI-Prolog [11], переносимая без изменений в любую среду Пролога, поддерживающую Эдинбургский стандарт. Программа предназначена для расчета системы теплоснабжения и эксплуатационных свойств зданий, которые представлены базой данных, состоящей из идентификационных аксиом. Программа независима от базы данных и может использоваться для разных зданий. В качестве практического примера был взят готовый типовой проект жилого индивидуального двухэтажного дома [12], предназначенного для строительства в центральных районах Европейской части России в III строительно-климатическом районе по СНиП 2.04.05-86. Была поставлена задача, во-первых, получить оптимальное решение, а во-вторых, сравнить его с решениями типового проекта и исследовать влияние различных факторов на параметры оптимального решения и найти главные. Для здания была разработана онтология, позволяющая рассчитывать температуры воздуха в зонах здания, температуры внутренних поверхностей стен, тепловую устойчивость конструкции здания, нагрузку системы отопления и размеры радиаторов, а также стоимость жизненного цикла здания и отдельных компонент: стоимость строительства, величину годовых отчислений на эксплуатацию, годовые затраты на топливо.
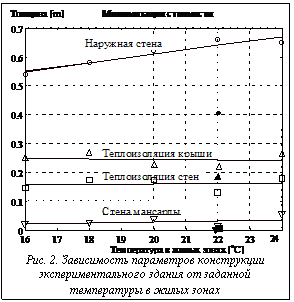
Была проведена серия экспериментов по минимизации стоимости жизненного цикла системы. На рисунке 1 изображена зависимость различных составляющих стоимости жизненного цикла от назначаемых температур в помещении. Все стоимости приведены к одному году эксплуатации. Для выявления зависимости диапазон изменения температур 16-24оС взят несколько шире, чем регламентируется СНиП. Естественно, чем выше эта температура, тем лучше теплозащитные свойства ограждения и выше комфортность здания. Видно, что все компоненты стоимости возрастают. Однако в большей степени (на 10%) возрастает стоимость топлива, в то время как стоимость конструкции увеличивается сравнительно мало, менее чем на 5%. На рисунке 2 показаны зависимости некоторых параметров, входящих в число переменных параметров. Они не проявляют какой-либо ярко выраженной тенденции при довольно большом разбросе, за исключением толщины наружной стены здания, которая устойчиво возрастает. По-видимому, это и есть параметр, который наиболее тесно связан с температурой в жилых зонах. Кроме того, на рисунках показаны параметры решения, соответствующие исходному проекту. При прочих равных условиях оптимизированное проектное решение, полученное с помощью рассмотренной в статье онтологии, сокращает стоимость жизненного цикла на 10% в основном за счет сокращения расхода топлива на 35%, повышая теплозащитные свойства здания. Однако следует учесть, что при расчете были применены цены на строительные материалы, характерные для сегодняшнего рынка. Результаты другой серии экспериментов, в которой вводились ограничения на стоимость жизненного цикла и исследовалось их влияние на параметры конструкции и другие критерии, показаны на рисунках 3 и 4. Рисунок 3 подтверждает совершенно очевидный результат - рост температуры с ростом затрат. Рисунок 4 позволяет проанализировать, как изменяется структура затрат с увеличением стоимости жизненного цикла: дополнительные затраты идут, в основном, на топливо при относительно постоянной стоимости конструкции. В заключение отметим, что в работе предложена методология экономии затрат энергии в проектируемых жилых зданиях на основе автоматизированного использования комплексной онтологии теплоснабжения, которая позволяет учесть весь набор факторов и параметров при проектировании, включая субъективные предпочтения разработчика и заказчика.
И, наконец, хотелось бы отметить, что так как вычисления осуществлялись приближенными методами, а выбор начальных значений для расчета производился достаточно произвольно, то, на наш взгляд, точность выявленных закономерностей требует дополнительной проверки. Список литературы 1. Налимов В.В. Вероятностная модель языка. - М.: Наука, 1979. 2. Rousseau P. G., Mathews E. H., Needs and trends in integrated building and HVAC thermal design tools. Building and Environment, 28(4), 439-452, 1993. 3. Clarke J. A. and Maver T. W., Advanced design tools for energy conscious building design: Development and dissemination. Building and Environment, 26, 25-34, 1991. 4. Bevington R., Rosenfeld A. H., Energy for buildings and homes. Scient. Amer., September, 39-45, 1990. 5. Mathews E. H., Richards P. G., An efficient tool for future building design. Building and Environment, 28(4), 409-417, 1993. 6. Ushold M., Gruninger M., "Ontologies: Principles, Methods and Application" Knowledge Engineering Reviw. Vol. 11, No 2, 1996. 7. Алефельд Г., Херцбергер Ю., Введение в интервальные вычисления. /Пер. с англ. -М.:Мир, 1987. 8. Иванищев В.В., Автоматизация моделирования потоковых систем. - Л.: Наука, 1986. 9. Машунин Ю. К., Методы и модели векторной оптимизации. - М.: Наука, 1986. 10. Box M. J., A new method of constrained optimisation and comparison with other methods. The Comp. Journal, 8, 42-52, 1965. 11. SWI-Prolog 2.7, Reference Manual, University of Amsterdam, 1996. 12. Типовой Проект 144-000-669.13.87 ТК-113-4-3 Одноэтажный одноквартирный 3-комнатный мансардный жилой дом. - Госстрой Лит. ССР, 1987. 13. Соснин Ю.П., Бухаркин Е.Н., Отопление и горячее водоснабжение индивидуального дома: Справ. пособие.- М.: Стройиздат, 1993. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=886 |
Версия для печати Выпуск в формате PDF (1.53Мб) |
| Статья опубликована в выпуске журнала № 3 за 2000 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Эвристические и точные методы программной конвейеризации циклов
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Знания в интеллектуальных системах
- Системы баз данных и знаний, разработанные в Республике Куба
- Спецификация объектно-ориентированной модели данных с помощью отношений
Назад, к списку статей




 Решение задачи требует нахождения оптимального решения в однокритериальном смысле. Среди методов оптимизации с ограничениями здесь применимы методы прямого поиска без вычисления градиентов, потому что онтология не содержит в явном виде аналитического выражения. Среди множества таких методов был выбран метод Бокса [10] как довольно простой и отвечающий всем предъявленным требованиям. Вначале критерий вычисляется в нескольких точках, случайным образом распределенных по допустимой области. Совокупность этих точек называется комплексом. Далее осуществляется итерационная процедура поиска оптимума (в невыпуклом случае - локального), которую мы опишем для случая минимизации. Среди p точек комплекса выбирается одна с максимальным значением функции и она отображается симметрично относительно центра тяжести остальных p-1 точки. Если полученная точка не является допустимой, то она сдвигается к центру тяжести остальных точек, пока не попадет в область допустимых значений. Эта точка замещает свой прообраз в комплексе. Такая процедура позволяет комплексу перемещаться в сторону убывания критерия и сжиматься вокруг оптимальной точки, улучшая ее аппроксимацию. Естественно, должен существовать какой-либо принцип завершения итераций по достижению заданной точности.
Решение задачи требует нахождения оптимального решения в однокритериальном смысле. Среди методов оптимизации с ограничениями здесь применимы методы прямого поиска без вычисления градиентов, потому что онтология не содержит в явном виде аналитического выражения. Среди множества таких методов был выбран метод Бокса [10] как довольно простой и отвечающий всем предъявленным требованиям. Вначале критерий вычисляется в нескольких точках, случайным образом распределенных по допустимой области. Совокупность этих точек называется комплексом. Далее осуществляется итерационная процедура поиска оптимума (в невыпуклом случае - локального), которую мы опишем для случая минимизации. Среди p точек комплекса выбирается одна с максимальным значением функции и она отображается симметрично относительно центра тяжести остальных p-1 точки. Если полученная точка не является допустимой, то она сдвигается к центру тяжести остальных точек, пока не попадет в область допустимых значений. Эта точка замещает свой прообраз в комплексе. Такая процедура позволяет комплексу перемещаться в сторону убывания критерия и сжиматься вокруг оптимальной точки, улучшая ее аппроксимацию. Естественно, должен существовать какой-либо принцип завершения итераций по достижению заданной точности.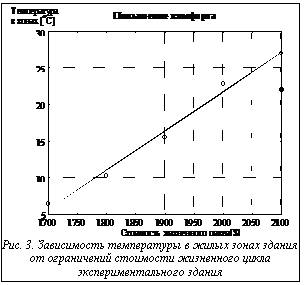 Из параметров проекта были выбраны двенадцать в качестве переменных - это толщины основных элементов ограждающей конструкции. Критериями, по которым проводилась оптимизация, в различных вариантах решения выступали температуры воздуха в жилых зонах, тепловая устойчивость, первоначальная стоимость здания и, конечно, стоимость жизненного цикла. Решение проводилось следующим образом. Константы дома были взяты из проекта, строительной справочной литературы [13] и действующих СНиП. В зависимости от варианта решения заполнялась база данных (отнесение переменных к той или иной группе также задается в базе данных). Потом искалось оптимальное решение согласно описанной онтологии.
Из параметров проекта были выбраны двенадцать в качестве переменных - это толщины основных элементов ограждающей конструкции. Критериями, по которым проводилась оптимизация, в различных вариантах решения выступали температуры воздуха в жилых зонах, тепловая устойчивость, первоначальная стоимость здания и, конечно, стоимость жизненного цикла. Решение проводилось следующим образом. Константы дома были взяты из проекта, строительной справочной литературы [13] и действующих СНиП. В зависимости от варианта решения заполнялась база данных (отнесение переменных к той или иной группе также задается в базе данных). Потом искалось оптимальное решение согласно описанной онтологии.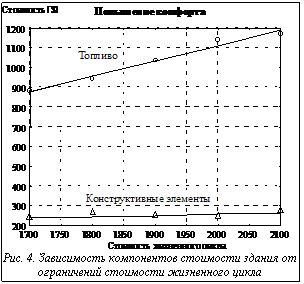 Программная реализация методологии и ее экспериментальное апробирование на типовом проекте позволяют сделать следующие выводы: а) применение методологии позволяет сократить расход топлива на 35%, что уменьшает расходы на жизненный цикл здания по сравнению с типовым проектом на 10%; б) на достижение подобного эффекта основное влияние оказывают параметры основных ограждающих конструкций; в) оптимальные конструктивные решения для разных соотношений комфортности и стоимости в диапазоне, отвечающем стандартам, довольно близки друг к другу, что позволяет для схожих по базовым конструктивным решениям зданий, отличающихся соотношением комфортности и стоимости, варьировать только параметрами системы теплоснабжения; г) полученные оптимальные конструктивные параметры превосходят типовое решение по теплозащитным свойствам наружных стен, что свидетельствует о недоучете эксплуатационных затрат при типовом проектировании.
Программная реализация методологии и ее экспериментальное апробирование на типовом проекте позволяют сделать следующие выводы: а) применение методологии позволяет сократить расход топлива на 35%, что уменьшает расходы на жизненный цикл здания по сравнению с типовым проектом на 10%; б) на достижение подобного эффекта основное влияние оказывают параметры основных ограждающих конструкций; в) оптимальные конструктивные решения для разных соотношений комфортности и стоимости в диапазоне, отвечающем стандартам, довольно близки друг к другу, что позволяет для схожих по базовым конструктивным решениям зданий, отличающихся соотношением комфортности и стоимости, варьировать только параметрами системы теплоснабжения; г) полученные оптимальные конструктивные параметры превосходят типовое решение по теплозащитным свойствам наружных стен, что свидетельствует о недоучете эксплуатационных затрат при типовом проектировании.