Программные продукты и системы

Каждый проект, в том числе и в сфере ПО, имеет свой жизненный цикл – последовательность фаз, задаваемую исходя из потребностей управления проектом. В любом проекте по разработке информационных систем может возникнуть неопределенное событие или условие, которое повлияет хотя бы на одну цель проекта, то есть существуют риски, которые могут и нарушить целостность проекта, нанеся ему вред, и принести пользу, улучшив его состояние [1]. В любом случае, чтобы разработка информационной системы продвигалась по плану, необходимо иметь четкое представление о рисках в проекте и уметь ими управлять. Процесс управления рисками тесно интегрирован с общим жизненным циклом проекта. Оценка рисков может быть начата на этапе выработки концепции.

Считается, что проект, в котором число рисков сведено к минимуму, наименее прибыльный, поскольку отсутствие рисков привлекает большое количество конкурентов, а значит, возможная прибыль уменьшается. Риски отличаются от проблем и трудностей, так как имеют отношение к будущим, потенциально возможным негативным результатам и убыткам. Риски могут стать проблемами, если ими управлять неэффективно. Цель управления рисками – максимизировать их положительное влияние (открывающиеся возможности), минимизируя при этом связанные с ними негативные факторы (убытки). Эффективный процесс выявления рисков и управления ими помогает достичь разумных компромиссов между упомянутыми опасностями и открывающимися возможностями [2].

Основными методологиями управления IT-рисками являются CORAS, OCTAVE и CRAMM. Однако они и им подобные имеют множество недостатков: нет подробных рекомендаций по проведению повторных оценок рисков, отсутствуют методы количественной оценки рисков и четкие инструкции по мониторингу их состояния. Используемые в настоящее время стандарты в области защиты информации рассматривают анализ и управление информационными рисками, однако не отражают ряд важнейших деталей, которые необходимо учитывать при разработке практических методик управления рисками.

В качестве методик управления рисками чаще всего коллективы разработчиков используют PMBoК и MSF, определяющие основные этапы жизненного цикла управления рисками: планирование управления рисками, идентификация, анализ рисков, планирование реагирования на риски, мониторинг, извлечение уроков [3].

С точки зрения методологии управления рисками важным и наиболее сложным этапом является анализ рисков. При этом, если методы качественного анализа широко известны и применяемы, то методы количественного анализа при всем разнообразии еще недостаточно распространены. Качественный анализ рисков применяется на начальных этапах управления рисками, методы качественного анализа сравнительно легко подстраиваются под параметры проекта и дают возможность получить грубую оценку совокупного риска проекта. Методы количественного анализа обычно требуют наличия информации о рисках, накопленной при помощи качественного анализа, и при корректной подстройке параметров дают более точные результаты. Среди методов количественного анализа можно отметить анализ чувствительности, анализ сценариев, метод достоверных эквивалентов, метод Монте-Карло, метод исторических симуляций, деревья событий, деревья отказов, логико-вероятностные методы, эвристические методы количественного анализа.

Качественная оценка рисков проводится с помощью оценки таких параметров риска, как его вероятность, угроза и ожидаемая величина [4].

При оценке риска наиболее часто используются экспертная оценка параметров риска и ее отображение в виде карты рисков. На одной из осей откладывается вероятность возникновения риска, на другой – угроза риска. Ожидаемая величина – итоговое воздействие риска, которое вычисляется по формуле Ожидаемая величина риска = Вероятность*Угроза.

В зависимости от полученного результата ячейка карты рисков окрашивается в определенный цвет (обычно используются зеленый, желтый и красный). Данный подход позволяет оценивать только каждый риск проекта по отдельности, но не совокупный риск. Для проведения такой оценки используются различные эвристические методы. Например, оценивается время, затрачиваемое на устранение всех рисков, находящихся в красной зоне. Если это время составляет более 20 % от общего времени проекта – статус проекта в красной зоне, если в пределах 10–20 % – в желтой, если менее 10 % – в зеленой зоне.

Для проведения количественного анализа рисков предлагается модель совокупного риска проекта, основанная на методе Монте-Карло.

Ставится задача нахождения некоторой оценки времени продолжительности работы над проектом (с учетом всех его рисков), то есть необходимо оценить влияние всех рисков проекта на его длительность во времени.

Пусть n – количество рисков проекта на данный момент. Предполагается, что риски никак не взаимодействуют между собой, то есть исключена ситуация, когда один риск влияет на воздействие другого на проект.

Опишем случай двух невзаимодействующих рисков. Рассмотрим каждый риск отдельно, полагая, что у проекта существует только данный риск. Положим, что случайная величина X1 – это длительность проекта в случае возникновения дан- ного риска. Будем считать, что X1 – случайная величина непрерывного типа, то есть у нее, помимо функции распределения, также существует функция плотности распределения. Зная распределение X1, можно получить всю необходимую информацию о возможных значениях длительности проекта в случае возникновения только этого риска. В реальных проектах параметры распределения X1 обычно неизвестны. Более того, в различных проектах они тоже различны (в силу специфики организации работы, опыта разработчиков). Проблема нахождения вида распределения и его параметров может быть решена, если предположить, что существуют некоторые статистические данные о подобного рода рисках, которые проявили себя во время разработки предыдущих проектов, например: какая была длительность проекта в большинстве случаев из-за этого риска, максимальная длительность, минимальная длительность. Если такие данные есть, то в качестве параметров распределения случайной величины X1 можно использовать именно эти параметры. Далее будем полагать, что такие параметры известны.

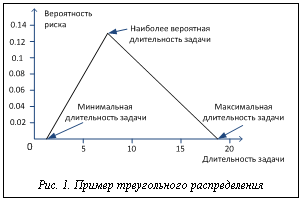
Пусть b, mp, w – минимальная (при отсутствии рисков), наиболее вероятная и максимальная длительности проекта в случае возникновения только этого риска. В качестве исходного неизвестного распределения предлагается использовать треугольное распределение, основанное на данных трех параметров (рис. 1).

Треугольное распределение достаточно часто используется в процессе моделирования случайных явлений при отсутствии достаточных данных, позволяющих сформулировать гипотезу об ином распределении. Точное аналитическое выражение для функции плотности треугольного распределения может быть рассчитано на основе трех известных параметров и условия нормирования.

Таким образом, выражение для функции плотности треугольного распределения в терминах введенных ранее параметров b, mp, w имеет вид

FX(x)=

Выражение для функции распределения имеет вид

FX(x)=

Если у проекта только один риск и при этом за основу взята модель, описанная выше, то совокупный риск будет иметь треугольное распределение. Если рисков больше, ситуация совершенно иная.

Для перехода к модели с n рисками следует принять предположение о том, что за каждый риск отвечает определенная группа людей. Таким образом, идет одновременная работа по каждому из рисков. Данное предположение позволяет сделать вывод, что в качестве случайной величины Z, соответствующей суммарной длительности проекта, может быть взята случайная величина, равная max(X1, X2, …, Xn), то есть итоговая длительность проекта будет равна максимальной из длительностей по всем рискам. Таким образом, итоговая задача построения совокупного риска проекта свелась к следующей задаче теории вероятностей.

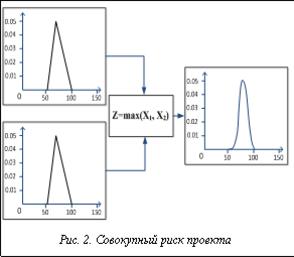Пусть X1, X2, …, Xn – независимые случайные величины, имеющие плотности распределения f1(x), f2(x), …, fn(x). Необходимо найти функцию распределения и функцию плотности распределения случайной величины Z=max(X1, X2, …, Xn).

Используя определение функции распределения из теории вероятностей, можно легко получить функцию распределения случайной величины Z. Функцией распределения данной величины будет функция FZ(z)=, где Fi(z) – функция распределения i-го риска (имеет вид, описанный выше). Функция плотности распределения fZ(z)=, где fj(z) – функция плотности распределения j-го риска.

График полученной функции распределения назовем диаграммой совокупного риска проекта (рис. 2), по которой можно сделать заключение о готовности проекта к заданной дате.

Достоинством данной модели является точность предсказания длительности проекта при корректной оценке исходных параметров риска, а недостатком – предположение о независимости и одновременности рисков, что не всегда верно.

Предложенная модель легла в основу метода управления рисками, апробированного при разработке ряда информационных систем для банковской сферы. Результат апробации позволил в 1,5 раза сократить случаи возникновения непредвиденных рисков в проектах разработки и тестирования ПО.

Литература

1.   Липаев В.В. Анализ и сокращение рисков проектов сложных программных средств. М.: Синтег, 2005. 224 с.

2.   Microsoft Solutions Framework. Дисциплина управления рисками MSF вер. 1.1. Техническое описание (white paper). URL: http://www.microsoft.com/msf (дата обращения: 13.02.2011).

3.   Липаев В.В. Процессы и стандарты жизненного цикла сложных программных средств: справочник. М.: Синтег, 2006. 276 с.

4.   ДеМарко Т., Листер Т. Вальсируя с медведями: управление рисками в проектах по разработке программного обеспечения. M.: Изд-во «p.m.Office», 2005. 196 c.