На современном этапе развития микроэлектроники формируется новое направление – создание на структурах «германий на изоляторе» высокоэффективных микросхем для сверхвысокопроизводительных вычислительных систем [1]. Во всех ведущих мировых исследовательских центрах ведутся поисковые исследования теоретических принципов моделирования, включая такой важный этап, как разработка аналитических моделей, применимых для схемотехнического моделирования [2] и проектирования сверхбольших интегральных схем (СБИС) на структурах «германий на изоляторе», а также разработка требований к технологии их изготовления [3].

Двухзатворные полевые транзисторы – одна из самых многообещающих архитектур для реализации рубежей, заявленных в новом направлении [1–4]. Двухзатворная архитектура обладает уникальными возможностями для масштабирования микросхем в наноразмерной области [2–6]. Она более гибкая, потому что по сравнению с традиционными планарными полевыми транзисторами больше параметров, таких как толщина рабочей области, толщина окиси фронтального и обратного затвора, легирование подложки, девиация затворных напряжений, могут быть использованы для оптимизации их физических характеристик. Она позволяет существенно уменьшить проявление таких короткоканальных эффектов (ККЭ), как roll-off порогового напряжения, DIBL-эффект и рост крутизны подпороговой характеристики. При этом следует учесть, что ККЭ эффективно подавляются в тонких пленках, формирующих транзисторную структуру.
Концепция транзистора «без перекрытия» затвора и стока/истока, которые сформированы в виде вытянутых областей, является одной из практически значимых из обширного семейства двухзатворных транзисторных архитектур [2, 5–7]. Кроме существущих преимуществ она имеет еще дополнительные степени свободы для оптимизации подавления ККЭ [6, 7] и представляет прак- тический интерес с позиции создания низко- вольтных нанотранзисторных СБИС с малой потребляемой мощностью. В настоящей работе в качестве прототипа транзисторной структуры «без перекрытия» (рис. 1) рассматривается аналогичная широко используемой структуре «кремний на изоляторе» (КНИ) с полностью обедненной рабочей областью, в которой кремний заменен на германий.
Отталкиваясь от апробированных подходов создания аналитических моделей двух затворных полевых КНИ нанотранзисторов, учитывающих основные физические характеристики [2, 6], в данной работе представлена 2D-аналитическая модель распределения потенциала в рабочей области транзистора выбранной архитектуры со структурой «германий на изоляторе». Численно исследованы поведение потенциала в зависимости от длины канала, толщины рабочей области и фронтального затвора, а также поведение таких ключевых характеристик транзистора, как пороговое напряжение и крутизна подпорогового наклона, где распределение потенциала играет решающую роль.
Распределение потенциала
Для нахождения равновесного распределения потенциала в анализируемой транзисторной структуре рассмотрим квазиклассическую задачу в рамках концепции зарядового разделения [3]. Отметим, что возможность использования данного приближения означает также и выбор начала отсчета потенциала j. В общем случае необходимо решать самосогласованную задачу, связанную с нахождением распределения 2D-потенциала рабочей области j(x, y), где оси x и y выбраны в соответствии с рисунком 1. 2D-уравнение Пуассона в рабочей области рассматриваемой структуры имеет вид
 (1)
(1)
где q – заряд электрона;  – диэлектрическая проницаемость германия; NA – концентрация легирования рабочей области; Lg – длина затвора;
– диэлектрическая проницаемость германия; NA – концентрация легирования рабочей области; Lg – длина затвора; 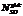 – максимальная концентрация легирования областей стока и истока;
– максимальная концентрация легирования областей стока и истока;  – параметр, определяющий крутизну гауссова профиля примеси в областях стока и истока вдоль оси х; g – градиент легирования областей стока и истока; h – масштабный фактор, характеризующий отношение длин зазора и затвора h = Ls/Lg, со следующими граничными условиями:
– параметр, определяющий крутизну гауссова профиля примеси в областях стока и истока вдоль оси х; g – градиент легирования областей стока и истока; h – масштабный фактор, характеризующий отношение длин зазора и затвора h = Ls/Lg, со следующими граничными условиями:
 ,
,
 ,
,
j(0, y)= Ubi,
j(Leff, y) = j(0, y) + Uds,
где tGe – толщина рабочей области транзистора; Leff – эффективная длина канала; Cf – емкость фронтального затвора; Cb – емкость обратного затвора; Uf – напряжение на фронтальном затворе; Ub – напряжение на обратном затворе;  – напряжение плоских зон на фронтальном затворе;
– напряжение плоских зон на фронтальном затворе;  – напряжение плоских зон на обратном затворе; Ubi – встроенная разность потенциалов; Uds – напряжение сток-исток.
– напряжение плоских зон на обратном затворе; Ubi – встроенная разность потенциалов; Uds – напряжение сток-исток.
Отметим, что последнее граничное условие действует при x=Leff , а не Lg, как для приборов с крутым (близким к вертикальному) профилем областей стока и истока. Эффективная длина канала, включающая вклад вытянутых областей стока и истока к длине затвора, моделируется выражением  c тремя компонентами: Lg, h и g, последний из которых выражается через параметры s и zSD. Коэффициент 2 вытекает из симметричности рассматриваемой транзисторной структуры (наличие одинаковых по форме областей стока и истока). Выражение
c тремя компонентами: Lg, h и g, последний из которых выражается через параметры s и zSD. Коэффициент 2 вытекает из симметричности рассматриваемой транзисторной структуры (наличие одинаковых по форме областей стока и истока). Выражение  определяет согласование распределения концентрации вытянутых областей стока и истока и канальной длины и, соответственно, их вклад в эффективную длину канала, где zSD = 2,25´1019ln(h)+1,5´1019определяет уровень легирования областей стока и истока, при котором экстрагируется значение эффективной длины Leff. Отношение Lg/Ls в zSD подчеркивает, что для больших зазоров (h>1) фронтальный затвор фактически не влияет на области стока и истока. В геометрическом приближении вклад областей стока и истока в величину параметра Leff можно представить как расстояние от края затвора до некоторой точки на границе легирования стока/истока. Это аппроксимируется через параметр zSD в выражении для Leff, то есть пограничный уровень легирования определяется через параметр эффективного сток/исток-уровня легирования zSD. Следует отметить, что аналитическое выражение для Leff хорошо согласуется с эффективной длиной, экстрагированной из результатов численного 2D-моделирования.
определяет согласование распределения концентрации вытянутых областей стока и истока и канальной длины и, соответственно, их вклад в эффективную длину канала, где zSD = 2,25´1019ln(h)+1,5´1019определяет уровень легирования областей стока и истока, при котором экстрагируется значение эффективной длины Leff. Отношение Lg/Ls в zSD подчеркивает, что для больших зазоров (h>1) фронтальный затвор фактически не влияет на области стока и истока. В геометрическом приближении вклад областей стока и истока в величину параметра Leff можно представить как расстояние от края затвора до некоторой точки на границе легирования стока/истока. Это аппроксимируется через параметр zSD в выражении для Leff, то есть пограничный уровень легирования определяется через параметр эффективного сток/исток-уровня легирования zSD. Следует отметить, что аналитическое выражение для Leff хорошо согласуется с эффективной длиной, экстрагированной из результатов численного 2D-моделирования.
Для моделирования анализируемых транзисторных структур начало координат (0; 0) для х и у (как правило, это край затвора для классических структур с вертикальными областями стока и истока) приемлемо сдвинуть на расстояние ±z от края затвора. Эта позиция начала координат зависит от значений h и g. Сдвиг от затвора в область стока будет возрастать для больших h и малых g. Следовательно, DL = Leff – Lg > 0 при z > 0, тогда как отрицательные значения z < 0 показывают, что начало координат (точка отсчета) располагается под затвором (в направлении к стоку) и как результат DL < 0.
Решение уравнения Пуассона (1) в общем случае аналитически невозможно. Одним из путей решения является предположение о характере распределения потенциала в рабочей области. С учетом вышеизложенных приближений, в частности, исключения из рассмотрения второго и третьего членов в правой части, допустимо применить принцип суперпозиции для потенциала, то есть разделить 2D-потенциал на два [6, 8]. Один соответствует длинноканальному случаю. Второй определяется ККЭ. Распределением первого потенциала j(1D)(y) является решение 1D-уравнения Пуассона. Распределение второго потенциала j(2D)(x, y) вытекает из решения 2D-уравнения Лапласа. Тогда обобщенный потенциал можно представить в виде
j(x, y) = j(1D)(y) + j(2D)(x, y), (2)
где  ;
;
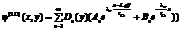 ;
;
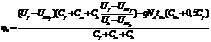 ;
;



 ,
,
где граничные условия для уравнения Лапласа можно представить в виде j(2D)(0, y) = Ubi – jsf (y) и j(2D)(Leff, y) = Ubi + Ubs – jsf (y); jsf – фронтальный поверхностный потенциал; CGe – емкость рабочей области; An, Bn, Dn – нормировочные коэффициенты; ln – собственные значения.
В рассматриваемом случае, следуя [7], характеристическое уравнение для собственных значений запишем, например, в виде
 . (3)
. (3)
С собственными значениями связана характеристическая длина l, которая, как известно, в модельных представлениях является индикатором проявления ККЭ в рассматриваемых транзисторных структурах [4]. Их связь определяется выражением  [8].
[8].
Численно рассчитанные зависимости харак- теристической длины от толщины рабочей об- ласти и фронтального затвора приведены на рисунке 2.
Характеристическая длина является функцией толщин пленок, формирующих канальную область транзистора. В идеальном случае для полного подавления ККЭ должно быть выполнено условие Leff / l >> 1. Варьированием значений градиента и зазора достигается модуляция эффективной длины канала Leff, а варьированием толщины фронтального затвора tf и толщины рабочей области tGe реализуется изменение характеристической длины l. В итоге получаем четыре степени свободы для минимизации ККЭ. Считается, что для схемотехнических приложений условие эффективного подавления ККЭ сводится к виду Leff /l >2 [9].
 Следуя методике, рассмотренной в [7], по двум данным зависимостям (рис. 2) можно определить собственное значение для любой комбинации tGe, tf из области допустимых значений по правилу l = l(tGe)l(tf). Опираясь на результаты из работ [7, 9] и на рисунок 2, можно оценить степень проявления ККЭ при использовании различных материалов, формирующих транзисторную структуру. В случаях, когда значения толщины близки к предельным, наименее уязвимой от проявления ККЭ является традиционная структура КНИ. Так, например, при толщине рабочей области 5 нм и толщине фронтального затвора 1 нм значение характеристической длины составляет 9,9 нм, для структуры «германий на изоляторе» – 12,6 нм и для КНИ с фронтальным затвором окиси гафния – 13,3 нм. С точки зрения создания высокоэффективных микросхем переход на германий более перспективен по сравнению со структурами КНИ с фронтальным затвором из окиси гафния. Поскольку с учетом условия Leff /l >2 из предыдущего абзаца в структурах «германий на изоляторе» ККЭ будут проявляться при меньших длинах затвора, в совокупности с более высокой подвижностью это обусловит выигрыш в быстродействии и рассеиваемой мощности [1, 3].
Следуя методике, рассмотренной в [7], по двум данным зависимостям (рис. 2) можно определить собственное значение для любой комбинации tGe, tf из области допустимых значений по правилу l = l(tGe)l(tf). Опираясь на результаты из работ [7, 9] и на рисунок 2, можно оценить степень проявления ККЭ при использовании различных материалов, формирующих транзисторную структуру. В случаях, когда значения толщины близки к предельным, наименее уязвимой от проявления ККЭ является традиционная структура КНИ. Так, например, при толщине рабочей области 5 нм и толщине фронтального затвора 1 нм значение характеристической длины составляет 9,9 нм, для структуры «германий на изоляторе» – 12,6 нм и для КНИ с фронтальным затвором окиси гафния – 13,3 нм. С точки зрения создания высокоэффективных микросхем переход на германий более перспективен по сравнению со структурами КНИ с фронтальным затвором из окиси гафния. Поскольку с учетом условия Leff /l >2 из предыдущего абзаца в структурах «германий на изоляторе» ККЭ будут проявляться при меньших длинах затвора, в совокупности с более высокой подвижностью это обусловит выигрыш в быстродействии и рассеиваемой мощности [1, 3].
На рисунке 3 приведены результаты расчетов латерального (вдоль канала) распределения фронтального поверхностного потенциала для двух прототипов транзисторов n-типа, отвечающих вышеизложенным требованиям со следующими параметрами: для типа 1 Lg = 45 нм, tGe = 10 нм, tf = 2,2 нм, tb = 100 нм; для типа 2 Lg = 32 нм, tGe = 8 нм, tf = 1,6 нм, tb = 100 нм.
 Как следует из представленных данных, уменьшение эффективной длины канала приводит к повышению потенциала в результате модуляции длины канала. Поскольку расширение области пространственного заряда вокруг стока и истока жестко зависит от размерностей устройства, вклад областей пространственного заряда вокруг стока и истока становится значительным в более тонком устройстве с более коротким каналом.
Как следует из представленных данных, уменьшение эффективной длины канала приводит к повышению потенциала в результате модуляции длины канала. Поскольку расширение области пространственного заряда вокруг стока и истока жестко зависит от размерностей устройства, вклад областей пространственного заряда вокруг стока и истока становится значительным в более тонком устройстве с более коротким каналом.
На рисунке 4 приведены результаты расчетов распределения потенциала по глубине рабочей области (вдоль оси y) для тех же прототипов.
 При подаче смещения на обратный затвор происходит перераспределение концентрации носителей в рабочей области. При положительном смещении в ней преобладают электроны, при отрицательном – дырки. (В идеальном случае рабочая область будет полностью обедненной.) В любом случае это является причиной своеобразной экранировки электрического поля в рабочей области. И, как следствие, поверхностный фронтальный потенциал практически не изменяется. Варьирование напряжения на обратном затворе в значительных пределах приводит только к изменению степени экранировки, а поверхностный потенциал практически остается постоянным.
При подаче смещения на обратный затвор происходит перераспределение концентрации носителей в рабочей области. При положительном смещении в ней преобладают электроны, при отрицательном – дырки. (В идеальном случае рабочая область будет полностью обедненной.) В любом случае это является причиной своеобразной экранировки электрического поля в рабочей области. И, как следствие, поверхностный фронтальный потенциал практически не изменяется. Варьирование напряжения на обратном затворе в значительных пределах приводит только к изменению степени экранировки, а поверхностный потенциал практически остается постоянным.
Пороговое напряжение
 В квазиклассическом приближении допустимо считать, что пороговое напряжение Uth – это затворное напряжение, при котором минимальная индуцированная плотность инверсионных зарядов достигает некоторого значения Qth, обеспечивающего генерацию канала [6]. Данное положение можно представить выражением
В квазиклассическом приближении допустимо считать, что пороговое напряжение Uth – это затворное напряжение, при котором минимальная индуцированная плотность инверсионных зарядов достигает некоторого значения Qth, обеспечивающего генерацию канала [6]. Данное положение можно представить выражением
 , (4)
, (4)
где ni – индуцированная плотность носителей в канале; jmin – минимум потенциала в рабочей области.
Результаты моделирования для анализируемых устройств, приведенные на рисунке 5, иллюстрируют зависимость Uth от различных значений h.
Нелинейный характер полученных зависимостей обусловлен тем, что зависимость концентрации носителей от уровня потенциала в рабочей области в общем случае имеет экспоненциальный характер, а распределение потенциала, в свою очередь, существенно зависит от совокупности параметров, в частности l, h, g.
Приведенные результаты позволяют оценить диапазон изменения порогового напряжения при переходе от одних топологических параметров к другим. В общем случае с уменьшением зазора пороговое напряжение Uth понижается. Снижение h определяет возрастание влияния ККЭ, которое вызывает характерное изменение Uth. Причем эффект roll-off для больших зазоров (h > 1) практически не проявляется. Для h < 1 и больших g придется прибегнуть к масштабированию толщин транзисторной структуры. Большие значения h приводят к значениям Uth, которые почти не зависят от h и слабо зависят от g. В анализируемом диапазоне абсолютная величина снижения порогового напряжения (DUth) для первого прототипа составляет 49 мВ, для второго DUth =74 мВ. Следовательно, в соответствии с критерием проявления ККЭ в рассматриваемых транзисторах ККЭ не будут проявляться.
Подпороговый наклон
Из анализа распределения потенциала можно получить приемлемую оценку величины наклона подпороговой характеристики. Предположим, что подпороговый наклон (S-наклон) связан с концентрацией носителей в точке минимума потенциала и, следовательно, с самим потенциалом jmin, тогда S-наклон может быть получен как
 ,(5)
,(5)
где nmin – концентрация носителей в точке минимума потенциала; k – постоянная Больцмана; T – температура.
Этот подход для оценки S-наклона широко использовался в нескольких предшествующих работах [4, 6, 7, 10]. Результаты моделирования исследуемого прототипа транзистора 2, приведенные на рисунке 6, иллюстрируют зависимость параметра S от различных значений h, g.
 Из результатов расчетов следует, что подпороговый наклон, близкий к теоретическому пределу, достигается только для случая градиента легирования 2 нм/дек. и h ³ 1. Тогда как при превышении максимально высоких значений g возрастание величины S-наклона характеризуется неярко выраженной нелинейной зависимостью. В области h ³ 1 для рассматриваемого диапазона градиентов легирования значение подпорогового наклона практически не зависит от h. Для h < 1 зависимость S(h) круто возрастает, начиная с некоторого значения h, характерного для конкретного значения g. Например, для g = 2 нм/дек. h = 0,62, для g = 3 нм/дек. h = 0,74, для g = 4 нм/дек. h = 0,84.
Из результатов расчетов следует, что подпороговый наклон, близкий к теоретическому пределу, достигается только для случая градиента легирования 2 нм/дек. и h ³ 1. Тогда как при превышении максимально высоких значений g возрастание величины S-наклона характеризуется неярко выраженной нелинейной зависимостью. В области h ³ 1 для рассматриваемого диапазона градиентов легирования значение подпорогового наклона практически не зависит от h. Для h < 1 зависимость S(h) круто возрастает, начиная с некоторого значения h, характерного для конкретного значения g. Например, для g = 2 нм/дек. h = 0,62, для g = 3 нм/дек. h = 0,74, для g = 4 нм/дек. h = 0,84.
Физические ограничения: деградация ширины запрещенной зоны
Как известно, германий характеризуется более узкой (примерно в 2 раза) запрещенной зоной, чем кремний. В процессе формирования транзисторной структуры будут проявляться особенности, связанные с атомной структурой германия. В частности, так называемые качающиеся связи [11] образуют в запрещенной зоне дополнительные энергетические уровни. К такому же результату может привести процесс легирования. Рассмотрим, как будет влиять присутствие дискретных уровней в запрещенной зоне на ее ширину. Исследуем простую модельную задачу, когда в запрещенной зоне по три дискретных энергетических уровня с энергиями E1, E2, E3 и энергиями E4, E5, E6 симметрично расположены вблизи потолка и дна запрещенной зоны. Распределение состояний в разрешенных зонах определяется следующими соотношениями: Nss(Ei) = Nc при E>Ec, Nss(Ei) = 0 при Ec >E>Ev, Nss(Ei) = Nv при E
Определим зависимость изменения ширины запрещенной зоны в этом случае. Энергетическое положение краев запрещенной зоны вытекает из решения следующего трансцендентного уравнения:
 , (6)
, (6)
где Nk – значение плотности состояний, соответствующее энергии краев запрещенной зоны и примесных уровней.
Таким образом, ширина запрещенной зоны при заданной температуре Eg(T) определяется выражением Eg(T) = Ec(T) – Ev(T), а ее изменение DEg(T) соотношением DEg(T) = dEc(T) – dEv(T).
На рисунке 7 приведены результаты расчетов изменения ширины запрещенной зоны в идеальном случае и с учетом дискретных уровней в запрещенной зоне в диапазоне температур 200, …, 800 К. Как следует из представленных данных, в идеальном случае изменение ширины запрещенной зоны имеет линейный характер. При наличии в запрещенной зоне дополнительных дискретных энергетических уровней в области низких температур исследуемая зависимость отклоняется от линейной. Причем этот диапазон наиболее интересен разработчикам микросхем.
Полученные модельные представления качественно согласуются с экспериментальными результатами. Как отмечено в [12], полученные при оптических измерениях экспериментальные значения Eg(T) зависят от методики их определения. Сравнение теории с экспериментами других работ, взятых из [12], тоже дают хорошие резуль- таты. При сравнении теории и эксперимента не- обходимо учитывать, что значения ширины запрещенной зоны, определенные по температурной зависимости электропроводности и по измерениям спектральных зависимостей поглощения света, могут различаться. При сравнении теории и эксперимента особое внимание следует обратить на область низких температур, где изгиб зависимости Eg(T) обусловлен присутствием дополнительных уровней в запрещенной зоне. В общем случае величина и форма изгиба Eg(T) зависят от формы и вида плотности состояний Nss(Ei) как в разрешенных зонах, так и в запрещенной зоне. Очевидно и то, что причиной рассогласования экспериментальных зависимостей и теоретической является отличие истинной плотности состояний от плотности состояний модели.
 В заключение отметим, что в работе рассмотрен один из возможных подходов к разработке 2D-аналитической модели распределения потенциала в рабочей области полевого двухзатворного нанотранзистора со структурой «германий на изоляторе» и архитектурой «без перекрытия областей затвора и стока/истока». Получено аналитическое решение уравнения Пуассона с использованием принципа суперпозиции для потенциала.
В заключение отметим, что в работе рассмотрен один из возможных подходов к разработке 2D-аналитической модели распределения потенциала в рабочей области полевого двухзатворного нанотранзистора со структурой «германий на изоляторе» и архитектурой «без перекрытия областей затвора и стока/истока». Получено аналитическое решение уравнения Пуассона с использованием принципа суперпозиции для потенциала.
Сформулированы критерии оптимизации технологических параметров исследуемых транзисторных структур для эффективного подавления ККЭ. Показано, что в анализируемых устройствах ККЭ проявляются в большей степени, чем в аналогичных структурах КНИ.
На основе полученных численных решений уравнения Пуассона проанализирована зависимость от технологических параметров ряда основных электрофизических характеристик, таких как распределение потенциала в рабочей области, порогового напряжения и крутизны подпороговой характеристики.
Так, при масштабировании потенциал в рабочей области возрастает в результате уменьшения эффективной длины канала. Поскольку расширение области пространственного заряда вокруг стока и истока жестко зависит от размерностей устройства, вклад областей пространственного заряда вокруг стока и истока становится значительным в более тонком устройстве с более коротким каналом.
Технологические параметры транзисторной структуры позволяют эффективно управлять рассматриваемыми ключевыми характеристиками, такими как пороговое напряжение и крутизна подпороговой характеристики.
Литература
1. International technology roadmap for semiconductors, 2012 ed. URL: http://public.itrs.net/International technology roadmap for semiconductor 2012 edition (дата обращения: 17.10.2012).
2. Масальский Н.В. Проблемы схемотехнического моделирования нанотранзисторов со структурой «кремний на изоляторе» // Программные продукты и системы. 2013. № 4. С. 60–67.
3. Shang H., Frank M.M., Gusev E.P., Chu J.O., Bedell S.W., Guarini K.W., Ieong M. Germanium channel MOSFETs: opportunities and challenges. IBM J. Res. Develop, 2006, vol. 50, no. 4, pp. 377–386.
4. Colinge J.-P. Silicon Insulator Technology: Materials to VLSI. Кluwer Acad. Publ., Boston, Dordrecht, London, 1997.
5. Kawamoto A., Sato S., Omura Y. Engineering S/D diffusion for sub-100-nm channel SOI MOSFETs. IEEE Trans Electron Devices, 2004, vol. 51, pp. 907–913.
6. Kranti A., Armstrong G. Engineering source/drain extension regions in nanoscale double gate (DG) SOI MOSFETs: Analytical model and design considerations. Solid-State Electronics. 2006, vol. 50, no. 2, pp. 437–447.
7. Masalsky N.V. Optimization of Parameters of Double-Gate Sub-20 Nanometers SOI CMOS Transistors with Architecture “without Overlapping”. Russian Microelectronics, 2012, vol. 41, no. 1, pp. 51–58.
8. Liang X., Yaur. A 2-D Analytical Solution for SCEs in DG MOSFETs. IEEE Trans Electron. 2004, vol. 51, pp. 1385–1391.
9. Масальский Н.В. Синтез характеристик логических вентилей на двух затворных суб-25 нм КНИ КМОП транзисторах для маломощных применений // Нано- и микросистемная техника. 2010. Т. 118. № 5. С. 41–46.
10. Chen Q., Agrawal B., Meindl J.D. A comprehensive analytical subthreshold swing (S) model for double-gate MOSFETs. IEEE Trans Electron Devices, 2002, vol. 49, no. 6, pp. 1086–1090.
11. Segev D., Janotti A., van de Walle C. Self-consistent band-gap corrections in density functional theory using modified pseudopotentials. Physical Review B, 2007, vol. 75, pp. 035201_1–035201_9.
12. Емельянов А.М. Определение изменений ширины запрещений зоны непрямозонных полупроводников по спектрам краевой люминесценции // Письма в ЖТФ. 2009. Т. 35. № 6. С. 9–16.
References
1. International technology roadmap for semiconductors, 2012 ed. Available at: http://public.itrs.net/ (accessed May 27,
2014).
2. Masalsky N.V. Nanotransistors circuitry simulation problems with silicon-on-insulator structure. Programmnye
produkty i sistemy [Software & Systems]. 2013, no. 4, pp. 60–67 (in Russ.).
3. Shang H., Frank M.M., Gusev E.P., Chu J.O., Bedell S.W., Guarini K.W., Ieong M. Germanium channel MOSFETs:
opportunities and challenges. IBM J. Res. Develop. 2006, vol. 50, no. 4, pp. 377–386.
4. Colinge J.-P. Silicon Insulator Technology: Materials to VLSI. Кluwer Acad. Publ., Boston, Dordrecht, London,
1997.
5. Kawamoto A., Sato S., Omura Y. IEEE Trans Electron Devices. 2004, vol. 51, pp. 907–913.
6. Kranti A., Armstrong G. Engineering source/drain extension regions in nanoscale double gate (DG) SOI MOSFETs:
Analytical model and design considerations. Solid-State Electronics. 2006, vol. 50, no. 2, pp. 437–447.
7. Masalsky N.V. Optimization of Parameters of Double-Gate Sub-20 Nanometers SOI CMOS Transistors with
Architecture “without Overlapping”. Russian Microelectronics. 2012, vol. 41, no. 1, pp. 51–58.
8. Liang X., Yaur A. A 2-D Analytical Solution for SCEs in DG MOSFETs. IEEE Trans Electron. 2004, vol. 51, pp.
1385–1391.
9. Masalsky N.V. Design of logic gate characteristics for double gate sub-25 nm SOI CMOS transistors for lower power
applications. Nano- i mikrosistemnaya tekhnika [Journ. of Nano and Microsystem Technique]. 2010, vol. 118, no. 5,
pp. 41–46 (in Russ.).
10. Chen Q., Agrawal B., Meindl J.D. A comprehensive analytical subthreshold swing (S) model for double-gate
MOSFETs. IEEE Trans Electron Devices. 2002, vol. 49, no. 6, pp. 1086–1090.
11. Segev D., Janotti A., van de Walle C. Self-consistent band-gap corrections in density functional theory using
modified pseudopotentials. Physical Review B. 2007, vol. 75, pp. 035201_1–035201_9.
12. Emelyanov A.M. Pisma v ZHTF [Applied Physics Letters]. 2009, vol. 35, no. 6, pp. 9–16 (in Russ.).




 (1)
(1) – диэлектрическая проницаемость германия; NA – концентрация легирования рабочей области; Lg – длина затвора;
– диэлектрическая проницаемость германия; NA – концентрация легирования рабочей области; Lg – длина затвора; 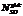 – максимальная концентрация легирования областей стока и истока;
– максимальная концентрация легирования областей стока и истока;  – параметр, определяющий крутизну гауссова профиля примеси в областях стока и истока вдоль оси х; g – градиент легирования областей стока и истока; h – масштабный фактор, характеризующий отношение длин зазора и затвора h = Ls/Lg, со следующими граничными условиями:
– параметр, определяющий крутизну гауссова профиля примеси в областях стока и истока вдоль оси х; g – градиент легирования областей стока и истока; h – масштабный фактор, характеризующий отношение длин зазора и затвора h = Ls/Lg, со следующими граничными условиями: ,
, ,
, – напряжение плоских зон на фронтальном затворе;
– напряжение плоских зон на фронтальном затворе;  – напряжение плоских зон на обратном затворе; Ubi – встроенная разность потенциалов; Uds – напряжение сток-исток.
– напряжение плоских зон на обратном затворе; Ubi – встроенная разность потенциалов; Uds – напряжение сток-исток. c тремя компонентами: Lg, h и g, последний из которых выражается через параметры s и zSD. Коэффициент 2 вытекает из симметричности рассматриваемой транзисторной структуры (наличие одинаковых по форме областей стока и истока). Выражение
c тремя компонентами: Lg, h и g, последний из которых выражается через параметры s и zSD. Коэффициент 2 вытекает из симметричности рассматриваемой транзисторной структуры (наличие одинаковых по форме областей стока и истока). Выражение  определяет согласование распределения концентрации вытянутых областей стока и истока и канальной длины и, соответственно, их вклад в эффективную длину канала, где zSD = 2,25´1019ln(h)+1,5´1019определяет уровень легирования областей стока и истока, при котором экстрагируется значение эффективной длины Leff. Отношение Lg/Ls в zSD подчеркивает, что для больших зазоров (h>1) фронтальный затвор фактически не влияет на области стока и истока. В геометрическом приближении вклад областей стока и истока в величину параметра Leff можно представить как расстояние от края затвора до некоторой точки на границе легирования стока/истока. Это аппроксимируется через параметр zSD в выражении для Leff, то есть пограничный уровень легирования определяется через параметр эффективного сток/исток-уровня легирования zSD. Следует отметить, что аналитическое выражение для Leff хорошо согласуется с эффективной длиной, экстрагированной из результатов численного 2D-моделирования.
определяет согласование распределения концентрации вытянутых областей стока и истока и канальной длины и, соответственно, их вклад в эффективную длину канала, где zSD = 2,25´1019ln(h)+1,5´1019определяет уровень легирования областей стока и истока, при котором экстрагируется значение эффективной длины Leff. Отношение Lg/Ls в zSD подчеркивает, что для больших зазоров (h>1) фронтальный затвор фактически не влияет на области стока и истока. В геометрическом приближении вклад областей стока и истока в величину параметра Leff можно представить как расстояние от края затвора до некоторой точки на границе легирования стока/истока. Это аппроксимируется через параметр zSD в выражении для Leff, то есть пограничный уровень легирования определяется через параметр эффективного сток/исток-уровня легирования zSD. Следует отметить, что аналитическое выражение для Leff хорошо согласуется с эффективной длиной, экстрагированной из результатов численного 2D-моделирования. ;
;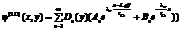 ;
;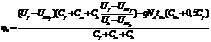 ;
;


 ,
, . (3)
. (3) [8].
[8].



 , (4)
, (4) ,(5)
,(5)
 , (6)
, (6)
