Метод управления со скользящим режимом (СР) разработан в конце 1950-х годов [1], а к концу 1970-х был признан одним из наиболее перспективных и надежных методов управления [2]. Тем не менее первые реализации управления на основе СР показали, что реальный СР порождает колебания, устранение которых является главной проблемой при использовании данной техники управления [3].
В середине 1980-х годов были предложены следующие три основных подхода по устранению колебаний в системе СР.
· Использование насыщенности управления вместо разрывного управления [4]. Такой подход позволяет управлять непрерывно, но не может держать динамику системы в пределах на поверхности переключения. Это только обеспечивает сходимость к пограничному слою скользящего многообразия, размер которого определяется по наклону характеристики насыщения.
· Наблюдательный подход [5]. Сводит проблему робастного управления к проблеме точной робастной оценки и, следовательно, может привести к ухудшению робастности по отношению к объекту в связи с несоответствием наблюдателя и динамики объекта [3].
· СР высокого порядка. Позволяет за конечное время сойтись к нулю не только скользящей переменной, но и ее производным. Теоретически скользящие режимы n-го порядка будут полностью подавлять колебания в модели системы (но не в физической системе), когда в модели объекта присутствуют исполнительные устройства и датчики. Однако данным способом эффект колебаний не может быть предотвращен [6].
Отмеченная проблема может быть решена с помощью технологии интеллектуальных вычислений на основе технологии мягких вычислений с использованием ряда важных термодинамических, информационно-энтропийных и динамических критериев управления.
В статье описана разработка нечеткого регулятора (НР) с помощью нового интеллектуального инструментария – оптимизатора баз знаний (ОБЗ), который позволит устранить возникающие при управлении СР колебания, используя технологию мягких вычислений.
Скользящий режим управления. Динамическое поведение НР характеризуется множеством лингвистических правил, составленных экспертом. Пользуясь этим множеством, механизм вывода выдает соответствующее управляющее воздействие. Для двухмерного случая нечеткое управление [7] может использовать ошибку (e) и скорость изменения ошибки ( ) как входные лингвистические переменные нечеткого правила (см. табл.).
) как входные лингвистические переменные нечеткого правила (см. табл.).
Нечеткие правила
Fuzzy rules
|
e ̇
|
e
|
|
NB
|
NM
|
NS
|
Z
|
PS
|
PM
|
PB
|
|
PB
|
Z
|
NZ
|
NS
|
NM
|
NB
|
NB
|
NB
|
|
PM
|
PZ
|
Z
|
NZ
|
NS
|
NM
|
NB
|
NB
|
|
PS
|
PS
|
PZ
|
Z
|
NZ
|
NS
|
NM
|
NB
|
|
Z
|
PM
|
PS
|
PZ
|
Z
|
NZ
|
NS
|
NM
|
|
NS
|
PB
|
PM
|
PS
|
PZ
|
Z
|
NZ
|
NS
|
|
NM
|
PB
|
PB
|
PM
|
PS
|
PZ
|
Z
|
NZ
|
|
NB
|
PB
|
PB
|
PB
|
PM
|
PS
|
PZ
|
Z
|
В таблице использованы следующие обозначения: P – positive (положительный), N – negative (отрицательный), Z – zero (ноль), B – big (большой), S – small (малый), M – medium (средний).

 Другой способ рассмотрения правил – фазовая траектория (см. рис. 1, стрелки показывают направление усиления, Z – поверхность переключения).
Другой способ рассмотрения правил – фазовая траектория (см. рис. 1, стрелки показывают направление усиления, Z – поверхность переключения).
Из таблицы можно заключить следующее: если e и  близки к поверхности, то нечеткое управляющее воздействие сильное, а чем дальше оно от поверхности, тем слабее. Поэтому поверхность скольжения принимает вид
близки к поверхности, то нечеткое управляющее воздействие сильное, а чем дальше оно от поверхности, тем слабее. Поэтому поверхность скольжения принимает вид 
 , где w – положительная переменная, определяющая скорость сходимости для e и
, где w – положительная переменная, определяющая скорость сходимости для e и  .
.
Структура интеллектуальной системы управления (ИСУ) для регулятора с СР показана на рисунке 2.
На вход блока вычислений s и s’ подается текущая ошибка управления (вычисляется как разность состояния объекта управления и задающего сигнала) и скорость ошибки управления, после этого полученные значения поступают на вход НР, который выдает управляющее воздействие на объект управления [8].
Математическая модель системы. В качестве примера применения ОБЗ рассмотрим задачу управления неустойчивой динамической системой «движущаяся каретка–перевернутый маятник» (рис. 3).
 Динамическое поведение этой системы при воздействии силы управления u описывается системой дифференциальных уравнений второго порядка:
Динамическое поведение этой системы при воздействии силы управления u описывается системой дифференциальных уравнений второго порядка:
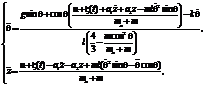 (1)
(1)
где z и q – обобщенные координаты; g – ускорение свободного падения 9,8 м/сек.2; mc – масса тележки; m – масса перевернутого маятника (называемого «шест»); l – половина длины маятника; k и a1 – коэффициенты трения в z и q соответственно; a2 – сила упругости тележки; z(t) – внешний стохастический шум.

 Без управления маятник невозможно удержать в вертикальном положении [4]. Цель управления – сбалансировать положение маятника в условиях существенных ограничений на скорость и положение тележки, а также ограниченной силы управления. В этом случае для стабилизации необходимо выполнение условия q = 0. Рассмотрим модель динамической системы cо следующими параметрами: mc = 1,0 кг; m = 0,1 кг; l = 0,5 м; коэфф. трения в θ, k = 0,4; коэфф. трения в z, a2 = 0,1; сила упругости, a1 = 5,0 и следующими начальными условиями: [q0
Без управления маятник невозможно удержать в вертикальном положении [4]. Цель управления – сбалансировать положение маятника в условиях существенных ограничений на скорость и положение тележки, а также ограниченной силы управления. В этом случае для стабилизации необходимо выполнение условия q = 0. Рассмотрим модель динамической системы cо следующими параметрами: mc = 1,0 кг; m = 0,1 кг; l = 0,5 м; коэфф. трения в θ, k = 0,4; коэфф. трения в z, a2 = 0,1; сила упругости, a1 = 5,0 и следующими начальными условиями: [q0 ]=[10 0,1](grad); [z0
]=[10 0,1](grad); [z0 ]=[00].
]=[00].
Проектирование регулятора с СР в инструментарии ОБЗ. Для создания НР в ОБЗ получен ОС на ситуации с внешними воздействиями (шум с распределением Гаусса).
На рисунке 4 показаны спроектированные с помощью ОБЗ функции принадлежности.
Сравнение результатов моделирования. Будем рассматривать модель динамической системы c параметрами: µc = 1,0 кг, µ = 0,1 кг, l = 0,5 м, коэфф. трения в θ, k = 0,4, коэфф. трения в z, a2= 0,1, сила упругости, a1=5,0 и следующими начальными условиями: [q0  ]=[10 0,1](grad); [z0
]=[10 0,1](grad); [z0 ]=[00]. Весовой параметр w=5,9.
]=[00]. Весовой параметр w=5,9.
Сравним базу, спроектированную в ОБЗ, с базой, спроектированной в ANFIS (встроенный инструментарий Матлаб) [9, 10], и ПИД-регулятором (рис. 5).
Р езультаты моделирования показали, что только интеллектуальный регулятор, спроектированный с помощью ОБЗ, является робастным. Именно он выполнил поставленную задачу управления.
езультаты моделирования показали, что только интеллектуальный регулятор, спроектированный с помощью ОБЗ, является робастным. Именно он выполнил поставленную задачу управления.
Таким образом, отметим, что рассмотрен скользящий режим управления для неустойчивой динамической системы «каретка–перевернутый маятник» и представлена интеллектуальная структура управления системы со скользящим режимом управления. Сравнивается работа спроектированных регуляторов с помощью эксперта (FIS), системы нечеткого вывода ANFIS и интеллектуального инструментария ОБЗ для неустойчивой динамической системы.
Результаты моделирования динамического поведения рассматриваемого объекта управления «каретка–перевернутый маятник» показали эффективность и робастность спроектированного с помощью ОБЗ нечеткого регулятора даже в непредвиденных условиях управления.
Новый разработанный инструментарий ОБЗ может строить робастные интеллектуальные системы управления, способные функционировать как на множестве обучающих (типовых), так и на классе новых (непредвиденных) ситуаций управления для систем, использующих скользящий режим управления.
Литература
1. Utkin V.I. First Stage of VSS: people and events. In Lecture Notes in Control and Information Science, London, UK, Springer-Verlag, 2002, vol. 274, pp. 1–33.
2. Utkin V.I. Sliding Modes and Their Application in Variable Structure Systems. Moscow, Mir Publ., 1978.
3. Young K.D., Utkin V.I., and Ozguner U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol., 1999, vol. 7, no. 3, pp. 328–342.
4. Slotine J.J. and Li W. Applied Nonlinear Control. Englewood Cliffs, NJ, USA, Prentice Hall Publ., 1991.
5. Bondarev A.G., Bondarev S.A., Kostylyeva N.Y., and Utkin V.I. Sliding modes in systems with asymptotic state observers. Automatica i telemechanica (Autom. Remote Control), 1985, vol. 46, no. 5, pp. 679–684.
6. Bartolini G., Fridman L., Pisano A. Modern sliding mode control theory. Springer Verlag, 2008. 7. Shien M. Switching-type fuzzy sliding mode control of a cart-pole system. Mechatronics, vol. 10.
8. Литвинцева Л.В., Ульянов С.В., Ульянов С.С. Построение робастных баз знаний нечетких регуляторов для интеллектуального управления существенно нелинейными динамическими системами. Ч. II // Изв. РАН. ТиСУ. 2006. № 5.
9. Jang J.S. Neuro-Fuzzy and Soft Computing. NJ, USA, Prentice Hall Publ., 1997, pp. 335–368. 10. Fuzzy Logic Toolbox User’s Guide R2012b. The MathWorks, Inc. 1995–2012.
10. Fuzzy Logic Toolbox User’s Guide R2012b. The MathWorks, Inc. 1995–2012.
References
1. Utkin V.I. First Stage of VSS: people and events. Lecture Notes in Control and Information Science. London, UK,
Springer-Verlag Publ., 2002, vol. 274, pp. 1–33.
2. Utkin V.I. Sliding Modes and Their Application in Variable Structure Systems. Moscow, Mir Publ., 1978.
3. Young K.D., Utkin V.I., Ozguner U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst.
Technol. 1999, vol. 7, no. 3, pp. 328–342.
4. Slotine J.J., Li W. Applied Nonlinear Control. Englewood Cliffs, NJ, Prentice-Hall Publ., 1991.
5. Bondarev A.G., Bondarev S.A., Kostylyeva N.Y., Utkin V.I. Sliding modes in systems with asymptotic state observ-ers. Automatica i telemekhanika [Autom. Remote Control]. 1985, vol. 46, no. 5, pp. 679–684.
6. Bartolini G., Fridman L., Pisano A. Modern Sliding Mode Control Theory. Springer Verlag Publ., 2008.
7. Li T.H.S., Shien M. Switching-type fuzzy sliding mode control of a cart-pole system. Mechatronics. 2000, vol. 10,
pp. 91–109.
8. Litvintseva L.V., Ulyanov S.V., Ulyanov S.S. Design of Robust Knowledge Bases of Fuzzy Controllers for Intelligent
Control of Substantially Nonlinear Dynamic Systems: II. A Soft Computing Optimizer and Robustness of Intelligent Control
Systems. Izvestia Rossiyskoy Akademii Nauk. Teoriya i Systemy Upravleniya [Journal of Computer and Systems Sciences In-ternational]. 2006, vol. 45, no. 5, pp. 744–771.
9. Jang J.S. Neuro-Fuzzy and Soft Computing. NJ, USA, Prentice Hall Publ., 1997, pp. 335–368.
10. Fuzzy Logic Toolbox User’s Guide R2012b. The MathWorks, Inc. 1995–2012.



 ) как входные лингвистические переменные нечеткого правила (см. табл.).
) как входные лингвистические переменные нечеткого правила (см. табл.).


 , где w – положительная переменная, определяющая скорость сходимости для e и
, где w – положительная переменная, определяющая скорость сходимости для e и 
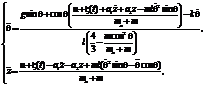 (1)
(1)

 ]=[10 0,1](grad); [z0
]=[10 0,1](grad); [z0 ]=[00].
]=[00]. ]=[00]. Весовой параметр w=5,9.
]=[00]. Весовой параметр w=5,9. езультаты моделирования показали, что только интеллектуальный регулятор, спроектированный с помощью ОБЗ, является робастным. Именно он выполнил поставленную задачу управления.
езультаты моделирования показали, что только интеллектуальный регулятор, спроектированный с помощью ОБЗ, является робастным. Именно он выполнил поставленную задачу управления.