Высокотемпературная микроэлектроника – новое научное направление, которое объединяет передовые физико-технологические и конструктивно-схемотехнические принципы организации нового класса электронных устройств, предназначенных для специальных приложений, где условия эксплуатации отличаются от нормальных. Одними из таких устройств являются микросхемы на структурах кремний на изоляторе (КНИ) – идеальные высокотемпературные устройства, широко применяемые в Вооруженных силах, нефтегазовой, ядерной и других отраслях, где необходимо функционирование в высокотемпературной среде [1].
Значимыми представителями элементной базы КНИ микросхем являются двухзатворные КНИ КМОП-транзисторы [2–4]. Они, как известно, обладают практически значимыми возможностями масштабирования параметров в наноразмерной области [5]. Однако проведение макетных исследований наноэлектронных устройств в высокотемпературной области – очень дорогостоящая опция. Следовательно, возникает необходимость разработки высокотемпературных моделей и методов схемотехнического моделирования для прогнозирования, руководствуясь которыми, можно проектировать электронные устройства [6].
Важным условием развития методов моделиро- вания КНИ КМОП-транзисторов является учет современных требований технологии их изготовления. На современном этапе реальные КНИ КМОП-транзисторы характеризуются наличием вер- тикального гауссового профиля распределения легирующей примеси в рабочей области из-за требования ряда операций имплантации и диффузии во время процесса изготовления [4, 6]. Таким образом, моделирование основных характеристик транзистора, в частности, распределение потенциала в рабочей области, c учетом гауссова профиля легирования может обеспечить более адекватные физические характеристики реальных КМОП-транзисторов [7–9]. К тому же искусственно созданный гауссовый профиль легирующей примеси, как известно, компенсирует проявление нежелательных короткоканальных эффектов в транзисторе, что положительным образом отражается на всех его характеристиках, что определяет актуальность и востребованность такого направления развития моделей и методов моделирования.
Цель данной работы заключается в разработке температурной аналитической модели распределения потенциала неравномерно легированного двухзатворного КНИ КМОП-нанотранзистора. Модель базируется на аналитическом решении 2D-уравнения Пуассона с соответствующими граничными условиями для случая постоянной температуры тела транзистора [10]. Для проверки адекват- ности предложенной модели результаты моделирования сопоставляются с данными, полученными при помощи программного пакета ATLASTM [11] для диапазона температур 200–500 К.
Постановка обобщенной задачи
 Для случая стационарной температуры в рамках концепции зарядового разделения рассмотрим квазиклассическую задачу определения 2D-распределения потенциала в тонкопленочной двухзатворной неравномерно легированной КНИ-транзис- торной структуре. Данная структура схематично представлена на рисунке 1.
Для случая стационарной температуры в рамках концепции зарядового разделения рассмотрим квазиклассическую задачу определения 2D-распределения потенциала в тонкопленочной двухзатворной неравномерно легированной КНИ-транзис- торной структуре. Данная структура схематично представлена на рисунке 1.
В данном случае необходимо решать самосогласованную задачу нахождения распределения 2D-потенциала в рабочей области j(x, y, T), которая связана уравнением Пуассона, записанным в виде:
 , (1)
, (1)
где q – заряд электрона; j(x, y, T) – температурная зависимость распределения потенциала в рабочей области транзистора; eS(T) – температурная зависимость диэлектрической проницаемости материала рабочей области; NA(x, T) – температурная зависимость концентрации легирования рабочей области.
Тепловые процессы в кремниевых транзисторных устройствах можно с некой долей условности разделить на быстрые и медленные. Быстрые процессы оказывают влияние на полупроводниковые свойства тела транзистора (например, ширина запрещенной зоны, собственная концентрация носителей [12]), быстрый отклик, высокий температурный градиент, широкий диапазон воздействия, сравнительно узкий температурный диапазон, вне которого полупроводниковые свойства материала практически исчезают. Медленные процессы связаны с фундаментальными физическими законами. В рассматриваемом случае (1) учитываются температурная зависимость диэлектрической проницаемости кремния и его окисла и процесс термодиффузии примеси в рабочей области транзистора. Данные механизмы характерны для области сверхвысоких температур выше 500 К. Однако при таких высоких температурах даже при принятии специальных мер кремневые устройства перестают функционировать [6]. Поэтому в данной работе рассматривается диапазон температур 200–500 К, который представляет практический интерес.
В рамках указанных приближений правая часть уравнения (1) запишется в виде функции Гаусса:  , где Npick – максимальная концентрация легирующей примеси; Rd – положение пиковой концентрации легирования; sd – крутизна профиля легирующей примеси. А граничные условия для него можно записать так:
, где Npick – максимальная концентрация легирующей примеси; Rd – положение пиковой концентрации легирования; sd – крутизна профиля легирующей примеси. А граничные условия для него можно записать так:
 ;
;
 ;
;
 ;
;
 ;
;
 ,
,
где jf(y, T) – поверхностный потенциал; eox – диэлектрическая проницаемость подзатворного окисла; tf и tb – толщина подзатворного окисла фронтального и обратного затворов соответственно; Ugf и Ugb – напряжение на фронтальном и обратном затворах соответственно; UFB(T) – температурная зависимость напряжения плоских зон; Ubi(T) – температурная зависимость контактной разности потенциалов; Lg, tS – длина и толщина рабочей области транзистора соответственно; Uds – напряжение сток-исток.
Известно, что напряжение плоских зон для фронтального и обратного затворов
 ,
,
где ФMS – работа выхода; cf – сродство электрона; Eg(T) – ширина запрещенной зоны; UF(T) – уровень Ферми. Температурная зависимость ширины запрещенной зоны  , где Eg(0) – ширина запрещенной зоны при 0 К;
, где Eg(0) – ширина запрещенной зоны при 0 К;  – температурный градиент ширины запрещенной зоны; T0 – начальная температура (оба последних параметра являются по сути подгоночными и определяются экспериментально). Температурная зави- симость уровня Ферми
– температурный градиент ширины запрещенной зоны; T0 – начальная температура (оба последних параметра являются по сути подгоночными и определяются экспериментально). Температурная зави- симость уровня Ферми  , где
, где  – тепловой потенциал; k – константа Больцмана;
– тепловой потенциал; k – константа Больцмана;
 – собственная концентрация носителей; Nc(300) и Nv(300) – плотность поверхностных состояний в зоне проводимости и валентной зоне при температуре 300 К соответственно;
– собственная концентрация носителей; Nc(300) и Nv(300) – плотность поверхностных состояний в зоне проводимости и валентной зоне при температуре 300 К соответственно;
 – контактная разность потенциалов; Uds – напряжение сток-исток; Nds – максимальная концентрация легирования областей стока и истока.
– контактная разность потенциалов; Uds – напряжение сток-исток; Nds – максимальная концентрация легирования областей стока и истока.
Свойства гауссова профиля легирования
 На рисунке 2 приведены характерные распределения профиля легирования (функция Гаусса) по глубине рабочей области (в ортогональной плоскости) при ее фиксированной толщине.
На рисунке 2 приведены характерные распределения профиля легирования (функция Гаусса) по глубине рабочей области (в ортогональной плоскости) при ее фиксированной толщине.
Следует отметить, что уровень приповерхностной концентрация легирования (например NA(0)) существенно зависит от величины параметра sd. В области малых значений sd приповерхностная концентрация может отличаться от максимальной более чем на порядок. При этом протяженность этих областей (у верхнего и нижнего затворов) вдоль оси х (по глубине рабочей области) является конечной. Например, при sd = 1 нм протяженность этих областей составляет примерно 1,9 нм, а приповерхностная концентрация отличается на три порядка от максимальной. Следует отметить, что при уменьшении толщины tS спад параметра NA(0) за- медляется. Для получения тех же концентраций необходимо уменьшать sd пропорционально отно- шению толщин. В области больших значений sd отношение NA(0) / Npuck ® 1. Поэтому с некоторого значения tS можно считать рабочую область равномерно легированной.
Распределение потенциала
В рабочей области рассматриваемой структуры 2D-уравнение Пуассона при переходе к новой координате при помощи новой переменной  и с учетом вышеизложенных допущений имеет следующий вид:
и с учетом вышеизложенных допущений имеет следующий вид:
 (2)
(2)
Аналитическое решение уравнения (2) аппроксимируется полиномом с коэффициентами в виде функций, зависящих от y:
 , (3)
, (3)
где вспомогательная функция g(r) представлена в виде  ; специальная функция
; специальная функция  – интеграл вероятности, является, как известно, одной из наиболее используемых в теории и практике специальных функций [13].
– интеграл вероятности, является, как известно, одной из наиболее используемых в теории и практике специальных функций [13].
При таком выборе решения уравнения (1) функции am(y, T) (m = 0, 1, 2) определяются исходя из граничных условий, в которых учитываются температурные зависимости:
 ;
;

 (4)
(4)
 ;
;
 ,
,
где jb(y, T) – распределение потенциала вдоль обратной поверхности;  и
и 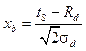 – новые координаты фронтальной и обратной поверхностей соответственно;
– новые координаты фронтальной и обратной поверхностей соответственно;  .
.
Выражение для функций a1(y), a2(y), a2(y), входящих в (3), можно записать в виде



где gb = g(xb), gf = g(xf),  – коэффициент нормировки функций am(y, T).
– коэффициент нормировки функций am(y, T).
После несложных, но громоздких вычислений заключительное выражение для 2D-потенциала j(r, y, T) можно представить в виде
 (5)
(5)
где aj – коэффициент нормировки потенциала и xm – вспомогательные функции. Их выражения приведены в [10]. Связь поля Eb с напряжением на обратном затворе Ugb можно, например, представить так [4]:
 .
.
Выражение для температурной зависимости фронтального поверхностного потенциала jf(y, T) можно записать в виде
 (6)
(6)
где B1(T) и B2(T) – произвольные коэффициенты;  – характеристическая длина для фронтальной поверхности;
– характеристическая длина для фронтальной поверхности;  – масштабирующий коэффициент потенциала на фронтальной поверх- ности,
– масштабирующий коэффициент потенциала на фронтальной поверх- ности,  ,
, 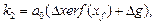 Dg = gb – gf.
Dg = gb – gf.
Выражения для температурной зависимости jb(y, T) можно записать в виде
 (7)
(7)
где B3(T) и B4(T) – произвольные коэффициенты;  – характеристическая длина для обратной поверхности;
– характеристическая длина для обратной поверхности;  – масштабирующий коэффициент потенциала на обратной поверхности.
– масштабирующий коэффициент потенциала на обратной поверхности.
Используя граничные условия (4), можно получить выражения для функций Bm(T):
 ;
;
 ; (8)
; (8)
 ;
;
 ,
,
где выражения для функций ui(T) и ri приведены в [10]. Необходимо только соотношения  и
и  заменить на следующие:
заменить на следующие:


Температурные зависимости основных физических величин
Температурная зависимость распределения потенциала в основном определяется температурными зависимостями таких физических величин, как ширина запрещенной зоны, собственная концентрация, встроенная разность потенциалов и напряжение плоских зон [12].
 Температурная зависимость ширины запрещенной зоны для КНИ структуры показана на рисунке 3.
Температурная зависимость ширины запрещенной зоны для КНИ структуры показана на рисунке 3.
Такой вид близкой к линейной зависимости в исследуемом диапазоне температур обусловливается температурным изменением взаимодействия носителей с решеткой и температурной зависимо- стью распределения фононов вследствие линейных колебаний решетки [10].
Температурная зависимость собственной концентрации, приведенная на рисунке 1, имеет выраженный нелинейный характер. Следует отметить, что с ростом температуры величина собственной концентрации резко возрастает. Она каждый раз удваивается при повышении температуры примерно на 10 К. Поэтому при высоких температурах процесс термогенерации становится определяющим для концентрации носителей [12].
Положение уровня Ферми определяется уровнем собственной концентрации носителей. Поскольку при повышении температуры уровень собственной концентрации растет быстрее, чем тепловой потенциал, уровень Ферми будет приближаться к нижней границе запрещенной зоны, что иллюстрируется результатами расчетов, приведенными на рисунке 4. Аналогичным поведением характеризуется и контактная разность потенциалов, показанная на рисунке 4.

Важно отметить, что характер поведения темпе- ратурных зависимостей основных физических величин анализируемых структур одинаков.
Результаты моделирования распределения потенциала
Для модельных расчетов был выбран прототип двухзатворного КНИ КМОП-нанотранзистора n-типа с гауссовым вертикальным профилем ле- гирования. Параметры устройства, отвечающие современным требованиям, таковы: Lg = 45 нм, tS = = 10 нм, tf = 1,8 нм, tb = 50 нм, Npick = 1 ´ 1016 см-3. На рисунке 5 приведены численно рассчитанные распределения фронтального поверхностного потенциала вдоль рабочей области при разных значениях sd при фиксированных напряжениях на контактах транзистора.

При помощи соотношений (6–8) для малосигнального случая Uds = Ugf = 0.1 В и Ugb = 0 В вычислены значения фронтального поверхностного потенциала для разных значений температур. На рисунке 6 показано распределение данного потенциала для значений крутизны профиля легирования 3 и 10 нм в диапазоне температур от 200 до 500 К.

Такой вид распределения фронтального потенциала обусловлен температурной зависимостью физических величин, рассмотренных выше. В результате абсолютное значение фронтального поверхностного потенциала снижается с повышением температуры. Однако его нормированная величина возрастает с ростом температуры во всех точках канала [14]. Это связано с тем, что с повышением температуры увеличивается собственная концентрация носителей, а уровень Ферми понижается. Из результатов моделирования следует, что в исследуемом диапазоне температур зависимость величины изменения потенциала от температуры в любой точке канала носит нелинейный характер.
Этот вывод касается и поведения температурной зависимости минимума поверхностного потенциала jf min. Функция jf min, как известно, используется для моделирования ключевых характеристик КНИ-нанотранзисторов [15]. Полезным результатом для практических приложений является также температурный градиент минимума поверхностного потенциала для разных значений крутизны профиля легирования. Результаты расчетов для исследуемого прототипа отражены на рисунке 7.

Из представленных данных следует, что изменение температурных свойств транзисторной структуры зависит от sd. При небольших значениях sd температурный градиент grad(jf min) практически постоянен во всем исследуемом диапазоне температур, что и определяет линейный характер зависимости jf min и остальных ключевых параметров транзистора, связанных с jf min. Для больших sd температурный градиент нелинейный. В данном случае это проявляется начиная с температуры примерно 350 К. Поэтому в области высоких тем- ператур будет проявляться существенная дегра- дация зависимости jf min и остальных ключевых параметров транзистора, связанных с ним. Для ни- велирования этого эффекта и повышения верхней границы температурного диапазона на 100 К необходимо увеличивать уровень легирования рабочей области на порядок.
Заключение
Разработана 2D-аналитическая температурная модель распределения потенциала в рабочей области двухзатворного тонкопленочного полевого нанотранзистора со структурой кремний на изоляторе с неоднородно легированной рабочей областью в виде функции Гаусса. Модель построена на основе аналитического решения 2D-уравнения Пуассона, полученного в параболическом приближении о виде распределения потенциала, с использованием специальной функции – интеграл ошибок.
В диапазоне температур 200–500 К численно исследованы температурные зависимости распределения основных физических характеристик транзисторной структуры и поверхностного потенциала от крутизны профиля легирования. Результаты моделирования находятся в хорошем соответствии с данными моделирования, полученными при помощи коммерчески доступного программного пакета ATLASTM, предназначенного для 2D-моделирования транзисторных структур.
Работа выполнена при поддержке Программы фундаментальных исследований РАН № 43.35 НИР № 0065-2018-0006.
Литература
1. Colinge J.P. Multiple-gate SOI MOSFETs. Solid-State Electronics, 2004, vol. 48, no. 3, pp. 897–909.
2. Kranti A., Armstrong G.A. Engineering source/drain exten- sion regions in nanoscale double gate (DG) SOI MOSFETs: Analyt- ical model and design considerations. Solid-State Electronics, 2006, vol. 50, no. 2, pp. 437–447.
3. Nikolic B. Design in the power-limited scaling regime. IEEE Trans. Electron Devices, 2008, vol. 55, no. 1, pp. 71–83.
4. Suzuki K., Yuji K., Susumu N., Charles W.M., Temel H.B., Tsutomu N. Analytical model for redistribution profile of ion-implanted impurities during solid-phase epitaxy. IEEE Trans. Electron Devices, 2007, vol. 54, no. 2, pp. 262–271.
5. Масальский Н.В. Характеристики двухзатворных КНИ КМОП-нанотранзисторов для перспективных технологий с низким уровнем потребляемой мощности // Микроэлектроника. 2012. Т. 41. № 6. С. 436–444.
6. International technology roadmap for semiconductor 2015. URL: http://public.itrs.net/ (дата обращения: 17.03.2018).
7. Reyboz M., Rozeau O., Poiroux T., Martin P., Jomaah J. An explicit analytical charge based model of undoped independent Double-Gate MOSFET. Solid-State Electronics, 2006, vol. 50, no. 8, pp. 1276–1285.
8. Moldovan O., Cerdeira A., Jiménez D., Raskin J.-P., Kilchytska V., Flandre D., Collaert N., Iñiguez B. Compact model for highly-doped double-gate SOI MOSFETs targeting baseband analog applications. Solid-State Electronics, 2007, vol. 51, no. 5, pp. 655–661.
9. Cerdeira A., Iñiguez B., Estrada M. Compact model for short channel symmetric doped double-gate MOSFETs. Solid-State Electronics, 2008, vol. 52, no. 4, pp. 1064–1070.
10. Масальский Н.В. Моделирование распределения потенциала в неоднородно легированной рабочей области двухзатворного КНИ КМОП-нанотранзистора // Микроэлектроника. 2017. Т. 46. № 2. С. 151–160.
11. Silvaco Int. 2004: ATLAS User’s Manual A 2D numerical device simulator. URL: https://www.silvaco.com/products/tcad/ device_simulation/atlas/atlas.html (дата обращения: 21.03.2018).
12. Зи С. Физика полупроводниковых приборов: В 2 кн. М.: Мир, 1984. Кн. 1. 456 с.
13. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Физматгиз, 1978. 720 с.
14. Han J.W., Kim C.J., Choi Y.K. Universal potential model in tied and separated double-gate MOSFETs with consideration of symmetric and separated asymmetric structure. IEEE Trans. Electron Devices, 2008, vol. 55, no. 5, pp. 1472–1480.
15. Масальский Н.В. Проблемы схемотехнического моделирования нанотранзисторов со структурой кремний на изоляторе // Программные продукты и системы. 2013. № 4. С. 60–67.
References
- Colinge J.P. Multiple-gate SOI MOSFETs. Solid-State Electronics. 2004, vol. 48, no. 3, pp. 897–909.
- Kranti A., Armstrong G.A. Engineering source/drain extension regions in nanoscale double gate (DG) SOI MOSFETs: Analytical model and design considerations. Solid-State Electronics. 2006, vol. 50, no. 2, pp. 437–447.
- Nikolic B. Design in the power-limited scaling regime. IEEE Trans. Electron Devices. 2008, vol. 55, no. 1, pp. 71–83.
- Suzuki K., Yuji K., Susumu N., Charles W.M., Temel H.B., Tsutomu N. Analytical model for redistribution profile of ion-implanted impurities during solid-phase epitaxy. IEEE Trans. Electron Devices. 2007, vol. 54, no. 2, pp. 262–271.
- Masalsky N.V. Characteristics of double gate SOI CMOS nanotransistors for perspective technologies with the low supply power. Microelectronics. 2012, vol. 41, no. 6, pp. 436–444 (in Russ.).
- International technology roadmap for semiconductor. Available at: http://public.itrs.net/ (accessed March 17, 2018).
- Reyboz M., Rozeau O., Poiroux T., Martin P., Jomaah J. An explicit analytical charge based model of undoped independent Double-Gate MOSFET. Solid-State Electronics. 2006, vol. 50, no. 8, pp. 1276–1285.
- Moldovan O., Cerdeira A., Jiménez D., Raskin J.-P., Kilchytska V., Flandre D., Collaert N., Iñiguez B. Compact model for highly-doped double-gate SOI MOSFETs targeting baseband analog applications. Solid-State Electronics. 2007, vol. 51, no. 5, pp. 655–661.
- Cerdeira A., Iñiguez B., Estrada M. Compact model for short channel symmetric doped double-gate MOSFETs. Solid-State Electronics. 2008, vol. 52, no. 4, pp. 1064–1070.
- Masalsky N.V. Simulation of the potential distribution in an inhomogeneously doped workspace of a double-gate SOI CMOS nanotransistor. Russian Microelectronics, 2017, vol. 46, no. 2, pp. 139–148 (in Russ.).
- ATLAS User’s Manual A 2D Numerical Device Simulator. Available at: https://www.silvaco.com/products/tcad/device_simulation/atlas/atlas.html Silvaco Int. 2004 (accessed March 21, 2018).
- Sze S.M. Physics of Semiconductor Devices. Wiley-Interscience Publ. NY, Chichester, Brisbane, Toronto, Singapore, 1981.
- Korn G., Korn Т. Mathematical Handbook for Scientists and Engineers. McGraw-Hill Book Comp., NY, Sun Francisco, Toronto, London, Sidney, 1981.
- Han J.W., Kim C.J., Choi Y.K. Universal potential model in tied and separated double-gate MOSFETs with consideration of symmetric and separated asymmetric structure. IEEE Trans. Electron Devices. 2008, vol. 55, no. 5, pp. 1472–1480.
- Masalsky N.V. Nanotransitors circuitry simulation problems with silicon-on-insulator structure. Software & Systems, 2013, no. 3,
pp. 60–67 (in Russ.).




 , (1)
, (1) , где Npick – максимальная концентрация легирующей примеси; Rd – положение пиковой концентрации легирования; sd – крутизна профиля легирующей примеси. А граничные условия для него можно записать так:
, где Npick – максимальная концентрация легирующей примеси; Rd – положение пиковой концентрации легирования; sd – крутизна профиля легирующей примеси. А граничные условия для него можно записать так: ;
; ;
; ;
; ;
; ,
, ,
, , где Eg(0) – ширина запрещенной зоны при 0 К;
, где Eg(0) – ширина запрещенной зоны при 0 К;  – температурный градиент ширины запрещенной зоны; T0 – начальная температура (оба последних параметра являются по сути подгоночными и определяются экспериментально). Температурная зави- симость уровня Ферми
– температурный градиент ширины запрещенной зоны; T0 – начальная температура (оба последних параметра являются по сути подгоночными и определяются экспериментально). Температурная зави- симость уровня Ферми  , где
, где  – тепловой потенциал; k – константа Больцмана;
– тепловой потенциал; k – константа Больцмана; – собственная концентрация носителей; Nc(300) и Nv(300) – плотность поверхностных состояний в зоне проводимости и валентной зоне при температуре 300 К соответственно;
– собственная концентрация носителей; Nc(300) и Nv(300) – плотность поверхностных состояний в зоне проводимости и валентной зоне при температуре 300 К соответственно; – контактная разность потенциалов; Uds – напряжение сток-исток; Nds – максимальная концентрация легирования областей стока и истока.
– контактная разность потенциалов; Uds – напряжение сток-исток; Nds – максимальная концентрация легирования областей стока и истока.
 и с учетом вышеизложенных допущений имеет следующий вид:
и с учетом вышеизложенных допущений имеет следующий вид: (2)
(2) , (3)
, (3) ; специальная функция
; специальная функция  – интеграл вероятности, является, как известно, одной из наиболее используемых в теории и практике специальных функций [13].
– интеграл вероятности, является, как известно, одной из наиболее используемых в теории и практике специальных функций [13]. ;
;
 (4)
(4) ;
; ,
, и
и 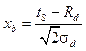 – новые координаты фронтальной и обратной поверхностей соответственно;
– новые координаты фронтальной и обратной поверхностей соответственно;  .
.


 – коэффициент нормировки функций am(y, T).
– коэффициент нормировки функций am(y, T). (5)
(5) .
. (6)
(6) – характеристическая длина для фронтальной поверхности;
– характеристическая длина для фронтальной поверхности;  – масштабирующий коэффициент потенциала на фронтальной поверх- ности,
– масштабирующий коэффициент потенциала на фронтальной поверх- ности,  ,
, 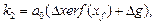 Dg = gb – gf.
Dg = gb – gf. (7)
(7) – характеристическая длина для обратной поверхности;
– характеристическая длина для обратной поверхности;  – масштабирующий коэффициент потенциала на обратной поверхности.
– масштабирующий коэффициент потенциала на обратной поверхности. ;
; ; (8)
; (8) ;
; ,
, и
и  заменить на следующие:
заменить на следующие:






