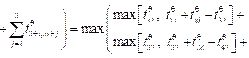Синхронный режим распределенных вычислений при непрерывном выполнении блоков ограниченного числа копий программного ресурса
| Павлов П.А. (pavlov.p@polessu.by) - Полесский государственный университет, Беларусь, г. Пинск (доцент), Пинск, Беларусь, кандидат физико-математических наук, Коваленко Н.С. (kovalenkons@rambler.ru) - Белорусский государственный экономический университет, г. Минск (профессор), Минск, Беларусь, доктор физико-математических наук | |
| Ключевые слова: синхронный режим, распределенные вычисления, структурирование, конвейеризация, программный ресурс, диаграмма Ганта, функционал Беллмана–Джонсона |
|
| Keywords: synchronous mode, distributed computing, the structurization, pipelining, the program resource, Gantt diagram, Bellman-Johnson functional |
|
|
|
|
Введение. Распределенные вычисления – перспективная и динамично развивающаяся область организации параллелизма [1–3]. Данный термин обычно используется при параллельной обработке данных на множестве обрабатывающих устройств, удаленных друг от друга, в которых передача данных по линиям связи приводит к существенным временным задержкам. Перечисленные условия характерны, например, при организации вычислений в многомашинных вычислительных комплексах, вычислительных кластерах, многопроцессорных системах, локальных или глобальных сетях. Создание высокопроизводительных мно- гопроцессорных систем и вычислительных комплексов характеризуется широким проникновением в аппаратное и программное обеспечение фундаментальных принципов распараллеливания и конвейеризации вычислений. В связи с этим происходит пересмотр математических методов и алгоритмов решения задач в различных предметных областях вплоть до всего алгоритмического багажа прикладной математики, выдвигаются новые требования к построению и исследованию математических моделей, касающихся различных аспектов параллельной и конвейерной организации вычислений [4]. Необходимость и актуальность исследований в этих направлениях связана также с тем, что принципы структурирования, распараллеливания и конвейеризации носят достаточно общий характер и присущи процессам различной природы [5, 6]. Случай, когда в общей памяти многопроцессорных систем имеется одна копия программного ресурса, был изучен в работах [7–9] с различных точек зрения. Но, к сожалению, не найдено работ по математическому моделированию функционирования распределенных систем, в которых в общей памяти не одна, а несколько копий программного ресурса. Поэтому изучение задач, относящихся к оптимальной организации распределенных параллельных вычислений, приобретает особую актуальность, когда в общей памяти многопроцессорных систем может одновременно размещаться ограниченное число копий программного ресурса. Такое обобщение носит принципиальный характер ввиду того, что отражает основные черты мультиконвейерной обработки, а также позволяет сравнить эффективность конвейерной и параллельной обработки. Математическая модель распределенных вычислений Конструктивными элементами для построения математических моделей, реализующих методы распределенных вычислений, являются понятия процесса и программного ресурса. Будем рассматривать процесс как последовательность наборов команд (процедур, блоков, подпрограмм) Is = (1, 2, …, s). Процессы, влияющие на поведение друг друга путем обмена информацией, называют кооперативными или взаимодействующими. Многократно выполняемую в многопроцессорной системе программу или ее часть будем называть программным ресурсом, а множество соответствующих процессов – конкурирующими. Математическая модель системы распределенной обработки конкурирующих взаимодействующих процессов при ограниченном числе копий программного ресурса включает в себя – p ³ 2 процессоров многопроцессорной системы, имеющих доступ к общей памяти; – n ³ 2 распределенных конкурирующих процессов; – s ³ 2 блоков структурированного на блоки программного ресурса; – матрицу – 2 £ c £ p копий структурированного на блоки программного ресурса, которые могут одновременно находиться в оперативной памяти, доступной для всех p процессоров; – q > 0 – параметр, характеризующий время дополнительных системных расходов, связанных с организацией конвейерного режима использования блоков структурированного программного ресурса множеством взаимодействующих конкурирующих процессов при распределенной обработке. Предположим, что число блоков програм- много ресурса 1) ни один из процессоров не может обрабатывать одновременно более одного блока; 2) процессы выполняются в параллельно-конвейерном режиме группами, то есть осуществляется одновременное (параллельное) выполнение c копий каждого блока в сочетании с конвейеризацией группы из c копий Qj-го блока по процессам и процессорам, где 3) обработка каждого блока программного ресурса осуществляется без прерываний; 4) распределение блоков Qj, Время выполнения неоднородных процессов при достаточном числе процессоров В рамках математической модели распределенных вычислений при ограниченном числе копий программного ресурса исследуем первый синхронный режим взаимодействия процессов, процессоров и блоков, который обеспечивает непрерывное выполнение блоков структурированного программного ресурса внутри каждого процесса, то есть все процессы являются активными. В этом режиме в случае, когда Система n распределенных конкурирующих процессов называется неоднородной, если времена выполнения блоков программного ресурса Q1, Q2, …, Qs зависят от объемов обрабатываемых данных и/или их структуры, то есть разные для разных процессов. Рассмотрим случай, когда число процессоров распределенной неоднородной многопроцессорной системы является достаточным, то есть Обозначим через
Для вычисления времени выполнения
Здесь Найдем
Следовательно, время выполнения Время реализации неоднородных процессов в условиях ограниченного параллелизма Рассмотрим общий случай, то есть когда
На рисунке 2 изображена диаграмма Ганта для многопроцессорных систем с парамет- рами p = 7, n = 4, s = 6, c = 2,
Для дальнейшего исследования, как и при достаточном числе процессоров, все множество процессов разобьем на подмножества, причем каждое из них будет состоять из m процессов с номерами ▪ ▪ ▪
▪ Найдем значения
Если j = 1, q = 1, i = 1, имеем
Если j = 1, q = 1, i = 2, имеем
Если
Если
Если Если Если Если Из анализа диаграмм Ганта (рис. 2) видно, что минимальное общее время выполнения неоднородных распределенных процессов, конкурирующих за использование c копий структурированного программного ресурса в случае
где Здесь
Значение
Для многопроцессорных систем (рис. 2) получим
В случае, когда
где Значения ▪ ▪ ▪ Здесь
Если
Если
Если
Если
Следовательно, Тогда время выполнения n = 4 неоднородных распределенных конкурирующих процессов, использующих c = 2 копии структурированного на s = 8 блоков программного ресурса в многопроцессорной системе с p = 7 процессо- рами с учетом дополнительных системных расходов q, будет определяться по формуле
Заключение Полученные результаты можно использовать, например, при исследовании асинхронного и второго синхронного режимов взаимодействия процессов, процессоров и блоков структурированного программного ресурса, при сравнительном анализе различных режимов распределенных вычислений, при математическом исследовании эффективности и оптимальности мультиконвейерной организации вычислений, при решении задач построения оптимальной компоновки блоков программного ресурса и нахождения оптимального числа процессоров, обеспечивающих директивное время выполнения заданных объемов вычислений. Список литературы 1. Антонов А.С., Афанасьев И.В., Воеводин Вл.В. Высокопроизводительные вычислительные платформы: текущий статус и тенденция развития // Вычислительные методы и программирование. 2021. Т. 22. С. 135–177. doi: 10.26089/NumMet.v22r210. 2. Бурдонов И.Б., Евтушенко Н.В., Косачев А.С. Реализация распределенных и параллельных вычислений в сети SDN // Тр. ИСП РАН. 2022. Т. 34. С. 159–172. doi: 10.15514/ISPRAS-2022-34(3)-11. 3. Роби Р., Замора Дж. Параллельные и высокопроизводительные вычисления; [пер. с англ.]. М.: ДМК Пресс, 2021. 800 с. 4. Топорков В.В., Емельянов Д.М. Модели, методы и алгоритмы планирования в грид и облачных вычислениях // Вестн. МЭИ. 2018. № 6. С. 75–86. doi: 10.24160/1993-6982-2018-6-75-86. 5. Zaiets N., Shtepa V., Pavlov P., Elperin I., Hachkovska M. Development of a resource-process approach to increasing the efficiency of electrical equipment for food production. Eastern-European J. of Enterprise Technologies, 2019, vol. 5/8, no. 101, pp. 59–65. doi: 10.15587/1729-4061.2019.181375. 6. Каплун В.В., Штепа В.Н., Прокопеня О.Н. Ресурсно-процессная модель энергоменеджмента локального объекта с несколькими источниками энергии // Вестн. БрГТУ. Сер. Машиностроение. 2019. № 4. С. 86–91. 7. Pavlov P.А. The optimality of software resources structuring through the pipeline distributed processing of competitive cooperative processes. IJMT, 2012, vol. 2, no. 1, pp. 5–10. 8. Коваленко Н.С., Павлов П.А., Овсец М.И. Задачи оптимизации числа процессоров и построения оптимальной компоновки распределенных систем // Вестн. БГУ. Сер. 1: Физика. Математика. Информатика. 2012. № 1. С. 119–126. 9. Kovalenko N.S., Pavlov P.А., Ovseec M.I. Asynchronous distributed computations with a limited number of copies of a structured program resource. Cybernetics and systems analysis, 2012, vol. 48, no. 1, pp. 86–98. doi: 10.1007/s10559-012-9385-z. 10. Лазарев А.А. Теория расписаний. Методы и алгоритмы. М., 2019. 408 с. References
|
http://swsys.ru/index.php?id=5054&lang=.docs&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Распределенные вычисления при ограниченном числе копий программного ресурса
- Оптимальность структурирования программных ресурсов при конвейерной распределенной обработке
- Повышение вычислительной мощности персонального компьютера за счет интеграции с распределенной системой из смартфонов
- Анализ процесса распараллеливания программы
- Основы построения тренажерно-обучающих систем сложных технических комплексов


 .
.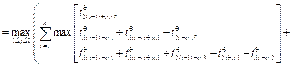



 ,
, 


 – общее время выполнения f-й группы блоков всеми n процессами на
– общее время выполнения f-й группы блоков всеми n процессами на 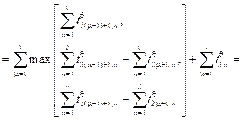
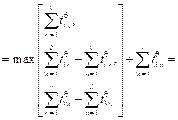




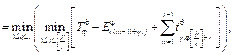






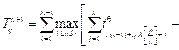

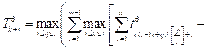









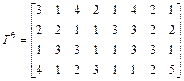 построены не- совмещенные и совмещенные диаграммы Ганта. Найдем минимальное время выполнения процессов для данной многопроцессорной системы:
построены не- совмещенные и совмещенные диаграммы Ганта. Найдем минимальное время выполнения процессов для данной многопроцессорной системы: