Введение. Модели твердого тела широко используются, в частности, в компьютерных играх, художественных фильмах, в технике, промышленности, военном деле. Динамическое взаимодействие твердых тел применяется в наноструктурированных объектах, где даже небольшое изменение дисперсности или состава компонентов нанокомпозита приводит к существенному изменению макроскопических физико-механических характеристик.

Моделирование динамики множества тел требует точного определения контакта, и из-за небольших временных интервалов необходимы большие вычислительные затраты. Это является фундаментальной задачей во многих областях. Методы моделирования динамиче- ских систем с событиями контактного воздействия являются важным инструментом и популярной стратегией для моделирования твердых тел. В то же время с помощью таких методов приходится решать ряд хорошо известных проблем, включая пересечения, нестабильность, неточности и низкие эксплуатационные характеристики, которые возрастают по мере усложнения контактной задачи. Контактная динамика – это численный метод для вычисления динамического движения совокупности тел, подверженных односторонним ограничениям невзаимопроникновения, с учетом трения  в случае контакта, а также скачков скорости, которые могут возникнуть в результате столкновений.

Одной из значительных проблем при моделировании твердых тел является присущая динамике негладкость [1]. Это происходит, когда твердые тела мгновенно меняют свою скорость при столкновениях с другими поверхностями. Жесткие ограничения на твердое тело, связанные с отсутствием взаимопроникновения и незначительной деформацией, затрудняют определение контакта, который сильно зависит от изменений конфигурации и положения [2, 3].

Основная цель данного исследования – разработка алгоритмов, регулирующих поведение функционально заданных объектов, которые всегда дают реалистичные и выполнимые результаты с максимально возможной скоростью.

Задачи – оценка влияния трения, необходимого для реалистичности физического моделирования, а также разработка быстрого и эффективного симулятора функционально заданных объектов. Геометрический анализ осуществимости импульсов трения важен при построении модели трения.

Новизна работы заключается в способе определения трения, основанного на объединении трения качения и скольжения, а также  в вычислении допустимой скорости и реакции на трение для всех объектов. Предложен простой и эффективный метод реализации ограничений. При моделировании основной упор сделан на физическую точность.

В работе рассмотрен симулятор функционально заданных объектов, который может быть интегрирован с различными системами визуализации, анимации и обнаружения столкновений. Симулятор включает множество слож- ных режимов, таких как перекатывание, скольжение, укладка, переворачивание и распространение ударов, а также соответствующие переходы между ними. Это дает реалистичное поведение для твердого тела, находящегося  в контакте с множеством фиксированных ограничений.

Для настройки с несколькими объектами каждое тело рассматривается как независимая система, в которой все остальные движущиеся тела накладывают аффинные ограничения на уровне скорости. Это эффективно, поскольку включается контактная информация первого порядка для каждого тела. Таким образом, получаются скорости, обеспечивающие непроникающее поведение, по крайней мере, локально на следующем этапе. При этом вводится приблизительное сохранение импульса для многих одновременных контактов, для чего вычисля- ется аффинное ограничение для каждого кон- такта, использующее скорость контакта в момент максимального сжатия. В совокупности это реализуется алгоритмом моделирования множества тел, который является линейным по общему количеству контактов, обрабатываемых для всех объектов на каждом шаге. Внедрено несколько практических оптимизаций  для дальнейшего повышения производительности – так сокращается количество обрабатываемых контактов и для увеличения скорости, и для упрощения внедрения. Также отфильтровываются многие первоначально обнаруженные контакты, игнорируются удовлетворяющие ограничения, то есть контакты, от которых объект удаляется с достаточной скоростью.

Динамика твердого тела находит применение, например, в машиностроении, робототехнике, нанотехнологии, аэрокосмической промышленности, молекулярной динамике. Она позволяет предсказывать и объяснять движение и поведение твердых тел в различных условиях и с разными внешними воздействиями.

В статье [4] рассматривается алгоритм идентификации инерционных параметров и контактных сил, связанных с объектом. Используется известная формулировка взаимодополняемости для разрешения контакта, чтобы установить взаимосвязь замкнутой формы между инерционными параметрами, контактными силами и наблюдаемыми движениями. Взаимодополняемость является полезным средством анализа контактов состояния.

Современные популярные подходы к ре- шению проблемы множественных контактов  с трением зависят от порядка столкновений и применяют решение линейной задачи о дополнительности. В [5] описана аппаратная структура параллельной обработки для решения линейной задачи о дополнительности (LCP).

В статье [6] предлагается новый метод для решения линейной задачи о дополнительности при интерактивном моделировании твердого тела, основанный на методе Гаусса–Зайделя.

Возникающие контактные проблемы можно также решить, используя множители Лагранжа для представления неизвестной величины сил реагирования. В отличие от решения линейной задачи о дополнительности в работе [7] применяется прямое решение задачи смешанной  линейной дополнительности, не требующее  построения матрицы LCP.

Большая часть трудностей при разрешении контактов возникает из-за неопределенности, связанной с установлением того, какие точки контакта действительно активны, то есть способствуют реагированию в данный момент времени. Для проверки, является ли ограничение активным или пассивным, требуется функция расстояния между частями тел. В статье [8] дается строгое определение функции расстояния и выводятся ее некоторые свойства.

В [9] представлен метод обработки фрикционного контакта для жестких и деформируемых объектов. Метод позволяет решить основные трудности, присущие негладкому характеру фрикционного контакта.

В статье [10] описывается конечно-элементная модель при моделировании твердого тела. После определения столкновения между объектами генерируется ответный импульс для распространения на другие объекты, уже находящиеся в контакте со сталкивающимися телами.

В [11] представлен неявный пошаговый алгоритм для динамики твердого тела с контактом и трением, который гарантирует отсутствие пересечений конфигураций на каждом временном шаге. Хотя метод и менее эффективен, чем альтернативные подходы, с его помощью можно надежно обрабатывать широкий спектр сложных сцен.

В обзорной работе [12] рассматриваются основные методы моделирования динамических систем с событиями контактного воздействия. Представлено описание контактной динамики, а также сделан обзор современного состояния основных аспектов, связанных с дисциплиной контактной динамики. Отмечены недостатки существующих методов и перспективы будущих исследований в области контактной механики в динамике множества тел.

К сожалению, нелинейное поведение трения усложняет проблему контакта твердого тела. Традиционно контакт разрешался с использованием сложных схем и методов обна- ружения столкновений с учетом того, что он  происходит между полигонами. Хотя полигональные поверхности являются эффективным средством представления твердых тел, им не хватает некоторых внутренних свойств, важных для разрешения контакта. Как правило, поверхности базы полигонов не снабжены внутренним и внешним разделением или плавным полем расстояний вблизи поверхности.

Авторы данного исследования предлагают новый метод решения проблемы фрикционных контактов с использованием функций возмущения. В работе представлен алгоритм определения скорости для моделирования больших наборов функциональных объектов. При этом в методе отсутствуют повторные попарные сравнения между объектами, что дает линейную сложность по общему числу контактов, вычисленных на каждой итерации.

Описание метода

Функционально заданный объект. Объект описывается с помощью функций возмущения и базовой квадрики [13]:

          (1)

где F¢ (x, y, z) – функционально заданный объект; F(x, y, z) – базовая квадрика; i = 1, …,  N – количество функций возмущения; Ri(x, y, z) – возмущение, при этом

     (2)

где Q(x, y, z) – возмущающая квадрика.

Динамическое взаимодействие функциональных объектов. При отсутствии контактов динамика функционального объекта i в его собственной системе координат определяется как

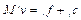,                                        (3)

где iv – поворот функционального объекта i;  if – суммарная сила, состоящая из неконтактных видов, таких как гравитация; M – тензор инерции объекта; ic – слагаемое Кориолиса  (ic = (iv)TM iv).

В случае наличия контакта скорость функционального объекта до обнаружения столкновения составит

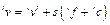,                                 (4)

а скорость после обработки всех контактов –

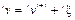,                                          (5)

где s – размер шага; ix – изменение пространственной скорости, вызванное активными контактными ограничениями.

В статье [14] описан алгоритм обнаружения столкновений функционально заданных объектов, где применен менее универсальный, но более быстрый способ определения контакта  из [15].

Анализируется характеристический многочлен, связанный с эллипсоидами и квадриками, для обнаружения контакта. Условие определения столкновения проверяется непосредствен- но по их параметрам. Контакт определяется  с помощью дискриминантов характеристического многочлена. Относительные положения классифицируются по знаку коэффициентов этого многочлена.

Чтобы определить контакты, каждый функциональный объект обрабатывается один раз за шаг, при этом каждый шаг является линейным по общему количеству контактов. Эти границы поддерживаются путем рассмотрения каждого объекта как независимой системы, используя движение других объектов для создания ограничений уровня скорости.

Поскольку другие объекты двигаются, следовательно, накладываются ограничения на перемещение, поэтому добавляется смещение к каждому ограничению контакта на уровне скорости, которое учитывает скорость контактирующего объекта.

Чтобы компенсировать изменение ограничения в течение каждого интервала, каждое ограничение контакта компенсируется относительной скоростью. Каждое ограничение уров- ня скорости будет определять аффинное полупространство.

Для функционального объекта i обозначим пространственную скорость, с которой он имеет общий контакт c, через ivc. Эта скорость преобразуется в систему координат объекта i. Величина скорости контакта вдоль нормали ограничения будет

.                                       (6)

Затем генерируем аффинное ограничение скорости для объекта i, требуя, чтобы его скорость не только была в допустимом направлении, но и имела достаточно большую составляющую вдоль нормали контакта (рис. 1):

.                                    (7)

Каждое такое ограничение, вычисленное по контакту c, определяет допустимое аффинное полупространство.

В общей точке контактас нормалью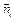задается скорость vc. Скорость объекта i после столкновения должна быть больше, чем mc при проецировании на  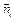(рис. 1).

Сохранение импульса позволяет получить скорость точки контакта вдоль нормали к контакту в момент максимального сжатия. Сначала вычисляется эффективная масса объекта i с инерцией, определяемая силой, действующей вдоль нормали контакта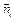, в точке контакта

Пусть vnc – скорость вдоль контактной нормали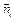, mvnc – соответствующий импульс. Во время максимального сжатия между объектами i и j сохранение импульса подразумевает, что существует скорость вдоль нормали, которая вычисляется следующим образом:

                                (8)

где vnci и vncj – скорости объектов i и j в точке соприкосновения, спроецированные вдоль Данная скорость является средним значением этих двух скоростей, взвешенным по их соответствующим массам.

Модель трения, применяемая в настоящей работе, основана на импульсном методе,  в частности, на алгоритме отслеживания импульсов энергии [16].

Чтобы контакты могли генерировать как нормальные, так и тангенциальные импульсы, запишем следующее уравнение:

,                   (9)

где ix – изменение пространственной скорости, вызванное активными контактными ограничениями; il – встроенный импульс трения, противодействующий скольжению вдоль касательных плоскостей ограничения в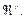

Для окончательных результатов необходимо дополнительно ограничить скользящие повороты, которые будут генерироваться из единичных касательных векторов в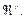

Каждому сгенерированному скользящему повороту определяем обобщенный коэффициент трения yc. Это позволяет создавать характеристики трения, которые могут и быть анизотропными, и изменяться в зависимости от местоположения контакта. Также вычисляем крутящий момент ivt. Нормальный импульс ix  и совокупность фрикционных коэффициентов yc используются для определения импульса трения il.

Алгоритм вычислений. Пошагово выполняем алгоритм вычислений, используя фиксированный размер шага s:

– для каждого функционального объекта предварительно вычисляем базовую поверхность;

– генерируем матрицу инерции с фиксированной диагональю;

– вычисляем положение объекта в мировой системе координат;

– на каждом шаге вычисляем скорости ivi ((4), (5));

– определяем столкновения;

– вычисляем нормали и аффинные расстояния; поскольку вычисляется каждое контактное ограничение, можно немедленно отбросить те, которые строго выполняются (эти ограничения генерируются на ранней стадии конвейера, что позволяет эффективно снизить стоимость каждого шага);

– вычисляем активные контакты для дальнейших вычислений; эти детали отражают встроенную в подход взаимодополняемость на уровне скорости (контактные ограничения, когда удаляется объект, выполняются и поэтому не будут создавать нормальные и тангенциальные импульсы, в то время как все остальные ограничения потенциально активны и поэтому будут создавать импульсы пропорционально степени нарушения их ограничений);

– если контакт обнаружен, для каждого используем нормаль для равномерной выборки конечного набора касательной плоскости  в точке контакта; эти выборки используются для аппроксимации набора всех возможных тангенциальных импульсов при контакте.

Алгоритм вычислений показан на рисунке 2.

Результаты

Производительность метода протестирована на процессоре 12 core 2.5 GHz Intel Xeon E5-2678 v3. Все численные методы реализованы с использованием C++ на CPU, выбран Eigen (https://eigen.tuxfamily.org/index.php?title=Main_Page) в качестве основной библиотеки линейной алгебры, включающей все решения для разреженных линейных систем. Для распараллеливания процессора используется Intel TBB, который позволяет упростить создание и  развертывание многопоточных приложений (https://github.com/oneapi- src/oneTBB). С помощью Intel TBB не надо решать, на какой архи- тектуре и на какой платформе будет использо- ваться программа. Она берет на себя ответственность за работу с потоками.

Результаты тестов сведены в таблицу (для  1 000 эллипсоидов) и проиллюстрированы рисунками 3 и 4.

Каждый шаг реализации разбит на четыре этапа: предварительные вычисления, обнару- жение контакта, разрешение контакта и заключительные вычисления.

Как на предварительном, так и на заключительном этапах каждый объект посещается один раз и выполняется фиксированный объем работы, поэтому сложность для обоих этапов равна O(n2), где n – количество объектов, обрабатываемых симулятором.

Фаза обнаружения контакта отвечает за нахождение всех точек соприкосновения, возникающих между любыми парами объектов при моделировании.

Сложность представленного детектора столкновений с широкой фазой зависит от количества объектов, которые сталкиваются или близки к столкновению: O(n) – наилучший случай, O(n2) – наихудший случай (в физически неправдоподобном случае, когда все n объектов находятся достаточно близко друг к другу).

Из тестов видно, что предлагаемая реализация линейна по количеству моделируемых объектов и по общему количеству точек соприкосновения, обнаруживаемых на каждом шаге.

Была запущена симуляция свободно падающих эллипсоидов в наклонную прозрачную трубу, которые высыпаются из нее на плоскую поверхность.

В таблице показаны статистические данные в ходе моделирования.

Следует отметить продолжающееся увеличение числа контактов после насыщения числа сталкивающихся эллипсоидов в течение времени, когда оседающие объекты собираются вместе.

Также построены графики времени, затраченного на каждый из этапов алгоритма (http://www.swsys.ru/uploaded/image/2024-3/ 6.jpg).

Жесткие ограничения на твердое тело, связанные с отсутствием взаимопроникновения  и незначительной деформацией, затрудняют разрешение контакта и делают его высокочувствительным даже к незначительным изменениям конфигурации и положения.

Заключение

В работе представлен основанный на контакте подход к динамике функциональных объектов, который приводит к непротиворечивой теории и надежному симулятору линейного времени. Подход сформулирован с учетом геометрических параметров, что дает возмож- ность локально обрабатывать множественные контакты с нелинейным трением. Это, в свою очередь, позволяет получить крупномасштабное правдоподобное моделирование функцио- нально заданных объектов с использованием реализованного симулятора.

Список литературы

1.   Wachs A., Uhlmann M., Derksen J., Huet D.P. Modeling of short-range interactions between both spherical and non-spherical rigid particles. In: Modeling approaches and computational methods for particle-laden turbulent flows, 2023, pp. 217–264. doi: 10.1016/B978-0-32-390133-8.00019-0.

2.   Strecke M., Stueckler J. DiffSDFSim: Differentiable rigid-body dynamics with implicit shapes. Proc. Int. Conf. 3DV, 2021, pp. 96–105. doi: 10.1109/3DV53792.2021.00020.

3.   Elandt R., Drumwright E., Sherman M.A., Ruina A. A pressure field model for fast, robust approximation of net contact force and moment between nominally rigid objects. Proc. EEE/RSJ Int. Conf. IROS, 2019, pp. 8238–8245.  doi: 10.1109/IROS40897.2019.8968548.

4.   Fazeli N., Tedrake R., Rodriguez A. Identifiability analysis of planar rigid-body frictional contact. In: Robotics Research. SPAR, 2018, vol. 3, pp. 665–682. doi: 10.1007/978-3-319-60916-4_38.

5.   Kim Y. The Hardware accelerated physics engine with operating parameters controlling the numerical error tole- rance. IJAST, 2018, vol. 119, pp. 145–152. doi: 10.14257/ijast.2018.119.13.

6.   Miyamoto S., Yamashita M. An improved convergence based on accelerated modulus-based Gauss–Seidel method for interactive rigid body simulations. SN Appl. Sci., 2021, vol. 3, art. 266. doi: 10.1007/s42452-021-04238-8.

7.   Verschoor M., Jalba A. Efficient and accurate collision response for elastically deformable models. ACM Tran-sactions on Graphics, 2019, vol. 38, no. 2, art. 17, pp. 1–20. doi: 10.1145/3209887.

8.   Lidstrom P. Kinematics for unilateral constraints in multibody dynamics. MMS, 2017, vol. 22, no. 8, pp. 1654–1687. doi: 10.1177/1081286516642270.

9.   Geilinger M., Hahn D., Zehnder J., Bacher M. ADD: Analytically differentiable dynamics for multi-body systems with frictional contact. ACM Transactions on Graphics, 2020, vol. 39, no. 6, art. 190, pp. 1–15. doi: 10.1145/3414685. 3417766.

10. Coevoet E., Andrews S., Relles D., Kry P.G. Distant collision response in rigid body simulations. Comput. Graphics Forum, 2020, vol. 39, no. 8, pp. 113–122. doi: 10.1111/cgf.14106.

11. Ferguson Z., Li M., Schneider T., Gil-Ureta F. Intersection-free rigid body dynamics. ACM Transactions  on Graphics, 2021, vol. 40, no. 4, art. 183, pp. 1–16. doi: 10.1145/3476576.3476773.

12. Flores P. Contact mechanics for dynamical systems: A comprehensive review. Multibody Syst. Dyn., 2022,  vol. 54, pp. 127–177. doi: 10.1007/s11044-021-09803-y.

13. Вяткин С.И., Долговесов Б.С. Методы интерактивного моделирования и визуализации функционально заданных объектов для 3D-Web приложений // Автометрия. 2022. Т. 58. № 1. С. 111–118. doi: 10.15372/AUT20220112.

14. Вяткин С.И., Долговесов Б.С., Корсун А.С. Определение столкновений функционально заданных объектов с рекурсивным делением объектного пространства // Автометрия. 2003. Т. 39. № 6. С. 119–126.

15. Vazquez M.B., Pereira-Saez M.J., Rodriguez-Raposo A.B., Souto-Salorio M.J. Contact detection between a small ellipsoid and another quadric. Comput. Aided Geometric Design, 2022, vol. 98, art. 102136. doi: 10.1016/j.cagd.2022. 102136.

16. Li Y., Asai M., Chandra B., Isshiki M. Energy-tracking impulse method for particle-discretized rigid-body simulations with frictional contact. Computational Particle Mechanics, 2020, vol. 8, pp. 237–258. doi: 10.1007/s40571-020-00326-5.

References

1. Wachs, A., Uhlmann, M., Derksen, J., Huet, D.P. (2023) ‘Modeling of short-range interactions between both spher-ical and non-spherical rigid particles’, in Modeling Approaches and Computational Methods for Particle-Laden Turbulent Flows, pp. 217–264. doi: 10.1016/B978-0-32-390133-8.00019-0.

2. Strecke, M., Stueckler, J. (2021) ‘DiffSDFSim: Differentiable rigid-body dynamics with implicit shapes’, Proc. Int. Conf. 3DV, pp. 96–105. doi: 10.1109/3DV53792.2021.00020.

3. Elandt, R., Drumwright, E., Sherman, M.A., Ruina, A. (2019) ‘A pressure field model for fast, robust approximation of net contact force and moment between nominally rigid objects’, Proc. EEE/RSJ Int. Conf. IROS, pp. 8238–8245. doi: 10.1109/IROS40897.2019.8968548.

4. Fazeli, N., Tedrake, R., Rodriguez, A. (2018) ‘Identifiability analysis of planar rigid-body frictional contact’, in Robotics Research. SPAR, 3, pp. 665–682. doi: 10.1007/978-3-319-60916-4_38.

5. Kim, Y. (2018) ‘The Hardware accelerated physics engine with operating parameters controlling the numerical error tolerance’, IJAST, 119, pp. 145–152. doi: 10.14257/ijast.2018.119.13.

6. Miyamoto, S., Yamashita, M. (2021) ‘An improved convergence based on accelerated modulus-based Gauss–Seidel method for interactive rigid body simulations’, SN Appl. Sci., 3, art. 266. doi: 10.1007/s42452-021-04238-8.

7. Verschoor, M., Jalba, A. (2019) ‘Efficient and accurate collision response for elastically deformable models’, ACM Transactions on Graphics, 38(2), art. 17, pp. 1–20. doi: 10.1145/3209887.

8. Lidstrom, P. (2017) ‘Kinematics for unilateral constraints in multibody dynamics’, MMS, 22(8), pp. 1654–1687. doi: 10.1177/1081286516642270.

9. Geilinger, M., Hahn, D., Zehnder, J., Bacher, M. (2020) ‘ADD: Analytically differentiable dynamics for multi-body systems with frictional contact’, ACM Transactions on Graphics, 39(6), art. 190, pp. 1–15. doi: 10.1145/ 3414685.3417766.

10. Coevoet, E., Andrews, S., Relles, D., Kry, P.G. (2020) ‘Distant collision response in rigid body simulations’, Comput. Graphics Forum, 39(8), pp. 113–122. doi: 10.1111/cgf.14106.

11. Ferguson, Z., Li, M., Schneider, T., Gil-Ureta, F. (2021) ‘Intersection-free rigid body dynamics’, ACM Transactions on Graphics, 40(4), art. 183, pp. 1–16. doi: 10.1145/3476576.3476773.

12. Flores, P. (2022) ‘Contact mechanics for dynamical systems: A comprehensive review’, Multibody Syst. Dyn., 54, pp. 127–177. doi: 10.1007/s11044-021-09803-y.

13. Vyatkin, S.I., Dolgovesov, B.S. (2022) ‘Methods of interactive modeling and visualization of functionally defined objects for 3D WEB applications’, Avtometriya, 58(1), pp. 111–118 (in Russ.). doi: 10.15372/AUT20220112.

14. Vyatkin, S.I., Dolgovesov, B.S., Korsun, A.S. (2003) ‘Detecting the collision of functionally defined objects with recursive division of object space’, Avtometriya, 39(6), pp. 119–126 (in Russ.).

15. Vazquez, M.B., Pereira-Saez, M.J., Rodriguez-Raposo, A.B., Souto-Salorio, M.J. (2022) ‘Contact detection be-tween a small ellipsoid and another quadric’, Comput. Aided Geometric Design, 98, art. 102136. doi: 10.1016/ j.cagd.2022.102136.

16. Li, Y., Asai, M., Chandra, B., Isshiki, M. (2020) ‘Energy-tracking impulse method for particle-discretized rigid-body simulations with frictional contact’, Computational Particle Mechanics, 8, pp. 237–258. doi: 10.1007/s40571-020-00326-5.