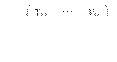Программная реализация диагностики непрерывных многостадийных производств с использованием динамической экспертной системы
| Меркурьев С.А. (serj.merkur@yandex.ru) - Тверской государственный технический университет, Тверь, Россия, Аспирант , Палюх Б.В. (pboris@tstu.tver.ru) - Тверской государственный технический университет (профессор), г. Тверь, Россия, доктор технических наук, Ветров А.Н. (vetrov_48@mail.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, кандидат технических наук | |
| Ключевые слова: точка бифуркации, диагностика, динамические экспертные системы, прикладные системы искусственного интеллекта |
|
| Keywords: bifurcation point, diagnostics, dynamic expert systems, applied artificial intelligence systems |
|
|
|
|
Введение. В данной статье поднимается проблема диагностики непрерывных многостадийных производств. К ним можно отнести процессы химической промышленности, атомной энергетики, металлургии и т.п. Многие из этих процессов потенциально опасны. Одной из важных задач управления такими процессами является обеспечение их стабильности. Для этого производится непрерывный мони- торинг состояния технологического процесса путем периодического измерения диагностических переменных и сравнения их с нормативными значениями. При штатной работе оборудования технологический процесс функционирует в стационарном режиме, но со временем оборудование физически и морально изнашивается. В ходе этого процесса технологический процесс постепенно переходит в нестационарный режим и становится неуправляемым. Время обнаружения аномального поведения технологического процесса существенно влияет на способность системы к восстановлению. Проблема обнаружения аномалий в сложных динамических системах является разви- вающейся областью научных исследований и активно обсуждается в литературе (напри- мер, [1, 2]). В проведенных исследованиях в области обнаружения и диагностики аномальных событий подчеркивается, что вопросы раннего предупреждения об опасной ситуации являются очень актуальными [3, 4]. Традиционно обнаружение аномалий относится к проблеме выявления паттернов в данных, полученных на основе мониторинга деятельности системы, которые не соответствуют ожидаемому поведению. Эти несоответствующие паттерны часто называют аномалиями. Системы обнаружения аномалий во временных рядах используются в самых разных приложениях [5, 6]. Проблема поиска аномалий интерпретируется как проблема классификации. Для ее решения используются методы классификации, такие как метод k-ближайшего соседа, кластерный анализ, классификаторы, построенные с использовани- ем искусственных нейронных сетей, метод случайного леса и т.п. [7, 8]. Хотя существующие системы поиска аномалий во временных рядах доказали свою эффективность, существует ряд проблем, связанных с их практическим применением: высокий уровень ложных срабатываний, ограниченные типы аномалий, которые система может обнаружить. Кроме того, такие системы не могут выполнять обнаружение аномалий в реальном времени. Наиболее существенным недостатком с точки зрения определения бифуркаций в непрерывных многостадийных технологических процессах является необходимость предварительного обучения рас- смотренных систем поиска аномалий. Посколь- ку аварийные ситуации относятся к классу редких событий, формирование БД для обучения проблематично. В настоящее время на непрерывных многостадийных производствах зачастую, используются только базовые системы мониторинга технологического процесса путем периодического измерения диагностических переменных и сравнения их с нормативными значениями. Решению проблемы диагностики многостадийных производств и прогнозирования отказов и аварийных ситуаций посвящены работы ряда российских исследователей. Так, в [9] пред- ложена композиционная модель прогнозирования аварийных ситуаций. Она осуществляет прогнозирование аварийных ситуаций, включая долгосрочный и текущий прогнозы. Долгосроч- ный прогноз основывается на термодинамической модели, а текущий – на лингвистической и нейросетевой моделях, при этом в ситуациях, не предусмотренных обучающими выборками, предпочтение отдается нейросетевой модели. Предлагаемая экспертная система позволяет совместить долгосрочный и текущий прогно- зы, обучение системы осуществляется автоматически, что повышает эффективность прогнозирования диагностических процедур. В статье [10] поднимается вопрос совершенствования процесса управления региональной безопасностью за счет развития методов анализа данных о чрезвычайных ситуациях. Авторами предложена многомерная классификация данных в области чрезвычайных ситуаций на основе нечеткой логики, которую нельзя применить для отдельного технологического процесса. В данной статье рассмотрен разрабатываемый программный комплекс экспертной системы ExpSystem, которая совмещает в себе методы экспертного и количественного ана- лиза состояния технологического процесса в условиях неопределенности. Экспертная система ExpSystem позволяет не только обнаруживать и диагностировать переход технологического процесса в нестационарное состояние, но и определять причину возникновения аномалии, находить дефектное оборудование, являющееся источником критической ситуации. Отличительной особенностью ExpSystem является использование метода двойного скользящего окна для определения момента бифуркаций и формирование гипотез о причинах кризисных состояний технологического процесса с помощью функции доверия. Назначение программного комплекса
В качестве входных параметров рассматривается матрица D(d, k) потоковых данных на момент времени T. Наблюдения осуществляются через равные промежутки времени Δt (или с частотой f = 1/ Δt):
где d – количество датчиков в системе; k – количество временных срезов до момента времени T. Далее эта матрица с данными поступает на вход первого модуля динамической экспертной системы ExpSystem. Задачей этого модуля является обнаружение аномалий и определе- ния момента бифуркации на основе метода двойного скользящего окна по каждому датчику. На выходе получаем массив R(d) с логическими переменными, которые обозначают факт наличия точки бифуркации в потоке данных с датчика d. Задачей второго модуля является формирование гипотез о причинах кризисных состояний с помощью функций доверия на основе массива R(d). Дальше эта информация поступает в третий модуль, где агент-координатор технологического процесса с помощью полученной информации определяет неработоспособную цепь производства, и с помощью наводящих вопросов экспертная система определяет место дефекта и возможные действия для его устранения. Результат этого анализа передается агентам (операторам), целью которых будет принятие решений функционирования приведения оборудования технологической цепи в стационарный режим. Интеграционная схема программного комплекса представлена на рисунке 2. Модуль обнаружения аномалий и определения момента бифуркации Перед первым модулем ставится задача обнаружения аномалий и определения момента бифуркации на основе анализа многомерного потока данных. На вход первого модуля подается матрица D(d, k). Для определения точки бифуркации предлагается метод двойного скользящего окна, суть которого заключается в проверке условий стационарности на основе выборочных данных для коротких временных рядов [11].
Работа алгоритма заключается в определении наличия точки бифуркации для каждого потока данных с датчика D(d, k), где d – количество датчиков в системе; k – количество временных срезов. С этой целью для каждого потока данных каждого датчика необходимо выполнить определенные этапы. Этап 1. Входной массив данных делится на N равных кортежей длины h. Этап 2. Для каждого получившегося кортежа выполняются следующие действия: · применяется алгоритм первого скользящего окна, которое используется как низкочастотный фильтр, подавляющий кратковременные случайные выбросы значений диагностических переменных; · вычисляются средние · получившиеся значения записываются во второе скользящее окно. Этап 3. После анализа всех кортежей считаются статистические параметры. Для этого за- писанные во второе скользящее окно значения проверяются на наличие тренда с помощью модификации критерия Фостера–Стюарда и рассчитываются множества un и vn по формулам
Затем вычисляют две статистики W и F:
и значения
где
После проверяется гипотеза об отсутствии стационарности. При отсутствии тренда нормализованные значения статистик приближенно описываются распределением Стьюдента с числом степеней свободы df = N. После анализа временных рядом в диагностических переменных от каждого датчика проверяем, были ли обнаружены бифуркации. Если они не были найдены, то система ожидает поступления новых данных. При нахождении бифуркаций система приступает к последующим этапам анализа по второму и третьему модулям. Модули формирования гипотез о причинах критических состояний и логического вывода Второй модуль основан на применении теории Демпстера–Шафера с целью формирования гипотез о причинах кризисных состояний технологического процесса. Теория свидетельств, или теория Демпстера–Шафера, является общей основой для рассуждений с неопределенностью и позволяет объединить свидетельства из разных источников и прийти к некоторой степени уверенности в наличии того или иного события [12–14]. Логика данного модуля подробно рассмотрена в [15]. Для его работы используются данные, полученные из предыдущего модуля, и данные из базы знаний. В третьем модуле логического вывода по диагностике многостадийного производства реализована экспертная система [16]. С помощью системы и сформированных гипотез агент-координатор выявляет неисправную технологическую цепь и уточняет дефект. После этого он передает полученную информацию агентам-технологам для корректирования состояния или остановки технологического процесса. Используемые инструментальные средства Данный программный комплекс разработан с помощью объектно-ориентированного языка программирования C#. Известно, что язык C# является мощным и гибким объектно-ориентированным языком программирования с поддержкой современных технологий, таких как LINQ и асинхронное программирование. Он также предлагает высокую производительность, что важно для эффективного выполнения сложных операций. Это делает его идеальным выбором для разработки сложных программных комплексов. Моделирование данных в первом модуле реализовано с помощью сторонней програм- мной системы AnyLogic, в которой была построена соответствующая модель. Формирование гипотез в третьем модуле реализовано с помощью программной среды для разработки экспертных систем CLIPS и набора продукционных правил, загруженных из базы знаний. Заключение Фундаментальная проблема обеспечения устойчивости системы управления эволюцией непрерывных многостадийных процессов к воз- никающим критическим ситуациям актуальна. В ней недостаточно проработаны методы раннего обнаружения момента перехода технологического процесса из штатного режима в пред- аварийное состояние. В статье рассмотрен программный комплекс, который использует новый подход для выявления начала переходного процесса в системе управления, а также моделирует состояние технологического процесса в ближайшем будущем. Это позволяет не только узнавать о критическом состоянии технологического процесса в текущий момент времени, но и предсказывать его состояние, благодаря чему появляется возможность заблаговременно проанализировать ситуацию и принять правильные решения. В конечном итоге это позволит избежать не только затрат на восстановление производства в случае аварийной ситуации, но и простоев в работе производства. Список литературы 1. Zhang Y., Chen Y., Wang J., Pan Z. Unsupervised deep anomaly detection for multi-sensor time-series signals. IEEE Transactions on Knowledge and Data Engineering, 2021, vol. 35, no. 3, pp. 2118–2132. doi: 10.1109/TKDE.2021.3102110. 2. He Y., Zhao J. Temporal convolutional networks for anomaly detection in time series. JPCS, 2019, vol. 1213, art. 042050. doi: 10.1088/1742-6596/1213/4/042050. 3. Kim D., Yang H., Chung M. et al. Squeezed Convolutional Variational AutoEncoder for unsupervised anomaly detection in edge device industrial Internet of Things. Proc. ICICT, 2018, pp. 67–71. doi: 10.1109/INFOCT.2018.8356842. 4. Zhao H., Wang Y., Duan J. et al. Multivariate time-series anomaly detection via graph attention network. ICDM, 2020, pp. 841–850. doi: 10.1109/ICDM50108.2020.00093. 5. Li D., Chen D., Jin B. et al. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In: ICANN. LNTCS, 2019, vol. 11730, pp. 703–716. doi: 10.1007/978-3-030-30490-4_56. 6. Lin S., Clark R., Birke R., Schonborn S., Trigoni N., Roberts S. Anomaly detection for time series using VAE-LSTM hybrid model. Proc. ICASSP, 2020, pp. 4322–4326. doi: 10.1109/ICASSP40776.2020.9053558. 7. Su Y., Zhao Y., Niu C., Liu R., Sun W., Pei D. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. Proc. KDD, 2019, pp. 2828–2837. doi: 10.1145/3292500.3330672. 8. Chen Z., Chen D., Yuan Z., Cheng X., Zhang X. Learning graph structures with transformer for multivariate time series anomaly detection in IoT. IITJ, 2022, vol. 9, no. 12, pp. 9179–9189. doi: 10.1109/JIOT.2021.3100509. 9. Ткалич С.А. Инструментальная методика прогнозирования аварийных ситуаций технологических процессов // Вестн. РГРТУ. 2022. № 79. С. 101–113. 10. Лабинский А.Ю., Бородушко И.В., Таранцев А.А. Поддержка принятия управленческих решений при рисках чрезвычайных ситуаций на основе применения методов анализа многомерных статистических данных // Инженерный вестник Дона. 2023. № 10. URL: http://www.ivdon.ru/uploads/article/pdf/IVD_20__10_Labinskiy_Boro-dushko_Tarantsev.pdf_a6205847c7.pdf (дата обращения 10.04.2024). 11. Ветров А.Н., Мальков А.А., Палюх Б.В. Детектирование бифуркаций многомерных случайных процессов в динамических экспертных системах // КИИ: тр. конф. 2023. С. 173–182. 12. Ullah I., Youn J., Han Y.-H. Multisensor data fusion based on modified belief entropy in Dempster–Shafer theory for smart environment. IEEE Access, 2021, vol. 9, pp. 37813–37822. doi: 10.1109/ACCESS.2021.3063242. 13. Jiroušek R., Kratochvíl V., Shenoy P.P. Entropy for evaluation of Dempster–Shafer belief function models. IJAR, 2022, vol. 151, pp. 164–181. doi: 10.1016/j.ijar.2022.09.009. 14. Zhang C., Chen K., Zeng X., Xue X. Misbehavior detection based on support vector machine and Dempster–Shafer theory of evidence in VANETs. IEEE Access, 2018, pp. 59860–59870. doi: 10.1109/ACCESS.2018.2875678. 15. Иванов В.К., Виноградова Н.В., Палюх Б.В., Сотников А.Н. Современные направления развития и области приложения теории Демпстера–Шафера // ИИиПР. 2018. № 4. С. 32–42. doi: 10.14357/20718594180403. 16. Shabanov B., Sotnikov A., Palyukh B., Vetrov A., Alexandrova D. Expert system for managing policy of technological security in uncertainty conditions: Architectural, algorithmic, and computing aspects. Proc. ElConRus, 2019, pp. 1716–1721. doi: 10.1109/EIConRus.2019.8657114. References 1. Zhang, Y., Chen, Y., Wang, J., Pan, Z. (2021) ‘Unsupervised deep anomaly detection for multi-sensor time-series signals’, IEEE Transactions on Knowledge and Data Engineering, 35(3), pp. 2118–2132. doi: 10.1109/TKDE.2021.3102110. 2. He, Y., Zhao, J. (2019) ‘Temporal convolutional networks for anomaly detection in time series’, JPCS, 1213, art. 042050. doi: 10.1088/1742-6596/1213/4/042050. 3. Kim, D., Yang, H., Chung, M. et al. (2018) ‘Squeezed Convolutional Variational AutoEncoder for unsupervised anomaly detection in edge device industrial Internet of Things’, Proc. ICICT, pp. 67–71. doi: 10.1109/INFOCT.2018.8356842. 4. Zhao, H., Wang, Y., Duan, J. et al. (2020) ‘Multivariate time-series anomaly detection via graph attention network’, ICDM, pp. 841–850. doi: 10.1109/ICDM50108.2020.00093. 5. Li, D., Chen, D., Jin, B. et al. (2019) ‘MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks’, in ICANN. LNTCS, 11730, pp. 703–716. doi: 10.1007/978-3-030-30490-4_56. 6. Lin, S., Clark, R., Birke, R., Schonborn, S., Trigoni, N., Roberts, S. (2020) ‘Anomaly detection for time series using VAE-LSTM hybrid model’, Proc. ICASSP, pp. 4322–4326. doi: 10.1109/ICASSP40776.2020.9053558. 7. Su, Y., Zhao, Y., Niu, C., Liu, R., Sun, W., Pei, D. (2019) ‘Robust anomaly detection for multivariate time series through stochastic recurrent neural network’, Proc. KDD, pp. 2828–2837. doi: 10.1145/3292500.3330672. 8. Chen, Z., Chen, D., Yuan, Z., Cheng, X., Zhang, X. (2022) ‘Learning graph structures with transformer for multivariate time series anomaly detection in IoT’, IITJ, 9(12), pp. 9179–9189. doi: 10.1109/JIOT.2021.3100509. 9. Tkalich, S.A. (2022) ‘Instrumental methodology for predicting emergency situations of technological processes’, Vestn. of RSREU, (79), pp. 101–113 (in Russ.). 10. Labinskiy, A.Yu., Borodushko, I.V., Tarantsev, A.A. (2023) ‘Support for managerial decision-making in case of emergency risks based on the use of methods of analysis of multidimensional statistical data’, Engineering J. of Don, (10), available at: http://www.ivdon.ru/uploads/article/pdf/IVD_20__10_Labinskiy_Borodushko_Tarantsev.pdf_a6205847c7.pdf (accessed April 10, 2024) (in Russ.). 11. Vetrov, A.N., Malkov, A.A., Palyukh, B.V. (2023) ‘Detection of bifurcations of multidimensional random processes in dynamic expert systems’, Proc. CAI, pp. 173–182 (in Russ.). 12. Ullah, I., Youn, J., Han, Y.-H. (2021) ‘Multisensor data fusion based on modified belief entropy in Dempster–Shafer theory for smart environment’, IEEE Access, 9, pp. 37813–37822. doi: 10.1109/ACCESS.2021.3063242. 13. Jiroušek, R., Kratochvíl, V., Shenoy, P.P. (2022) ‘Entropy for evaluation of Dempster–Shafer belief function models’, IJAR, 151, pp. 164–181. doi: 10.1016/j.ijar.2022.09.009. 14. Zhang, C., Chen, K., Zeng, X., Xue, X. (2018) ‘Misbehavior detection based on support vector machine and Dempster–Shafer theory of evidence in VANETs’, IEEE Access, pp. 59860–59870. doi: 10.1109/ACCESS.2018.2875678. 15. Ivanov, V.K., Vinogradova, N.V., Palyukh, B.V., Sotnikov, A.N. (2018) ‘Current trends and applications of Dempster–Shafer theory (review)’, AIDT, (4), pp. 32–42 (in Russ.). doi: 10.14357/20718594180403. 16. Shabanov, B., Sotnikov, A., Palyukh, B., Vetrov, A., Alexandrova, D. (2019) ‘Expert system for managing policy of technological security in uncertainty conditions: Architectural, algorithmic, and computing aspects’, Proc. ElConRus, pp. 1716–1721. doi: 10.1109/EIConRus.2019.8657114. |
http://swsys.ru/index.php?id=5127&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Общие принципы системной оптимизации технологии контроля качества телерадиопродукции
- Экспертная система мониторинга технологического процесса
- Системный анализ и принятие решений о реинжиниринге корпоративных информационно-управляющих систем
- Прототип диагностической системы поддержки принятия решений на основе интеграции байесовских сетей доверия и метода Демпстера–Шефера
- Модели управления транспортными потоками в условиях затора