Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Методика оценки точности нейросетевых моделей
Аннотация:
Abstract:
| Авторы: Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук, Котельников С.А. () - | |
| Ключевые слова: нейросетевое моделирование, закон распределения, вычислительный эксперимент |
|
| Keywords: neural network modeling, the law of distribution, computing experiment |
|
| Количество просмотров: 15579 |
Версия для печати Выпуск в формате PDF (1.83Мб) |
В практике нейросетевого моделирования часто возникает задача оценки точности получаемых моделей [1-3]. Рассмотрим задачу нейросетевого моделирования в следующей постановке. Пусть имеется статический объект, имеющий n входов (векторный вход
где Необходимо построить нейросетевую модель данного статического объекта (оценку функции
и оценить точность полученной модели. Задача оценки точности модели решается следующим образом. Обучающая выборка (2) случайным образом делится на собственно обучающую:
по которой и проводится обучение нейронной сети, и тестирующую: (объем тестирующей выборки (4) выбирается обычно во много раз меньше объема обучающей выборки (3), то есть Рассмотрим ошибки модели: где Ввиду наличия случайного шума
где Точечные оценки
где Описанные точечные оценки Интервальные оценки точности моделей. Для конкретизации метода построения интервальных оценок необходимо проверить гипотезу нормальности распределения величины Сведем результаты опытов в L интервалов и оформим в виде статистического ряда (см. табл. 1). Таблица 1
В таблице приняты следующие обозначения: На основе функции нормального закона распределения можно найти теоретические вероятности попадания в каждый интервал:
Проверка согласованности нормального и статистического распределений производится на основе анализа расхождения между теоретическими вероятностями
Распределение где R – число независимых условий (связей). Если выполняется условие 1. Гипотеза нормальности распределения величины Доверительный интервал для ошибки модели
где Воспользовавшись свойствами распределенной по нормальному закону случайной величины, получим оценку максимальной абсолютной ошибки модели Maxd с доверительной вероятностью; b1 – доверительная вероятность, использующаяся при проверке гипотезы нормальности закона распределе- ния [4,5]: Верхняя оценка значения СКО ошибки модели где 2. Гипотеза нормальности На основании неравенства Чебышева можно записать:
где Проведя преобразования на основе (16), можно получить доверительный интервал для ошибки модели
где В случае, когда для закона распределения случайной величины
Метод проверки гипотезы симметричности закона распределения случайной величины описан в работе [6]. Для получения верхней оценки значения СКО модели
где Вычислительный эксперимент. Выполним построение нейросетевых моделей и оценку их ошибки для объектов со структурой (1), описываемых следующими выражениями:
где Для построения моделей использовались следующие методы: обобщенно-регрессионная нейронная сеть (GRNN), многослойный персептрон (MLP), сеть с радиальными базисными функциями и линейным выходным слоем (RBFN) [1-3]. Объем обучающей выборки составлял N=2900 (N1=2500, N2=400). Точки из обучающей выборки располагались случайным образом с равномерным законом распределения. Результаты вычислительного эксперимента приведены в таблице 2. Таблица 2
Рассмотренный подход к оцениванию точности моделей может быть полезен при нейросетевом моделировании. Современные системы компьютерной математики (MATLAB, MathCAD, Maple и др.) имеют набор встроенных статистических функций, что позволяет значительно упростить процессы как проверки гипотезы нормальности распределения, так и построения описанных интервальных оценок. Список литературы 1.Галушкин А.И. Теория нейронных сетей. - М.: ИРПЖР. - Кн.1. - 2000. 2.Галушкин А.И. Нейрокомпьютеры. - Там же. - Кн.3. - 2000. 3.Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Горячая линия-телеком, 2001. 4.Венцель Е.С. Теория вероятностей. – М.: Высш. шк., 1998. 5.Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1984. 6.Орлов А.И. Методы проверки однородности связных выборок // Заводская лаборатория. - 2004. - Т.70. - №7. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?id=750&like=1&page=article |
Версия для печати Выпуск в формате PDF (1.83Мб) |
| Статья опубликована в выпуске журнала № 2 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Возможности прогнозирования динамики фондового индекса S&P 500 с помощью нейросетевых и регрессионных моделей
- Построение архитектуры САПР одношнековых экструдеров с применением элементов искусственного интеллекта
- Использование программного обеспечения для определения и прогнозирования показателей качества экструдированной продукции
- Прогнозирование времени обработки изображений детерминированными методами
- Активная идентификация автоматизированных систем на основе вычислительного эксперимента
Назад, к списку статей



 . (10)
. (10)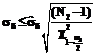 , (15)
, (15)
