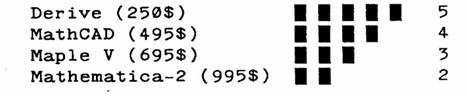Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Сравнительный анализ зарубежных интегрированных систем компьютерной алгебры
Аннотация:
Abstract:
| Авторы: Дьяконов В.П. () - , Найденов В.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 13360 |
Версия для печати |
Общие сведения о системах символической математики. В такой серьезной сфере применения ПК, как математические расчеты, в последние годы наметился огромный прогресс. Наряду с программами для калькуляторов и программами на обычных языках программирования [1, 2] становятся доступными десятки интегрированных математических систем: Eureka, MathCAD, MatLAB, TK Solver Plus, Derive, Maple V, Mathematica-2 и др. [З - 8]. Среди них особое место занимают системы символической математики (компьютерной алгебры). Эти системы облегчают, а подчас и заменяют труд научной элиты - математиков-аналитиков. В Смоленском областном центре новых информационных технологий проведен сравнительный анализ четырех наиболее известных зарубежных интегрированных математических систем компьютерной алгебры, описанных в [8]: Derive 2.1 фирмы Soft Warehouse Inc., MathCAD 3.0/4.0 для Windows фирмы MathSoft Inc., Maple V 1.1 фирмы Waterloo Maple Software, Mathematica-2.1 для Windows фирмы Wolfram Research Inc. Результаты анализа описаны в этой статье. Для оценки избрана пятибалльная шкала. Баллы несут не более чем сравнительные оценки, помогающие (вместе с их обоснованием) оптимально выбрать математическую систему по 14 критериям. Аппаратные ресурсы - не главное в оценке систем. Однако предпочтение можно отдать системам, не предъявляющим к аппаратным ресурсам жестких требований:
Стоимость системы. При приобретении систем легальным путем немаловажное значение имеет их стоимость. Чем она ниже, тем выше балл:
Полнота ядра символьных операций фактически подразумевает число встроенных в ядро функций и алгоритмов символьных преобразований. Оценка: У лидеров - системы Maple V - в ядре около 2000 всевозможных функций (с различными их модификациями). Неплохо представлены и алгоритмы математических преобразований. Ядро MathCAD 3.0/4.0 - это резко сокращенная версия ядра Maple V. Рисунок 1 показывает выполнение символьных операций в новейшей системе MathCAD 4.0 с применением средства SmartMath визуализации символьных преобразований. Это средство позволяет также оптимизировать многие численные расчеты, заменив вычисления по численным алгоритмам вычислениями по полученным в ходе символьного преобразования формулам. . Достаточно полным является и ядро системы Mathematica-2. Однако по числу функций (около 800, не считая слов-определений) эта система все же уступает Maple V. Ядро Derive недосчитывает многие специальные математические функции (впрочем, при решении задач, не требующих их применения, ущербности ядра Derive не ощущается). Однако наиболее распространенные преобразования Derive выполняет без каких-либо подсказок как нечто само собой разумеющееся. Полнота системы. Под полнотой системы будем подразумевать ее возможности с учетом возможностей не только ядра, но и всех внешних библиотек и пакетов применений (Application Cards).
Maple V и Mathematica-2 имеют богатейшие библиотеки и заслуживают высшего балла. Куда скромнее библиотеки Derive, хотя и они поражают богатством расширений. MathCAD заслужил самый низкий балл потому, что его пакеты применений поставляются отдельно и стоят (для 10 пакетов) вдвое дороже, чем сама система.
Рис.1. Символьные операции в среде MathCAD 4.0 Рис.2. Трехмерная графика в среде Mathematika-2
Рис.3. Трехмерная и контурная графика в среде MathCAD 4.0
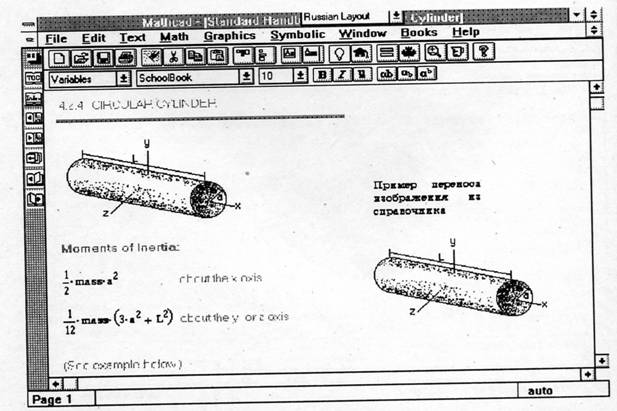
Рис.4. Получение информации из стандартного справочника системы MathCAD 4.0 Производительность систем для простых операций. Наивысшей оценки заслуживает система Derive, которая почти мгновенно выдает результаты при простых тестовых примерах. Хорошей следует признать производительность системы MathCAD. Система Maple V могла бы заслужить оценку 3.5, но мы вынуждены использовать целочисленные оценки - в сравнении с MathCAD она работает все же медленнее. Далеко не лучшим образом приходится оценить систему Mathematica-2 - это единственная система, которая работает удручающе медленно на ПК с ОЗУ 4 Мбайта. Однако при сложных вычислениях ситуация может оказаться совсем иной. Итак, оценки таковы:
Достоверность решения. Наша оценка достоверности решений подобна [6]:
Согласно [6] в 20 тестовых задачах ни одна из систем не дала всех правильных результатов. Это исключает отличную оценку. Бесспорным лидером оказалась система Derive - она не сумела вычислить сложный аналитический интеграл, отказавшись от его вычислений. Derive требует минимума подсказок при решении типовых задач символической математики. Система Maple V тоже показала себя неплохо - лишь в одном случае она дала неверный результат, а в двух других для решения пришлось составлять программы, намечающие путь к истине. Система Mathematica-2 тут явно "оскандалилась" - одну из задач решила неверно, а для трех ответа вообще не удалось получить. Поскольку ядро MathCAD 3.0 базируется на сильно урезанном ядре системы Maple V, мы оценили систему по этому критерию баллом ниже, чем Maple V. Графические возможности. Оказалось, что чем мощнее система, тем больше графических возможностей она предоставляет:
Mathematica-2 здесь общепризнанный лидер. Она имеет богатейший набор графических функций для построения 2D- и ЗD-графиков, контурных диаграмм и многих геометрических фигур с богатейшей цветовой гаммой изображений (рис. 2). При просмотре графиков объемных фигур (3D) имеется возможность изменения углов просмотра. Поддерживаются даже средства мультимедиа (анимация изображений и плата Sound Blaster). Графика Maple V великолепна! Но она все же не обладает всеми возможностями графики Mathematica-2. Поэтому ее оценка на балл ниже. Неплохо реализована стандартная математическая графика в системе MathCAD. В новейшей версии MathCAD 4.0 появились возможности построения графиков в полярных координатах, контурных диаграмм и ЗО-поверхностей с весьма привлекательными алгоритмами функциональной закраски (рис. 3). Графика системы Derive куда проще. Впрочем, в ряде случаев система реализует многооконный режим, позволяет строить графики функций разного вида (2D, 3D и в полярных координатах) и сочетает в разных окнах графики с математическими текстами. Построение контурных диаграмм и раскраска трехмерных фигур не предусмотрены. Интерфейс пользователя. Под этим критерием мы подразумеваем наличие средств, с помощью которых работа с системой становится очевидной и наглядной. Это относится к наличию современных меню и базы данных помощи, а также к возможности управления мышкой. Наши оценки:
Лишь система MathCAD (особенно 4.0) заслуживает отличной оценки. Она является единственной не только имеющей все возможности Windows (многооконный режим, удобные меню, пиктограммы основных операций и т.д.), но и обеспечивающей подготовку документов в подлинно естественном математическом виде в стиле Notebook (блокнот), например: в этой системе математические знаки, такие как квадратный корень, знаки интеграла, суммы и произведения и т.д. отображаются в своем естественном виде и сочетаются с графиками любого размера, расположенными в любом месте. Прекрасно реализовано управление системой от мышки. Реализация стиля Notebook в системе Mathematica-2 пока явно не доработана: каждая ячейка занимает полную строку, представление математических символов в естественном виде отсутствует, в пределах ячейки допустим лишь один стиль символов и комментарий. Работа с мышкой менее эффективна. Интерфейс у системы Derive удручающе примитивен. Ее меню постоянно присутствует в нижней части экрана. Более того, при снятии твердых копий графических результатов копируется теперь уже совсем не нужное меню графических операций. Работу с мышкой система Derive не поддерживает. Интерфейс Maple V архаичен. Однако есть возможность вызова предыдущего сеанса работы с возможностью выделения его фрагмента и его переноса в нужное место. Maple V с мышкой не работает. Работа в режиме калькулятора. Пользователь, купивший математическую систему, вправе рассчитывать на то, что ему не надо будет при работе с ней держать под рукой калькулятор. Однако все не так просто: численные расчеты — подлинная обуза для систем символической математики. Оценки же таковы:
Кроме системы Mathematica-2, все остальные заслуживают высшей оценки. Балл для Mathematica-2 снижен: ее особый синтаксис затрудняет проведение расчетов в общепринятом виде. Возможности редактирования документов. В ходе сеанса работы с системой (сессией) готовятся документы, содержащие текстовые сообщения, математические формулы, рисунки и таблицы. Их приходится постоянно редактировать с целью исправления ошибок или придания документам наиболее наглядного вида. Возможности редактирования можно оценить следующим образом:
Здесь в худшем положении система Derive. Она имеет только простейший строковый редактор. MathCAD, напротив, заслуживает высшей оценки — возможности редактирования здесь прекрасны и можно эффектно пользоваться мышкой. Чуть хуже эти возможности реализованы в системе Mathematica-2. Maple V недалеко ушла от Derive. Редактирование идет в текущей строке. Однако Maple V содержит встроен? ный текстовой редактор, в который можно поместить выделенный кусок документа или начать в нем подготовку нового. База данных помощи. С математическими системами, даже приобретенными легально, многие вынуждены работать без документации. К примеру, если кафедра вуза или лаборатория НИИ приобрели такую систему, то вряд ли все пользователи имеют доступ и к документации. Кроме того, большинство пользователей предпочитает работу в системе просмотру документации, подчас насчитывающей не одну тысячу страниц. Поэтому для работы с системой важно наличие в ней базы данных помощи. Оценка по этому показателю такова:
MathCAD заслуживает высшей оценки, поскольку ее база данных помощи построена не только с присутствием всех возможностей Windows, но и с наличием откровенного желания разработчиков подробно ознакомить пользователей со всеми возможностями системы. К услугам пользователя подробные меню, система поиска нужных слов, развернутая информация обо всех возможностях системы. Системе MathCAD 4.0 так и хочется выставить 5 с плюсом! Это единственная система, в которую встроены три справочные книги и самоучитель по системе (рис. 4). Система помощи Maple V выполнена более примитивно. Зато из подсказки можно вырезать любой фрагмент (например сразу несколько тестовых примеров или целую программу), перенести их в рабочее окно и тут же исполнить. Версия 2.0 системы Mathematica не имее базы данных по ядру, и это серьезный недоста ток (без документации с такой системой рабе тать вообще нельзя). Он устранен уже в расши ренной версии 2.1. К сожалению, число приме ров применения функций в базе данных помощ! этой системы очень мало, а на многие функции их просто нет. Это заметно снизило наш; оценку. Система помощи Derive крайне примитивна - это просто список команд и функций с их названиями. Никаких примеров применения функций нет, хотя кратко представлен их синтаксис. Практические примеры (пакеты применений). При освоении систем немаловажное значение имеет наличие практических примеров применения систем. Здесь оценка такова:
Несомненным лидером здесь является система Maple V. По каждой из многих сотен ее функций система в базе данных помощи дает несколько примеров применений. Их общее число приближается к 10 000. MathCAD содержит пару десятков наглядных примеров. Неплохо представлен набор примеров и в системе Derive - примеров много, они достаточно просты и наглядны. Примеры для Mathematica-2 даны в виде файлов в каталоге NOTEBOOK. Эти примеры в первую очередь призваны продемонстрировать мощь системы - прекрасную графику (в том числе с режимом анимации) и возможность выполнения сложных вычислений. Примеры очень сложны и нередко преднамеренно даны в режиме скрытия деталей вычислений. Разобраться с ними сложно. Это дало нам повод серьезно снизить оценку по данному показателю этой системе. Язык программирования. Большинство математических систем сводят к минимуму необходимость программирования задач, решаемых пользователем. Однако для расширения систем, особенно опытными пользователями, в них вводят язык программирования сверхвысокого уровня, ориентированный на решение математических задач. Оценка языка:
Система Mathematica-2 имеет наиболее развитый язык программирования. Он содержит полный набор управляющих структур и многочисленные средства как низкого уровня (работа с памятью и дисками), так и высокого и даже сверхвысокого уровня (обращение к любым функциям ядра). Язык программирования системы Maple V несколько уступает ему, но тоже превосходен. Средства управления вычислительным процессом у MathCAD (и тем более у Derive) с трудом можно отнести к понятию языков программирования. Безаварийность работы. Наши оценки по безаварийности математических систем выглядят следующим образом:
Derive - довольно надежная система. Ее недостаток - отсутствие поддержки расширенной памяти современных ПК. Поэтому при решении сложных задач нередко можно столкнуться с сообщением о нехватке памяти. Нам не удалось ни разу отметить сбоев в работе систем MathCAD и Maple V. Это позволило выставить им максимальные баллы. Хуже всего ситуация оказалась с системой Mathematica-2.1 - неоднократно при ее освоении возникали фатальные ошибки (Fatal Errors) с предупреждением о выходе из сеанса работы с системой. Это приводило, как правило, к потере данных по текущему сеансу работы. Были нередки случаи зависания и даже перезагрузки системы, что вынуждает выставить балл 2 этой системе. Итоговая оценка. Итак, мы оценили системы по 14 довольно разным показателям. Можно ожидать, что ценность сравнения систем в основном определяется частными показателями, а вовсе не суммарной оценкой. Тем не менее, просуммировав все оценки и поделив их на 14, получим следующую итоговую оценку:
Результаты итоговой оценки неожиданны лишь на первый взгляд. Претендующая на роль лидера система компьютерной алгебры Mathematica-2 оказалась на последнем месте. Это говорит лишь об одном: эта сложная математическая система все еще требует серьезной доработки. На оценку существенно повлияли невысокая скорость работы системы для простых задач, низкая достоверность решения тестовых задач и подверженность авариям. Maple V имеет наивысшую оценку. Это вполне заслуженно, поскольку Maple V -тщательно апробированная развитая солидная система. Неплохую оценку заслужила система MathCAD 3.0/4.0. Однако она набрала итоговые баллы не за счет своих (довольно умеренных) математических способностей, а за счет превосходного интерфейса. Вновь, как и в случае с системой Maple V, на оценку лучшим образом повлияла отточенность системы за многие годы ее развития. Вклад в оценку внесло и включение в состав MathCAD 3.0/4.0 символьного процессора на базе сокращенного ядра Maple. Система Derive заслужила скромную оценку (хотя и выше Mathematica-2) вследствие примитивного интерфейса и скромных возможностей графики. Однако по возможностям ее ядра, скорости выполнения тестовых примеров и достоверности результатов Derive вполне заслуживает оценки "жемчужины символьной математики" [8]. Приведенные оценки позволяют обоснованно выбрать символические математические системы для нашего высшего образования. Очевидно, что лучшей здесь будет система Derive: имея довольно продвинутые средства компьютерной алгебры, она является самой дешевой системой и может работать на всех IBM-совместимых ПК. Система MathCAD 3.0/4.0 прекрасно подойдет для учебных классов на новом поколении ПК 386/486 с графической оболочкой Windows. Благодаря своему превосходному NOTEBOOK-интерфейсу эта система подходит для подготовки обучающих программ для курсов, интенсивно использующих математику. Система Maple V необходима для опытных пользователей - студентов старших курсов математических специальностей, аспирантов и преподавателей вузов. Несомненно, эта система должна быть в каждой лаборатории НИИ и на каждой кафедре, ведущих серьезные научные исследования. Новейшая система Mathematica-2.1 (1992 г.) пока наиболее интересна пользователям, основное направление работ которых связано с математической графикой (включая динамическую). Эта система интенсивно развивается, и есть надежда, что ее недостатки будут в ближайшее время устранены. Список литературы 1. Дьяконов ВЛ. Справочник по расчетам на микрокалькуляторах. - M.: Наука, Фиэматлит, 1989. - 464 с. 2. Дьяконов В.П. Справочник по алгоритмам и программам на языхе БЕЙСИК для персональных ЭВМ. - М.: Наука, Фиэматлит, 1987. - 240 с. 3. Дьяконов В.П. Справочник по применению системы Eureka. - M.: Наука, Фиэматлит, 1993. - 96 с. 4. Дьяконов В.П. Система MathCAD: Справочник. - M.: Радио и связь, 1993. - 128 с. 5. Дьяконов В.П. Справочник по применению системы PC MatLAB. - M.: Наука, Фиэматлит, 1993. - 112 с. 6. Барри Саймон. Символьная математика: новые времена - новые формы // PC Magazine (Россия). - 1992. - № 5-6. - C.29. 7. Дьяконов В.П. Общедоступные математические САПР для персональных компьютеров класса IBM PC // Программные продукты и системы. - 1993. -№ I,- СП. 8. Дьяконов В.П. Как выбрать математическую систему? // Монитор. Аспект. - 1993. - Л» 2. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1166 |
Версия для печати |
| Статья опубликована в выпуске журнала № 3 за 1994 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- О программной реализации геоинформационных систем
- Базовое программное обеспечение целостных компьютеризированных курсов в современной операционной обстановке
- Комплекс программных средств для аналитических иерархических процессов экспертного оценивания
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- Система визуализации реального времени на основе программируемых сигнальных процессоров
Назад, к списку статей