Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование температурных полей электронных блоков
Аннотация:
Abstract:
| Авторы: Решетников В.Н. (rvn_@mail.ru) - Центр визуализации и спутниковых информационных технологий ФНЦ НИИСИ РАН (профессор), Москва, Россия, доктор физико-математических наук, Мадера А.Г. (alexmadera@mail.ru) - НИИСИ РАН (профессор, зав. отделом), г. Москва, Россия, доктор технических наук, Сотников А.Н. (asotnikov@iscc.ru) - Федеральный исследовательский центр «Информатика и управление» РАН, ул. Вавилова, 44-2, г. Москва, 119333, Россия (главный научный сотрудник), г. Москва, Россия, доктор физико-математических наук, Резников Г.В. () - , Морозов А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 12955 |
Версия для печати |
Зависимость электрических параметров интегральных схем (ИС), электронных блоков с ИС и их надежности от температуры обусловливает необходимость моделирования распределения температуры электронного блока и его элементов. Основными элементами электронного блока являются печатная плата и установленные на ней ИС. Моделирование позволяет прогнозировать температурное поле печатной платы в различных ее точках, температуры корпусов и кристаллов ИС на этапе их проектирования. При моделировании теплового режима электронного блока должны учитываться основные элементы конструкции блока, различные механизмы и пути распространения тепловых потоков, в том числе отвод теплоты от поверхностей корпусов ИС в печатную плату через выводы корпуса кондукцией, отвод теплоты от печатной платы в элементы конструкций на плате, через тепловые и электрические разъемы, с поверхности платы в среду конвекцией и т.д. В настоящее время для отвода теплоты от И С в электронных блоках применяются различные варианты конструкций, использующие низкотемпературные тепловые трубы, каналы с протекающим холодоносителем, непосредственное жидкостное охлаждение [2]. Принудительное и естественное воздушное охлаждение электронных блоков также продолжает развиваться и применяться в современных вычислительных устройствах. Согласно [1,2] моделирование температурных полей объектов включает в себя: создание тепловой модели объекта; составление математической модели процес сов теплопереноса, протекающих в тепловой модели; решение уравнений математической модели; представление результатов в графическом и цифровом видах и их интерпретация. Тепловая модель электронного блока при воздушно-кондуктивном охлаждении состоит из двух взаимодействующих частей: - тепловой модели печатной платы с элемен тами, конструкции кондуктивного отвода теп лоты и крепления; - тепловой модели ИС. Тепловая модель платы представляет собой трехмерную пластину, на поверхности которой расположены прямоугольные источники и стоки теплоты, моделирующие тепловые потоки, поступающие в плату от ИС. Размеры источников теплоты равны размерам проекции корпуса ИС на плоскость платы. Контакт выводов корпуса с платой включается а область источника теплоты. Стоками теплоты моделируются конструкции, имеющие механический контакт с платой, через которую может осуществляться отток теплоты. Размеры стока теплоты равны соответствующим размерам контакта стока теплоты с платой. Принимается, что мощности в источниках и стоках теплоты равномерно распределены по их площади. Потерями теплоты с торцов платы будем пренебрегать. Тепловая модель ИС представляет собой тепловую схему (рис. 1), полученную методом аналогового моделирования. Мощность Q, потребляемая И С, рассеивается конструкцией корпуса ИС, моделируемой тепловым сопротивлением переход-корпус R . Часть потока теплоты от корпуса ИС передается в среду конвекцией, которая представляется тепловым сопротивлением корпус-среда R ; другая часть поступает в плату через выводы корпуса, моделируемые тепловым сопротивлением R и одновременно через зазор между корпусом ИС и платой, моделируемый тепловым сопротивлением R . Тепловой поток Q рассматривается на тепловой модели ИС источником тока; средние температуры кристалла t и корпуса ИС t является потенциалами в соответствующих узлах схемы; t — заданная температура среды; / - температура источника теплоты, усредненная по его площади.- Тепловое сопротивление R от корпуса в окружающую среду рассчитывается по формуле где а - коэффициент теплоотдачи в среду с поверхности корпуса ИС площадью 5, соприкасающейся со средой. Математическая модель процессов теплопередачи, протекающих в трехмерной пластине GeR , х — (х, х^ хр с границей AJ{X) + Р(х) = 0, хеС, (1) с граничными условиями х ^ - «/"■>= 0>хг °- (*,• х№0' 4 х 1°> *Ъ х%~ a2(lV = 0' x3^Ct ix,'x)^°'a'\ х [°. Ь1 (2) где а, b, с - размеры платы по осям х, х , х соответственно; а, а, - коэффициенты теплоотдачи с поверхностей платы; \ - коэффициент теплопроводности платы; А - оператор математической модели (1) Р(х) - суммарная функция источников и стоков теплоты где Р'{, Р"1 - объемные плотности мощностей источников и стоков теплоты на плате; A' h" -индикаторные функции, равные 1 в области источника и стока и-нулю вне областей источника стока; п, т - количество источников (ИС) и стоков теплоты. Рис. 2. Фрагмент структуры меню редактирования исходных данных Математическая модель i'-ой ИС на плате имеет вид i = I, 2, 3 ..., и, где Д' = RjRc^Rl + ДсР ~ тепловое СУМ" марное сопротивление между поверхностями корпуса ИС и платой; Р' - тепловой поток, поступающий от /-ой ИС в плату, в область /-го источника теплоты; t — температура окружающей среды около i'-ой ИС. Уравнения (1), (2), описывающие процессы теплопередачи в тепловой модели платы, могут решаться различными численными методами. Для рассматриваемой задачи может быть построена функция Грина в аналитическом виде. Тогда искомое температурное поле платы ((х), х~(х , х , x)eG + dG выражается через интеграл от функции Грина и функции источника Р(х), который легко вычисляется [1]. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ И РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ Программа моделирования стационарных температурных полей электронных блоков написана для IBM PC/AT на языке программирования ПАСКАЛЬ, версия 6.0 с использованием дополнительного пакета Turbo-Vision, с помощью которого обеспечивается диалог о пользователем. Процесс диалога с пользователем ведется с использованием следующих элементов: иерархического меню (рис. 2). С его помощью можно выбрать параметр элемента, подлежащий изменению; разнообразные сообщения, за-
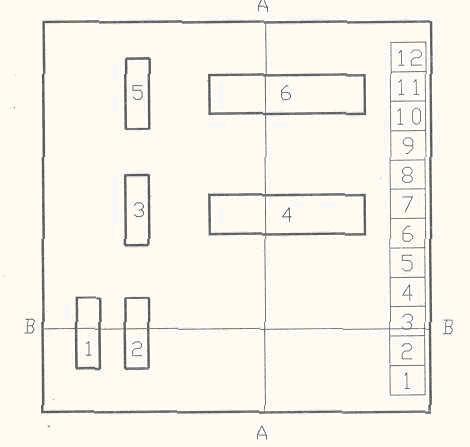
Рис, 3. просы; статусную строку, в которой выводятся сообщения о неких возможных действиях пользователя на данном этапе работы; контекстной помощи пользователю; вывода информации на экран дисплея с использованием окон (заметим, что цвет, размер, положение и взаимное положение окон могут быть изменены). При работе с меню, окнами, сообщениями выполнить любое действие можно как с использованием клавиатуры компьютера, так и с помощью устройства типа "мышь". Основные команды могут быть выполнены по нажатии определенной комбинации клавиш без использования меню. В случае, если при работе возникли затруднения, можно получить подсказку, нажав клавишу F1, причем, содержание ее будет зависеть от текущего состояния программы. Рассмотрим результаты моделирования стационарного температурного поля печатной платы с установленными на ней шестью ИС в керамических корпусах с числом выводов, равным 16 и 40 (рис. 3). Один край печатной платы, укрепленный в обойме теплового разъема, прижимается к каналу с протекающим
Рис. 4,
Рис. 5 внутри холодоносителем. С поверхностей платы и ИС происходит теплообмен со'средой. В качестве исходных данных задавались следующие параметры рассматриваемой конструкции: геометрические размеры платы и ее тепло проводность; геометрические размеры корпусов ИС, по требляемые ИС мощности, расположение ИС на плате, тепловые сопротивления ИС "переход-корпус" (RJ, количество выводов, теплопроводность материала выводов; размеры обоймы теплового разъема; температура среды; температура контакта обоймы теплового разъема и платы, которая получается на ос новании предварительного расчета теплового режима конструкции электронного устрой ства на третьем иерархическом уровне [2], Контакт теплового разъема и печатной платы разбивали на 24 площадки, по 12 с каждой стороны платы. Результаты моделирования приведены на рисунках 4,5. На рисунке 4 показаны изотермы на плате, на рисунке 5 — распределения температуры в сечениях платы А-А и В-В. Максимумы температуры расположены в центрах источников теплоты, минимумы - на торцах платы. Для сечения А-А минимальная температура составляет 18.5°С, что обусловливается отводом части теплового потока через тепловой разъем и жидкостный канал. Температуры корпусов для ИС с номерами 1-6 составляют (°С): 53.0, 54.5, 50.0, 62.2, 50.0, 63.0, а температуры кристаллов ИС составляют (°С): 85.0, 82.0, 104.2, 82.0, 105.0 соответственно. Как и следовало ожидать, максимальные температуры корпуса и кристалла имеют четвертая и шестая ИС, как наиболее мощные. Список литературы
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1453 |
Версия для печати |
| Статья опубликована в выпуске журнала № 3 за 1992 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- К вопросу об информатизации
- Проблемы визуализации и отображения информации
- Построение тестов для базовых функций встраиваемых операционных систем
- Сопряжение пакетов программ общего назначения с задачами жесткого реального времени
Назад, к списку статей