Развитие информационно-коммуникационных технологий и программных средств способствует повышению интеллектуального уровня систем исследования и управления технологическими процессами, разработке все более эффективных и совершенных интеллектуальных систем, входящих в информационные системы управления этими процессами. Такие системы особенно эффективны при управлении технологическими процессами, в которых решение о режимах управления принимается на основе обработки экспериментальных данных аналитическими приборами, не включенными в непрерывную цепь передачи и обработки информации и позволяющими получать набор количественных показателей процесса путем обработки малых количеств проб технологических материалов. В этом случае лицо, принимающее решение о режимах управления, обычно руководствуется некоторым графическим отображением одного или нескольких основных показателей процесса. Эф- фективность таких систем может быть значительно повышена, если для принятия управленческих решений будут использоваться математические модели, вычисляемые параметры которых однозначно описывают управляющие технологические показатели. Рассмотрим в качестве примера построение интеллектуальной системы поддержки управленческих решений при исследовании и управлении сложными химико-технологическими процессами структурирования многокомпонентных эластомерных композитов [1, 2].
На производстве изделий из многокомпонентных эластомерных композитов для определения основных показателей сложных химико-технологических процессов смешения и структурирования эластомерных систем широко применяются методы экспресс-контроля. Для количественного описания этих процессов используют аналитические приборы, позволяющие рассчитывать набор этих показателей процесса путем анализа и обра- ботки проб в малых количествах и на этой основе принимать оперативные решения по корректировке процесса.
В качестве основной информации, характеризующей эти процессы, используются данные виб- рореометрических испытаний, получаемые в ходе испытаний на реометрах различных конфигураций [2, 3].
Реограмма состояния представляет собой зависимость энергии, затрачиваемой на создание деформации сдвига в образце, от продолжительности вулканизации и количественно характеризует отклик материала на сдвиговые деформации.
Реометрическая кривая, вычерчиваемая реометром, является графическим отображением процесса структурирования эластомерного композита. Для проведения подобных испытаний применяют вибреометры различных конфигураций. Наиболее распространены приборы типа Монсанто [2]. После снятия кривой оператор-технолог рассчитывает основные характеристики процесса: время начала структурирования τs, время превращения на 10 % τ10, оптимальное время структурирования τ90, показатель скорости процесса Rv.
 Одним из наиболее современных вариантов та- кого прибора является прибор для испытания кау- чуков, резиновых смесей и резин, «Анализатор пе- рерабатываемости резин», RPA-2000 фирмы Alpha Technologies [4]. С использованием одного и того же образца на этом приборе можно получать данные о всех стадиях переработки каучуков (включая исходный полимер, резиновую смесь, ее свойства в процессе структурирования) и свойства вулканизованного продукта. Прибор соединен с персональным компьютером, что в отличие от виброреометра Монсанто дает возможность получать реографические данные сразу в цифровом виде. В качестве связующего ПО используется программа Enterprise Workbench 2k, позволяющая создавать различные программы испытаний образцов, изменяя температуру испытательной камеры и рабочих поверхностей, продолжительность проведения испытаний, частоту и амплитуду деформации. Данные о всех проведенных испытаниях хранятся в центральной БД. В ходе испытаний в режиме реального времени выдается информация по данному образцу (рис. 1).
Одним из наиболее современных вариантов та- кого прибора является прибор для испытания кау- чуков, резиновых смесей и резин, «Анализатор пе- рерабатываемости резин», RPA-2000 фирмы Alpha Technologies [4]. С использованием одного и того же образца на этом приборе можно получать данные о всех стадиях переработки каучуков (включая исходный полимер, резиновую смесь, ее свойства в процессе структурирования) и свойства вулканизованного продукта. Прибор соединен с персональным компьютером, что в отличие от виброреометра Монсанто дает возможность получать реографические данные сразу в цифровом виде. В качестве связующего ПО используется программа Enterprise Workbench 2k, позволяющая создавать различные программы испытаний образцов, изменяя температуру испытательной камеры и рабочих поверхностей, продолжительность проведения испытаний, частоту и амплитуду деформации. Данные о всех проведенных испытаниях хранятся в центральной БД. В ходе испытаний в режиме реального времени выдается информация по данному образцу (рис. 1).
Программа также позволяет получать данные по величинам действительной и мнимой частей комплексного модуля (S’ и S”), тангенса угла механических потерь δ. Данные параметры не только дают представление о свойствах сырой резиновой смеси – полуфабриката, но и характеризуют свой- ства готового изделия – продукции из эластомерных композитов [4–6].
Данные виброреометрических испытаний являются решающими для принятия решений по оперативному контролю и управлению сложными химико-технологическими процессами структурирования многокомпонентных эластомерных композитов [1–3].
 На основе информационно-логического анализа [1, 3, 7] технологических процессов смешения и структурирования эластомерных композитов было построено информационное обеспечение системы управления химико-технологическими процессами смешения и структурирования многокомпонентных эластомерных композитов. Архитектура данной системы приведена на рисунке 2.
На основе информационно-логического анализа [1, 3, 7] технологических процессов смешения и структурирования эластомерных композитов было построено информационное обеспечение системы управления химико-технологическими процессами смешения и структурирования многокомпонентных эластомерных композитов. Архитектура данной системы приведена на рисунке 2.
Система содержит ряд подсистем, в число которых, кроме подсистемы поддержки управленческих решений, входят подсистемы работы с документами.
Так, подсистема нормативной документации содержит информацию о нормативных характеристиках эластомерных композитов и показателях химико-технологических процессов их переработки.
Подсистема документов для ЛПР содержит формы основных отчетных документов по испытаниям эластомерных композитов и перечень получателей данной информации [1].
Подсистема поддержки принятия управленческих решений содержит блок визуализации реограмм состояния, БД реограмм, блок моделей и блок подготовки управленческих решений на основе продукционных моделей.
Так как основные параметры процесса структурирования не могут быть измерены непосредственно, в настоящее время управление процессами структурирования осуществляется с визуальным использованием данных реограмм состояния многокомпонентных эластомерных композитов. Так как на практике графические характеристики процесса для реальных систем сильно расходятся, для повышения эффективности управления процессом на основе анализа реограмм в работе пред- ложено использовать математические модели рео- грамм, которые были получены путем обработки более двухсот стандартных реограмм состояния [8]. Это позволило дополнительно исполь- зовать для описания процесса такие новые ко- личественные характеристики, как скорость структурирования  , ускорение процесса
, ускорение процесса  , обобщенное ускорение
, обобщенное ускорение  , время превращения на 50 % τ50, амплитуда А и мода Мо–с.
, время превращения на 50 % τ50, амплитуда А и мода Мо–с.
Новые показатели процесса позволяют использовать большее количество точек на реограмме, по которым осуществляются контроль и управление процессом. Это, в свою очередь, дает технологу дополнительные возможности при управлении режи- мами структурирования при получении изделий из эластомерных композитов [8–12].
Полученные в ходе испытаний на реометре Монсанто и приборе-анализаторе перерабатывае- мости резин RPA-2000 экспериментальные данные были использованы для аппроксимации реограмм состояния в программе Table Curve 2D. Программа автоматически рассчитывает уравнения различ- ного порядка сложности. В ранее проведенных работах показано, что для математической интерпретации реограмм состояния наиболее целесообразно использовать нелинейную пятипараметрическую модель из каталога программы [9–11, 13].
Модель имеет вид
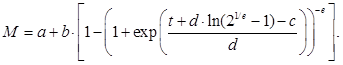 (1)
(1)
Здесь параметр a с учетом воспроизводимости реограмм состояния можно рассматривать как минимальный крутящий момент Mmin. Параметр b соответствует приращению крутящего момента ΔM = Mmax – Mmin. Параметр с равен вулканизационной характеристике tC(50). Параметры d и e связаны между собой и с вулканизационными характеристиками [11].
После нормировки β = (M – Mmin)/(Mmax – Mmin) имеем:
 (2)
(2)
Введение безразмерной величины β, характеризующей степень завершенности процесса, позволяет снизить влияние неконтролируемых переменных и практически совместить несколько кривых в одну [6, 9, 12, 13].
 На практике для описания процесса структурирования, помимо самих реограмм, представленных на рисунке 3а (интегральных кривых), целесообразно использовать также дифференциальные кри- вые скорости (дериватограммы) и ускорения, так как они оказываются более чувствительными при варьировании рецептурно-технологических факто- ров процесса [6]. Скорость вулканизации и ускоре- ние процесса, соответственно, выглядят следующим образом:
На практике для описания процесса структурирования, помимо самих реограмм, представленных на рисунке 3а (интегральных кривых), целесообразно использовать также дифференциальные кри- вые скорости (дериватограммы) и ускорения, так как они оказываются более чувствительными при варьировании рецептурно-технологических факто- ров процесса [6]. Скорость вулканизации и ускоре- ние процесса, соответственно, выглядят следующим образом:
 , (3)
, (3)
 (4)
(4)
Программа Table Curve 3d позволяет строить пространственные изображения для поверхностей отклика произвольной физической природы и аппроксимировать их математическими моделями различного уровня сложности. Представляет определенный интерес построение трехмерных изображений для зависимостей основных характеристик процесса структурирования от параметров выбранной модели и рецептурно-технологических факторов [9, 11]. Для описания подобных зависимостей использованы полиномиальные модели из каталогов программы Table Curve 3d. Эти полиномиальные зависимости имеют следующий вид:
Z = a + bx + cy + dx2 + ey2 + fxy, (5)
Z = a + bx + cy + dx2 + ey2 + fxy +
+ gx3 + hy3 + ixy2 + jx2y. (6)
Подобные модели позволяют количественно охарактеризовать влияние двух и более факторов на процесс структурирования эластомерных композитов.
 В качестве примера на рисунке 4 представлена поверхность отклика для скорости процесса.
В качестве примера на рисунке 4 представлена поверхность отклика для скорости процесса.
Аналогично можно построить поверхности отклика для крутящего момента при варьировании таких рецептурно-технологических факторов, как содержание ускорителя и время протекания процесса.
Для модели, представленной формулой (5), получены оценки погрешности: коэффициент детерминации – 0,91704; скорректированный коэффициент детерминации – 0,89861; стандартная ошибка – 3,8532; критерий Фишера – 61,9065. Аналогичные оценки погрешностей на основе критерия Фишера получены и для остальных моделей (уравнения (1) и (6)).
Для технолога представляется интересным получить графические решения в виде контурных графиков для оперативного контроля и управления процессами структрирования на основе анализа реографической информации [5, 6, 10, 11]. После подстановки выражения для нормировки получаем следующие дифференциальные уравнения, характеризующие зависимость скорости и ускорения процесса структурирования эластомерной системы от параметров модели е и d:
 (7)
(7)
 (8)
(8)
C учетом подстановок выражения для амплитуды и моды:
A·d = (e/(e + 1))e+1;
A =(e/(e + 1)e+1)/d; (9)
(Mo – c)/d = –ln(e·(21/e – 1)). (10)
Программный продукт MATLAB 7 позволяет строить семейство изолиний (контурных графиков). Для полученных трехмерных моделей приведены сечения, которые дают возможность охарактеризовать взаимодействие между параметрами модели. Далее представлен пример листинга для построения контурного графика с использованием команды contour:
>> [x, y] = meshgrid(0:1.2/60:1.2, 0:1.2/60:1.2);
b = 0.1;
z = (x./y).*(1 – b).*(1 – (1–b).^(1./y));
p = [0.05, 0.1, 0.15, …, 0.4]';
contour(x, y, z, p)
grid on
 Пример построения семейства изолиний для ускорения процесса структурирования
Пример построения семейства изолиний для ускорения процесса структурирования  от параметров модели d и e приведен на рисунке 5.
от параметров модели d и e приведен на рисунке 5.
Заключение
В работе показано, что задачи управления в процессах структурирования эластомерных композитов можно решать с помощью нескольких подходов: анализ реограмм состояния; выбор на основе анализа реографической информации точек управления и использование определенного набора количественных характеристик, каждая из которых не может быть непосредственно измерена, а получается путем отбора промежуточных проб и их испытаний на виброреометрическом приборе [2, 3]. Создание интегрированной интеллектуальной информационной системы управления и введение новых количественных показателей процесса путем построения моделей реограмм состояния позволяют увеличить число точек для более тонкого управления процессом и облегчить принятие реше- ний на производстве продукции из эластомерных композитов. Это, в свою очередь, дает возможность интенсифицировать производственные процессы смешения и структурирования многокомпонентных эластомерных композитов, повысить их энергоэффективность, а также снизить брак.
Таким образом, в статье предложены архитектура интегрированной интеллектуальной информационной системы управления сложными химико-технологическими процессами структурирования многокомпонентных эластомерных композитов, а также приемы рациональной математической интерпретации реограмм состояния эластомерных композитов с применением современных программных продуктов.
Представленные графические решения наглядно демонстрируют зависимости между основными характеристиками процесса структурирования эластомерных композитов и параметрами используемой математической модели.
На основе анализа экспериментальных данных процесса структурирования установлены пределы изменения параметров модели d и e.
Показана возможность использования новых количественных характеристик процесса структурирования, таких как скорости процесса струк- турирования  , амплитуды А, моды Mo–c, ускорения
, амплитуды А, моды Mo–c, ускорения  и обобщенного ускорения
и обобщенного ускорения  .
.
Предложены модели, позволяющие количественно охарактеризовать влияние нескольких факторов на процесс структурирования эластомерных композитов.
Разработанные подходы целесообразно использовать при анализе и контролировании процессов структурирования эластомерных композитов.
Литература
1. Бурляева Е.В., Колыбанов К.Ю., Панова С.А. Информационная поддержка систем принятия решений на производственных предприятиях химического профиля; [под науч. ред. В.Ф. Корнюшко]. М.: Изд-во МИТХТ, 2013. 195 с.
2. Новаков И.А., Вольфсон С.И., Новопольцева О.М., Кракшин М.А. Реологические и вулканизационные свойства эластомерных композиций. М.: Академкнига, 2008. 332 с.
3. Кузнецов А.С., Агаянц И.М., Корнюшко В.Ф. Реограмма как инструмент управления технологическим процессом структурирования эластомерных систем // Наукоемкие химические технологии-2015: сб. тр. науч.-практич. конф. М.: Изд-во МИТХТ, 2015. С. 143.
4. Monsanto Rheometer 100, Description and application. Technical Bulletin, no. IS-1, p. 18.
5. RPA 2000 – Dynamic Mechanical Rheological Tester. URL: http://www.alpha-technologies.com/products/rpa-2000 (дата обращения: 30.05.2017).
6. Monsanto Accelerator Rheographs, Brussels, 1987; Measuring visco-elastic properties using the MDR 2000 rheometer, Louvain-la-neuve, 1989, 20 p.
7. Кузнецов А.С., Корнюшко В.Ф., Гончаров И.А., Ага- янц И.М. Информационная поддержка системы управления технологическим процессом структурирования эластомерных систем с применением реометрических кривых // Прикладная информатика. 2016. № 1. С. 5–12.
8. Агаянц И.М., Наумова Ю.А., Кузнецов А.С. Анализ корреляционных соотношений в области реометрических исследований резин // Вестн. МИТХТ. 2013. Т. 8. № 1. С. 15–19.
9. Агаянц И.М. Натуральный каучук, в поисках рецепта. М.: Петергоф, 2010. 701 с.
10. Кашкинова Ю.В. Количественная интерпретация кинетических кривых процесса вулканизации в системе организации рабочего места технолога-резинщика: автореф. дис. … канд. технич. наук. М., 2005. 24 с.
11. Агаянц И.М. Азы статистики в мире химии. М.: Изд-во МИТХТ, 2012. 441 с.
12. Агаянц И.М., Кузнецов А.С., Овсяников Н.Я. Модификация осей координат при количественной интерпретации реометрических кривых // Тонкие химические технологии. 2015. № 2. С. 67–70.
13. Агаянц И.М., Кузнецов А.С., Корнюшко В.Ф. Модификация осей координат при количественной интерпретации реометрических кривых. Ч. II. Анализ взаимосвязей параметров моделей и вулканизационных характеристик // Междунар. науч.-исслед. журнал. 2016. № 5. С. 18–23.
14. Вoльфсон С.Л., Горелик В.М., Кучерский А.М. Определение модуля сдвига эластомеров на вулкаметрах с биконическим ротором // Каучук и резина. 1977. № 6. С. 57–59.
15. Корнюшко В.Ф., Костров А.В., Породникова П.А. Подход к развитию системы управления тестированием програм- мных средств // Программные продукты и системы. 2015. № 4. С. 126–132.
16. Корнюшко В.Ф., Бурляева Е.В., Колыбанов К.Ю., Арбенин Д.Е. Применение информационных технологий при многоуровневой подготовке специалистов химико-технологического профиля // Программные продукты и системы. 2009. № 4. С. 107–110.
17. Агаянц И.М. Азы статистики в мире химии: обработка экспериментальных данных. СПб: Изд-во НОТ, 2015. 614 с.
18. Гартман Т.Н., Клушин Д.В. Основы компьютерного моделирования химико-технологических процессов. М.: Академкнига, 2006. 416 с
19. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении. М.: Финансы и статистика, 2002. 368 с.
20. Дворецкий Д.С., Пешкова Е.В. Математическое моделирование и оптимизация процессов тонкого органического синтеза в условиях неопределенности // Вестн. ТГТУ. 2007. № 1. С. 119–129.
21. Мамбетова Е.А., Труфанова Н.М. Математическое моделирование температурных полей и степени вулканизации в процессе вулканизации типичных кабельных изделий // Вестн. ПНИПУ: Электротехника, информационные технологии, системы управления. 2012. № 6. С. 152–158.
22. Колодежнов В.Н., Березнев О.Г. Математическое моделирование и анализ поведения неньютоновских жидкостей с пределом применимости степенного закона вязкости // Вестн. ВГТУ. 2011. № 4. С. 197–200.
23. Тихомиров С.Г., Карманова О.В., Пятаков Ю.В., Маслов А.А. Программный комплекс для решения задач математического моделирования процесса изотермической вулканизации // Вестн. ВГУИТ. 2016. № 3. С. 93–99.
24. Осипов С.Ю., Осипов Ю.Р., Богданов Д.А., Ершов Е.В. Математическое моделирование и разработка системы автоматической корректировки режимов вулканизации эластомерных покрытий валов металлургических производств // Вестн. Череповец. гос. ун-та. 2017. № 3. С. 46–54.
25. Столбов Л.А., Дубавов Д.С., Филоретова О.А., Лиси- ца А.В. Системы информационного обеспечения при создании проблемно-ориентированной базы данных с применением когнитивного моделирования // Интеграл. 2013. № 1. С. 52–53.
References
- Burlyaeva E.V., Kolybanov K.Yu., Panova S.A. Informatsionnaya podderzhka sistem prinyatiya resheny na proizvodstvennykh predpriyatiyakh khimicheskogo profilya [Information Support of Decision-Making Systems at Chemical Industrial Enterprises]. V.F. Kornyushko (Ed.). Moscow, MITKhT Publ., 2013, 195 p.
- Novakov I.A., Volfson S.I., Novopoltseva O.M., Krakshin M.A. Reologicheskie i vulkanizatsionnye svoystva elastomernykh kompozitsy [Rheological and Vulcanization Properties of Elastomeric Compositions]. Moscow, IKTs Akademkniga Publ., 2008, 332 p.
- Kuznetsov A.S., Agayants I.M., Kornyushko V.F. A rheogram as a tool for managing the technological process of structuring elastomeric systems. Proc. Sci. and Pract. Conf. High-Tech Chemical Technologies. Moscow, MITKhT Publ., 2015, p. 143 (in Russ.).
- Monsanto Rheometer 100, Description and application. Technical Bulletin No IS-1, p. 18.
- Premier™ RPA. Rubber Process Analyzer. Available at: http://www.alpha-technologies.com/products/rpa-2000 (accessed May 30, 2017).
- Monsanto Accelerator Rheographs. Brussels, 1987; Measuring visco-elastic properties using the MDR 2000 rheometer, Louvain-la-neuve, 1989, 20 p.
- Kuznetsov A.S., Kornyushko V.F., Goncharov I.A., Agayants I.M. Information support of process structuring elastomeric systems control system using the rheometer curves. Prikladnaya informatika [Jour. of Applied Informatics]. 2016,
no. 2 (62), pp. 5–12 (in Russ.).
- Agayants I.M., Naumova Yu.A., Kuznetsov A.S. Analysis of correlation relationships in rheometric studies of rubbers. Vestnik MITKhT [Bulletin of MIREA]. 2013, vol. 8, no. 1, pp. 15–19 (in Russ.).
- Agayants I.M. Naturalny kauchuk, v poiskakh retsepta [Natural Rubber, in Search of a Recipe]. Moscow, PTs. Petergof Publ., 2010, 701 p.
- Kashkinova Yu.V. Kolichestvennaya interpretatsiya kineticheskikh krivykh protsessa vulkanizatsii v sisteme organizatsii rabochego mesta tekhnologa-rezinshchika [Quantitative Interpretation of Kinetic Curves of a Vulcanization Process in the System of Rubber Technologist Workplace Organization]. Ph.D. Thesis. Moscow, 2005, 24 p.
- Agayants I.M. Azy statistiki v mire khimii [The Basics of Statistics in the World of Chemistry]. Moscow, MITKhT Publ., 2012, 441 p.
- Agayants I.M., Kuznetsov A.S., Kuznetsov A.S., Ovsyanikov N.Ya. Modification of axes in rheometer curves quantitative interpretation. Tonkie khimicheskie tekhnologii [Fine Chemical Technologies]. 2015, no. 2, pp. 67–70 (in Russ.).
- Agayants I.M., Kuznetsov A.S., Kuznetsov A.S., Kornyushko V.F. Modification axes in rheometer curves quantitative interpretation. Report II. The relationship of parameters of the model and cure characteristics analysis. Mezhdunar. nauch.-issledovatelsky zhurnal [Int. Research Jour.]. 2016, no. 5 (47), pp. 18–23 (in Russ.).
- Volfson S.L, Gorelik V.M., Kuchersky A.M. Determination of a elastomer shear modulus on volcameters with a biconical rotor. Kauchuk i rezina [Rubber]. 1977, no. 6, pp. 57–59 (in Russ.).
- Kornyushko V.F., Kostrov A.V., Porodnikova P.A. An approach to software testing management system development. Programmnye produkty i sistemy [Software & Systems]. 2015, no. 4, pp. 126–132 (in Russ.).
- Kornyushko V.F., Burlyaeva E.V., Kolybanov K.Yu., Arbenin D.E. Application of information technologies for multilevel training of chemical-technological specialists. Programmnye produkty i sistemy [Software & Systems]. 2009, no. 4,
pp. 107–110 (in Russ.).
- Agayants I.M. Azy statistiki v mire khimii: obrabotka eksperimentalnykh dannykh [The Basics of Statistics in the World of Chemistry: Processing of Experimental Data]. St. Petersburg, NOT Publ., 2015, 614 p.
- Gartman T.N., Klushin D.V. Osnovy kompyuternogo modelirovaniya khimiko-tekhnologicheskikh protsessov [Basics of Computer Modeling of Chemical and Technological Processes]. Moscow, Akademkniga Publ., 2006, 416 p.
- Anfilatov V.S., Emelyanov A.A., Kukushkin A.A. Sistemny analiz v upravlenii [System Analysis in Management]. Moscow, Finansy i statistika Publ., 2002, 368 p.
- Dvoretsky D.S., Peshkova E.V. Mathematic Modeling and optimization of the processes of fine organic synthesis in terms of uncertainty. Vestnik TGTU [Trans. of TSTU]. 2007, no. 1, pp. 119–129 (in Russ.).
- Mambetova E.A., Trufanova N.M. Mathematical modeling of temperature fields and degrees of vulcanization during vulcanization of typical cable products. Vestn. PNIPU: Elektrotekhnika, informatsionnye tekhnologii, sistemy upravleniya [PNRPU Bulletin. Electrotechnics, Informational Technologies, Control Systems]. 2012, no. 6, pp. 152–158 (in Russ.).
- Kolodezhnov V.N., Bereznev O.G. Mathematical modeling and analysis of the behavior of non-Newtonian liquids with the applicability limit of the viscosity power law. Vestn. VGTU [The Bulletin of VSTU]. 2011, no. 4, pp. 197–200 (in Russ.).
- Tikhomirov S.G., Karmanova O.V., Pyatakov Y.V., Maslov A.A. The software package for solving problems of mathematical modeling of isothermal curing process. Vestn. VGUIT [Proc. of the Voronezh State University of Engineering Technologies]. 2016, no. 3, pp. 93–99 (in Russ.).
- Osipov S.Yu., Osipov Yu.R., Bogdanov D.A., Ershov E.V. Mathematical modeling and development of automatic correction system for vulcanization regimes of elastomeric coatings for shafts of metallurgical industries. Vestn. Cherepovets. gos. un-ta [Cherepovets State Univ. Bulletin]. 2017, no. 3, pp. 46–54 (in Russ.).
- Stolbov L.A., Dubavov D.S., Filoretova O.A., Lisitsa A.V. Information support systems when creating a problem-oriented database using cognitive modeling. Integral [Integral]. 2013, no. 1, pp. 52–53 (in Russ.).





 , ускорение процесса
, ускорение процесса  , обобщенное ускорение
, обобщенное ускорение  , время превращения на 50 % τ50, амплитуда А и мода Мо–с.
, время превращения на 50 % τ50, амплитуда А и мода Мо–с.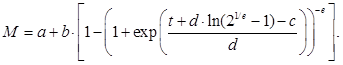 (1)
(1) (2)
(2)
 , (3)
, (3) (4)
(4)
 (7)
(7) (8)
(8)
 .
.