Программные продукты и системы

При проектировании компьютерных систем различного прикладного назначения должны достигаться высокая устойчивость и безопасность функционирования в условиях отказов и деструктивных случайных или злонамеренных воздействий [1–3].

Функциональная надежность и безопасность компьютерных систем определяются организацией как процесса передачи данных и распределения запросов через сеть, так и вычислительных процессов в серверах, объединяемых в дублированные отказоустойчивые комплексы [4, 5]. Надежность дублированных серверных систем обеспечивается выбором их дисциплин контроля, реконфигурации и вос- становления после отказов [6, 7]. Высокая го- товность системы обработки данных к безопасному функционированию может поддерживаться объединением серверных систем (в том числе дублированных) в отказоустойчивые кластеры при динамическом распределении запросов с учетом накопления отказов в систе- ме [8, 9].

При неоднородности потока запросов дополнительные возможности обеспечения своевременности решения требуемых задач дает динамическая приоритезация обслуживания запросов [10–12], осуществляемая на уровне кластера, дублированных вычислительных комплексов и их компьютерных узлов. Повы- сить доступность (готовность) серверных ресурсов удается на уровне сети при резервировании сетевых ресурсов и динамической, в том числе многопутевой, маршрутизации [13–15].

Контроль дублированных комплексов должен быть организован так, чтобы при обеспечении высокой безопасности, готовности и надежности системы минимизировать задержки обслуживания функциональных запросов. Таким образом, выбор организации контроля должен базироваться на постановке и решении оптимизационной задачи [16, 17].

Эффективность обнаружения нарушений функционирования определяется полнотой оперативного и периодичностью тестового контроля [5, 18]. Уменьшение интервалов периодичности контроля приводит к снижению готовности системы из-за роста временных издержек на тестирование, но в то же время повышает ее безопасность в результате снижения вероятности функционирования системы в состояниях необнаруженных отказов [16]. Увеличение полноты контроля приводит к усложнению структуры системы и, соответственно, к росту ее стоимости, веса, габаритов и потребляемой электроэнергии [19]. Для резервированных кластерных систем [8, 9] выбор наилучших вариантов организации контроля усложнен тем, что, помимо оптимизации интервалов тестирования каждого устройства, включает определение расписаний тестирования и числа машин, одновременное тестирование которых допустимо, в зависимости от критичности времени выполнения решаемых ими прикладных задач.

В качестве основы для построения распределенных отказоустойчивых систем, в том числе кластерной архитектуры, используются дублированные системы, объединяющие пару компьютерных узлов, снабженных средствами оперативного и тестового контроля. В системах с дублированием компьютерных узлов возможны режимы разделения нагрузки, когда узлы независимо выполняют разделяемый между ними поток запросов, и режим дублированных вычислений, когда каждый запрос одновременно выполняется двумя компьютерными узлами при сравнении результатов в контрольных точках.

В системе возможна неоднородность потока запросов, поступающих на дублированный компьютерный узел, при которой часть запросов требуют дублированных вычислений (с выдачей результатов только при их совпадении), а часть могут обслуживаться в режиме разделения нагрузки, в том числе одной из ма- шин в случае отказа или тестирования второй.

В зависимости от однородности входного потока выделим следующие ситуации: поток однороден, любой запрос выполняется на одном из компьютеров узла; поток однороден, любой запрос требует дублированного выполнения двумя компьютерами узла; поток неоднороден, при этом часть запросов требуют дублированного выполнения двумя компьютерами узла, а часть выполнимы на одном компьютере.

Для однородного потока запросов, не требующих дублирования вычислений, обслуживание которых происходит в режиме разделения нагрузки, одновременный тестовый контроль двух узлов нежелателен, так как может при- вести к снижению вероятности готовности системы [16]. Для входного потока, предусматривающего дублированное обслуживание запросов в двух машинах со сравнением результатов, готовность повышается при одновременном тестировании пары узлов, так как ресурсов только одного из узлов недостаточно для организации дублированного вычислительного процесса. Модель надежности дублированных систем при разделении нагрузки исследована в работе [16], в ней проанализированы варианты инициализации тестового контроля, при которых одновременное тестирование двух узлов исключено, допустимо и реализуется всегда.

В работе [16] обоснован выбор дисциплины контроля и определены оптимальные интервалы инициализации тестирования, обеспечивающие максимум вероятности готовности системы к безопасному функционированию в зависимости от характера потока запросов, требующих выполнения одним или двумя узлами одновременно. Показано существование оптимальных периодов инициализации тестирования для всех рассмотренных вариантов организации контроля, при которых достигается максимум вероятности готовности системы к безопасному выполнению требуемых функций.

Постановка задачи исследований

В предлагаемой статье для дублированных систем с разделением нагрузки исследуется потенциальная возможность повышения эффективности контроля в результате периодического перехода в режим дублированных вычислений со сравнением результатов, что позволяет уменьшить издержки на проведение тестового контроля (дублированной системы), инициируя его только в случае несовпадения результатов дублированных вычислений.

Цель работы – определение оптимальных интервалов перехода в режим дублированных вычислений для обеспечения максимума вероятности готовности системы к безопасному выполнению функциональных запросов при минимизации простоев и задержек обслуживания.

Для достижения поставленной цели необходимо:

-     построить модель, позволяющую определить вероятности состояний системы, в том числе состояний готовности системы к безопасному функционированию и опасных состояний функционирования системы в условиях необнаруженных отказов;

-     проанализировать влияние периодичности переходов в режим дублированных вычислений на достижимость максимума вероятности готовности системы к безопасному обслуживанию запросов при минимизации задержек их выполнения и простоев системы.

При определении оптимальных интервалов инициализации режима дублированных вычислений в качестве целевой функции можно рассматривать достижение максимума вероятности работоспособности двух машин при их нахождении в состоянии выполнения функциональных запросов в режиме разделения нагрузки, так как этот режим обеспечивает максимум производительности дублированной вычислительной системы при учете простоев и опасных состояний.

Для систем с меньшей критичностью производительности (задержек обслуживания функциональных запросов) в качестве целевой функции (критерий оптимальности) можно рассматривать достижение максимума вероятности K готовности системы к выполнению функциональных задач (стационарный коэффициент готовности системы), которая обеспечивается при работоспособности двух машин и их нахождении в состоянии готовности выполнения функциональных запросов в режиме разделения нагрузки или режиме дублированных вычислений, а также состояний исправности и готовности к выполнению требуемых функций одной из машин при условии безопасного состояния второй машины (состояния обнаруженного отказа).

Для систем с повышенными требованиями к безопасности целевую функцию можно задать в виде мультипликативной скалярной свертки M = K(1 – P0) или M = K/P0 , где P0 – вероятность опасного состояния необнаружен- ных отказов системы. При этом возможна модификация представленных сверток с учетом задания критичности системы к безопасному функционированию, например, как M = = K(1-a)(1 – P0)a , где через а задается степень критичности системы к требованиям безопасности (0 ≤ a ≤ 1). Следует заметить, что задание a = 1 равносильно минимизации вероятности нахождения системы в состояниях необнаруженных отказов, а это приведет к тому, что в качестве оптимального будет определен режим постоянного дублирования вычислений.

Вероятностные характеристики исследуемых дублированных систем определим на основе марковских моделей [18, 20], исследование которых эффективно при использовании инструментария компьютерной математи- ки [21].

Марковская модель надежности

При построении марковской модели будем учитывать возможность возникновения отказов во время режимов дублированных вычислений и тестирования, при этом предполагаем идеальность тестового контроля, заключающуюся в гарантированном выявлении им места неисправности системы.

Диаграмма состояний и переходов марковской модели дублированной компьютерной системы при реализации рассматриваемой дисциплины контроля и восстановления представлена на рисунке 1, где вершины отображают состояния устройств в системе. Состояние работоспособности устройства (машины) обозначено 1, обнаруженного и необнаруженного отказа – 0 и 0* соответственно. Состояния дублированных вычислений и тестирования обозначены D и T соответственно. На рисунке 1 все состояния пронумерованы в соответствии с их вероятностями: Р1, Р2, …, Р12. Исходное состояние Р1 соответствует готовности к функционированию двух машин, а состояния Р2, Р4, Р6 – готовности одного работоспособного устройства. Состояния Р7–Р9 соответствуют нахождению системы в режиме дублированных вычислений, а состояния Р10–Р12 – в режиме тестирования (при котором выполнение функциональных задач блокируется). К опасным состояниям функционирования в условиях необнаруженных отказов относятся состояния Р4, Р5, Р6. Через Р3 обозначено состояние обнаруженного отказа системы. Состояние Р7 дублированных вычислений при работоспо- собности двух машин позволяет системе выполнять функциональные задачи.

Вероятность нахождения системы в опасных состояниях необнаруженных отказов определяется как P0 = Р4+ Р5 + Р6.

По графу состояний и переходов составим систему уравнений Колмогорова:

где , ,

, ,

, ,

,

, ,

, ,

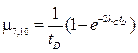, , где λ – интенсивность отказов; g – доля контролируемых отказов (средствами оперативного контроля); m – интенсивность восстановления; tD – время дублированных вычислений; tT – время тестирования; λC – интенсивность сбоев; λD – интенсивность переходов в режим дублированных вычислений.

Решение системы уравнений получено с использованием блока Given-Find системы компьютерной математики Mathcad 15.

Вероятность готовности (стационарный коэффициент готовности) системы к безопасному выполнению требуемых функций определим как К = Р1 + Р2 + Р7.

Пример расчетов

На рисунке 2 показана зависимость вероятности рабочего состояния системы от интен- сивности переходов в режим дублированных вычислений. Расчеты проведены при λ = 10-4 (1/ч), g = 0,5, m = 1 (1/ч), tD = 1/3600 (ч), tT = 1/3 (ч), λC = 10-3 (1/ч).

Результаты расчетов показывают существование оптимальной периодичности инициализации режима дублированных вычислений, при которой достигается максимум вероятности готовности системы к безопасному выполнению требуемых функций при минимизации простоев системы.

Таким образом, предложена марковская модель надежности дублированной вычислительной системы, позволяющая найти рациональные варианты организации контроля функционирования системы, направленного на обеспечение безопасности и надежности системы. Показано существование оптимальной периодичности перехода в режим дублированных вычислений, при которой достигается максимум вероятности готовности системы к безопасному выполнению требуемых функций при минимизации простоев системы.

Литература

1.    Казарин О.В., Шубинский И.Б. Надежность и безопасность программного обеспечения. М.: Юрайт, 2018. 342 с.

2.    Верзун Н.А., Колбанев М.О., Татарнико- ва Т.М. Технологическая платформа четвертой промышленной революции // Геополитика и безопасность. 2016. № 2. С. 73–78.

3.    Абрамян Г.В. Структура и функции информационной системы мониторинга и управления рисками развития малого и среднего бизнеса Северо-Западного федерального округа // Аудит и финансовый анализ. 2017. № 5–6. С. 611–617.

4.    Sorin D. Fault tolerant computer architecture. Morgan & Claypool Publ., 2009, 103 p.

5.    Половко А.М., Гуров С.В. Основы теории надежности. СПб: БХВ-Петербург, 2006. 702 с.

6.    Ageev A.M. Сonfiguring of excessive onboard equipment sets. J. Comput. Syst. Sci. Int. 2018, vol. 57, no. 4, pp. 640–654.

7.    Гатчин Ю.А., Видин Б.В., Жаринов И.О., Жаринов О.О. Модели и методы проектирования интегрированной модульной авионики // Вестн. компьтер. и информ. технол. 2010. № 1. С. 12–20.

8.    Богатырев В.А., Богатырев С.В. Надежность мультикластерных систем с перераспределением потоков запросов // Изв. вузов: Приборостроение. 2017. Т. 60. № 2. С. 171–177.

9.    Богатырев В.А., Богатырев А.В., Голу- бев И.Ю., Богатырев С.В. Оптимизация распределения запросов между кластерами отказоустойчивой вычислительной системы // Науч.-технич. вестн. ИТМО. 2013. № 3. С. 77–82.

10. Aliev T.I. The synthesis of service discipline in systems with limits. CCIS, 2016, vol. 601, pp. 151–156. DOI: 10.1007/978-3-319-30843-2_16.

11. Жмылёв С.А., Алиев Т.И. Системы массового обслуживания с полимодальными потоками // Науч.-технич. вестн. ИТМО. 2018. Т. 18. № 3. С. 473–478.

12. Алиев Т.И., Муравьева-Витковская Л.А. Приоритетные стратегии управления трафиком в мультисервисных компьютерных сетях // Изв. вузов: Приборостроение. 2011. Т. 54. № 6. С. 44–48.

13. Татарникова Т.М. Аналитико-статистическая модель оценки живучести сетей с топологией mesh // Информационно-управляющие системы. 2017. № 1. С. 17–22. DOI: https://doi.org/ 10.15217/issnl684-8853.2017.1.17.

14. Богатырев В.А., Богатырев С.В., Богатырев А.В. Оптимизация древовидной сети с резервированием коммутационных узлов и связей // Телекоммуникации. 2013. № 2. С. 42–48.

15. Шувалов В.П., Вараксина И.Ю. Классификация методов многопутевой маршрутизации // T-Comm: Телекоммуникации и Транспорт. № 1. 2014. С. 29–32.

16. Bogatyrev V.A., Vinokurova M.S. Control and safety of operation of duplicated computer systems. CCIS, 2017, vol. 700, pp. 331–342. DOI: 10.1007/978-3-319-66836-9_28.

17. Гришенцев А.Ю., Коробейников А.Г. Постановка задачи оптимизации распределенных вычислительных систем // Программные системы и вычислительные методы. 2013. № 4. С. 370–375.

18. Шубинский И.Б. Надежные отказоустойчивые информационные системы. Методы синтеза. Ульяновск: Печатный двор, 2016. 544 с.

19. Колбанёв М.О., Татарникова Т.М. Физиче- ские ресурсы информационных процессов и тех- нологий // Науч.-технич. вестн. ИТМО. 2014. № 6. С. 113–122.

20. Клейнрок Л. Теория массового обслуживания. М.: Машиностроение, 1979. 432 с.

21. Коробейников А.Г., Гришенцев А.Ю. Разработка и исследование многомерных математических моделей с использованием систем компьютерной алгебры. СПб: Изд-во НИУ ИТМО, 2014. 100 с.

References

1. Kazarin O.V., Shubinsky I.B. Reliability and Security of Software: Study Manual for Undergraduates and Graduates. Moscow, Yurauyt, 2018, 342 p.
2. Verzun N.A., Kolbanev M.O., Tatarnikova T.M. Technological platform of the fourth industrial revolution. Geopolitics and Security. 2016, no. 2, pp. 73–78 (in Russ.).
3. Abramyan G.V. The structure and functions of the information system for monitoring and managing the development risks of small and medium-sized businesses in the North-West Federal District. Audit and Financial Analysis. 2017, no. 5, pp. 611–617 (in Russ.).
4. Sorin D. Fault Tolerant Computer Architecture. Morgan & Claypool Publ., 2009, 103 p.
5. Polovko A.M., Gurov S.V. Fundamentals of the Theory of Reliability. St. Petersburg, BHV-Peterburg Publ., 2006, 702 p.
6. Ageev A.M. Configuring of excessive onboard equipment sets. J. of Computer and Systems Sciences Intern. 2018, vol. 57, no. 4, pp. 640–654 (in Russ.).
7. Gatchin Yu.A., Vidin B.V., Zharinov I.O., Zharinov O.O. Models and methods of integrated modular avionics designing. Herald of Computer and Information Technologies. 2010, no. 1, pp. 12–20 (in Russ.).
8. Bogatyrev V.A., Bogatyrev S.V. Reliability of multicluster systems with redistribution of request flows. J. of Instrument Engineering. 2017, vol. 60, no. 2, pp. 171–177 (in Russ.).
9. Bogatyrev V.A., Bogatyrev A.V., Golubev I.Yu., Bogatyrev S.V. Queries distribution optimization between clusters of fault-tolerant computing system. Scientific and Technical J. of Information Technologies, Mechanics and Optics. 2013, no. 3, pp. 77–82 (in Russ.).    
10. Aliev T.I. The synthesis of service discipline in systems with limits. Communications in Computer and Information Science. 2016, vol. 601, pp. 151–156. DOI: 10.1007/978-3-319-30843-2_16.
11. Zhmylev S.A., Aliev T.I. Queue systems with polymodal query flows. Scientific and Technical J. of Information Technologies, Mechanics and Optics. 2018, vol. 18, no. 3, pp. 473–478 (in Russ.).
12. Aliev T.I., Muravyeva-Vitkovskaya L.A. Priority-based strategies of traffic management in multiservice computer networks. J. of Instrument Engineering. 2011, vol. 54, no. 6, pp. 44–48 (in Russ.).
13. Tatarnikova T.M. Analytical-statistical model of mesh network survivability evaluation. Information and Control Systems. 2017, no. 1, pp. 17–22 (in Russ.). DOI: 10.15217/issnl684-8853.2017.1.17.
14. Bogatyrev V.A., Bogatyrev S.V., Bogatyrev A.V. Tree network optimization with redundant switching nodes and connections. Telecommunications. 2013, no. 2, pp. 42–48 (in Russ.).
15. Shuvalov V.P., Varaksina I.Yu. Classification of multi-path routing methods. T-Comm., 2014, no. 1,
    pp. 29–32 (in Russ.).
16. Bogatyrev V.A., Vinokurova M.S. Control and safety of operation of duplicated computer systems. Communications in Computer and Information Science. 2017, vol. 700, pp. 331–342. DOI: 10.1007/978-3-319-66836-9_28.
17. Grishentsev A.Yu., Korobeynikov A.G. Statement of the optimization problem of distributed computing systems. Software Systems and Computing Methods. 2013, no. 4, pp. 370–375 (in Russ.).
18. Shubinsky I.B. Reliable Fault-Tolerant Information Systems. Synthesis Methods. Ulyanovsk, Pechatny dvor Publ., 2016, 544 p.
19. Kolbanev M.O., Tatarnikova T.M. Physical resources of information processes and technologies. Scientific and Technical J. of Information Technologies, Mechanics and Optics. 2014, no. 6, pp. 113–122
    (in Russ.).
20. Kleynrok L. Queuing Theory.  Moscow, Mashinostroenie Publ., 1979, 432 p.
21. Korobeynikov A.G., Grishentsev A.Yu. Development and Research of Multidimensional Mathematical Models Using Computer Algebra Systems. St. Petersburg, NIU ITMO Publ., 2014, 100 p.