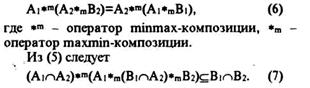Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Экологический мониторинг на предприятиях нефтеперераба ты бающей промышленности на основе методов и моделей искусственного интеллекта
Аннотация:
Abstract:
| Авторы: Минаев Ю.Н. () - , Тонкаль С.С. () - , Филимонова О.Ю. () - , Куклин В.Ю. () - , Мруе М.Л. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10878 |
Версия для печати |
Практика последних лет, когда промышленные предприятия, занимающие огромные площади и включающие большое число мощных источников выбросов вредных веществ, располагаются в относительной (или в абсолютной) близости от селитебных зон, требует нового подхода к экологическому мониторингу. Важной становится проблема оперативного определения источника выбросов, приводящего к превышению предельно допустимых концентраций в селитебных зонах, и соответствующей реакции - изменения технологии, снижения мощности или других управляющих воздействий. С целью оперативного мониторинга по периметру промзоны размещают стационарные или переносные посты наблюдения, в которых регистрируются концентрации вредных веществ. Существуют компьютерные методики определения или прогноза концентрации вредных веществ в точках поверхности с координатами (X,Y) в зависимости от мощности источника, его геометрических пространственных характеристик, удаления от точки анализа, метеоусловий, характеристик территории и др. В качестве примера можно привести программный комплекс "ZONE" [1]. Не касаясь особенностей этого комплекса, отметим, что решение одной из главных задач экологического мониторинга - определение основного источника выброса вредных веществ в промзоне, решаемое при помощи традиционных методов (гидромеханика и термогидродинамика) - не только требует весьма дорогостоящих измерений, например высотных, выполняемых при помощи летательных аппаратов, но и приводит к некорректной задаче. При экологическом мониторинге в настоящее время учитывают прежде всего экономическую целесообразность, то есть требуется подобрать такие способы его проведения, чтобы он был простым и сравнительно недорогим. Предприятие может пойти на внедрение мониторинга, если: - минимизировано количество натурных испытаний на промплощадке, например непосредственное определение интенсивности выбросов вредных веществ; - алгоритм (метод) должен давать возможность выполнять решение задач прогноза, например относительно уровня выбросов в селитебной зоне при работе того или иного производства; это позволит не включать конкретное производство при определенном направлении ветра и др. Исследования показали возможность решения задачи оперативного экологического мониторинга, в частности определения источника вредных выбросов на основе методов и моделей искусственного интеллекта, ситуационного моделирования [2,3,4]. Возможность такого подхода диктуется и такими соображениями. 1. Уровень вредных выбросов V в расчетных точках селитебных и промышленных зон полностью определяется условиями работы производства Пj (мощность, технологический режим, степень изношенности оборудования, использование природоохранных средств идр.), метеоусловиями М (температура и влажность воздуха, скорость и направление ветра), а также географическими особенностями промышленной Gп и селитебной зон Gs (высота источников выбросов, рельеф местности, этажность застройки и др.). Практически всегда могут быть определены ситуации в виде утверждений <если А, то В> или <если (П1, Gп, Gs), то V1>. Эксперт - технолог предприятия - в большинстве случаев может дать удовлетворительный ответ на вопрос: каковы будут примерные уровни вредных выбросов на границе промышленной и селитебной зон, если работает технологическая линия N__ на мощность , технологический режим , плановый ремонт оборудования не выполнен, ветер северо-западный, умеренный до сильного, прохладно? 2. Практика и жизненный опыт показывают, что между множествами {П,M,G} и {V}существуют скрытые закономерности, которые целесообразно использовать. В [1] показана рациональность использования допущения о стабильности законов распределения и гауссовой модели факелов. Гипотезу стабильности можно расширить и полагать стабильной (естественно, в пределах определенного времени) ситуацию, описывающуюся причинно-следственною моделью <если А, то В>. 3. При построении программного комплекса, реализующего оперативный экологический мониторинг, необходимо использовать принцип обучения (самообучения) и отказаться от многократного использования всевозможных поправочных коэффициентов. 4. Следует отметить то обстоятельство, что практически все расчетные параметры определяются весьма приблизительно, что исключает возможность применения точных методов. Таким образом, решение поставленной задачи целесообразно выполнять с учетом того, что она является недостаточно формализованной и содержит: а) параметры, учитываемые в виде нечетких утверждений; б) параметры, задаваемые неточно. Мощность (или объем) выбросов связана с мощностью работы установки или другими параметрами, характеризующими ее работу нечеткими высказываниями типа "если установка работает примерно на полную мощность или имеет место грубое нарушение технологии, или подано плохо подготовленное сырье, или не проведен планово-предупредительный ремонт оборудования, то объем выбросов максимальный". Как показывает практика, все ситуации, связанные с увеличением вредных выбросов прямо связаны с мощностью, потребляемой установкой или расходом энергоносителя, например электроэнергии. При этом нередки ситуации, когда небольшое увеличение расхода электроэнергии по сравнению с проектным свидетельствует о значительном увеличении выбросов. К сожалению, в проектной документации, как правило, отсутствуют сведения о связи выбросов с расходом энергоносителей. Это предмет отдельного исследования. В [6] показано, что нечеткое утверждение <если А, то В> может рассматриваться как общее выражение системы, допускающей альтернативное представление, то есть неоднозначность. В [2,3,6] предложено множества А и В, рассматривать как "вход-выход" (в общем случае неоднозначный), отождествляя с множествами {А} и {В}, в частности, матрицу отношений [R] (в дальнейшем матричное отношение), которое определяется моделью системы. Это позволяет получать условно однозначную связь не между отдельными элементами множеств, а между самими множествами. В [9,10] показано, что если отношения "вход-выход" заданы, то модель системы можно сформулировать с помощью правил композиционного вывода. Системное уравнение определяется выражением Bj=Aj*[R], где Aj,Bj -входное и выходное множества (индекс j может означать номер испытания); * - некоторый оператор, R - матрица отношения.
Предположим, что А={ai/fia}, Для построения алгоритма используется выражение
B={bj/fjb},
Показано [6], что недостаточно формализованную систему, характеризуемую матрицей [R], задаваемую утверждением А=>В, можно определить из условия
На основе совокупности утверждений (3) необходимо определить матрицу R и операцию * таким образом, чтобы: а) для всех заданных пар (Ai, Bi) Bi=Ai*[R]("i);Построение интегрального отношения [R] для всей совокупности (3) выполняют следующим образом [6,8]. Пусть для одной пары б) для входных множеств A'i и A"i за исключением данного входного множества; (А°,В°) получены отношение R0 и дополнительная информация A1=>B1. В этом случае представление системы R, содержащей R° и A1 =>B1, имеет вид: Если имеются две пары “вхвод-выход” и А2=>В2, которые не противоречат друг другу, то они с учетом (5) могут быть соответственно представлены: Из приведенных соотношений следует, что представленные системы эквивалентно представлению матрицы R в виде реализации maxmin-оператора
где R определено на всех парах Aj=>Bj, j=l,n из соотношения (1), и выполняется условие непротиворечивости (7). С учетом полученных результатов рассмотрим конкретный пример применения предложенной методики к решению задач автоматизации процедур определения источника загрязнения или его "вклада" в состояние воздушного бассейна. Отметим, что понятия "вход-выход" в значительной мере условны и не всегда могут совпадать с их физической трактовкой. Например, с физической точки зрения причина (вход) - источники выбросов и метеоусловия, следствие (выход) - уровни концентраций. Но с формальной точки зрения такая постановка не обязательна, математически входом можно считать измеренные величины, выходом - прогнозируемые, определяемые из соотношения A=B*R. Показано [9, 12], что в общем случае модель <если А, то В> можно рассматривать в виде F А=>В, где F - условия, при которых реализована пара (АÞВ). Справедливо соотношение AÞBÈF или AÇFÞB. Сделаем следующие выводы: 1.Для решения задач оперативного экологического мониторинга, в частности определения источника вредных выбросов, целесообразно применение методов и моделей искусственного интеллекта. 2. Нечеткое утверждение <если А, то В> может рассматриваться как общее выражение системы, допускающей альтернативное представление. Множества А и В предложено рассматривать соответственно как входы и выходы системы (источники выбросов Þ уровни концентраций вредных веществ в заданных точках) и определять условно-однозначную связь не между отдельными элементами множеств, а между самими множествами. 3. Определено системное уравнение вида A=B*[R], где А и В - выходное и входное множества соответственно, * - оператор max min-(min max)-композиции, на основании которого выполняется решение основных задач мониторинга.
Пример организации диалога Введите количество пар множеств А и В:2 число элементов множества А:3 число элементов множества В :10 Обучающая последовательность Bi={b1j} j=l,10; A1={a1i}, i=l,3 Функции принадлежности 1-го выхода Производство №1:=0.6; Производство №2:-=0,3; Производство №3:=0.8; Цех №4:=0.4; Цех №5:=0.3; Цех №6:=0.5; Цех КИП:=1; Цех №9:=0.7; Цех №13:=0; Цех №14:=0.9. Функции принадлежности 1-го входа Углеводороды предельные :=0; Углеводороды непредельные :=0.4; Сероводороды :=0.8. B2={b2j} j=l,10; A2={a2i},i=l,3 Функции принадлежности 2-го выхода Производство №1:=0.1; Производство №2: =0.9; Производство №3:=0.3; Цех №4:=0.4; Цех №5:=0.5; Цех №6:=0.2; Цех КИП:=0.1; Цех №9:=0.5; Цех №13:=0.2; Цех №14:=0.1 Функции принадлежности 2-го входа Углеводороды предельные :=0.3; Углеводороды непредельные :=0.6; Сероводороды :=0.9. Контрольная последовательность A0={aii0}, Углеводороды предельные :=0.9; Углеводороды непредельные :=0.5; Сероводороды :=0.3. Применяя A0 *R, получаем:Bo=Ao*RЦех КИП = 0.100 Производство №1 = 0.100Цех №9 = 0.900 Производство №2 = 0.900 Цех №13 = 0.200 Производство №3 = 0.900Цех №14 = 0.100 Цех №4 = 0.900Цех №5 = 0.900 Цех №6 = 0.200 Дальнейшая работа системы поясняется приводимым иллюстративным примером. На рисунке приведена общая схема расположения постов наблюдения и источников выбросов в конкретных заводских координатах и указаны контролируемые ингредиенты. Каждый этап работы с системой представлен в виде графической "картинки", на которой указаны необходимые действия и их результаты. Приводимые "подсказки" позволяют получить дополнительную информацию при выполнении конкретного действия. Возможности системы - выбор для контроля одного из перечисленных ингредиентов или всех вместе; источников - точечных, площадных или всех. Как описывалось ранее, система является обучающей, то есть строится на примере определенного набора пар ситуаций "метеоусловия Ç ингредиенты" Þ "источники выбросов" (ситуаций должно быть не менее двух: первая - обучающая, вторая - закрепляющая). В дальнейшем информация о ситуациях может накапливаться. На приведенной экранной форме заключительного этапа мониторинга определен источник, вносящий наибольший вклад в концентрацию вредных веществ и в документирование ситуации. Список литературы 1.Гаврилов А.С. и др. Экологический программный комплекс для персональных ЭВМ (теоретические основы и руководство пользователя ЭПК "ZONE"). • С-Пб, Гидрометеоиздат, 1992. -164 с. 2. Поспелов Д.А. Моделирование рассуждений. • М.: Радио и связь, -1990. -184 с. 3. Поспелов Г.С. Искусственный интеллект - основа новой информационной технологии. - М.: Наука, 1988. - 280 с. 4. Борисов А.Н., Крунберг ОА., Федоров И.П. Принятие решений на основе нечетких моделей / Примеры использования. - Рига: Знание, 1990. -184 с. 5. Бернштейн Л.С, Казупеев В.И., Коровин С.Я., Мелехов Н.Н. Параллельный процессор нечеткого вывода для ситуационных экспертных систем//Изв. АН СССР. Техн. кибернетика. 1990. - № 5. - С. 181-190. 6. Танака X., Цукияма Г., Асаи К. Модель нечеткой системы, основанная на логической структуре. - В кн.: Нечеткие множества и теория возможностей / Под ред. Р. Ягера. - М.: Радио и связь. - 1986. - 408 с. 7. Тихонов Н.Н. О задачах с нечетко заданной информацией. ДАН СССР, 1985.-Т. 20, №3 - С. 559-562. 8. Алиев Р.А., Абдикеев Н.М., Шахназаров М.И. Производственные системы с искусственным интеллектом. - М.: Радио и связь. - 1990. - 264 с. 9. Минаева О.Ю. Автоматизация испытаний строительных конструкций на основе эталонных принципов. - В кн.: Экспертные системы для анализа и реконструкции программного обеспечения вычислительных систем - К.: РИО КНИГА, 1992.-С. 71-84. 10. Кузьмин В.Б. Принятие решений в пространствах четких и нечетких бинарных отношении. - М.: Наука, 1988. -142 с. 11. Заде К.А. Основы нового подхода к анализу сложных систем и процессов принятия решении - В кн.: Математика сегодня. - М.: Знание, 1974. - С. 5-49. 12. Филимонова О.Ю. Автоматизация процессов неразрушающего контроля на основе новых информационных технологий / Автореферат диссертации на соискание ученой степени канд. техн. наук. - К.: КМУГА, 1994. - 16 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1064 |
Версия для печати |
| Статья опубликована в выпуске журнала № 1 за 1996 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Сравнительный анализ некоторых алгоритмов распознавания
- Алгоритмы и процедуры построения билинейных моделей непрерывных производств
- Интегрированная система «микросреда»
- Компьютерная интеграция и интеллектуализация производств на основе их унифицированных моделей
Назад, к списку статей




 , где аi -отдельная компонента измерения (вредный выброс - СО, СО2 или др., скорость и направление ветра, температура и др.); fia ( ) - "значимость" компоненты в ряду всех измерений или точность измерения (возможность получения достоверных измерений);
, где аi -отдельная компонента измерения (вредный выброс - СО, СО2 или др., скорость и направление ветра, температура и др.); fia ( ) - "значимость" компоненты в ряду всех измерений или точность измерения (возможность получения достоверных измерений);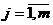 ; bj - источник загрязнений, определяемый мощностью выбросов, удалением от точки измерения и др., fjb ( ) - "значимость" источника выбросов с точки зрения его влияния на уровень концентрации вредных веществ в точке испытаний; fja ( ), fjb ( )=>[0,1]. * - операция maxmin- (или minmax-) композиции. Задача состоит в том, чтобы по результатам измерений Aj+1, Aj+2,...Aj+k определить возможные значения Bj+1, Bj+2,...Bj+ k соответственно, располагая матрицей отношений [R], определенной по результатам предварительных испытаний.
; bj - источник загрязнений, определяемый мощностью выбросов, удалением от точки измерения и др., fjb ( ) - "значимость" источника выбросов с точки зрения его влияния на уровень концентрации вредных веществ в точке испытаний; fja ( ), fjb ( )=>[0,1]. * - операция maxmin- (или minmax-) композиции. Задача состоит в том, чтобы по результатам измерений Aj+1, Aj+2,...Aj+k определить возможные значения Bj+1, Bj+2,...Bj+ k соответственно, располагая матрицей отношений [R], определенной по результатам предварительных испытаний.