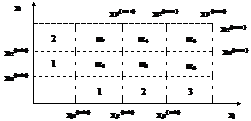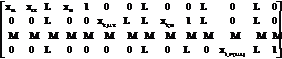Авторитетность издания
Добавить в закладки
Следующий номер на сайте
ПС проектирования системы управления непрерывными технологическими процессами
Аннотация:
Abstract:
| Авторы: Палюх Б.В. (pboris@tstu.tver.ru) - Тверской государственный технический университет (профессор), г. Тверь, Россия, доктор технических наук, Богатиков В.Н. (VNBGTK@mail.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, доктор технических наук, Вершков А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10286 |
Версия для печати |
При проектировании систем управления производственных процессов, характеризующихся наличием нештатных ситуаций, важную роль играет информация об эффективности функционирования и о характеристических свойствах химико-технологической системы (ХТС), которую можно получить либо в условиях эксплуатации системы, либо на основе вычислительного эксперимента, использующего различного рода имитационные модели технологических процессов. Необходимость в таких моделях возникает как при разработке систем управления новыми технологическими процессами, так и при эксплуатации ХТС, а также в случае совершенствования системы управления. Особую актуальность приобретают методы математического моделирования при исследовании критических и аварийных состояний химико-технологических процессов (ХТП), так как позволяют провести анализ возможных ситуаций с разной степенью проникновения в суть физико-химических явлений, происходящих в системе, не прибегая к физическому эксперименту. Разработка программных средств анализа и исследования различных состояний ХТС основывается на математических моделях отдельных процессов и системы в целом. Причем выбор типа математических моделей в значительной степени определяется целями их использования. Моделирование критических и аварийных ситуаций накладывает определенные требования на применяемые математические модели. Во-первых, модели должны учитывать не только возможные решения по смене технологических режимов, но и организационно-технические мероприятия, связанные с проведением ремонтов оборудования и систем управления. Для этих целей в модели должны быть заложены интегральные человеческие знания персонала данного производства, а также информация, получаемая в результате вычислительного эксперимента. Во-вторых, качественно меняется характер моделей, используемых в информационно-управляющих системах. По существу при моделировании критических и аварийных ситуаций осуществляется переход к дискретному представлению ХТП. Третьим требованием к моделям при рассмотрении критических и аварийных ситуаций является ограничение по времени, затрачиваемого на оценку состояния, выявление причин возникновения критических ситуаций и принятие решений по возврату в нормальное состояние. Данная работа посвящена разработке методики построения дискретных автоматных моделей отдельных ХТП и построению системы управления на их основе. ПРОЦЕССЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ КАК ОБЪЕКТЫ МАТЕМАТИЧЕСКОГО ИССЛЕДОВАНИЯ Каждый процесс, составляющий отдельный элемент макроструктуры ХТС, характеризуется вектором входных переменных qi, состояния xi, выходных переменных yi (i - текущий номер типового технологического процесса) и оператором: yi = Ti(qi, xi). (1) Здесь Ti - функциональный оператор, являющийся математической моделью ХТС и выполняющий отображение пространства переменных входа qi и текущего состояния xi в пространство выхода yi, соответствующее реальному технологическому процессу [1, 2]. Оператор Ti обладает сложной структурой, являющейся отражением, как правило, целого ряда элементарных технологических операций низшего уровня: химического превращения; диффузионного, конвективного и турбулент-ного переноса вещества и тепла и т.п. Этот оператор отражает совокупность линейных, нелинейных, распределенных в пространстве и переменных во времени процессов и имеет смешанную детерминированно-стохастическую природу. В явной форме оператор, осуществляющий отображение (1), представляет замкнутую систему дифференциальных, интегральных, интегродифференциальных уравнений и соотношений эмпирического характера, дополненную необходимыми начальными и граничными условиями [2]. В статье рассматриваются детерминированные функциональные операторы. Основными математическими свойствами уравнений, входящих в функциональные операторы, являются cуществование и единственность решений, а также непрерывная зависимость решений от параметров и от начальных значений, что позволяет сделать вывод о непрерывности области существования функциональных операторов для рабочих режимов работы [2]. ФОРМИРОВАНИЕ АЛФАВИТОВ ДИСКРЕТНОЙ АВТОМАТНОЙ МОДЕЛИ ТИПОВОГО ХИМИКО-ТЕХНОЛОГИЧЕСКОГО ОПЕРАТОРА Общая постановка задачи построения дискретных автоматных моделей рассмотрена в работе [3], где обоснована возможность построения данного класса моделей для непрерывных технологических процессов на основе комбинаторного метода включения и исключения [4, 5]. Наиболее общее описание детерминированного автомата можно задать в следующем виде [6, 7]: Adet = < X, A, Y, A(0),F,J > (2) X = {x1,...,xn} - входной алфавит (n-мощность входного алфавита); Y = {y1,...,ym} - выходной алфавит (m-мощность выходного алфавита); A = {a1,...,al} - алфавит состояний (l-мощность алфавита состояний); F = F(xs,ai(k-1),aj(k)) - функция перехода из одного из возможных состояний на k-ом шаге ai(k-1) в aj(k) (ai(k-1),aj(k) Î A) при появлении какого-либо символа xs (xs Î X); J = J(xs, ai(k-1), yq) - функция выхода автомата, который задает соответствие между состоянием автомата ai(k-1), поступившим символом на вход xs и выходным символом yq (yq Î Y). В работе [3] введение алфавитов входа, состояния и выхода функционального оператора Ti осуществляется на основе выделения непересекаемых областей в пространствах qi, xi и yi, которым ставятся в соответствие символы соответствующих алфавитов. Построение алфавитов проводится таким образом, чтобы существовало однозначное отображение множества пар (x,a) (где x Î X и a Î A) во множества A и Y (2), при этом практически одновременно с выделением элементов алфавита строится и таблица автоматных соответствий. Основное требование, которое при выде-лении областей алфавитов входа должно выполняться, заключается в следующем: необходимо осуществление перехода при заданной области начального элемента алфавита состо-яния и заданной области данного элемента алфавита входа только в область одного элемента алфавита состояний. Данное требование вытекает из свойств автоматных отображений [7, 8]. При таком подходе к построению алфавитов детерминированного автомата в зависимости от выбора алфавитов состояния и выхода могут быть получены различные алфавиты входных воздействий, то есть число алфавитов бесконечно. Рассмотрим частные случаи. Дифференциальные уравнения, описывающие поведение линейных систем, в общем виде можно записать следующим образом: dx /dt = Аx + b. (3) Здесь: x - вектор переменных состояния, чаще всего это концентрация субстанции (вещества или энергии); А - матрица коэффициентов, которая характеризует выходные потоки вещества или энергии ХТС; b - вектор, характеризующий входные потоки веществ или энергии; t - время. Очевидно, что множество точек, соответствующее определенному установившемуся режиму, определяется правой частью системы (3): Аx + b = 0. (4) Как известно, для технологических аппаратов существуют диапазоны параметров входных и выходных потоков, которые определяют элементы матрицы А и координаты вектора b, а также диапазоны переменных состояния, задающие режимы работы технологического процесса. Всегда существует система ограничений по переменным состояния, выделяющих тот или иной режим, следующего вида: xik(min) < xi < xik(max) (i=1,I; k=1,Ki) (5) или в векторной форме: xk(min) < x < xk(max) . (5*) Здесь: i - номер переменной состояния; k - номер технологического режима работы i-ой переменной. Наличие таких технологических ограничений на переменные состояния позволяет с какой угодно степенью дифференциации перечислять на основе чисто комбинаторного перебора возможные непересекаемые области существования переменных состояний или, как это было определено выше, элементы алфавита состояний ai, которые характеризуют конкретные технологические режимы работы ХТС. Общее число режимов или ai можно определить как произведение всех Ki(Q=Q*l , ..., l =Пкi) (Рис.1). i
Рис. 1. Определение числа элементов алфавита переменных состояния (Q*ij= KiKj = 2*3 = 6) Аналогично и для коэффициентов матрицы А и координат вектора b могут быть определены минимально и максимально допустимые значения. Хотя, как это уже оговорено, для конкретных вариантов расчета их можно брать постоянными величинами: aij(min)< aij < aij(max) (i=1,I; i=1,I), (6) bi(min) < bi < bi(max) (i=1,I). (7) Обозначим область существования коэффициентов матрицы А и координат вектора b, определяемую неравенствами (6, 7), в соответствии c введенными обозначениями через X. Cистема (4) определяет уравнение гиперплоскости относительно вектора x. Если рассматривать координаты x как константы, а элементы матрицы А и вектора b как переменные, принадлежащие области ограничений, задаваемой неравенствами (6, 7), то в результате получим, что система уравнений (4) будет определять также уравнение гиперплоскости, но уже относительно элементов матрицы А и координат вектора b. Введем матрицу Xq, формирующуюся из элементов векторов xq(min) и xq(max), а также из коэффициентов при координатах вектора b, и образуем вектор переменных z, в который входят все элементы матрицы А и вектора b. Матрица X для произвольного aq-го элемента алфавита будет представлена в следующем виде:
Здесь x11, x2,I+2,..., xI,(I-1)(I+1) = x1, и т.д. xI,I(I+1)=1. Матрица X будет иметь размерность IxI(I+1). Вектор переменных zq aq-го режима запишется следующим образом: z = (z1, z2, ... , zL), где соответствие элементов таково: z1 = a11, z2 = a12, ... , zI = a1I, zI+1 = b1, ... и т.д. Размерность вектора L=I(I+1). На основе приведенных неравенств (5) и системы (4) можно получить системы линейных ограничений, выделяющие в области X, области элементов матрицы А и вектора b или вектора z, принадлежащие некоторому элементу алфавита входа, области xq, соотносящихся с некоторой областью элемента алфавита состояний aq. Естественно, при этом необходимо учитывать систему ограничений (6, 7): Xq< z < 0. (8) Xq> z > 0. (9) Здесь Xq<, Xq> – матрицы Xq, образованные нижней и верхней границами для q-го режима работы по координатам переменных состояния x на основе ограничений (5) aq элемента алфавита состояний. Можно сделать такие утверждения: - область, ограниченная неравенствами (8¸9) xq (xq принадлежит X), будет выпукла; - системы (10 ¸ 13) непротиворечивы; - xi Ç xj = Æ (i,j = 1,Q; i - j). Доказательство данных утверждений можно найти, например, в теории выпуклого анализа и линейных неравенств [8, 9], а также в работе [10]. Правила для образования матриц Xq< и Xq> для q-го режима будут следующие: - если формируются ограничения (5) и zh < 0 (ему соответствует aij, где i=entire(h/(I+1)) и j= h-i; entire(s) - функция выделения целой части s), то соответствующий элемент матрицы Xq для q-го режима будет определяться как xij=xp(max) (здесь p=j-entire(j/(I +1)); - если формируются ограничения (5) и zh > 0, то xij=xp(min); - если формируются ограничения (6) и zh < 0, то xij=xp(max); - если формируются ограничения (6) и zh > 0, то xij=xp(min). Для классов объектов, описываемых нелинейными дифференциальными уравнениями и дифференциальными уравнениями в частных производных, показана возможность применения метода разделения состояний на основе линейной аппроксимации систем уравнений, входящих в математическую модель [10]. ОБОБЩЕННОЕ ОПИСАНИЕ ПАКЕТА ПРОГРАММ ПРОЕКТИРОВАНИЯ СИСТЕМЫ УПРАВЛЕНИЯ НА ОСНОВЕ КОНЕЧНЫХ АВТОМАТОВ НЕПРЕРЫВНЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ В целом, используя новый информационный подход [11], можно выделить следующие основные этапы построения информационно-управляющих систем для оценки состояния ХТС и возможности ее выхода в критические и аварийные режимы: - построение полной модели ХТС [12]; - проведение вычислительного эксперимента с целью выделения областей существования параметров для различных режимов работы; - построение дискретной модели ХТС; - построение информационно-управляющей системы, которое включает в себя выбор или создание экспертной системы и базы данных [13, 14]; - насыщение базы знаний и базы данных необходимой информацией о ХТС; - проведение вычислительного эксперимента с целью исследования построенной информационно-управляющей системы оценки критических и аварийных состояний ХТС для выявления узких мест и принятия дальнейших решений по возможному совершенствованию ее организационной структуры [12]. В настоящее время стандартом программной среды стала “Архитектура среды для разработки приложений” (SAA, Systems Application Architecture), разработанная фирмой IBM в 1988 году. Часть этой архитектуры, отвечающая за взаимодействие программы с пользователем, называется “Единый доступ пользователя” (CUA, Common User Access) и определяет правила построения интерфейса. Рассмотрим описание этапов проектирования системы управления непрерывным технологическим процессом. Построение полной модели ХТП начинается с построения ставших классическими математических моделей на основе обыкновенных дифференциальных уравнений и уравнений в частных производных. Математические модели процессов могут включать формулы для расчета физико-химических величин, различные системы линейных и нелинейных алгебраических уравнений. Процесс решения чаще всего строится по следующей схеме: - проводится расчет физико-химических величин для заданных условий прохождения процесса; - решается система линейных либо нелинейных алгебраических уравнений (возникновение таких систем уравнений чаще всего связано с наличием каких-либо явлений, сопровождающих технологический процесс или участвующих в нем, временные характеристики которых различны; кроме того, такие системы возникают при решении дифференциальных уравнений методом сеток); - выполняется расчет производных и осуществляются вычисления новых значений пе-ременных для данного шага (при решении дифференциальных уравнений в частных производных методом сеток данный шаг отсутствует); - анализируется окончание решения. Моделирующая программа такого класса должна базироваться на применении стандартного интерфейса и включать в себя: - базу данных патентной и библиографической информации с возможностью поиска данных по темам, ключевым словам и фамилиям авторов; - базу данных для хранения экспериментальных результатов с возможностью предварительной обработки и выборки данных для передачи их в другие модули на дальнейшую обработку; - систему для построения графиков и вы-дачи на печать различных таблиц с результатами; - диалоговую систему подготовки экспериментальной информации для расчетов физико-химических констант и построения математических моделей процесса; - библиотеку подпрограмм реализации стандартных методов расчета для предыдущего модуля; - систему подсказок по всем видам возможных работ, осуществляемых в подсистеме моделирования. Рассмотрим конкретную структуру подсистемы моделирования, ее представление на экране компьютера и взаимодействие с программными модулями.
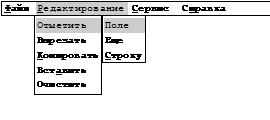
Рис.2. Вид экрана: открытых файлов нет, выбор типа создаваемого файла Любая работа системы начинается с открытия файлов с хранящейся информацией, поэтому первым пунктом полосы действий является слово "Файл", обозначающее меню различных операций с файлами. Если никаких файлов еще не открыто, в полосе действий доступно еще только два пункта - "Сервис", с помощью которого можно менять различные внутренние установки (цвета экрана, количество строк) и вызывать калькулятор, и "Помощь" с различными видами подсказок по работе системы. Момент создания нового файла с помощью этого меню изображен на рисунке 2. После открытия (создания) для работы какого-либо файла в полосе действий появляются новые пункты, причем количество их будет разным для разных типов файлов, в зависимости от тех действий, которые возможны для данного типа файла. Все данные в ИС организованы в виде файлов двух основных типов – справочников, предазначенных для хранения библиографических данных, и лабораторных журналов, в которых хранятся результаты экспериментов. Рассмотрим варианты работы пользователя в интегрированной системе с разными типами файлов. В системе имеется две базы данных, информация в которых представлена в виде таблиц. Форма этих таблиц (количество столбцов, их названия, ширина, тип данных, содержащихся в них) может быть либо стандартной, (например для библиографического справочника), либо полностью определяемой пользователем (для экспериментальных данных). Для хранения информации, по которой создается таблица определенной формы, предназначен файл типа шаблон. Пользователь должен иметь возможность изменять его. Значит при открытии или создании файла-шаблона в полосе действий должен появиться пункт “Редактирование”, дающий доступ к меню различных операций редактирования. Точно так же пользователь должен иметь возможность изменять информацию, хранящуюся в таблицах баз данных, поэтому при открытии или создании библиографического справочника или таблицы экспериментальных данных и этот пункт должен быть доступен. Меню “Редактирование” дает возможность выбрать одну из доступных операций манипулирования информацией таблицы ( рис. 3).
Рис.3. Вид экрана: открыт файл шаблона, выбор объекта выделения Файл шаблона предназначен только для хранения информации о форме таблиц пользователя. Никаких действий, кроме открытия, редактирования и сохранения, с ним производить не нужно. Поэтому полоса действий после открытия файла шаблона будет иметь следующие пункты: “Файл”, “Редактировать”, “Сервис” и “Помощь”.
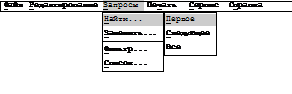
Рис.4. Вид экрана: открыт файл библиографии, формирование запроса на поиск База данных патентной и библиографической информации, как уже было сказано, должна давать возможность организации различных запросов для поиска необходимой информации. Кроме этого, очевидна необходимость получения твердой копии выбранных сведений. Поэтому при открытии файла этой базы (файла справочника) в полосе действий, кроме пункта “Редактирование”, должны появиться пункты "Запросы" и "Печать". Меню “Запросы” (рис. 4) предназначено для организации различных запросов на поиск данных и формирование списка результатов поиска. При работе с базой данных экспериментальных результатов необходимы возможность поиска данных в базе и печать отобранной информации, но, кроме того, следует иметь реальность обработки этих данных. Значит, в полосе действий должно появиться меню ”Обработка” для выбора конкретной работы с данными (рис. 5).
Рис.5. Вид экрана: открыт файл с экспериментальными данными, выбор способа обработки данных Меню "Печать" предназначено для получения печатных копий результатов работы с интегрированной системой. Оно содержит следующие пункты: - "Печать" для установки направления печати (принтер или файл) и начала процесса распечатки отобранного материала; - "Параметры" для установки различных параметров страницы и ее оформления (длина, ширина, межстрочный интервал, верхние, нижние и боковые отступы, нумерация, колонтитулы); - "Просмотр" для предварительного просмотра на экране текста в том виде, в каком он будет напечатан; - "Принтер" для выбора принтера из набора стандартных или с добавлением в этот набор своего путем ввода названия и основных управляющих последовательностей. Взаимодействие описанной подсистемы меню с программными модулями заключается в следующем: при выборе типа открываемого файла автоматически выбирается соответствующая база данных. Затем при помощи пунктов "Редактирование" и "Запросы" из полосы действий осуществляются основные виды работ для обеих баз – ввод, изменение, удаление хранимой информации, организация различных запросов. При помощи пункта "Печать" происходит взаимодействие баз данных и системы печати отчетной информации. Пункт "Обработка" представляет выход диалоговой системы подготовки информации для расчетов, которая затем вызывает требуемые методы из библиотеки и производит с их помощью необходимые вычисления. Система подсказок может быть вызвана в любой момент через пункт "Помощь" либо нажатием клавиши F1. Выше приведено довольно подробное описание подсистемы построения математической модели непрерывного технологического процесса. Завершаются работы по разработке модели получением файла программы, написанного на удобном для пользователя языке программирования (например фортране или паскале) и созданием баз исходных данных, необходимых для выполнения исследования режимов работы технологического процесса. Следующим этапом проектирования системы управления является вычислительный эксперимент, основные цели которого выявление границ различных режимов работы объекта управления, определение областей линеаризации процессов, описываемых нелинейными системами уравнений, определение числа ячеечных моделей для объектов с распределенными параметрами, т.е. проведение вычислительного эксперимента на математической модели процесса. Для этого при установке программных средств системы проектирования необходимо предусмотреть задание путей к соответствующим трансляторам, к рабочим каталогам с файлами, содержащими программные модули исходной программы, и файлам баз данных. Подсистема вычислительного эксперимента модели должна обеспечивать автоматический запуск исходной программы моделирования с различными режимами решения задачи, с подключением программных модулей библиотеки стандартных программ, а также использование графических пакетов системы. После проведения всего комплекса работ, связанного с определением границ режимов работы технологического процесса, выполняется этап построения дискретной модели, который заключается в формировании файлов данных как поступающих с объекта, так и полученных в результате вычислений, необходимых для проведения вычислений по дискретной модели (создание базы данных). Кроме того, на этом этапе формируется граф событийных процессов, происходящих при функционировании технологического объекта в соответствии с описанной методикой, на основе которого реализуется порождение команд автоматом управления. На данном этапе осуществляется увязка основных компонент программы моделирования системы управления, построенной на основе дискретной автоматной модели процесса. Это увязка программы работы дискретной модели технологического процесса, базы данных и автомата управления. Фактически здесь выполняется построение информационно-управляющей системы и насыщение базы знаний и базы данных необходимой информацией о ХТС. Следует отметить, что основное назначение всех описанных последовательностей работ заключается в подготовке информационных массивов и программных модулей для проведения эксперимента на математической модели системы управления технологическим процессом. Поэтому для ее исследования в режимах, соответствующих реальным условиям, в некоторых случаях может понадобиться генерация исходной информации на основе законов распределения случайных величин, и на данном этапе должно быть осуществлено подключение соответствующих программных средств. Заключительным моментом проектирования системы управления на основе конечных автоматов является вычислительный эксперимент непосредственно на самой модели системы, при анализе результатов которого выявляются некорректности в ее работе. Список литературы 1. Кафаров В.В. Методы кибернетики в химии и химической технологии. - М.: Химия, 1971. - 496 с. 2. Дорохов И.Н., Кафаров В.В. Системный анализ процессов химической технологии. - М.: Наука, 1976. - 500 с. 3. Богатиков В.Н. Построение дискретных автоматных моделей химико-технологических систем (ХТС). - Апатиты, 1994. - 24 с.-(Препр.). 4. Рыбников К.А. Введение в комбинаторный анализ. - М.: Изд-во Московского ун-та, 1972. - 256 с. 5. Холл М. Комбинаторика. - М.: Мир, 1970. - 425 с. 6. Чирков М.К. Основы общей теории конечных автоматов. - Л.: Изд-во ЛГУ, 1975. - 282 с. 7. Глушков В.М. Синтез цифровых автоматов. - М.: Физматлит, 1962. - 476 с. 8. Белоусов Е.Г. Введение в выпуклый анализ и целочисленное программирование. - М.: Изд-во Московского ун-та, 1976. - 1977. - 196 с. 9. Фан Цзи. О системах линейных неравенств. - В кн.: Линейные неравенства. - М., 1959. 10. Богатиков В.Н., Борисов А.Л. Метод разделения состояний химико-технологических систем // Синтез систем вычислительного эксперимента. - Апатиты, 1994. - С.39-52. 11. Поспелов Г.С. Искусственный интеллект - основа новой информационной технологии.- М.: Наука, 1988.-272 с. 12. Богатиков В.Н. Технология моделирования химико-технологических систем. // Вычислительный эксперимент и моделирование в системах "Технологические процессы - природные комплексы". - Апатиты 1992. - С.77-81. 13. Уотермен Д. Руководство по экспертным системам. - М.: Мир, 1989. - 388 с. 14. Системы управления базами данных и знаний./ Справочное изд. под ред. Наумова А.Н. - М.: Финансы и статистика, 1991. - 352 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1112 |
Версия для печати |
| Статья опубликована в выпуске журнала № 2 за 1995 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- Система визуализации реального времени на основе программируемых сигнальных процессоров
- Интерактивная процедура построения модели тренда для экономических показателей
- Исследовательское проектирование в кораблестроении на основе гибридных экспертных систем
- Комплекс программных средств для аналитических иерархических процессов экспертного оценивания
Назад, к списку статей