Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Эвристические и точные методы программной конвейеризации циклов
Аннотация:
Abstract:
| Авторы: Вьюкова Н.И. (niva@niisi.msk.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, Галатенко В.А. (galat@niisi.msk.ru) - НИИСИ РАН, г. Москва (зав. сектором автоматизации программирования), г. Москва, Россия, кандидат физико-математических наук, Самборский С.В. (sambor@niisi.msk.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15756 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
Параллелизм операций в пределах одной итерации программного цикла, как правило, недостаточен для эффективного использования вычислительных ресурсов современных суперскалярных архитектур и архитектур с широким командным словом (VLIW – very large instruction word). Программная конвейеризация – эффективный метод оптимизации циклов, позволяющий использовать параллелизм операций, относящихся к разным итерациям цикла. Цель этой оптимизации – построить расписание, при котором последовательные итерации цикла запускались бы с некоторым постоянным интервалом, и свести к минимуму этот интервал за счет перекрытия различных итераций исходного цикла. Выигрыш достигается благодаря тому, что операции из одной итерации исходного цикла могут запускаться в разных итерациях конвейеризованного цикла. При этом длительные операции запускаются заранее, чтобы их результаты были готовы к моменту, когда они понадобятся. Таким образом, исключаются простои и лучше используются ресурсы процессора. Пример 1 иллюстрирует эффект программной конвейеризации. Пример 1. for (i=0; i Z[i]=k*X[i]+Y[i]
0 Ld x, Ld y 1 t=k*x
2 3 4 5 z=t+y 6 St z Выполнение каждой итерации занимает 7 тактов, и из-за зависимостей по данным параллелизм процессора практически не используется. На рисунке 2 приведено расписание для цикла из примера 1, полученное в результате конвейеризации. В теле (ядре) конвейеризованного цикла совмещаются команды трех итераций из диапазона четырех соседних итераций; за счет этого время выполнения одной итерации конвейеризованного цикла составляет всего 2 такта (вместо 7 для исходного цикла). Таким образом, конвейеризация циклов может давать значительный прирост производительности, позволяя в ряде случаев полностью использовать ресурсы процессора. Тело конвейеризованного цикла называют ядром. Для сохранения эквивалентности вычислений по отношению к исходному циклу перед телом конвейеризованного цикла добавляется пролог, содержащий команды из начальных итераций, а в конце – эпилог, включающий команды из завершающих итераций, которые не выполняются в ядре цикла; число повторений цикла уменьшается на величину, равную глубине перекрытия итераций (которая в данном примере равна 3).
Периодическим расписанием цикла называется отображение T, которое каждой команде c тела исходного цикла и каждой итерации j сопоставляет время (номер такта) запуска команды c в итерации j, такое, что T(c,j+1)=T(c,j)+II, где II – интервал запуска цикла (initiation interval). Интервал запуска определяет время выполнения одной итерации конвейеризованного цикла. Корректным расписанием цикла называется расписание, которое обеспечивает соблюдение всех зависимостей по данным и не вызывает конфликтов по использованию ресурсов процессора или задержек по неготовности данных. Задача программной конвейеризации – построение корректного периодического расписания цикла, ее целевая функция – минимизация II. Величина II ограничена снизу двумя значениями, которые определяются требованием корректности расписания, свойствами процессора и зависимостями по данным, имеющимся в конвейеризуемом цикле. Первая оценка, обозначаемая обычно ResMII, обусловлена количеством ресурсов процессора, доступных на каждом такте. Ресурсами в данном контексте могут быть функциональные устройства, пропускная способность памяти, число команд, которые можно одновременно подать на исполнение, поля в командном слове для VLIW-архитектуры. Пусть имеются ресурсы разных типов, причем на каждом такте доступно не более ri единиц i-го ресурса, и пусть потребность в i-м ресурсе на одну итерацию цикла равна ni. Очевидно, что должно иметь место неравенство II³ResMII=maxi(ni/ri). Оценка по зависимостям RecMII возникает из структуры зависимостей между командами тела цикла. Зависимости описываются графом зависимостей по данным (DDG – Data Dependence Graph), в дальнейшем называемом графом зависимостей. DDG= =(V,E), где V – множество вершин, совпадающее с множеством команд ci исходного цикла, а E – множество дуг, которые соответствуют зависимостям команд: (c1,c2)ÎEÛ(c2 использует данные, производимые c1) Ú ((c1 предшествует c2) Ù (c1 осуществляет доступ к памяти, а c2 может записывать значение по тому же адресу, что и c1)). Таким образом, DDG отражает все истинные зависимости («запись–чтение»), а также ложные зависимости по памяти («чтение–запись» и «запись–запись»). Ложные зависимости по данным, находящимся на регистрах, игнорируются. Так, в примере 1 имеет место зависимость «чтение–запись» между командой z=t+y и командой t=2*x следующей итерации, но в DDG она не учитывается. Дуги DDG помечены двумя неотрицательными целочисленными значениями: латентностью (lat) и дистанцией (dist). Латентность определяет, через сколько тактов может быть запущена команда c2 после запуска команды c1, чтобы результаты c1 были готовы к тому моменту, когда они потребуются команде c2. Дистанция равна относительному номеру итерации, в которой команда c2 использует результат c1. Если результат c1 используется в той же итерации исходного цикла, дистанция равна нулю, если в следующей – единице, и т.д. Общее ограничение на применимость любого метода конвейеризации цикла состоит в том, что дистанции всех зависимостей должны быть постоянны и известны на стадии компиляции. Это называется однородностью зависимостей. Если дистанции неизвестны или неоднородны, можно считать ненулевые дистанции равными 1. Пример 2 иллюстрирует понятие зависимости с ненулевой дистанцией. Пример 2. for (i=0; i B[i]=B[i-2]+C
Рис. 3 На рисунке 3 показан граф зависимостей для этого примера в предполо- жении, что сложение выполняется за 4 такта, а остальные команды занимают 1 такт. Команда t1=B[i-2] читает значение, записанное командой B[i2]=t2 двумя итерациями раньше, то есть между этими командами имеет место зависимость с дистанцией 2. Антизависимости по памяти в этом примере отсутствуют. Если команда c2 зависит от команды c1 с латентностью lat12 и дистанцией dist12, для корректного расписания должно выполняться неравенство T(c2) + dist12 ×II ³ T(c1) + lat12. (1) Рассмотрим произвольный цикл в DDG (чтобы отличать циклы в графе зависимостей от компилируемых циклов программы, будем в дальнейшем называть циклы в графе зависимостей контурами, имея в виду обычные циклы в ориентированном графе), обозначим входящие в него команды c1, c2, ... , ck: команда c2 зависит от c1, c3 зависит от c2 и т.д., а команда c1 зависит от ck. Просуммировав неравенства (1) по всем зависимостям контура и сократив T(ci), получим неравенство
где е – зависимости, образующие контур w. Поскольку (2) верно для всех контуров DDG, Программная конвейеризация циклов методом планирования по модулю Различают два основных класса алгоритмов конвейеризации. Алгоритмы типа «перемещаем–затем–планируем», называемые также алгоритмами перемещения кода (code motion), выстраивают ядро конвейеризованного цикла путем последовательного циклического перемещения команд снизу вверх с последующим планированием и выбором наилучшего варианта. Алгоритмы второго класса, вместо того чтобы строить расписание цикла путем последовательных трансформаций исходного цикла, формируют ядро цикла из команд исходного цикла. В этом классе, в свою очередь, выделяются алгоритмы, основанные на развертке и упаковке цикла, и алгоритмы планирования по модулю. В промышленных компиляторах наиболее широко используется метод планирования по модулю, поскольку он эффективен, может быть расширен для применения к широкому классу циклов, включая циклы, содержащие условные конструкции, циклы, число повторений которых неизвестно перед началом выполнения, а также циклы с множественными выходами. Существуют различные эвристические алгоритмы планирования по модулю, которые для современных процессорных архитектур позволяют находить оптимальные или близкие к оптимальным решения указанной задачи; в рамках этого метода могут быть применены также подходы, позволяющие находить точное решение задачи программной конвейеризации циклов. Рассмотрим общую схему работы алгоритмов планирования по модулю. Определение диапазона II. Сначала определяется диапазон значений II, в котором будет производиться поиск решения, то есть расписания цикла. Нижней границей II, обозначаемой обычно MII, берется значение max(RecMII, ResMII). Верхней границей II может быть взято значение, на единицу меньшее, чем число тактов, требуемых для выполнения одной итерации исходного цикла. Перебор II и планирование. Для значений II из этого диапазона делаются попытки построить расписание с данным интервалом запуска. Расписание с минимальным II из указанного диапазона, если оно было найдено, и будет решением задачи. Как правило, используют последовательный перебор значений II, начиная с MII; последовательный поиск предпочтительнее, например, бинарного, поскольку в большинстве случаев удается найти решение, близкое к MII. Для нахождения расписания при фиксированных II могут применяться как эвристические, так и точные методы планирования. Негативным следствием программной конвейеризации циклов, как и других агрессивных методов распараллеливания кода, является усиление дефицита регистров вследствие перекрытия итераций исходного цикла. Поэтому большинство эвристических методов планирования по модулю включают эвристики для минимизации требований по регистрам. Применяются также методы постпроцессирования расписаний циклов с целью сокращения числа требуемых регистров, такие как Stage Scheduling. В точных методах планирования циклов обычно решается задача нахождения расписания с минимизацией требований по регистрам среди расписаний с минимальным II. Эвристические методы планирования Задача нахождения расписания для заданного II является NP-полной, поэтому в промышленных компиляторах, как правило, применяются эвристические алгоритмы. Сначала команды упорядочиваются некоторым образом, затем делается попытка каждой из них назначить номер такта, на котором она будет выполняться. Эвристические алгоритмы планирования по модулю различаются способами начального упорядочения команд и эвристиками, используемыми для поиска подходящего такта (позиции в расписании). На каждом шаге работы алгоритма строится корректное частичное расписание; это означает, что назначения позиций для команд не должны нарушать ограничения по ресурсам или вызывать задержки по неготовности аргументов. Для контроля ограничений по ресурсам применяется модульная таблица резервирования (MRT – modulo reservation table). Высота этой таблицы равна II, а столбцы соответствуют имеющимся ресурсам (функциональным устройствам процессора). Если ресурс r используется на такте t, в таблице помечается элемент MRT[r, t mod II]. Если для очередной команды не удается найти подходящую позицию, предусматривается либо увеличение II, либо откат ранее выполненных шагов. Алгоритмы с откатами называют итеративными. Для того чтобы ограничить количество откатов в итеративных алгоритмах, устанавливают некоторый бюджет перебора, по исчерпании которого перебор прекращается и начинается поиск решения для следующего по возрастанию значения II. Итеративные алгоритмы даже при отсутствии бюджетного ограничения не гарантируют перебор всех частичных расписаний; вместо этого они могут циклически перебирать некоторое подмножество расписаний. Рассмотрим особенности ряда известных алгоритмов эвристического планирования по модулю. Iterative Modulo Scheduling (IMS) – итеративный алгоритм, который упорядочивает команды в соответствии с их высотой в графе зависимостей и ищет для каждой команды наиболее раннюю допустимую с точки зрения отсутствия конфликтов по ресурсам позицию. Если для очередной команды не находится подходящей позиции, какая-то из ранее спланированных команд возвращается в очередь планирования, чтобы освободить место для данной команды. Возможность откатов в пределах заданного бюджета – ключевое свойство IMS, благодаря которому этот алгоритм обеспечивает в некоторых случаях меньшие значения II, чем неитеративные алгоритмы. Недостаток IMS – отсутствие эвристик, ориентированных на минимизацию потребности в регистрах. Slack Modulo Scheduling (Slack) предполагает двунаправленное планирование в отличие от большинства других алгоритмов, где поиск свободного слота для команды ведется сверху вниз или снизу вверх. Еще одна отличительная черта данного метода – способ упорядочения команд в очереди на планирование: команды упорядочиваются по возрастанию своей степени мобильности. Степень мобильности команды по отношению к некоторому частичному расписанию измеряется числом слотов, в которые она могла бы быть запланирована. Позиция для очередной команды выбирается таким образом, чтобы минимизировать суммарное время жизни ее входных и выходных аргументов. Данная эвристика направлена на снижение потребности в регистрах. Slack, как и IMS, является итеративным методом. Integrated Register Sensitive Iterative Software Pipelining (IRIS) отличается от IMS тем, что при планировании команд применяются эвристики минимизации потребности в регистрах. Для команды назначается самая ранняя либо самая поздняя позиция таким образом, чтобы минимизировать интервалы жизни значений. Swing Modulo Scheduling (SMS) – неитеративный и в силу этого весьма быстрый алгоритм планирования по модулю. Команды, принадлежащие циклам в графе зависимостей, изначально упорядочиваются по значению RecMII соответствующего цикла; в качестве вторичного фактора учитывается степень критичности пути, которому принадлежит команда. Способ упорядочения команд гарантирует, что в очереди планирования перед данной командой могут находиться только ее предшественники или только преемники, но не те и другие одновременно. Выбор позиции в расписании для очередной команды осуществляется таким образом, чтобы минимизировать время жизни входных регистров (если уже запланированы предшественники этой команды) или выходных регистров (если уже запланированы ее преемники). Эта стратегия направлена на минимизацию потребности в регистрах. Разнообразие эвристик, используемых в методах планирования по модулю, говорит о том, что не существует универсального подхода, удовлетворительного по всем критериям и для всех микропроцессорных архитектур. Экспериментальные исследования кода, полученного при помощи различных эвристических методов планирования по модулю, показывают, что для «хороших» архитектур (с высокой степенью параллелизма на уровне команд, полностью конвейеризованными операциями, большим числом регистров) расписания, генерируемые эвристическими алгоритмами планирования по модулю, близки к оптимальным как по величине II, так и по числу используемых регистров; однако для «неудобных» архитектур (с неконвейеризованными или неполностью конвейеризованными операциями и т.п.) расхождение между расписаниями, генерируемыми эвристическими алгоритмами, и оптимальными расписаниями становится значительным. Точные методы планирования по модулю Точные методы планирования циклов требуют больших вычислительных затрат и изначально развивались преимущественно как средства, при помощи которых разработчики компиляторов могли бы оценивать качество эвристических алгоритмов и настраивать эвристики. Они также могут применяться как опция компиляции, когда требуется достижение максимальной производительности генерируемого кода, а время компиляции имеет второстепенное значение. Существуют переборные алгоритмы для нахождения оптимальных расписаний, требующие очень больших вычислительных затрат [1]. Другой подход заключается в том, что задача планирования циклов формулируется в виде задачи целочисленного линейного программирования (ЦЛП). Задача ЦЛП представляет собой нахождение целочисленного оптимума в задаче линейного программирования. Это хорошо изученная NP-полная задача. Для практического решения ЦЛП-задач разработаны пакеты программ – солверы, среди которых есть как коммерческие, так и свободно доступные в исходных текстах. В [2] представлена формулировка ЦЛП-задачи нахождения расписания с минимальным II и минимальной средней длиной интервалов жизни значений без ограничений по ресурсам. В этой и ряде других работ требования по регистрам аппроксимируются посредством суммарного размера буферов по всем переменным, резервируемых в течение промежутка времени, кратного II. В [3] формулировка из работы [2] дополнена ограничениями по ресурсам для полностью конвейеризованных функциональных устройств. Авторы работы [4] независимо сформулировали ЦЛП-задачу планирования циклов для машин со сложными зависимостями по ресурсам, предусмотрев учет ограничений по ресурсам и фактическое назначение ресурсов для команд цикла. Их подход полезен для случаев, когда задача назначения ресурсов нетривиальна, однако он требует больших вычислительных затрат. Когда тривиальное назначение ресурсов возможно без развертки цикла, предпочтительна более компактная формулировка задачи планирования [5]. В [6] сформулирована модель, минимизирующая требования по регистрам путем совместного решения задач планирования и назначения регистров. При этом добавляется необходимое число команд копирования значений, время жизни которых превышает II. Этот подход приемлем для машин с высокой степенью параллелизма, когда для дополнительно генерируемых пересылок, как правило, найдутся свободные позиции и производительность не будет снижена. Если это не так, предпочтителен подход [5], который может требовать развертки цикла для назначения оптимального числа регистров, но не предполагает вставки в цикл дополнительных пересылок. В работе [1] представлен первый опыт внедрения и использования ЦЛП для конвейеризации циклов в промышленном компиляторе (MIPSPro для микропроцессора MIPS R8000). Целью исследования было оценить целесообразность данного подхода для практического применения и те проблемы, которые могут при этом возникнуть. В формулировке ЦЛП-задачи учтены ограничения по ресурсам и на число регистров, аппроксимируемых суммарным размером буферов. Возможности практического применения ЦЛП-подхода (с учетом производительности ЭВМ, на которых выполнялась компиляция) ограничивались циклами, тело которых содержало не более 14 команд. Тестирование полученного кода показало, что минимизация числа регистров не имеет большого значения при условии, что физических регистров достаточно. Вместо этого имеет смысл учесть другие факторы, которые могут влиять на производительность. Например, специфические для MIPS R8000 ограничения на доступ к памяти, что позволило получить ощутимый выигрыш в производительности генерируемого кода. Опыт этой работы показал также важность исследований, направленных на разработку формулировок ЦЛП-задачи планирования, допускающих эффективное решение. В связи с этим интересны также методы, ускоряющие поиск решения. Гибкость подхода с использованием ЦЛП позволяет решать задачи планирования с различными критериями оптимизации, такими как минимизация энергозатрат или минимизация суммарной стоимости функциональных устройств (в системах синтеза аппаратных расширений). Распределение регистров для конвейеризованных циклов Число физических регистров, необходимых для данного расписания цикла, обозначается MaxLive; оно равно максимальному (по всем тактам выполнения ядра) числу открытых интервалов жизни значений на регистрах. Интервал жизни значения на регистре начинается с такта, на котором значение присваивается регистру, и заканчивается тактом, на котором это значение в последний раз используется какой-либо командой. Доказано: если разрешить развертку конвейеризованного цикла, оценка MaxLive достижима, то есть число физических регистров, равное MaxLive, не только необходимое, но и достаточное. На рисунке 4 показаны интервалы жизни значений конвейеризованного цикла из примера 1 в развернутом (рис. 4а) и свернутом (рис. 4б) виде. Величина MaxLive для этого примера равна 8.
Вставка пересылок. Перед присваиванием очередного значения прежнее копируется на другой регистр, значение которого может быть предварительно скопировано еще на один регистр, и т.д. Число операций копирования на единицу меньше размера буфера. Развертка (MVE – Modulo Variable Expansion). Выполняется развертка цикла, в каждой копии тела цикла для хранения значений используется свой набор регистров. Если процессор не обладает высокой степенью параллелизма на уровне команд, вставка в код дополнительных пересылок приводит к снижению производительности, и поэтому предпочтительным является метод MVE. Он заключается в том, что тело (ядро) конвейеризованного цикла развертывается с некоторой кратностью и в разных экземплярах тела цикла для хранения «долгоживущих» значений переменной используются разные регистры. Таким образом, одновременно хранятся значения переменных от разных итераций. Следует отметить: если число итераций цикла неизвестно на стадии компиляции, для каждого экземпляра тела цикла необходимо сгенерировать отдельный эпилог, использующий соответствующий набор регистров. При кратности развертки, равной наименьшему общему кратному размеров буферов по всем переменным, для каждой переменной можно выделить количество регистров, равное размеру ее буфера. Если вычисленная таким образом кратность развертки слишком велика, на практике могут применяться меньшие значения (например, максимум по всем размерам буферов), но тогда регистров может потребоваться больше, чем суммарный размер буферов. Недостаток описанных методов в том, что они не всегда обеспечивают распределение регистров в пределах величины MaxLive. Рассмотрим пример расписания цикла: for (i=0; i a[i+2]=b[i]+1 b[i+2]=c[i]+1 c[i+2]=a[i]+1 Пусть процессор позволяет запускать одну команду на такт и время выполнения каждой команды – один такт, то есть II=3. Интервал жизни каждого значения равен 8, и величина Maxlive также равна 8. При использовании MVE или копировании регистров для цикла потребуется 9 регистров. Причина в том, что эти методы (как и ротация регистрового файла) предполагают округление интервалов жизни вверх до значений, кратных II, а для распределения регистров в пределах MaxLive необходимо учитывать точные границы интервалов жизни. Существует метод для определения минимальной кратности развертки цикла, достаточной для распределения регистров в пределах величины MaxLive. Однако эта минимальная кратность может быть довольно большой (для рассмотренного примера она равна 8). При большой кратности развертки тело цикла может не поместиться в кэш команд, что приведет к снижению производительности. В [7] предложен быстрый эвристический алгоритм распределения регистров U&M (Unroll & Move) в конвейеризованных циклах, в котором комбинируется использование пересылок и развертки. Метод обеспечивает использование MaxLive-регистров при небольшой кратности развертки цикла. Недостатком U&M является использование пересылок, из-за которых может увеличиться интервал запуска. Если в полученном расписании требуемое число регистров превышает число физических, на стадии распределения регистров приходится временно высвобождать некоторые регистры, добавляя в программу код для их сохранения в памяти и последующего восстановления (spill-код), что снижает производительность программы. Чтобы обеспечить контроль над этим эффектом, могут применяться следующие подходы. · Во время планирования по модулю расписания, требующие более заданного числа регистров, отвергаются. · Планирование по модулю совмещается с распределением регистров, и spill-код (если он необходим) планируется вместе с командами исходного цикла. Хотя spill-код снижает производительность, этот подход может быть предпочтительнее других, если оптимальное расписание требует значительно больше регистров, чем имеется в наличии. · Контроль дефицита регистров до начала планирования: граф зависимостей дополняется дугами антизависимостей (с некоторыми значениями дистанций) таким образом, что в любом расписании число одновременно открытых интервалов жизни не превысит ранее заданного значения. Применение этих подходов гарантирует, что во время распределения регистров эффективность не будет снижена из-за добавления spill-кода. Конвейеризация циклов позволяет совмещать выполнение команд, относящихся к разным итерациям цикла, что значительно повышает производительность кода, поскольку именно в циклах затрачивается основное время выполнения программы. В современных промышленных компиляторах для программной конвейеризации циклов применяются преимущественно эвристические алгоритмы на основе методов планирования по модулю. Эти методы могут быть применены к достаточно широкому классу циклов, включая циклы, состоящие из нескольких базовых блоков, а также циклы с неизвестным заранее числом повторений. Экспериментальные результаты показывают, что для архитектур с высокой степенью параллелизма на уровне команд с достаточным числом регистров и без сложных ограничений по ресурсам обеспечивается эффективность кода, получаемого эвристическими алгоритмами планирования по модулю, близкая к оптимальной (получаемой при использовании точных методов). В современных встроенных системах, как правило, применяются архитектуры с ограниченными аппаратными средствами, которые имеют невысокую степень параллелизма, относительно небольшие регистровые файлы, сложные зависимости между командами по использованию ресурсов. Эти особенности связаны с необходимостью экономии накристального пространства и снижения энергопотребления, чтобы свести к минимуму выделение тепла при функционировании устройств. По результатам ряда исследований, для подобных архитектур код, генерируемый эвристическими алгоритмами планирования по модулю, в большинстве случаев оказывается далеким от оптимального. Задача конвейеризации усложняется также наличием сложных циклических зависимостей по данным. Когда первостепенное значение имеет эффективность прикладной программы и существуют ограничения на размер кода, а время компиляции не играет принципиальной роли, целесообразным представляется применение более трудоемких точных методов для поиска оптимального решения, таких как полный перебор методом динамического программирования или ЦЛП. В области конвейеризации циклов актуальным и практически значимым направлением исследований является разработка допускающих в большинстве случаев эффективное решение ЦЛП-формулировок задачи конвейеризации с ограничениями по числу требуемых регистров. Недостаточно исследованной областью остаются также методы распределения регистров в конвейеризованных циклах для архитектур с ограниченными аппаратными средствами (отсутствие ротации регистрового файла и низкая степень параллелизма, не позволяющая использовать пересылки регистров без потери производительности). Перспективной сферой исследований представляется проблема конвейеризации гнезд циклов, в частности, обобщение ЦЛП-подхода для планирования гнезд вложенных циклов. Список литературы 1. Ruttenberg J., Gao G.R., Stoutchinin A., and Lichtenstein W. Software Pipelining Showdown: Optimal vs. Heuristic Methods in a Production Compiler. In Conference on Programming Language Design and Implementation, Philadelphia, PA, pp. 1–1, 1996. 2. Ning Q., Gao G.R. A novel framework of register allocation for software pipelining. Twentieth Annual ACM SIFPLAN-SIGACT Symposium on Principles of Programmimg Languages, pp. 29–42, 1993. 3. Govindarajan R., Altman E.R., Gao G.R. A Framework for Resource-Constrained Rate-Optimal Software Pipelining. IEEE Transations on Parallel and Distributed Systems, Vol. 7, No. 11, 1996. 4. Altman E.R., Govindarajan R., Gao G.R. Scheduling and Mapping: Software Pipelining in the Presence of Structural Hazards. In Proceedings of the ACM SIGPLAN'95 Conference on Programming Language Design and Implementation, pр. 139–155, 1995. 5. Eichenberger A. Modulo Scheduling, Machine Representations, and Register-Sensitive Algorithms. The University of Michigan. Thesis. 1997. 6. Altman E.R. Optimal Software Pipelining with Function Unit and Register Constraints. PhD Thesis. Department of Electrical Engineering, McHill University, Montreal, Canada, 1995. 7. Lelait S., Gao G.R., Eisenbeis C. A New Fast Algorithm for Optimal Register Allocation in Modulo Scheduled Loops. Proceedings of the 7th International Conference on Compiler Construction, pp. 204–218, 1998.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1601 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
| Статья опубликована в выпуске журнала № 4 за 2008 год. | |
| Статья относится к отраслям: Вычисления | |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Компьютерная интеграция и интеллектуализация производств на основе их унифицированных моделей
- О моделировании данных
- Автоматизированное рабочее место расчета стоимости эксплуатации кораблей
- О программной реализации геоинформационных систем
- Учет когнитивных и поведенческих особенностей человека-эксперта при построении систем искусственного интеллекта
Назад, к списку статей



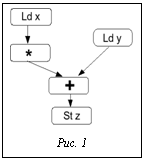 На рисунке 1 показан граф зависимостей по данным для этого цикла. Расписание одной итерации (для процессора, который может запускать до трех команд на такт и выполнять операцию умножения за 4 такта, а остальные операции за 1 такт) выглядит следующим образом:
На рисунке 1 показан граф зависимостей по данным для этого цикла. Расписание одной итерации (для процессора, который может запускать до трех команд на такт и выполнять операцию умножения за 4 такта, а остальные операции за 1 такт) выглядит следующим образом: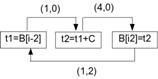
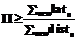 , (2)
, (2)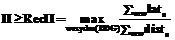 , где cycles(DDG) – множество контуров DDG. Граф зависимостей на рисунке 3 имеет один контур с суммарной латентностью 6 и суммарной дистанцией 2, то есть для этого цикла значение RecMII равно 3.
, где cycles(DDG) – множество контуров DDG. Граф зависимостей на рисунке 3 имеет один контур с суммарной латентностью 6 и суммарной дистанцией 2, то есть для этого цикла значение RecMII равно 3.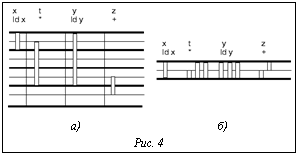 Игнорирование ложных зависимостей по регистрам при конвейеризации циклов позволяет строить значительно более эффективные расписания с глубоким перекрытием итераций, но приводит к тому, что интервалы жизни некоторых переменных могут превышать величину II. На рисунке 4 можно видеть, что интервалы жизни значений t и y превышают II=2. Для хранения таких значений необходимо выделить более одного физического регистра. (Число физических регистров, требуемых для переменной, называется размером буфера и равно éLv/IIù, где Lv – длительность интервала жизни значения.) Ряд процессоров предоставляют аппаратные средства (ротация регистрового файла), которые обеспечивают такую возможность. В отсутствие аппаратных средств используются следующие программные решения.
Игнорирование ложных зависимостей по регистрам при конвейеризации циклов позволяет строить значительно более эффективные расписания с глубоким перекрытием итераций, но приводит к тому, что интервалы жизни некоторых переменных могут превышать величину II. На рисунке 4 можно видеть, что интервалы жизни значений t и y превышают II=2. Для хранения таких значений необходимо выделить более одного физического регистра. (Число физических регистров, требуемых для переменной, называется размером буфера и равно éLv/IIù, где Lv – длительность интервала жизни значения.) Ряд процессоров предоставляют аппаратные средства (ротация регистрового файла), которые обеспечивают такую возможность. В отсутствие аппаратных средств используются следующие программные решения.