Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Генетическая настройка цифрового регулятора частоты вращения с двухрежимной фильтрацией
Аннотация:
Abstract:
| Автор: Калугин Ф.В. () - | |
| Ключевые слова: коленчатый вал, генетический алгоритм, настройка пид-регулятора, двухрежимный фильтр |
|
| Keywords: , generic algorithm, , |
|
| Всего комментариев: 1 Количество просмотров: 14597 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
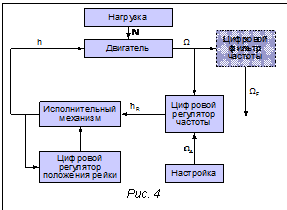
Необходимость обеспечения устойчивости холостого хода автомобильных дизелей, оснащенных электронными системами управления, обусловливает создание специальных систем управления (СУ). Данная проблема решалась и при доводке электронной системы ЭСУ-1 на дизелях серий КАМАЗ-740.60-360, КАМАЗ-740.61-320, КАМАЗ-740.62-280, поскольку двухкаскадный пропорционально-интегрально дифференциальный (ПИД) регулятор автоматически не обеспечивал устойчивую работу дизеля при отключении нагрузки [1]. Алгоритмы управления получаются более эффективными, если вместо специальной СУ холостого хода применять универсальные, то есть обеспечивающие устойчивую работу дизеля на всех нагрузочно-скоростных режимах, включая и режимы холостого хода, и торможения двигателем. В настоящей работе данная проблема решается введением модифицированного цифрового фильтра оборотов частоты [2] с переменной структурой и универсальной генетической настройкой ПИД-регулятора. Система управления дизельным двигателем Принципиальная схема регулирования частоты вращения коленчатого вала показана на рисунке 1. Текущая частота вращения W определяется величиной подачи топлива (положение рейки топливного насоса h), свойствами двигателя и нагрузкой (момент инерции нагрузки, момент сил внешнего сопротивления M2), факторами окружающей среды. Измеряемое значение W подается на вход фильтра высокой частоты, затем отфильтрованная частота вращения WF передается в качестве входного сигнала в цифровой регулятор частоты вращения двигателя. Фильтр высокой частоты может отсутствовать в контуре управления двигателем. Цифровой регулятор задает требуемое положение рейки hR для обеспечения стабильности скоростного режима, который определяется настройкой задаваемой частоты вращения WS. Исполнительный механизм (ИМ) устанавливает физическое положение рейки h, близкое к задаваемому значению hR. Текущая величина h отличается от hR вследствие инерции ИМ. Для стабилизации параметра h в ИМ используется обратная связь с цифровым регулятором положения рейки. Модификация цифрового двухрежимного фильтра оборотов частоты заключается в том, что не допускается большое отклонение отфильтрованного сигнала от реального: при разнице отфильтрованного сигнала от реального больше некоторого порога, характерного для двигателя, в качестве результата берется реальная частота. Математическая модель системы регулирования Уравнение частоты вращения двигателя имеет вид: где J – суммарный момент инерции двигателя и нагрузки, приведенной к коленчатому валу; t – время;
где M1 – крутящий момент; M2 – момент сил внешнего сопротивления; M3 – момент сил внутреннего трения. Мгновенное значение крутящего момента можно представить в виде:
где kg – коэффициент пропорциональности. С учетом (4) формула (3) принимает следующий вид:
где K1 – коэффициент пропорциональности крутящего момента к координате рейки; t1 – запаздывание (время, необходимое на движение и сгорание топлива). Предположим, что момент сил внутреннего трения пропорционален частоте вращения С учетом (2)–(5) уравнение момента импульса (1) принимает вид:
Уравнение регулятора частоты вращения Для регулирования частоты оборотов W используем классический ПИД-регулятор
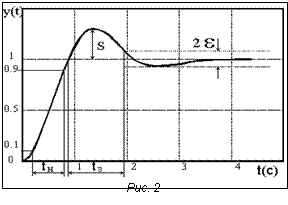
где нижний индекс k соответствует характеристике в момент времени Прямое численное моделирование системы регулирования частоты вращения На основе уравнений (6) и (7) строим систему уравнений, которая описывает замкнутую систему, состоящую из двигателя и регулятора (рис. 1). Эта система при единичном скачке на входе определяет кривую переходного процесса в системе. Численное моделирование проводим следующим образом: 1) устанавливаем первые W1…Wk-1 и Y1... 2) вычисляем частоту на k-м шаге 3) вычисляем положение рейки на шаге k+1, 4) вычисляем приращение частоты на k-м шаге 5) 6) увеличиваем шаг k, переходим к пункту 2. Вследствие наложения на работу двигателя его физических характеристик (например, задано количество цилиндров) получается более сложный периодический сигнал с повторяющимся периодом в 264 зубца. Эти данные также учитываются при моделировании – они суммируются с вычисляемой частотой WS в пункте 2. Оценка качества переходного процесса Для оценки используем 4 параметра [4] (вид переходной характеристики и ее параметров изображен на рисунке 2): 1) tH – время нарастания, то есть время, за которое переменная y(t) возрастает с 0,1 до 0,9 установившегося значения; 2) S – «выброс» (максимальное превышение сигналом y(t) единичного уровня); 3) tЗ – время затухания переходного процесса (время между моментом первого достижения сигналом y(t) единичного уровня и моментом, начиная с которого значения y(t) остаются внутри интервала [1±e]; e – некоторая постоянная); 4) Df – среднеквадратичное отклонение от задаваемого сигнала, рассчитывается на отрезке затухания переходного процесса. Первые 3 параметра являются стандартными для данной задачи. Автор статьи вводит четвертый параметр в силу использования данных о циклической неравномерности сигнала, обусловленной физическими характеристиками двигателя и моделирования флуктуационной составляющей. Оценка переходной кривой по упомянутым выше параметрам (tH, S, tЗ, Df) представляет собой многокритериальную задачу. Для ее решения воспользуемся предложенным Р. Беллманом и Л. Заде методом слияния целей и ограничений [5]. Введем лингвистические переменные «время нарастания», «время затухания», «выброс», «равномерность затухания» и определим на каждой из них терм «приемлемое значение» как нечеткое множество с функцией принадлежности m(x) трапецеидального вида. Пример функции принадлежности для терма «приемлемое значение» лингвистической переменной «выброс» приведен на рисунке 3. Конкретные значения параметров переходной кривой
Заданы следующие степени принадлежности:
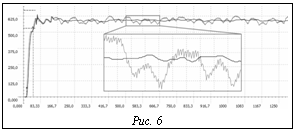
Исследуя работу реального фильтра частоты вращения, оценим переходный процесс при установлении величины частоты оборотов W, равной 600 об/cек. Сигнал, снимаемый с двигателя, отфильтровываем от шумов и периодической составляющей, для этого в систему вне контура управления добавляем цифровой фильтр частоты, как это показано на принципиальной схеме (рис. 4). Необходимо автоматизировать поиск оптимальных настроек ПИД-регулятора. Схема поиска оптимальной кривой переходного процесса Для поиска оптимальных настроек, на которых оценочная функция (8) достигает максимума, необходимо уметь оценивать переходный процесс для определенных численных настроек 1) эксперт задает функции принадлежности терма «приемлемое значение» для параметров tH, S, tЗ, Df; 2) устанавливаются начальные величины коэффициентов регулятора 3) вводятся случайные значения поправок к начальным величинам коэффициентов (DKP, DKI, DKD); 4) вычисляются новые значения коэффициентов 5) производится численное моделирование системы регулирования частоты вращения с коэффициентами, полученными в п. 4, при этом получается переходная характеристика, отображенная на рисунке 2; 6) вычисляются значения параметров 7) вычисляется степень принадлежности μ(x) каждого из параметров к нечеткому множеству «приемлемое значение» соответствующей лингвистической переменной; 8) вычисляется общая оценка переходной кривой по выражению (8); 9) Генетический подход В качестве эффективного метода нахождения оптимальных значений коэффициентов регулятора используем генетический подход. Генетические алгоритмы (ГА) – это поисковая техника, имитирующая законы природной селекции и генети- ки [6]. ГА не касается проблема локального максимума. Упрощенно схема ГА выглядит следующим образом: 1) на протяжении k-й итерации сохраняем популяцию потенциальных решений (хромосом) 2) каждое решение 3) формируем k+1 поколение методом селекции решений в соответствии с мерой пригодности – каждое решение 4) некоторые решения из следующего поколения подвергаем действию генетических операторов (кроссовера и мутации) для образования новых решений [7]; 5) алгоритм завершает работу при достижении заданных значений пригодности либо по исчерпании числа поколений. При исследованиях используем модификацию ГА, которая сохраняет наилучшее решение [8]. Результат применения генетического подхода В результате эксперимента при генетической настройке регулятора без применения фильтра частоты внутри контура управления и без учета флуктуационной составляющей были получены следующие параметры пропорционально-дифференциального регулятора: KP=7,74, KI=0, KD=0,14. Неравномерность сигнала, зависящая от цикловой подачи топлива (так называемые горбы с периодом 88 тактов), «срезана». Это отрицательно влияет на работу двигателя – происходит более быстрый его износ. В результате эксперимента при генетической настройке регулятора с применением фильтра частоты внутри контура управления и без учета флуктуационной составляющей были получены следующие параметры пропорционально-дифференциального регулятора: KP=5,4, KI=0, KD=0. Данные о неравномерности сигнала, зависящие от цикловой подачи топлива, «не срезаны». Это положительно влияет на работу двигателя – более оптимально регулируется рабочая частота оборотов коленчатого вала. На рисунке 5 показан результат переходного процесса при генетической настройке регулятора без применения фильтра частоты внутри контура управления и с флуктуационной составляющей. Получили ПИД-регулятор с параметрами KP=10,01, KI=2,81, KD=0,12. Недостатки те же, что и без флуктуационной составляющей. На рисунке 6 показан результат переходного процесса при генетической настройке регулятора с применением фильтра частоты внутри контура управления и с флуктуационной составляющей. Получен ПИД-регулятор с параметрами KP=14,12, KI=1,33, KD=0,07.
1. Хрящев Ю.Е., Кирик В.В., Третьяков А.А Использование аппарата fuzzy-логики в управлении дизелем // Математические методы в технике и технологиях: сб. тр. XX междунар. науч. конф. Ярославль: Изд-во ЯГТУ, 2007. С. 310–312. 2. Калугин Ф.В. Двухрежимный алгоритм фильтрации частоты оборотов коленчатого вала дизельного двигателя // Мехатроника, Автоматизация, Управление. 2008. № 5. С. 35–41. 3. Крутов В.И. Автоматическое регулирование двигателей внутреннего сгорания. М.: Машиностроение, 1979. С. 616. 4. Денисенко В. ПИД-регуляторы: принципы построения и модификации // Современные технологии автоматизации. 2006. № 4. С. 66–74. 5. Giuseppe Munda. Multicriteria evaluation in a fuzzy environment. Physica-Verlag, 1995. 6. Chuck Karr. Genetic Algorithms for Fuzzy Controllers, AI Expert, 1991, Febriary, pp. 25–32. 7. Kim Chwee Ng, Yun Li. Design of Sophisticated Fuzzy Logic Controller Using Genetic Algorithms Proc. 3rd IEEE Int. Conf. On Fuzzy Systems, Orlando, FL, June, 1994. Vol. 3, pp. 1708–1712. 8. Goldberg D.E. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, 1989. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2246 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. | Версия для печати с комментариями |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Генетический алгоритм автоматизированного проектирования подготовительных переходов ковки
- Интеллектуальная система прогнозирования на основе методов искусственного интеллекта и статистики
- Программный комплекс решения задачи кластеризации
- Программа параметрического синтеза гибких производственных систем
- Исследование эффективности бионических алгоритмов комбинаторной оптимизации
Назад, к списку статей
Comments
автор: Виктория [2009-08-19 14:20:07]Оценка пользователя: 10 баллов



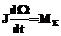 , (1)
, (1)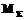 – суммарный момент приложенных сил.
– суммарный момент приложенных сил. 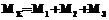 , (2)
, (2) , (3)
, (3)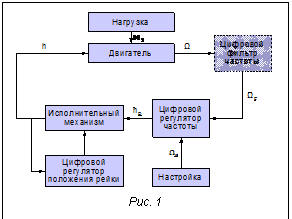 где Hu – теплотворная способность топлива; id – число цилиндров в двигателе; td – тактность двигателя; gc – цикловая подача топлива; he – эффективный КПД; M¢(t) – флуктуационная составляющая (шум двигателя), среднее по времени значение M¢(t) равно нулю [3]. Цикловая подача топлива зависит от частоты вращения W и координаты рейки топливного насоса h. В первом приближении будем считать gc пропорциональной координате рейки и не зависящей от частоты:
где Hu – теплотворная способность топлива; id – число цилиндров в двигателе; td – тактность двигателя; gc – цикловая подача топлива; he – эффективный КПД; M¢(t) – флуктуационная составляющая (шум двигателя), среднее по времени значение M¢(t) равно нулю [3]. Цикловая подача топлива зависит от частоты вращения W и координаты рейки топливного насоса h. В первом приближении будем считать gc пропорциональной координате рейки и не зависящей от частоты: , (4)
, (4) , (5)
, (5)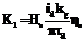 ,
,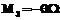 , где q – коэффициент сопротивления.
, где q – коэффициент сопротивления. . (6)
. (6) , (7)
, (7) ; Dt – шаг квантования по времени; KP, KI, KD – постоянные времени регулятора (пропорциональная, интегральная и дифференциальная);
; Dt – шаг квантования по времени; KP, KI, KD – постоянные времени регулятора (пропорциональная, интегральная и дифференциальная); 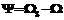 , где WS – задаваемая угловая скорость (частота).
, где WS – задаваемая угловая скорость (частота). , равные 0, где
, равные 0, где  ;
; ;
;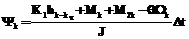 , где в качестве Mk берем случайные величины в интервале [–2, 2];
, где в качестве Mk берем случайные величины в интервале [–2, 2];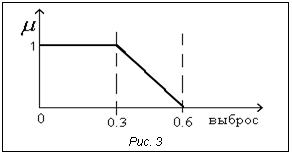 так как задачей нашего исследования является имитация условий холостого хода, Mk=0 (внешняя нагрузка отключена);
так как задачей нашего исследования является имитация условий холостого хода, Mk=0 (внешняя нагрузка отключена); (tH, S, tЗ, Df) могут быть охарактеризованы степенью принадлежности m(x) каждого из параметров к терму «приемлемое значение» соответствующей лингвистической переменной. В рассматриваемом случае представляется естественным принять в качестве оценки переходного процесса
(tH, S, tЗ, Df) могут быть охарактеризованы степенью принадлежности m(x) каждого из параметров к терму «приемлемое значение» соответствующей лингвистической переменной. В рассматриваемом случае представляется естественным принять в качестве оценки переходного процесса . (8)
. (8) ,
,
 ,
,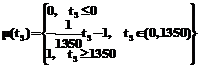 ,
, .
.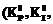
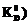 ПИД-регулятора. Схема поиска оптимальной кривой переходного процесса выглядит следующим образом [4]:
ПИД-регулятора. Схема поиска оптимальной кривой переходного процесса выглядит следующим образом [4]: ;
;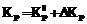 ,
,  ,
, 
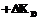 ;
; если вычисленная оценка в п. 8 является максимальной, то алгоритм останавливается, иначе повторяется процедура для новых значений
если вычисленная оценка в п. 8 является максимальной, то алгоритм останавливается, иначе повторяется процедура для новых значений  , в начальный момент времени можно наполнить 1-ю популяцию любыми пригодными значениями; отдельной хромосомой
, в начальный момент времени можно наполнить 1-ю популяцию любыми пригодными значениями; отдельной хромосомой 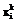 является набор коэффициентов ПИД-регулятора
является набор коэффициентов ПИД-регулятора  по выражению (8);
по выражению (8); ;
; В заключение следует отметить, что в результате проведенных исследований, связанных с применением ГА, были найдены оптимальные настройки ПИД-регулятора для регулирования частоты оборотов коленчатого вала. Модифицированный двухрежимный алгоритм фильтрации частоты оборотов коленчатого вала дизельного двигателя [1] показал свою пригодность для включения в контур управления оборотами дизельного двигателя.
В заключение следует отметить, что в результате проведенных исследований, связанных с применением ГА, были найдены оптимальные настройки ПИД-регулятора для регулирования частоты оборотов коленчатого вала. Модифицированный двухрежимный алгоритм фильтрации частоты оборотов коленчатого вала дизельного двигателя [1] показал свою пригодность для включения в контур управления оборотами дизельного двигателя.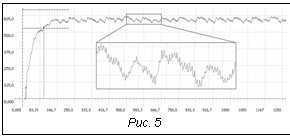 Литература
Литература