Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Автоматическое планирование с использованием фокусировки
Аннотация:
Abstract:
| Автор: Трофимов И.В. () - | |
| Ключевые слова: планировщик, фокусировка, абстрагирование, автоматическое планирование |
|
| Keywords: , , abstraction, |
|
| Количество просмотров: 10645 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
Традиционно в литературе по искусственному интеллекту абстрагирование определяется как частный случай изменения способа представления. По мнению современных исследователей проблемы абстрагирования [1], сложно дать понятию «абстрагирование» точную формулировку, достаточно общую, чтобы включать все разнообразие методов, интуитивно подпадающих под эту категорию, и в то же время достаточно специфичную, чтобы исключить другие формы изменения способа представления, интуитивно абстрагированием не являющиеся (например переформулировка). Мы будем придерживаться определения, предложенного Зюкером [2]. Методы абстрагирования можно классифицировать по механизму, который используется для скрытия несущественных деталей. По мнению автора, таких механизмов два. 1. Скрытие элементов предметной области. В качестве элементов могут выступать объекты, процессы, явления, действия и т.д. В литературе такой механизм называют фокусировкой, или скрытием домена, или проекцией. 2. Скрытие свойств элементов предметной области. Скрытие свойств может сделать отдельные элементы домена неразличимыми (уменьшается разнообразие), но количество элементов не изменяется. Скрытие свойств может выполняться не для всех элементов домена, а только для определенных групп или даже отдельных элементов. В литературе этот механизм называют также избирательностью, или скрытием содомена, или абстрагированием домена. Абстрагирование в планировании Существует множество планировщиков, использующих абстрагирование, в которых можно выделить общую методологическую основу: сначала осуществляется переход к абстрактной формулировке задачи, затем решается абстрактная задача, сложность которой меньше сложности исходной задачи, и, наконец, на базе абстрактного решения отыскивается решение исходной задачи. Абстрагирование формулировки задачи в большинстве работ сводится к синтаксическому удалению элементов предусловия действий (типично – элементов конъюнкции в предусловиях, выраженных в форме конъюнкции литералов). К числу таких планировщиков относятся системы ABSTRIPS, ABTWEAK, PRODIGY/ALPINE. Абстрагирование также можно выполнять путем синтаксического удаления элементов эффекта действий. Этот принцип используют планировщики HSP и FF. Что касается применения абстрактного решения, то здесь существуют два основных метода. Первый заключается в том, что длина абстрактного решения используется как эвристическая оценка расстояния до цели. На базе этого метода реализованы планировщики HSP и FF. Во втором методе само абстрактное решение выступает в качестве каркаса искомого решения, и необходимо найти лишь подходящую ему конкретизацию. На базе этого метода реализованы планировщики ABSTRIPS, ABTWEAK, PRODIGY/ALPINE. Для второго подхода важным условием является возможность создания эффективного алгоритма конкретизации абстрактного решения. При определенных ограничениях это условие выполняется. Однако если оно не выполняется, такой подход может оказаться гораздо менее эффективным, чем методы, не использующие абстрагирование. Все упомянутые планировщики осуществляют абстрагирование путем скрытия свойств элементов предметной области, а именно, свойств действий. Однако не менее полезным для поиска решения проблемы вычислительной сложности является скрытие самих элементов предметной области (фокусировка) – объектов и действий, которые не могут иметь отношение к решению текущей задачи. Отсев нерелевантных объектов и действий может в значительной мере сокращать пространство поиска. Кроме того, важным свойством фокусировки является то, что абстрактное решение – это также и конкретное решение, поэтому нет необходимости в конкретизации. Автору неизвестны планировщики, осуществляющие абстрагирование таким способом. Модель фокусировки для задачи планирования Определимся с формализацией задачи планирования и механизма абстрагирования. Обозначим Schemas конечное множество схем действий, описывающих все возможные виды деятельности для данного агента. Каждому элементу множества Schemas соответствует целое неотрицательное число k, обозначающее количество объектов, вовлеченных в описание действий, соответствующих данной схеме. Назовем это число арностью схемы действий, или количеством параметров схемы действий. Арность схемы действий удобно моделировать при помощи функции h: Schemas → Z+. На письме для обозначения арности схемы действий используется верхний индекс. Например, запись schemak означает, что речь идет о такой schema, для которой h(schema) = k. Каждому описанию схемы действий соответствует непустое множество описаний конкретных действий. Описание действия представляет собой кортеж вида: ‹schemak, obj1,…, objk›, где obji – имена объектов, вовлеченных в описание действия. Способы формирования описаний конкретных действий из схем могут быть различными. Множество всех действий, соответствующих некоторой схеме действий schema, обозначим actions[schema], а множество всех возможных действий агента – Actions. Actions = Во всякий момент внешняя среда находится в каком-либо состоянии. Множество всех возможных состояний, в которых может пребывать внешняя среда, обозначим States. Для каждого состояния в States определено множество действий из Actions, которые выполнимы в данном состоянии. Другими словами, существует функция g: Actions×States→{выполнимо, невыполнимо}, которая для каждого действия из Actions и каждого состояния среды из States определяет, выполнимо ли действие в данном состоянии. Функция g – функция выполнимости. Выполнение всякого действия приводит к изменению состояния среды. Обозначим AS множество всех пар ‹action, state› (actionÎActions, stateÎStates), для которых выполняется условие (xÎAS→(g(x)=выполнимо)). Определим функцию f: AS → States, причем, если f(action, state1)=state2, то state1¹ ¹state2; f – функция переходов. Определим задачу планирования как кортеж вида ‹States, Actions, g, f, S0, SG›, где S0ÎStates – начальное состояние; SGÌStates – множество состояний, являющихся целевыми для данной задачи планирования (в этих состояниях выполняется целевое условие); S0ÏSG. Решением задачи планирования (или планом) назовем последовательность вида ‹S0, A0, S1, A1, …, SN, AN, SN+1›, для которой выполняются следующие условия: 1. SiÎStates, AjÎActions, где 0≤i ≤N+1, 0≤j≤N; 2. SN+1ÎSG; 3. SiÏSG, где 0 ≤i≤N; 4. g(Ai, Si)=выполнимо, где 0≤i≤N; 5. f(Ai, Si)=Si+1, где 0≤i≤N. Пусть P – некоторая задача планирования, тогда Solutions(P) обозначим множество всех возможных решений задачи планирования P. Определив таким образом постановку задачи планирования и результат ее решения, перейдем к формальному определению понятия фокусировки для задачи планирования. Для данной задачи P=‹States, Actions, g, f, S0, SG› результатом фокусировки будет абстрактная задача P1=‹States1, Actions1, g, f, S0, SG1›, отвечающая следующим требованиям: 1. States1ÍStates; 2. Actions1ÍActions; 3. aÎActions1, sÎStates1, g(a, s)=выполнимо → f(a,s)ÎStates1; 4. SG1ÌStates1; 5. SG1ÍSG; 6. Solutions(P1)ÍSolutions(P); 7. |Solutions(P)|¹0 → |Solutions(P1)|¹0. Предложенная модель фокусировки предполагает, что абстрактная задача отличается от исходной содержанием множеств состояний, действий, целевых состояний. В данной работе рассматривается механизм фокусировки, сокращающий только множество Actions, то есть предполагается выполнение условий States1=States, SG1=SG и Actions1ÌActions. Согласно требованию 7, если существует решение исходной задачи, то множество Actions1 должно содержать набор действий, из которых можно получить хотя бы одно решение абстрактной задачи. Это абстрактное множество действий назовем значимым контекстом и обозначим SCx. Исключенные (абстрагированные) действия составляют множество, которое назовем допустимым незначимым контекстом и обозначим NCx. Эти два вида контекстов связаны соотношением SCx=Actions\NCx. Таким образом, чтобы осуществить абстрагирование, нам достаточно найти либо значимый контекст, либо допустимый незначимый контекст. Чтобы воспользоваться предложенным механизмом абстрагирования, необходимо решить две подзадачи: найти адекватное средство определения для контекстов и механизм выявления NCx или SCx для текущей задачи планирования. Способы определения контекстов По определению, значимый и допустимый незначимый контексты являются множествами. Есть два основных способа определения множеств – перечисление элементов и определение посредством характеристического свойства. Рассмотрим второй способ. В общем виде определение контекста Cx посредством характеристического свойства можно записать следующим образом: Cx={a | aÎActions, filter}, где filter – требование к элементам Cx (характеристическое свойство). То есть контекст представляет собой такое множество элементов из Actions, которые отвечают требованию filter. В силу того что действие моделируется как составная сущность, а именно как кортеж вида ‹schemak, obj1,…, objk›, можно накладывать ограничения на элементы, из которых состоит действие. Во-первых, можно потребовать, чтобы элементами контекста были действия, порожденные от одной определенной схемы действий: Cx={a | aÎActions, aÎactions[schema]}, где schemaÎSchemas. Во-вторых, требование может постулировать, что n-м параметром действия является имя конкретного объекта Obj. Обозначим actionsi,Obj[schemak] множество действий, порожденных от схемы schemak, у которых в качестве i-го параметра (и, следовательно, i+1-го элемента кортежа, описывающего действие) выступает имя объекта Obj (здесь 1≤i≤k). Тогда множеством всех действий, у которых i-й параметр равен Obj, является объединение множеств actionsi,Obj[schemak] по всем схемам действий с арностью, большей либо равной i. Обозначим это множество actionsi,Obj: actionsi,Obj= Соответственно, контекст будет определяться как Cx={a | aÎActions, aÎactionsi,Obj}. Разумеется, в качестве требования может выступать и принадлежность или непринадлежность a множеству actionsi,Obj[schemak]. В-третьих, можно сформулировать требование, согласно которому контекст состоит из действий, оперирующих объектом Obj. Множество таких действий будем обозначать actionsObj: actionsObj= Определение соответствующего контекста: Cx={a | aÎActions, aÎactionsObj}. Такое условие определяет, что все действия, составляющие контекст, должны оперировать объектом Obj. Для значимого контекста требование непринадлежности такому множеству фактически исключает объект из рассмотрения. То есть требование SCx = {a | aÎActions, aÏactionsObj} в действительности постулирует абстрагирование от одного определенного объекта предметной области (посредством абстрагирования от операций с ним). В-четвертых, требование может ограничить контекст действиями, оперирующими объектом Obj и, кроме того, порожденными от одной конкретной схемы (а не от любой, как в предыдущем случае). Множество таких действий обозначим actionsObj[schemak]: actionsObj[schemak]= Соответствующее определение контекста: Cx={a | aÎActions, aÎactionsObj[schemak]}. Так как характеристическое свойство задано посредством операции принадлежности или непринадлежности какому-либо множеству, можно строить из предложенных множеств (а также из индивидуальных действий) более сложные требования к контексту, используя операции над множествами. Способ задания контекста посредством характеристического свойства достаточно гибок. Переходя к более сложным моделям задачи планирования, можно составлять характеристические требования другого рода – оперирующие понятиями новой модели. Например, если рассматривать действия как сущности, обладающие предусловием и эффектом (именно так обычно определяются действия в планировании), то можно ввести ограничения и на эти элементы. Кроме этого, оперируя объектами, можно осуществлять отбор по их характеристикам. Выявление значимого контекста на базе правил Гибким способом выявления значимого контекста является создание эвристик, опирающихся на набор декларативных правил, которые определяют связь между формальной постановкой задачи и контекстом. Декларативное представление знаний позволяет без изменения алгоритмов настраивать планировщик на работу с новыми предметными областями и задачами. Такой подход предполагает наличие единого механизма интерпретации правил, а значит, и наличие некоторого формального языка описания правил. Рассмотрим один из языков такого рода, названный языком декларации принципа абстрагирования (ЯДПА). ЯДПА – язык сценариев. Значимый контекст выявляется при помощи выполнения инструкций и операций. Инструкции отвечают за управление последовательностью выполнения операций и именование результатов операций. Операции формируют значимый контекст, а также промежуточные вспомогательные множества. ЯДПА содержит три инструкции: условие, переход и присваивание. Инструкция «условие» имеет вид Если (идентификатор) инструкция и интерпретируется следующим образом. Если соответствующее идентификатору множество не пусто, выполняется инструкция после скобок. Инструкция «переход» имеет вид Переход метка_перехода. Интерпретация данной инструкции: следующей будет выполнена инструкция, помеченная меткой перехода. Инструкция «присваивание» имеет вид идентификатор = операция. Ее интерпретация: полученное в результате выполнения операции множество будет иметь имя, заданное идентификатором. Выполнение операций всегда связано с инструкцией присваивания. Инструкции должны формировать сценарий таким образом, чтобы всякая последовательность выполнения операций приводила к формированию специального множества с именем SCx, соответствующего значимому контексту. Инструкции «условие» и «переход» позволяют реализовать операцию транзитивного замыкания при построении множеств, а также осуществлять классификацию задач планирования. Операции ЯДПА содержательно идентичны операциям реляционной алгебры. В язык включены операции выборки, проекции, декартова произведения, объединения, пересечения и разности. Дополнительно введены еще две операции: выборка одного произвольного элемента и (реляционная) группировка с выборкой одного произвольного элемента в каждой группе. Операции можно выполнять над так называемыми базовыми множествами или множествами, полученными при помощи ранее выполненных операций. Базовыми считаются следующие множества. · Множество всех объектов (Objects) из постановки задачи планирования. Элементами этого множества являются кортежи из двух элементов <имя объекта, непосредственный тип объекта>. · Множество всех конкретизированных действий (Actions) задачи планирования. Это множество состоит из кортежей, длина которых больше максимальной арности схем на единицу. Первый элемент кортежа содержит имя действия, остальные – аргументы (если количество аргументов у действия меньше длины кортежа, оставшиеся элементы кортежа принимают специальное значение «пусто»). Результирующее множество SCx должно являться подмножеством Actions. · Для каждого предиката P арности k в определении домена существует пара множеств InInit_P и InGoal_P, элементами которых могут быть кортежи длины k. Элементами данных множеств являются кортежи имен объектов. Если начальное состояние задачи содержит атомарную формулу, производную от P, аргументы этой формулы составляют кортеж, который является элементом InInit_P. Аналогично для цели задачи. Такая формулировка налагает ограничение на спектр задач, к которым может быть применен метод – начальное состояние и цель задачи планирования должны определяться списком атомарных формул (или их конъюнкцией). Все базовые множества могут быть построены автоматическими средствами на основании формулировки задачи планирования. Элементы кортежей именованы. В Objects первый элемент именуется obj, второй – type. В Actions первый элемент именуется aName, остальные – arg1, arg2, …, argN, где N – максимальная арность схем действий. Во множествах вида InInit_P и InGoal_P элементам кортежей присваиваются имена аргументов предиката P согласно его описанию в домене. Во всех операциях, за исключением проекции, разрешается переименование элементов кортежа, формируемого в результате выполнения операции. В качестве примера использования ЯДПА рассмотрим процесс отбора полезных действий stack из домена Blocks World. Если в цели задачи указан атом (on x, y), то действие stack(x, y) является полезным. Для получения множества всех таких действий сначала из Actions отбираются действия stack: StackActions=Выборка( | AllActions | aName=‘stack’). Затем строится декартово произведение этого множества с множеством кортежей объектов для предиката ON в цели: Stack_x_OnInGoal = ДекПроизв( | StackActions, InGoal_ON). Далее из этого множества отбираются те записи, у которых arg1=x и arg2=y: StackEx=Выборка( | Stack_x_OnInGoal | arg1=x, arg2=y). Формируется окончательное множество действий stack (без лишних столбцов): FinalStack=Проекция( | StackEx). Результаты экспериментов Чтобы убедиться в жизнеспособности подхода, были проведены эксперименты, в ходе которых оценивались следующие показатели: количество решенных задач, время поиска плана, длина плана. Сопоставлялись показатели, полученные при помощи оригинального планировщика FF версии 2.3 [3] и этого же планировщика, дополненного модулем абстрагирования. В качестве тестовых задач взяты strips-задачи с соревнований планировщиков IPC. Эксперименты проводились на доменах Blocks World (мир блоков), Depots (склады), Satellite (спутник). Blocks World (4 оператора)
После абстрагирования значимый контекст составляли действия stack(x, y), если цель задачи содержала атом (on x, y); действия unstack(x, y), если начальное состояние задачи содержало атом (on x, y); все действия pickup и putdown. В эксперименте задача считалась нерешенной, если планировщик работал более 10 минут или тратил более 1 Гб ОЗУ. Оригинальный FF не решил 25 задач (причем 4 нерешенные задачи из основного трека). Абстрагирующий планировщик решил все задачи. Для совместно решенных задач планировщики получали планы почти одинаковой длины и (за редким исключением) схожее время работы. Depots
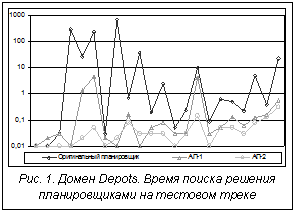
В экспериментах были опробованы два принципа абстрагирования. Первый позволял выгружать и складировать ящики только в пункте их назначения (АП-1). Второй дополнял первый принцип тем, что грузить ящики позволялось лишь в месте их изначального нахождения и допускалось использование только одного грузовика (АП-2). Результаты представлены на рисунке 1. (На рисунках 1 и 2: ось абсцисс – задачи, ось ординат (логарифмическая) – время поиска решения в секундах.) Планировщики с абстрагированием не только продемонстрировали выигрыш по времени, но и на многих задачах сгенерировали более короткие планы. Эксперимент для домена «склады» был продолжен на наборе внеконкурсных задач (22 задачи из каталога HandCoded) значительно большего размера. Для этого блока задач были выставлены лимит в 10 минут и ограничение на память в 1 Гб. Из внеконкурсных задач оригинальному планировщику удалось решить только одну (первую). АП-1 решил 8 задач; АП-2 – 12 задач. Самый длинный план был получен АП-2 на 17-й задаче – 388 шагов (за 531 сек.). Satellite Задачи состоят в планировании наблюдений для группы спутников, имеющих различное оборудование. Домен «спутник» был тестовым треком на третьем соревновании IPC. Трек состоял из 20 задач. Дополнительно в экспериментах с абстрагированием использовались 16 внеконкурсных задач (каталог HandCoded). Основу принципа абстрагирования составило ограничение множества поворотов спутников на цели и ограничение количества используемых инструментов. Инструменты выбирались по одному для каждого режима съемки, а повороты спутник осуществлял только на цели съемки, калибровки или глобальные цели задачи, указывающие окончательную ориентацию спутников. И оригинальный FF, и абстрагирующий планировщик решили все задачи. Результаты экспериментов показаны на рисунке 2. В заключение отметим: эксперименты показывают, что использование фокусировки в задачах планирования может давать значительный выигрыш по времени поиска решения за счет сокращения поискового пространства. Разработанный подход на базе правил, определяющих связь между формальной постановкой задачи и релевантными для ее решения действиями, может быть развит для поддержки широкого спектра элементов современного PDDL, что еще более усилит его дифференцирующие возможности. Предложенная модель фокусировки достаточно общая и допускает множество альтернативных путей определения и выявления значимого контекста. Литература 1. Holte R.C., Choueiry B.Y. Abstraction and reformulation in artificial intelligence // Philosophical Transactions of the Royal So- ciety B: Biological Sciences. 2003. 358(1435). pp. 1197–1204. 2. Zucker J.-D. A grounded theory of abstraction in artificial intelligence // Ibidem. 358(1435). pp. 1293–1309. 3. Hoffmann J., Nebel B. The FF Planning System: Fast Plan Generation Through Heuristic Search // Journal of Artificial Intelligence Research. 2001. № 14. pp. 253–302. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2248 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 .
.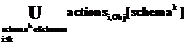 , 1≤i.
, 1≤i. .
. .
. На втором соревновании IPC в качестве тестов использовались задачи для мира кубиков. Трек состоял из 35 задач (конфигурации от 4 до 17 кубиков). Эксперимент также проводился на 67 внеконкурсных дополнительных задачах (от 17 до 50 кубиков).
На втором соревновании IPC в качестве тестов использовались задачи для мира кубиков. Трек состоял из 35 задач (конфигурации от 4 до 17 кубиков). Эксперимент также проводился на 67 внеконкурсных дополнительных задачах (от 17 до 50 кубиков).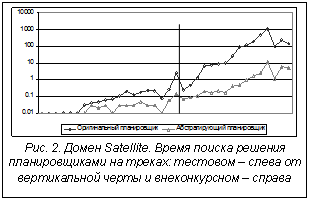 Домен «склады» является объединением хорошо известных логистического домена (Logistics) и мира кубиков. Задачи домена «склады» использовались в качестве тестов на третьем соревновании IPC. Трек состоял из 22 задач.
Домен «склады» является объединением хорошо известных логистического домена (Logistics) и мира кубиков. Задачи домена «склады» использовались в качестве тестов на третьем соревновании IPC. Трек состоял из 22 задач.