Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Метод интеллектуальной обработки медико-биологических данных
Аннотация:В работе представлен метод интеллектуальной обработки многомерных плохо формализованных массивов медико-биологической информации, базирующийся на эволюционном подходе к решению экстремальных задач функции многих переменных. Предлагаемый метод позволяет прогнозировать результаты лечения с учетом медико-биологических и социальных особенностей пациентов. Приведены результаты численного эксперимента.
Abstract:Method of intellectual processing of poorly formalized multivariable diverse arrays of biomedical information, based on evolutional method for solving of extreme tasks of multivariable function, is presented in the article. The proposed method allows predicting treatment results take account of biomedical and social features of the patients. Results of numerical experiment are adduced.
| Авторы: Цыганкова И.А. (pallada-ltd@infopro.spb.su) - Учреждение Российской академии наук Санкт-Петербургский институт информатики РАН, кандидат технических наук | |
| Ключевые слова: прогнозирование, медико-биологическая информация, эволюционный метод, обработка данных |
|
| Keywords: forecasting, the medical and biologic information, evolutionary method, data processing |
|
| Количество просмотров: 13186 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
Рост требований к качеству жизни, появление новых диагностических и лечебных технологий привели к резкому увеличению стоимости медицинских услуг. Это обострило проблему оптимизации затрат на лечение и профилактику заболеваний как для пациентов, так и для медицинских организаций различного уровня. Решить ее можно только современными методами оптимизации и прогнозирования результатов лечения, учитывающими медико-биологические и социальные особенности пациентов. Развитие вычислительной техники и информационных технологий позволяет перейти к решению задач прогнозирования в медицине с помощью интеллектуальных методов анализа данных [1–3]. Особенностями реальных медико-биологических данных являются высокая размерность и разнотипность, большое количество шумящих и дублирующих признаков, пропущенные и аномальные значения. В такой ситуации эф- фективными становятся методы, основанные на эволюционном подходе, которые, в отличие от традиционных методов поиска оптимального решения, ориентированы на наилучшее (приемлемое) решение по сравнению с полученным ранее или предложенным в качестве начального. Рассматривается задача прогнозирования результатов лечения при заданной тактике лечения на примере кожного хронического заболевания псориаз. Исходная информация о больных представлена в виде числовых таблиц «объект–свойство» с описанием входных и выходных пара- метров (признаков, характеристик) пациентов. К входным параметрам относятся индивидуальные сведения о больном: анамнез, сопутствующие заболевания, клинико-функциональные, метаболические и иммунологические показатели, тактика лечения. Выходными (целевыми) параметрами являются продолжительность пребывания пациента в стационаре (количество койко-дней), продолжительность лечения до наступления улучшения состояния (эффект лечения), продолжительность периода ремиссии, наличие (или отсутствие) типичных остаточных поражений на коже, число обострений болезни в год. Входные параметры в различной степени влияют на выходные параметры, но какие из них оказывают наиболее существенное влияние на целевые параметры и какой моделью описываются зависимости их влияния, неизвестно. В общем случае исходная информация об объектах представлена в виде матрицы
где Требуется с приемлемой точностью предсказать значения неизвестных выходных параметров нового объекта по его известным входным параметрам. Рассматриваемая задача прогнозирования является плохо формализованной в силу того, что вся информация об объектах представлена лишь набором параметров, о которых нельзя сколько-нибудь определенно сказать, что они полны, непротиворечивы и не искажены. При таких исходных данных будем использовать модель черного ящика, а при построении алгоритмов анализа данных опираться только на массивы прецедентов и гипотезу о монотонности пространства решений: «похожие входные ситуации приводят к похожим выходным реакциям системы». Решение задачи прогнозирования с помощью предлагаемого метода состоит из нескольких этапов: предобработка данных, подбор весовых параметров в процессе обучения, предсказание значений целевых параметров. Этап предобработки включает: структуризацию данных, выявление и устранение аномальных и пропущенных значений, кодировку и нормировку данных, измеряемых в непрерывных шкалах. Параметры, измеряемые в дискретных шкалах и имеющие число градаций больше двух, преобразуются в совокупность бинарных величин. Введем вектор - в выборку попадают объекты вне зависимости от значения признака - в выборку попадают объекты, для которых - в выборку попадают объекты, для которых Один и тот же объект может оказаться в нескольких выборках, которые имеют различное количество объектов. В дальнейшем используются только информативно значимые выборки, в которых количество объектов значительно больше числа количественных входных параметров. На следующем этапе (процесс обучения) для каждой информативно значимой выборки определяются веса входных параметров Каждый Так как степень гладкости функции
Значения весовых коэффициентов Чтобы обеспечить необходимую точность вычисления прогнозируемого параметра, введем критерий, который минимизирует среднюю абсолютную ошибку прогноза
Здесь Если целевая функция представляет собой комплекс выходных параметров, априори задаются коэффициенты значимости Тогда критерий (2) может быть представлен в виде
Для определения расчетных значений Итеративный процесс уточнения критерия Следующий этап решения задачи – использование полученных в процессе обучения результатов для прогнозирования искомых целевых параметров нового объекта по его известным входным характеристикам. Для этого сначала выявляются те информативные выборки, в которые попадает новый объект с учетом своих качественных признаков. Для дальнейшего анализа используется выборка, в которой ошибка прогноза имеет наименьшее значение. Расчет каждого целевого параметра нового объекта сводится к задаче экстраполяции функции После того как становятся известными выходные параметры нового объекта, объект пополняет обучающие выборки и проводится уточнение весовых коэффициентов в соответствии с изложенным методом. Таким образом, прогнозирование целевых параметров является не разовой операцией, а процессом, в ходе которого постоянно выполняются сбор, очистка и консолидация исходных данных, уточнение весовых параметров и верификация результатов. Для оценки эффективности разработанного метода прогнозирования был проведен численный эксперимент с использованием реальных медико-биологических данных больных псориазом, полученных в лечебных медицинских учреждениях Санкт-Петербурга. При проведении численного эксперимента использовался программный комплекс поддержки принятия врачебных решений, описание структуры которого приведено в рабо- те [4]. Объем исходной выборки пациентов составил 308 человек. Из них случайным образом были отобраны 45 пациентов – контрольная выборка. Общее количество числовых параметров составило 44, их них 39 – входные параметры, а 5 – выходные. Обобщенные результаты расчетных исследований по оценке прогноза целевых параметров сведены в таблицу, из которой видно, что величина средней абсолютной ошибки прогноза параметров не превышает 17 %. Результаты прогноза выходных параметров
Проведенные расчетные исследования оценки прогнозирования целевых параметров показали высокую эффективность предлагаемого метода. Величина средней абсолютной ошибки прогноза составила 10–17 %. Достоверность полученных результатов подтверждена расчетами на контрольной выборке. Разработанный метод интеллектуальной обработки многомерных разнотипных массивов медико-биологической информации позволяет подобрать весовые коэффициенты входных параметров,
Предлагаемый метод прогнозирования может использоваться в любой предметной области, где сведения об объектах сведены в информационные массивы большого объема, описываются в протоколах «вход–выход», и для них справедлива гипотеза о монотонности принятия решений в локальной области. Литература 1. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Новосибирск: Изд-во Ин-та математики, 1999. 270 с. 2. Корнеев В.В., Гареев А.Ф., Васютин С.В., Райх В.В. Базы данных. Интеллектуальная обработка информации. М.: Нолидж, 2001. 496 с. 3. Барсегян А.А., Куприянов М.С., Степаненко В.В., Холод И.И. Технологии анализа данных: Data Mining, Visual Mining, OLAP. СПб: БХВ-Петербург, 2007. 275 с. 4. Цыганкова И.А. Программный комплекс системы поддержки принятия врачебных решений // Программные продукты и системы. 2008. № 4. С. 155–158. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2339 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Адекватные междисциплинарные модели в прогнозировании временных рядов статистических данных
- Программа для определения причины схода снежной лавины
- Разработка прототипа информационно-технологического процесса обработки информации с учетом его стоимости
- Программная среда прогнозирования вероятностной надежности элементов сложных электротехнических систем
- Интеллектуальный подход к задаче информирования и краткосрочного прогнозирования временного ряда в онлайн-режиме
Назад, к списку статей



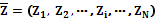 ,
, – вектор анализируемых параметров (свойств, признаков) i-го объекта. Каждый параметр
– вектор анализируемых параметров (свойств, признаков) i-го объекта. Каждый параметр  принимает значение из множества допустимых значений. Вся совокупность параметров объектов делится на входные
принимает значение из множества допустимых значений. Вся совокупность параметров объектов делится на входные  и выходные
и выходные 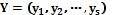 параметры. Входные параметры
параметры. Входные параметры  являются разнотипными, то есть измеряются в количественных и качественных шкалах. Обозначим через
являются разнотипными, то есть измеряются в количественных и качественных шкалах. Обозначим через  параметры, значения которых измеряются в количественных шкалах, а через
параметры, значения которых измеряются в количественных шкалах, а через  – параметры, значения которых измеряются в качественных (номинальных и порядковых) шкалах. Вектор выходных параметров
– параметры, значения которых измеряются в качественных (номинальных и порядковых) шкалах. Вектор выходных параметров  для сформулированной задачи измеряется в количественной шкале.
для сформулированной задачи измеряется в количественной шкале.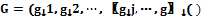 , где
, где  – бинарные признаки объектов. На этапе предобработки все множество исследуемых объектов разбивается на подмножества (выборки) в соответствии со значениями
– бинарные признаки объектов. На этапе предобработки все множество исследуемых объектов разбивается на подмножества (выборки) в соответствии со значениями 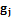 . Общее количество таких выборок составит
. Общее количество таких выборок составит  , где – количество бинарных величин;
, где – количество бинарных величин; 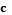 – количество вариантов (альтернатив) группировки объектов по каждому бинарному признаку . Возможны следующие варианты группировки объектов:
– количество вариантов (альтернатив) группировки объектов по каждому бинарному признаку . Возможны следующие варианты группировки объектов: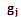 ;
; ;
;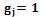 .
. . Определение весовых коэффициентов базируется на эволюционном подходе к решению экстремальных задач функции многих переменных и методе случайного поиска. Обозначим вектор весов через
. Определение весовых коэффициентов базируется на эволюционном подходе к решению экстремальных задач функции многих переменных и методе случайного поиска. Обозначим вектор весов через 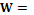 , где
, где  – весовые коэффициенты входных параметров.
– весовые коэффициенты входных параметров. объект может быть представлен в виде вектора многомерного пространства
объект может быть представлен в виде вектора многомерного пространства  количественных параметров
количественных параметров  , где
, где  – входные параметры объекта,
– входные параметры объекта,  – выходной (целевой) параметр объекта,
– выходной (целевой) параметр объекта, 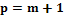 – общее количество параметров многомерного пространства. В этом случае задача определения искомого параметра
– общее количество параметров многомерного пространства. В этом случае задача определения искомого параметра  сводится к задаче интерполяции функции
сводится к задаче интерполяции функции  , заданной в узлах p-мерной нерегулярной сетки.
, заданной в узлах p-мерной нерегулярной сетки.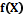 неизвестна, для ее интерполяции во всей области определения предлагается использовать функцию вида
неизвестна, для ее интерполяции во всей области определения предлагается использовать функцию вида  , где
, где 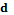 – мера близости между объектами. В качестве меры близости между объектами
– мера близости между объектами. В качестве меры близости между объектами  и
и 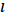 рассматривается взвешенное евклидово расстояние
рассматривается взвешенное евклидово расстояние ,
,  . (1)
. (1) подбираются с использованием метода Монте-Карло.
подбираются с использованием метода Монте-Карло. . (2)
. (2)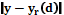 – разность между наблюдаемым и расчетным значениями выходного параметра;
– разность между наблюдаемым и расчетным значениями выходного параметра;  – объем исследуемой выборки.
– объем исследуемой выборки. для каждого прогнозируемого параметра. Значения коэффициентов
для каждого прогнозируемого параметра. Значения коэффициентов 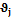 выбираются из интервала [0, 1], и для них должно выполняться условие нормировки
выбираются из интервала [0, 1], и для них должно выполняться условие нормировки  , где
, где 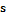 – количество прогнозируемых параметров.
– количество прогнозируемых параметров.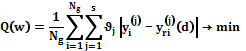 . (3)
. (3) задачу многомерной интерполяции функции
задачу многомерной интерполяции функции  в окрестностях каждого i-го узла многомерной сетки. Для этого относительно каждого i-го узла сетки пространства
в окрестностях каждого i-го узла многомерной сетки. Для этого относительно каждого i-го узла сетки пространства  . Далее, имея массив, состоящий из пар чисел
. Далее, имея массив, состоящий из пар чисел 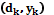
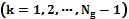 , решаем задачу экстраполяции дискретной зависимости
, решаем задачу экстраполяции дискретной зависимости  непрерывной функцией
непрерывной функцией  . При построении приближающей функции
. При построении приближающей функции  . В общем случае величина
. В общем случае величина  определяется в процессе предварительного вычислительного эксперимента. В качестве модели для приближения используется квадратичный полином
определяется в процессе предварительного вычислительного эксперимента. В качестве модели для приближения используется квадратичный полином 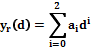 , в котором коэффициенты
, в котором коэффициенты 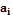 определяются из условия минимизации функционала
определяются из условия минимизации функционала  .
. , вычисляемого по формуле (2) или (3), продолжается до тех пор, пока число итераций, на протяжении которых не происходит улучшение решения, не превысит заранее заданное значение, либо пока расчетное значение средней абсолютной ошибки прогноза не упадет ниже априори заданной величины допустимой погрешности, либо пока не будет превышено максимальное время вычислений. Следует отметить, что особенностью эволюционного вычислительного процесса является то, что он может быть остановлен и продолжен в любой момент.
, вычисляемого по формуле (2) или (3), продолжается до тех пор, пока число итераций, на протяжении которых не происходит улучшение решения, не превысит заранее заданное значение, либо пока расчетное значение средней абсолютной ошибки прогноза не упадет ниже априори заданной величины допустимой погрешности, либо пока не будет превышено максимальное время вычислений. Следует отметить, что особенностью эволюционного вычислительного процесса является то, что он может быть остановлен и продолжен в любой момент.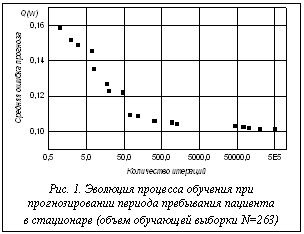 На рисунке 1 приведен график эволюции процесса обучения – изменение средней абсолютной ошибки прогноза в зависимости от количества итераций поиска решения. Зависимость получена при прогнозировании периода лечения в стационаре. Из рисунка 1 видно, что приемлемые результаты обучения достигаются уже при первых 500 итерациях, продолжение обучения до 500 000 итераций приводит к улучшению прогноза менее 1 %. Достоверность полученных результатов проверялась на контрольной выборке. На рисунке 2 показано распределение ошибки прогноза, полученное на контрольной выборке пациентов.
На рисунке 1 приведен график эволюции процесса обучения – изменение средней абсолютной ошибки прогноза в зависимости от количества итераций поиска решения. Зависимость получена при прогнозировании периода лечения в стационаре. Из рисунка 1 видно, что приемлемые результаты обучения достигаются уже при первых 500 итерациях, продолжение обучения до 500 000 итераций приводит к улучшению прогноза менее 1 %. Достоверность полученных результатов проверялась на контрольной выборке. На рисунке 2 показано распределение ошибки прогноза, полученное на контрольной выборке пациентов.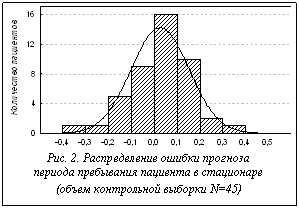 не снижая размерности признакового пространства, что, в свою очередь, позволяет исключить потерю значимой информации и учесть слабые связи в рассматриваемых информационных массивах.
не снижая размерности признакового пространства, что, в свою очередь, позволяет исключить потерю значимой информации и учесть слабые связи в рассматриваемых информационных массивах.