Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программа диагностики заболеваний
Аннотация:Диагностика базируется на расчете вероятностей болезней. Рассмотрено использование многомерных распределений, многократно определенных диагностических признаков, маркеров вирусных гепатитов и др. Созданная программа верно проводит дифференциальную диагностику механической и паренхиматозной желтух в 97 % случаев.
Abstract:There was developed a methodic of diagnostics based on computation of diseases probabilities. This methodic is using multivariate distribution, repeatedly defined symptoms, analyses and other data, markers of viral hepatitis, etc – are considered. There was written a program that makes differential diagnostics between obstructive and hepatocellular jaundice with effectiveness 97 %.
| Авторы: Жмудяк Л.М. (l_jmoudiak@hotmail.com) - Алтайский государственный технический университет им. И.И. Ползунова, г. Барнаул, доктор технических наук, Жмудяк А.Л. (l_jmoudiak@hotmail.com) - Алтайский государственный технический университет им. И.И. Ползунова, г. Барнаул, кандидат технических наук | |
| Ключевые слова: механическая желтуха, паренхиматозная желтуха, диагностические признаки, формула байеса, вероятность, диагностика, программа диагностики |
|
| Keywords: obstructive jaundice, hepatocellular jaundice, diagnostic signs, Bayes' formula, probability, diagnostics, diagnostics program |
|
| Количество просмотров: 17275 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
Разработанные методика и программа диагностики [1] были развиты и использованы для дифференциальной диагностики паренхиматозной и механической желтух. Тестирование на 564 историях болезней показало, что компьютерный диагноз верен в 97 % случаев. Паренхиматозная желтуха обусловлена вирусными (вирусные гепатиты A, B, C, D, G, TT и др.) и иными заболеваниями печеночной клетки, которые лечатся терапевтически. Механическая желтуха является следствием перекрытия (обтурации) желчных путей, например, камнями или опухолью, и зачастую требует срочного хирургического вмешательства. Эти совершенно разные по природе и тактике лечения заболевания имеют ряд схожих проявлений и затрудненную дифференциальную диагностику: процент диагностических ошибок колеблется от 8 до 30, что обусловливает практическую востребованность программы. Методика компьютерной диагностики базируется на расчете вероятностей болезней по формуле Байеса. Для диагностики использовались 36 дискретных и непрерывно распределенных диагностических признаков (ДП): регистрационно-биографические данные (пол, возраст и т.п.), данные анамнеза, симптомы заболевания, клинические анализы, данные инструментальных обследований пациента и др.
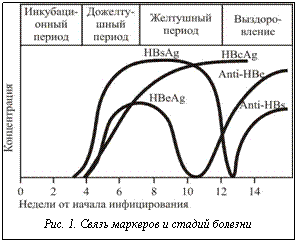
Всего рассматривается девятнадцать маркеров вирусных гепатитов. Необходимость анализа комбинаций маркеров обосновывается хотя бы следующим. Маркер HBsAg определяется не только в острой и хронической стадиях гепатита B, но и у практически здоровых людей – носителей этого антигена. По оценке вирусологов, в мире около 400 миллионов людей являются носителями HBsAg. (Информация о маркерах взята из работ [2–5]). По собранной и взятой из литературы статистике определены вероятности комбинаций положительных и отрицательных значений маркеров как при механической и паренхиматозной желтухах, так и при гепатитах А, В и С. Следование медицинским таблицам диагностических значений маркеров затрудняет описание всех возможных их сочетаний, поэтому проработана методика описания динамики маркеров. Приведем элементы этой методики для гепати- та В. Связь маркеров и стадий болезни отражена в методике с ориентировкой на приведенную на рисунке 1 схему. Сочетание положительных и отрицательных маркеров, определенных у больного, в программе сравнивается с динамикой маркеров. В зависимости от ситуации это является основанием для диагноза «острый вирусный гепатит B» или для расчета вероятности этого диагноза, а также для расчета вероятностей механической и паренхиматозной желтух. В известных работах при байесовской диагностике ДП считаются взаимонезависимыми, хотя понятно, что в едином организме ДП в общем случае зависят друг от друга. За время болезни и лечения ДП изменяются и определяются не один раз, хотя обычно при диагностике математическими методами используются ДП, определенные только один раз, в первый день болезни. ДП, определенные в другие дни, в расчетах не используются. То есть не учитывается динамика болезни – важнейший при постановке диагноза фактор. Однако авторам удалось учесть измерения одного и того же ДП в другие дни: повторные измерения одного и того же ДП были математически рассмотрены как новые отдельные ДП. То есть величина ДП, например, билирубина в 1-й день – это один ДП, билирубин во 2-й день – это математически другой ДП, билирубин в 5-й день – опять новый признак и т.д. Затем была найдена и учтена взаимозависимость между ДП, определенными в разные дни. Таким образом удалось учесть данные многократно определенных ДП, то есть динамику болезни. При создании описываемой методики была поставлена задача включения медицинских знаний в чисто математический подход. В качестве одного из решений этой задачи предложено использовать медицинские знания для уточнения и дополнения используемой статистики (собранной и используемой БД). Имеющиеся распределения ДП всегда получены (построены) по ограниченным выборкам. Медицинские знания позволяют эти распределения уточнить и дополнить. Таким уточнением и дополнением статистики в математический подход являются знания врача о физиологии и патофизиологии, течении болезни, воздействии лекарств и т.п. В подавляющем числе публикаций описывается расчет вероятностей болезней по одномерным распределениям. Переход к многомерным распределениям снял бы многие проблемы. Но сбор данных, достаточных для построения многомерных распределений, в большинстве случаев непосилен. Вместе с тем, используя доступную статистику, в ряде случаев можно по одномерным распределениям построить многомерные за счет медицинских знаний вследствие понимания взаимосвязи симптомов и анализов. Переход к многомерным распределениям важен, как минимум, для диагностики с расчетом вероятности болезни по формуле Байеса. Диагностические признаки заболевания взаимозависимы. Многомерное распределение органически содержит в себе взаимосвязь признаков заболевания, поэтому построение таких распределений избавляет от необходимости учета взаимозависимости признаков. Предельный случай – многомерное распределение всех признаков заболевания qj(a1, a2, a3, …, am), где j – номер болезни, ai (i=1, 2, 3, …, m) – признак заболевания. Если бы удалось построить такое распределение, отпала бы необходимость в расчете вероятности болезни по формуле Байеса. Действительно, определив у больного конкретные величины признаков ai: ai=a01, ai=a02 и т.п., сразу по зависимости qj(a1, a2, a3, …, am) получаем плотность вероятности qi. После этого сравниваются qi у распознаваемых болезней j=1, 2, 3, …, n и ставится диагноз; диагнозом считается болезнь, в распределении которой qi больше. Рассмотрим теперь практическую диагностику с расчетом вероятностей болезней по формуле Байеса. Результатом диагностики конкретного пациента являются вероятности каждой болезни. Сумма вероятностей болезней равна единице. По рассчитанным вероятностям ставится диагноз. Если болезней две и вероятность первой болезни (p1) не ниже вероятности второй болезни (p2), диагнозом может считаться первая болезнь. Рассмотрим случай, когда p1=51 %, p2=49 % (рис. 2, В). Здесь вероятности болезней практически неразличимы и делать однозначный вывод, по мнению авторов, нельзя. В другом случае, когда p1=94 %, p2=6 %, можно более уверенно говорить о диагнозе (рис. 2, А).
Созданная методика реализована в виде универсальной компьютерной программы, которая используется для диагностики механической и паренхиматозной желтух; точность диагностики – 97 % правильных, 1 % неправильных и 2 % неопределенных диагнозов. Программа написана на языке C++ Builder 6.0, имеет интуитивно понятный интерфейс, время диагностики одного пациента около 10 секунд. Программный продукт позволяет вести БД больных и заниматься научными исследованиями. Врач может смотреть динамику изменения ДП больного на фоне графика изменения ДП при обычном течении каждой из болезней, анализировать гистограммы ДП в разные дни заболевания, получать не только диагноз, но и влияние каждого ДП на него и т.п. Программа внедрена в трех больницах Алтайского края. Разработанная методика диагностики сравнивалась с лучшими методами диагностики: дискриминантный анализ, деревья классификации, нейронные сети. Напрямую сравнить методы не удалось. Чтобы воспользоваться известными программами, нужно для каждого больного иметь абсолютно все ДП, чего в реальной больнице не бывает. (Авторская программа работает с реальными ДП, определенными не в каждый день; она функционирует и тогда, когда определена только часть ДП.) В известные программы авторы ввели свои методические наработки, после чего эти программы в 90 % случаев стали показывать верный диагноз. Затем эти программы научили учитывать динамику заболеваний. Только после этого дискриминантный анализ и деревья классификации достигли точности диагностики 92 % и 93 %, а у нейронных сетей правильных диагнозов стало 96 % (у авторской методики – 97 %). То есть качественную диагностику нейронные сети показали только с использованием авторских наработок, включая учет динамики. Количество неверных диагнозов у нейронных сетей – 3 %, у авторской методи- ки – 1 %. В ходе сравнения было предположено, что нейросетевой (искусственных нейронных сетей) и вероятностный подходы могут быть взаимоусилены совмещением, состоящим в использовании в качестве исходных данных для искусственных нейронных сетей не исходных статистических данных, а их вероятностных характеристик. Литература 1. Жмудяк М.Л., Повалихин А.Н., Стребуков А.В., Гайнер А.В., Жмудяк А.Л., Устинов Г.Г. Диагностика заболеваний методами теории вероятностей. Барнаул: Изд-во АлтГТУ, 2006. 168 с. 2. Филиппова Н.Н., Комарова М.В. Вирусные гепатиты. URL: www.labdiagn.h1.ru/hepatit.shtml (дата обращения: 07.08.08). 3. Аммосов А.Д. Гепатит B. URL: http://www.vector-best.ru/brosh/gepb.htm (дата обращения: 05.08.08). 4. Хазанов А.И. Функциональная диагностика болезней печени. М.: Медицина, 1988. 304 с. 5. Harrison’s principles of Internal Medicine. 16th Edition. Editors: D.L. Kasper, E. Braunwald, A.S. Fauci, S.L. Hauser, D.L. Longo, J.L. Jameson. McGraw-Hill, Medical Publishing Division, New York, 2005, 2783 p. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2341 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Общие принципы системной оптимизации технологии контроля качества телерадиопродукции
- Интеллектуальная информационная система для решения задач прогнозирования неисправностей вагонного оборудования на железнодорожном транспорте
- Задача определения группы риска для однородных транспортных узлов
- Экспертная система мониторинга технологического процесса
- Подход к использованию меры возможности при оценке принимаемых решений
Назад, к списку статей



 На основании собранной БД были сформированы распределения ДП: отдельно по паренхиматозной желтухе и отдельно по механической. По распределениям определены выборочные плотности относительных частот (далее – плотности вероятностей) непрерывных ДП и выборочные относительные частоты (далее – вероятности) дискретных ДП. Эти плотности и вероятности подставляются в формулу Байеса. По вероятностям и плотностям вероятностей используемых ДП с помощью формулы Байеса вычисляются вероятности паренхиматозной желтухи и механической. При некоторых сочетаниях маркеров дополнительно вычисляются вероятности и диагностируются формы паренхиматозной желтухи, например, вероятность острого вирусного гепатита B.
На основании собранной БД были сформированы распределения ДП: отдельно по паренхиматозной желтухе и отдельно по механической. По распределениям определены выборочные плотности относительных частот (далее – плотности вероятностей) непрерывных ДП и выборочные относительные частоты (далее – вероятности) дискретных ДП. Эти плотности и вероятности подставляются в формулу Байеса. По вероятностям и плотностям вероятностей используемых ДП с помощью формулы Байеса вычисляются вероятности паренхиматозной желтухи и механической. При некоторых сочетаниях маркеров дополнительно вычисляются вероятности и диагностируются формы паренхиматозной желтухи, например, вероятность острого вирусного гепатита B. Если вероятность одной из болезней не только не ниже вероятностей других болезней, но и превышает установленный заранее уровень надежности диагноза, выбор делается в пользу этой болезни. Установим уровень надежности, равный 90 %. Для примера A получаем диагноз – болезнь 1, для примеров B и C диагноз неопределенный, то есть программа отказывается сделать выбор в пользу первой болезни и требует больше данных. Такой подход к оценке вероятностей позволяет перевести часть неправильно поставленных диагнозов в область неопределенных ответов. Одновременно некоторые правильные диагнозы также становятся неопределенными (как в примере С). Представляется, что важнее сделать меньше ошибок в диагнозе, чем большему числу пациентов поставить верный диагноз.
Если вероятность одной из болезней не только не ниже вероятностей других болезней, но и превышает установленный заранее уровень надежности диагноза, выбор делается в пользу этой болезни. Установим уровень надежности, равный 90 %. Для примера A получаем диагноз – болезнь 1, для примеров B и C диагноз неопределенный, то есть программа отказывается сделать выбор в пользу первой болезни и требует больше данных. Такой подход к оценке вероятностей позволяет перевести часть неправильно поставленных диагнозов в область неопределенных ответов. Одновременно некоторые правильные диагнозы также становятся неопределенными (как в примере С). Представляется, что важнее сделать меньше ошибок в диагнозе, чем большему числу пациентов поставить верный диагноз.