Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Методы анализа функциональных моделей
Аннотация:В статье предлагаются подходы к аналитическому исследованию структурно-функциональных моделей, построенных на основе методологии IDEF0.
Abstract:In this paper propose approach to analytics methods intending structure-functional models buildings on base of methodologies IDEF0
| Авторы: Ильин В.А. (komandor.99@mail.ru) - Санкт-Петербургский филиал НИИ «Центрпрограммсистем» (профессор, старший научный сотрудник НИЛ), г. Санкт-Петербург, Россия, доктор военных наук, Янча С.П. (iljin@interzet.ru) - Высшие специальные офицерские классы ВМФ, г. Санкт-Петербург | |
| Ключевые слова: марковский процесс, орграф, система, модель |
|
| Keywords: markov process, orgraf, system, mathematical model |
|
| Количество просмотров: 12989 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Метод структурного функционального моделирования материально-информационных систем имеет почти сорокалетнюю историю. Структурные функциональные модели используются в самых разных предметных областях – от бытовой сферы до военной (например, планирование в НАТО). Однако в нашей стране этот метод применяет только узкий круг специалистов, главным образом в области финансов, экономики и производства. Вместе с тем методология функционального моделирования (IDEF) официально определена рекомендациями по стандартам. Общая методология IDEF включает в себя ряд частных методологий. Одна из них, IDEF0, используется для создания функциональных моделей (ФМ), отображающих структуру и функции системы, а также потоки информации и материальных объектов, преобразуемые этими функциями. С помощью наглядного графического языка IDEF0 изучаемая система предстает перед разработчиками и аналитиками в виде набора взаимосвязанных функций (функциональных блоков – в терминах IDEF0). Целью создания любой системы является ее функционирование. Результат функционирования системы – осуществление ею материально-информационных обменов, то есть преобразований входов в выходы. Функционирование системы обеспечивается материальной инфраструктурой системы, составляющей ее устройство, ее морфологию. Характер (режим) функционирования системы в пределах морфологических возможностей определяется управлением работой системы. Именно особенности функционирования системы определяют и ее морфологию, и материально-информационные потоки. ФМ есть графическое представление функционирования систем и объектов. ФМ может использоваться как для анализа процессов, протекающих в существующих системах (их функционирование), так и для синтеза структур при проектировании новых систем. Однако анализ функциональных моделей в настоящее время на качественном уровне выполняется путем анализа структуры связей между отдельными функциями моделируемого процесса, сравнения различных структур процесса и различных процессов между собой. В незначительном количестве имеющихся источников и документов по методологии функционального моделирования не приводятся методы аналитического количественного анализа ФМ и процессов, ими описываемых. ФМ, представленную в нотации технологии IDEF0, можно рассматривать как орграф и, следовательно, анализировать с помощью матрицы смежностей (связей) функций процесса между собой. Кроме того, если моделируемый процесс является марковским, то к анализу ФМ применимы методы исследования марковских процессов.
Интерпретируя ФМ как орграф, сформируем матрицу связей функций моделируемого процесса (см. табл.). В матрице по строкам единицами и нулями записаны входы в функции, по столбцам, соответственно, выходы из функций. Суммы входов по строкам и выходов по столбцам позволяют ранжировать функции по степени важности в исследуемом процессе. Общая сумма входов и выходов позволяет сравнивать структуры одного процесса и разные процессы по их сложности. Матричная запись ФМ
Эффективность процесса может быть определена как среднее арифметическое четырех коэффициентов: В данном случае fΣ – общее количество функций исследуемого процесса; SΣ – общее число связей, то есть число единиц в матрице; Σin – сумма единиц в строке, то есть сумма входных связей функции процесса; В нашем примере Kм=0,51, Кс=0,621, Кр=0,483, Ки=0,913, Эп=0,627. Если функции, составляющие процесс, или хотя бы часть из них являются стохастическими, ФМ можно представить как марковский процесс с дискретными состояниями и дискретным временем, интерпретируемый неоднородной марковской цепью. Вероятность выполнения функции – условная вероятность этой функции от вероятностей предшествующих функций. Вероятность выполнения процесса в этом случае есть условная вероятность выполнения последней функции от вероятностей выполнения предшествующих функций. Для неоднородной марковской цепи связи между функциями будут мультипликативными. В этих условиях эффективность процесса можно определить как произведение вероятностей функций цепи от входа до выхода:
где рin – вероятность выполнения выходной функции; f – число функций в цепи от входа до выхода; pi – вероятность выполнения i-й функции в цепи процесса. Для представленного примера
Интерпретация ФМ в виде марковского процесса позволяет оптимизировать его методами математического программирования (динамическим или выпуклым программированием). Определенную сложность представляет оценка уровня подготовленности коллектива операторов больших систем или оператора, выполняющего сложную последовательность действий. Но если представить подготовку или деятельность как марковский процесс, заменив вероятности выполнения функций оценками операторов или оценками выполнения функций оператором от 0 до 1 и применив приведенный выше математический аппарат, можно сравнительно легко получить интегральную оценку подготовленности оператора или расчета. Более того, ФМ процесса подготовки позволяет выявить узкие места в системе подготовки, оптимизировать процесс подготовки методами математического программирования и принять соответствующие меры. Предлагаемые методы анализа общеизвестны. Однако при их применении к методу функционального моделирования исследователь получает наглядное представление процесса, сравнительно простой и достаточно эффективный аппарат анализа процессов любой сложности. Литература 1. Дубейковский В.И. Практика функционального моделирования с AllFusion Process Modeler. М.: Диалог-МИФИ, 2004. 364 с. 2. Харари Ф. Теория графов. М.: Книжный дом «ЛИБРОКОМ», 2009. 296 с. 4. Баруча-Рид А.Т. Элементы теории марковских процессов и их приложения. М.: Наука, 1969. 504 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2364 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Некоторые технологические аспекты создания учебно-тренировочных средств подготовки командиров и специалистов Военно-морского флота
- Метод оценки вероятности принятия ошибочных решений при дискриминационном анализе транспортных узлов
- Архитектура системы информационно-имитационного моделирования поддержки жизненного цикла ИТ-инфраструктуры
- Информационное обеспечение процессов развития больших систем административно-организационного управления
- Прогнозирование временного ряда инфекционной заболеваемости
Назад, к списку статей



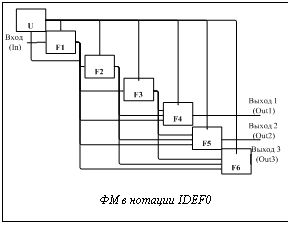 Для примера рассмотрим некий абстрактный процесс, представленный в нотации технологии IDEF0 (см. рис.). Процесс включает в себя 6 процедурных функций (F1, …, F6), выполняющих обработку информации, и одну специфическую функцию управления процессом (U), связанных между собой прямыми и обратными функциональными связями. Процесс имеет один вход из внешней среды (может быть, из другого процесса, In) и три выхода во внешнюю среду (во внешние процессы, Out1, …, Out 3). Как видно, вход из внешней среды осуществляется через функцию F1, обеспечивающую обработку входной информации и ее передачу другим функциям. Выход осуществляется функциями F4, F5, F6, которые, очевидно, решают основные задачи процесса, остальные функции решают обеспечивающие задачи. Следует заметить, что количество входов и выходов в общем случае может быть любым и определяется только структурой исследуемого процесса.
Для примера рассмотрим некий абстрактный процесс, представленный в нотации технологии IDEF0 (см. рис.). Процесс включает в себя 6 процедурных функций (F1, …, F6), выполняющих обработку информации, и одну специфическую функцию управления процессом (U), связанных между собой прямыми и обратными функциональными связями. Процесс имеет один вход из внешней среды (может быть, из другого процесса, In) и три выхода во внешнюю среду (во внешние процессы, Out1, …, Out 3). Как видно, вход из внешней среды осуществляется через функцию F1, обеспечивающую обработку входной информации и ее передачу другим функциям. Выход осуществляется функциями F4, F5, F6, которые, очевидно, решают основные задачи процесса, остальные функции решают обеспечивающие задачи. Следует заметить, что количество входов и выходов в общем случае может быть любым и определяется только структурой исследуемого процесса.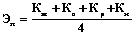 , где Км – масштабный коэффициент процесса,
, где Км – масштабный коэффициент процесса,  , оценивает количество функций в процессе (чем больше масштабный коэффициент, тем сложнее процесс); Кс – коэффициент связанности функций процесса,
, оценивает количество функций в процессе (чем больше масштабный коэффициент, тем сложнее процесс); Кс – коэффициент связанности функций процесса,  , оценивает коммуникативность функций в процессе (более сложный процесс имеет больший коэффициент связанности); Кр – коэффициент равномерности распределения функций в процессе,
, оценивает коммуникативность функций в процессе (более сложный процесс имеет больший коэффициент связанности); Кр – коэффициент равномерности распределения функций в процессе,  (чем меньше коэффициент равномерности, тем лучше структурирован процесс); Ки – коэффициент изолированности функций, определяет общее число несвязанных функций,
(чем меньше коэффициент равномерности, тем лучше структурирован процесс); Ки – коэффициент изолированности функций, определяет общее число несвязанных функций,  , то есть функций, не имеющих входов или выходов. Изолированные функции не влияют на качество процесса.
, то есть функций, не имеющих входов или выходов. Изолированные функции не влияют на качество процесса.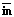 – среднее число входных связей; Σout – сумма единиц в столбце, то есть сумма выходных связей функции процесса;
– среднее число входных связей; Σout – сумма единиц в столбце, то есть сумма выходных связей функции процесса; 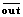 – сумма единиц в столбце, то есть среднее число выходных связей; пстр – число пустых строк (число функций без входов); псто – число пустых столбцов (функций без выходов).
– сумма единиц в столбце, то есть среднее число выходных связей; пстр – число пустых строк (число функций без входов); псто – число пустых столбцов (функций без выходов). ,
,
