Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Формальный метод транскрипции иностранных имен собственных на русский язык
Аннотация:Статья посвящена созданию математического формализма, описывающего процесс транскрипции имен собственных с иностранного языка на русский. Формализм позволяет перейти к программной реализации подобных систем.
Abstract:The paper devoted to the mathematical formalism creation describing process of proper names transcription from different foreign languages into Russian. The formalism allows to solve the task of program such systems realization.
| Авторы: Бондаренко А.В. (bond@fgosniias.ru) - Московский физико-технический институт (государственный университет) (профессор ), Долгопрудный, Россия, доктор физико-математических наук, Визильтер Ю.В. (viz@GosNIIAS.ru) - Государственный научно-исследовательский институт авиационных систем, г. Москва, кандидат технических наук, Горемычкин В.И. (gwi@fgosniias.ru) - Государственный научно-исследовательский институт авиационных систем, г. Москва, Клышинский Э.С. (klyshinsky@itas.miem.edu.ru) - Московский государственный институт электроники и математики (технический университет), кандидат технических наук | |
| Ключевые слова: фонетические параметры, формальная модель, машинная транскрипция |
|
| Keywords: phonetic parameters, formal model, machine transcription |
|
| Количество просмотров: 14272 |
Версия для печати Выпуск в формате PDF (4.03Мб) Скачать обложку в формате PDF (1.25Мб) |
На практике часто встает вопрос о корректной передаче имен собственных с одного языка на другой. При этом одним из основных требований является адекватная передача их звучания. Известно несколько методов передачи имен. Наиболее распространенным является транслитерация, при которой символу или набору символов одного алфавита ставится в соответствие один или несколько символов другого алфавита, причем соответствие проводится, скорее, по их графическому сходству. Данный метод записи позволяет восстановить исходное написание слова, однако не дает возможности воспроизвести его звучание лицу, не знакомому с исходным языком. Более удобным является словарный метод, при котором соответствие слов входного языка словам выходного языка задается при помощи некоторого фиксированного словаря. Однако количество имен собственных с каждым годом растет, в связи с этим построить всеобъемлющий словарь на практике чрезвычайно сложно. Возможен вариант наращивания объемов словаря, но он требует привлечения специалистов, знакомых с языком, на постоянной основе. Наиболее удобным является метод транскрипции, в котором звучание слова в одном языке записывается средствами другого языка (в том числе специализированного). Например, при фонетической транскрипции в качестве выходного может использоваться язык записи фонетики, позволяющий отразить все нюансы произношения слова. Однако подобный язык знаком лишь узкому кругу специалистов, в связи с чем, как правило, используют метод практической транскрипции, в котором звучание слова записывается алфавитом некоторого существующего языка. С практической транскрипцией связаны следующие основные проблемы. · Неполное соответствие фонемного состава двух языков. Так, например, в русском языке отсутствуют арабские горловые звуки, в связи с чем различные (с точки зрения араба) имена будут переданы на русский язык одинаковым образом. · Вынужденное использование запрещенных в целевом языке морфем. Так, например, в русском языке появляются такие слова, как «парашют», использующие сочетание «шипящая согласная + ю или я». · Зачастую транскрипция делается не с исходного языка, а с его транслитерации при помощи латиницы. Это распространяется на китайский, арабский, другие языки, использующие иные графические системы (иероглифы или вязь). В таком случае при транслитерации теряется часть информации, а транскрипция усугубляет проблему. · Историческая традиция. Традиционно Hamlet передается как Гамлет, хотя по современным правилам такое имя должно писаться как Хэмлет или Хемлет. Не помогает и фиксация записи в словаре. Так, имя Walpol в разное время записывалось в словарях как Вальполь, Вальпол и, наконец, Уолпол. · Отсутствие единых устоявшихся правил передачи. Как уже упоминалось, одно и то же имя может быть корректно передано по-разному. Результат зависит от того, какого набора правил передачи из многих существующих мы придерживаемся. Один и тот же учебник может рекомендовать несколько вариантов. Заметим также, что в ряде случаев в самом исходном языке имя может читаться не в соответствии с правилом, а по сложившейся традиции. Яркий пример – английский язык, в котором многие фамилии читаются по традиции, привнесенной нормандскими завоевателями или шотландскими подданными. Для решения подобной проблемы можно использовать в качестве вспомогательного словарный метод, когда слово сначала ищется в словаре, а при отсутствии соответствия – транскрибируется по правилам. В данной предметной области отечественная лингвистика подготовила хорошую теоретическую базу, основанную на классических работах по практической транскрипции [1–3], в которых дается подробное описание правил транскрипции для большого количества языков. Современный уровень информатизации требует создания ПО, осуществляющего автоматическую транскрипцию. Для этого необходимо предварительно создать адекватную математическую модель. В зарубежных публикациях на эту тему наиболее распространены подходы, основанные на скрытых марковских моделях [4] и конечных автоматах [5]. Однако первый подход использует вероятностную передачу имен, что не всегда гарантирует корректность. При втором подходе учет контекста передачи организован слишком сложно, что затрудняет внесение изменений в правила транскрипции. В связи с этим авторами был разработан новый метод, основанный на декларативном подходе, отделяющем правила транскрипции от формального аппарата. Транскрипция с использованием формально-литеральной записи Определим алфавит A={a1,a2,a3,…as}, |A|=s, s>1 как любое конечное множество символов. Словом Параметр литеры определим как пару Параметр литеры указывает некоторые характеристики, важные для транскрипции или позволяющие классифицировать символы алфавита по группам. Например: <²ряд², ²передний²>,<²тип², ²гласная²>, <²ударение², ²безударная²>. Заметим, что имя и значение параметра литеры также являются словами, однако их символы могут принадлежать алфавиту, удобному для формирования правил транскрипции. Под литерой здесь понимается некоторое упорядоченное множество, описывающее не только символ, но и множество параметров, приписываемых данному символу по умолчанию при его озвучивании. Будем считать, что литера состоит из символа, однозначно идентифицирующего ее, и набора параметров, либо изначально присущих данной литере, либо отражающих ее положение в слове. Введем три алфавита: AIN – входной алфавит, содержащий символы входного языка; AOUT – выходной алфавит, содержащий символы выходного языка и служебный символ #; ALIT – литеральный алфавит, используемый для идентификации литер. Алфавиты могут быть определены на пересекающихся или непересекающихся множествах символов. В случае передачи иностранных имен средствами русского языка входной алфавит состоит из символов стандартной латиницы, выходной алфавит – из кириллических символов, принятых в русском языке, а литеральный алфавит – из символов входного и выходного алфавитов, а также служебных символов: BEG, END (символы начала и конца слова соответственно), Æ (пустой символ). Теперь литера может быть формально определена как пара Формальной литеральной записью (ФЛЗ) слова При этом считаем, что различные написания одного и того же символа из AIN (например, строчное и прописное или начальное, срединное, конечное и изолированное) идентифицируются одним и тем же символом из ALIT, однако могут обладать (в зависимости от особенностей применения) различными значениями определенных параметров. Набор используемых параметров определяется значимостью различения тех или иных написаний при транскрипции и особенностями языка. Пример литеры: <¢A¢,{< ²тип², ²гласн²>, <²написание², ²прописн²>, <²ряд², ²задний²>}>, где ¢А¢ – литеральный символ, идентифицирующий символ входного алфавита, а множество, заключенное в фигурные скобки, – множество параметров данной литеры. Служебные символы, пред- назначенные для обеспечения процесса транскрипции, будут далее обозначаться несколькими символами и не будут заключаться в апострофы. Определим также операторы сравнения литер. Оператор равенства = производит сравнение как литеральных символов, так и наборов параметров литер, то есть литеры Оператор условного равенства » производит сравнение только наборов параметров литер и применяется лишь в том случае, если в одной из литер литеральный символ принимает значение Æ. Литеры Собственно процесс транскрипции осуществляется в три этапа: 1) преобразование написания слова на входном языке в формальную литеральную запись; 2) выделение слогов, расстановка переносов и ударений; 3) перевод ФЛЗ слова в запись на кириллице. Рассмотрим каждый из них подробнее. Преобразование написания слова на входном языке в ФЛЗ Для преобразования слова Примеры правил преобразования в ФЛЗ: ¢A¢®<’A’,{<²тип², ²гласн²>, <²написание², ²прописн²>, <²ряд²,²задн²>}>> ¢a¢®<’A’,{<²тип², ²гласн²>, <²написание², ²строчн²>, <²ряд²,²задн²>}>> ¢B¢®<’B’,{<²тип², ²согласн²>, <²написание², ²прописн²>, <²звонкость²,²звонкая²>}>> ¢b¢®<’B’,{<²тип², ²согласн²>, <²написание²,²строчн²>, <²звонкость²,²звонкая²>}>> (Курсивом выделена часть правила, относящаяся к литере.) На данном этапе для всех символов входного слова последовательно находятся такие правила, что символ, входящий во входное слово Пусть i=1,...,n, j=1,...,m, где n – общее количество литер в выходном слове; m – общее количество символов во входном слове; j не убывает при увеличении n. Тогда 1) 2) 3) 4) 5) 6) Выделение слогов и расстановка ударений На данном этапе определяются закрытые/открытые слоги и ударные/безударные буквы. Любая литера, находящаяся в конце слога, приобретает дополнительный параметр «литера в слоге» со значением «открытая». Для остальных литер значение этого параметра – «закрытая». Выделение слогов производится по следующему алгоритму. Для алфавита каждого языка может быть задан набор слогообразующих символов входного алфавита. В качестве части слога, присоединяемой к слогообразующему символу, берется половина символов между двумя слогообразующими. При нечетном количестве символов средний передается следующему слогу. Исключение делается для приставок, суффиксов и окончаний, в которых разделение на слоги фиксировано. Они присоединяются к остальной части слова как отдельный слог или несколько выделенных фиксированным образом слогов. Написание и деление на слоги таких приставок, суффиксов и окончаний задается отдельной базой правил. Следует отметить, что известны различные алгоритмы выделения слогов с точки зрения фонетики. Описанный алгоритм был выбран для упрощения практической реализации. Расстановка ударений и выделение слогов не являются обязательными процедурами. Их необходимо производить лишь для тех языков, в которых буквы читаются по-разному в зависимости от того, в какой позиции находится данная буква – в ударной, безударной или в конце слога. При расстановке ударений в языках, где ударение является критичным, фиксируются номер слога и направление, в котором ведется счет слогов, – от начала или от конца слова. Однако если в слове меньше слогов, чем указано в правиле расстановки ударений, ударение будет ставиться на последний слог при счете слогов с начала или на первый при счете с конца. Преобразование ФЛЗ слова в кириллицу На данном этапе на основе последовательности литер формируется кириллическое представление, отражающее фонетический облик слова. Подстрокой ФЛЗ назовем подмножество последовательно идущих литер данной ФЛЗ. Обозначим через Под правилом перевода будем понимать Rt: Будем считать, что перевод подстроки Пусть имеются некоторая ФЛЗ 1) 2) 3) 4) i1=1; 5) ik+1=ik+lk для kÎ(1,n) и in+ln=q+1; 6) " k,m $ RtÎÂ: где Результатом транскрипции является конкатенация результатов последовательного применения правил перевода Перейдем к непосредственному описанию алгоритма преобразования ФЛЗ слова в кириллицу. Поскольку данный алгоритм носит рекурсивный характер, описание удобно вести в терминах рекурсивно вызываемых функций. Определим функцию findRules( Шаг 1. Для каждого правила во множестве Ât выполняется следующее. Шаг 1.1. Каждое очередное правило рассматривается в качестве кандидата на применение к ФЛЗ Шаг 1.2. Начиная с полученной текущей позиции, последовательно проверяем сравнимость литер строки с литерами правила. Если хотя бы одна литера строки не сравнима с соответствующей литерой правила, считаем, что правило неприменимо, и переходим к следующему правилу (шаг 1.1). Если сравнение всех литер прошло успешно, данное правило добавляется во множество Шаг 2. На множестве Определим также рекурсивную функцию transcript( Шаг 1. Если последнее значение в списке Шаг 2. Текущая позиция i устанавливается равной последнему значению, помещенному во множество Шаг 3. Проверяются следующие условия. Шаг 3.1. Если множество Шаг 3.2. Для всех элементов Выходом алгоритма является множество С учетом введенных функций соответствующий алгоритм преобразования ФЛЗ слова в кириллицу имеет следующий вид. Пусть входом алгоритма является ФЛЗ слова Шаг 1. Обнулить списки Шаг 2. Вызвать функцию transcript( Результатом работы алгоритма будет множество Пример транскрипции с французского языка именной группы «Mireille Mathieu». Пусть преобразование в ФЛЗ осуществлено и каждому символу сопоставлена литера. Тогда процесс применения правил перевода будет иметь следующий вид (здесь последовательность строк таблицы соответствует последовательности применения правил).
Заметим, что в правилах (E на конце слова = '') и (согласная + IEU=ЬЕ) играют роль параметры, приписанные литерам, а также специальные символы. На основе предложенного метода была разработана программная технология транскрипции имен собственных. Тестирование показало, что реализованная на базе этой технологии система перевода допускает менее 1 % ошибок для таких языков, как немецкий, румынский и японский. Для английского языка количество ошибок приближается к 2 %, но может сокращаться за счет расширения словаря исключений. В настоящей работе обсуждались вопро- сы создания метода машинной транскрипции имен собственных с иностранного языка на русский. Основной упор сделан на передачу фонетического облика имени собственного с использованием возможностей русских фонетики и орфографии. Предложенный метод позволяет в удобной форме создавать правила для машинной транскрипции. Кроме того, он позволяет перейти к решению задачи автоматического порождения правил по имеющейся прецедентной базе, то есть по корпусу имен, транскрибированных экспертом. Это может стать предметом дальнейших исследований. Литература 1. Суперанская А.В. Теоретические основы практической транскрипции. М.: Наука, 1978. 283 с. 2. Гиляревский Р.С., Старостин Б.А. Иностранные имена и названия в русском тексте: справочник, 3-е изд. М.: Высш. шк., 1985. 304 с. 3. Зиндер Л.Р. Общая фонетика. М.: Высш. шк., 1979. 309 с. 4. Rabiner L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition // Proceedings of the IEEE. 1989. № 77, pp. 257–286. 5. Knight K., Graehl J. Machine Transliteration // In Proceedings of ACL Workshop on Computational Approaches to Semitic Languages, Philadelphia, USA, 1997. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2461 |
Версия для печати Выпуск в формате PDF (4.03Мб) Скачать обложку в формате PDF (1.25Мб) |
| Статья опубликована в выпуске журнала № 1 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



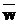 в алфавите A длины n назовем конечную последовательность символов алфавита A;
в алфавите A длины n назовем конечную последовательность символов алфавита A; 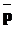 =<
=<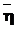 ,
, 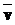 >, где
>, где  =
= >, где c – фиксированный символ из ALIT, идентифицирующий данную литеру, а
>, где c – фиксированный символ из ALIT, идентифицирующий данную литеру, а  =<
=<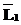 и
и 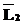 равны (
равны (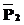 Í
Í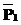 .
.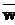 , совпадает с символом из найденного правила. ФЛЗ
, совпадает с символом из найденного правила. ФЛЗ 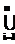
 , причем
, причем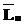 :=,
:=,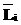 :=
:=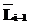 получено по правилу 4, а
получено по правилу 4, а 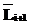 получено по правилу 3,
получено по правилу 3,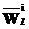 подстроку ФЛЗ
подстроку ФЛЗ 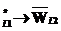 , где
, где  – литеральная подстрока-образец;
– литеральная подстрока-образец; 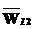 – подстрока-результат, состоящая из символов выходного алфавита. Правило Rt:
– подстрока-результат, состоящая из символов выходного алфавита. Правило Rt:  , если подстрока-образец
, если подстрока-образец 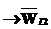 , применимое к
, применимое к 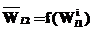 , преобразующей ФЛЗ в выходную строку. С учетом введенных определений и обозначений решение задачи перевода ФЛЗ в кириллическое представление может быть описано следующим образом.
, преобразующей ФЛЗ в выходную строку. С учетом введенных определений и обозначений решение задачи перевода ФЛЗ в кириллическое представление может быть описано следующим образом.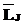 > и набор правил перевода Ât. Тогда перевод ФЛЗ в кириллическое представление будет заключаться в нахождении и применении упорядоченного подмножества правил Â=
> и набор правил перевода Ât. Тогда перевод ФЛЗ в кириллическое представление будет заключаться в нахождении и применении упорядоченного подмножества правил Â=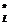 ®
®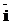 =, где n – число правил в подмножестве Â;
=, где n – число правил в подмножестве Â;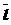 =;
=; q – общая длина выходного слова;
q – общая длина выходного слова;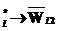 ,
,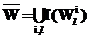 .
.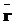 ), извлекающую из множества Ât подмножество правил
), извлекающую из множества Ât подмножество правил  ), преобразующую ФЛЗ в кириллическое написание и получающую в качестве входных параметров, передаваемых по значению, исходную ФЛЗ
), преобразующую ФЛЗ в кириллическое написание и получающую в качестве входных параметров, передаваемых по значению, исходную ФЛЗ 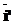 =
= , список
, список 