Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Фрактальная модель лесных пожаров
Аннотация:В работе построена модель лесного пожара, учитывающая фрактальный характер фронта горения. Найдены ана-литические зависимости скорости распространения лесного пожара и размеров сгоревшего участка от фрактальной размерности, времени и параметров лесного массива. Составлена и реализована программа по вычислению фрак-тальной размерности лесных массивов по данным аэрофотосъемки.
Abstract:In this work the model of forest fire considering fractal character of front of burning is constructed. Analytical associations of a velocity of distribution of forest fire and sizes of the burnt down site on fractal dimension, time and large forest parameters are discovered. The program on computation of fractal dimensions of forested area by data of aerial photo coverage is made and realized.
| Авторы: Кудинов А.Н. (tsvet@tversu.ru) - Тверской государственный университет, доктор физико-математических наук, Цветков В.П. (tsvet@tversu.ru) - Тверской государственный университет, Цветков И.В. (tsvet@tversu.ru) - Тверской государственный университет, доктор физико-математических наук | |
| Ключевые слова: фрактальный анализ, фронт горения, лесной пожар, математическая модель |
|
| Keywords: fractal analysis, front of burning, forest fire, mathematical model |
|
| Количество просмотров: 12617 |
Версия для печати Выпуск в формате PDF (4.97Мб) Скачать обложку в формате PDF (1.38Мб) |
Леса занимают более 74 % территории РФ, и каждый лесной пожар наносит существенный вред экономике. Так, по данным МЧС РФ, в 2008 г. произошло более 30 тысяч лесных пожаров, а общая площадь лесных массивов, охваченных огнем, составила более 1 млн га [1]. Наиболее часто возникают низовые лесные пожары, при которых выгорают лесная подстилка, подрост и подлесок, травянистый и кустарниковый покров, валежник, корневища деревьев и т.п. В засушливый период при ветре могут возникать верховые пожары, при которых огонь распространяется по кронам деревьев преимущественно хвойных пород. Горение торфа может вызвать подземные пожары. В последние годы наука существенно продвинулась в разработке математических моделей лесных пожаров [2]. Целью настоящей работы является построение модели лесных пожаров, учитывающей фрактальные свойства этих явлений. Фрактальные свойства лесных пожаров очевидны из тесной аналогии фронта горения и береговой линии. Фрактальный характер свойства береговой линии рассмотрен подробно в [3]. Одна из главных характеристик лесного пожара – скорость его распространения V. Для низового пожара характерная скорость VH составляет 0,1–3 м/мин., для верховых лесных пожаров температура в очаге достигает 1100 оС, а скорость их распространения VB при ветре – 100 м/мин. При безветрии скорость распространения лесного пожара ниже, VB»2–3 км/час. Нормальная скорость пламени лесного пожара, если фронт горения представляет гладкую кривую, может быть оценена как Фрактальный характер кривой фронта горения эффективно будет увеличивать значение d по сравнению с гладким фронтом. Длина фрактальной кривой L существенно зависит от масштаба [3]: Фрактальный характер зоны горения эффективно увеличивает ширину зоны горения, а именно В результате скорость распространения лесного пожара v с учетом фрактальности фронта горения имеет вид
Значение D можно оценить по измерению фрактальной размерности участка леса до возгорания по данным аэрофотосъемки. Как фрактальная размерность фронта горения, так и фрактальная размерность изображения участка леса на снимке определяются геометрией расположения его деревьев и кустов, поэтому вполне разумно считать их значения достаточно близкими.
Далее производился отсев отдельных элементов, размером меньше заданного, не имеющих связи между собой. После чего задавались начальное и конечное значения шага сетки и число промежуточных замеров. Фрактальная размерность определялась как тангенс угла наклона прямой, аппроксимирующей зависимость числа ячеек сетки, в которые попали элементы изображения, от шага сетки в дважды логарифмических координатах. Для компенсации ошибки метода производилось нормирование полученного результата по изображению, сгенерированному специальной программой создания изображения из случайно окрашенных элементов, близких по характерному размеру элементам анализируемого изображения. Были проанализированы снимки, выполненные с самолета локатором бокового обзора, ряда участков леса в Осташковском районе Тверской области. В ходе исследований получены значения в диапазоне D=1,44–1,53. Из (1) следует, что на первых этапах возгорания h»hmin, то есть скорость распространения огня минимальна. Само значение v0 будет определяться конечным состоянием леса в зоне возгорания, погодными условиями, состоянием и структурой подлеска, леса и характером ветра. При h>>hmin величина v будет существенно больше v0. Так, при h=1 км и hmin=10 м и D=1,5 имеем v=10v0, то есть скорость v возрастает на порядок. На основе формулы (1) получена интересная закономерность
где Сравнение (2) с опытными данными позволяет сделать оценку D непосредственно по наблюдению за зависимостью скорости лесного пожара от его размеров. График зависимости логарифма отношения На основании (1) составлено дифференциальное уравнение, определяющее зависимость диаметра области пожара от времени. Используя соотношение h=v и (1), получим
Обезразмерим (5), введя переменную Тогда из (3) следует
где H=2–D – постоянная Херста. Рассмотрим несколько характерных значений H и D при H=1 и D=1: H=hminv0t. (5) Формула (5) соответствует гладкому фронту горения и описывает линейный характер роста размера области горения лесного массива. При H=0,5 и D=1,5
В данном случае получен параболический нелинейный рост h с ростом времени. Очевидно, что тушение такого лесного пожара надо проводить в кратчайшее время. И наконец, если H=0 и D=2, то
Этот случай, на взгляд авторов, описывает наиболее быстрый, почти мгновенный характер горения лесного массива. Из построенной математической модели лесного пожара, учитывающей фрактальный характер фронта горения, следуют два важных вывода. Скорость распространения лесного пожара v можно существенно уменьшить, увеличивая hmin и уменьшая D. А этого можно достичь, проводя санитарную рубку деревьев и кустов и соблюдая геометрический порядок при высадке лесонасаждений. Литература 1. URL: www.mchs.gov.ru (дата обращения: 06.06.2009). 2. Эндрюс П., Финни М. Новый взгляд на лесные пожары // В мире науки. 2007. № 10. 3. Мандельброт Б. Фрактальная геометрия природы. М.: Наука, 1992. 4. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988. Т. 6. 5. Тищенко А.П., Цветков И.В. Фрактальная размерность текстур природных объектов и их идентификация методом фрактального анализа // Моделирование сложных систем: тематич. сб. Тверь: Изд-во ТвГУ, 1998. Вып. 1. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2538 |
Версия для печати Выпуск в формате PDF (4.97Мб) Скачать обложку в формате PDF (1.38Мб) |
| Статья опубликована в выпуске журнала № 2 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Концепция математического и компьютерного моделирования тепловых процессов в электронных системах
- Модели планирования производства изделий, основанных на нанотехнологиях
- Комплекс программных средств для исследования погрешности измерений экспериментального лазерного кругломера
- Программная реализация математической модели вариативности сердечного ритма
- Моделирование программы таксономии технологий изготовления деталей машиностроительного профиля с помощью сетей Петри
Назад, к списку статей



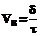 . Здесь t – характерное время горения; d – ширина зоны горения [4].
. Здесь t – характерное время горения; d – ширина зоны горения [4]. . Здесь D – значение фрактальной размерности; L0 – значение L для гладкой кривой D=1. В нашем случае
. Здесь D – значение фрактальной размерности; L0 – значение L для гладкой кривой D=1. В нашем случае  , где h – размер зоны горения; hmin – минимальное расстояние между фрагментами в зоне горения. Величина h имеет порядок размера участка выгоревшего леса, hmin – порядок характерного расстояния между деревьями и кустарниками горящего леса.
, где h – размер зоны горения; hmin – минимальное расстояние между фрагментами в зоне горения. Величина h имеет порядок размера участка выгоревшего леса, hmin – порядок характерного расстояния между деревьями и кустарниками горящего леса. , где d0 – ширина зоны горения для гладкого фронта.
, где d0 – ширина зоны горения для гладкого фронта. . (1)
. (1)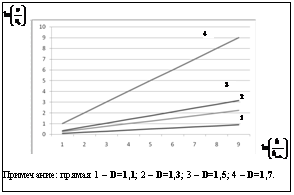 В работе [5] был описан один из способов определения фрактальной размерности изображений. На основе классического клеточного алгоритма, предложенного в [3], в среде программирования Delphi была создана программа определения фрактальной размерности изображения в формате *.bmp. На вход программы подавались изображения, отсканированные в 256 оттенках серого с разрешением не менее 1000 точек/дюйм. Для каждого изображения по тестовому участку выбирался пороговый уровень серого, на основе которого изображение переводилось в двутоновое.
В работе [5] был описан один из способов определения фрактальной размерности изображений. На основе классического клеточного алгоритма, предложенного в [3], в среде программирования Delphi была создана программа определения фрактальной размерности изображения в формате *.bmp. На вход программы подавались изображения, отсканированные в 256 оттенках серого с разрешением не менее 1000 точек/дюйм. Для каждого изображения по тестовому участку выбирался пороговый уровень серого, на основе которого изображение переводилось в двутоновое. , (2)
, (2) ,
,  .
. от логарифма отношения
от логарифма отношения  при различных значениях D приводится на рисунке в дважды логарифмических координатах.
при различных значениях D приводится на рисунке в дважды логарифмических координатах. . (3)
. (3) , и будем считать h(t=0)=hmin, то есть y(t=0)=1.
, и будем считать h(t=0)=hmin, то есть y(t=0)=1.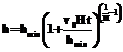 , (4)
, (4) . (6)
. (6)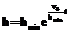 . (7)
. (7)