Вейвлет-преобразования используются для решения широкого класса задач, в которых анализируется нестационарный сигнал. Наиболее известны задачи, связанные со сжатием информации, подавлением шумов, обработкой и синтезом сигналов, анализом изображений, обработкой электрокардиограмм, анализом сейсмологических данных.
Для решения задач, в основе которых лежат вейвлет-преобразования, необходима быстрая компьютерная реализация алгоритма разложения и восстановления сигнала. Эффективная реализация алгоритма позволит применять вейвлет-преобразования в программах, работающих в режиме реального времени, например, для вейвлет-преобразования голосового трафика, идущего от VoIP-клиента.
Пусть имеется сигнал S(t).
Определение. Вейвлет – это функция 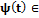
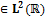 с нулевым средним значением
с нулевым средним значением
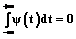 . (1)
. (1)
В результате масштабирования 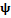 на величину m и сдвига на k получаем семейство таких функций (см. [1]):
на величину m и сдвига на k получаем семейство таких функций (см. [1]):
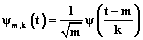 . (2)
. (2)
Пространство 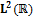 можно описать через иерархические вложенные подпространства VmÌ
можно описать через иерархические вложенные подпространства VmÌ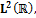 m=0, ±1, ±2, …, которые не пересекаются, а их объединение в пределе дает
m=0, ±1, ±2, …, которые не пересекаются, а их объединение в пределе дает 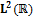 . Для пространства V0 существует функция j(t)ÎV0, называемая масштабирующей, ее целочисленные сдвиги по аргументу образуют ортонормированный базис пространства V0:
. Для пространства V0 существует функция j(t)ÎV0, называемая масштабирующей, ее целочисленные сдвиги по аргументу образуют ортонормированный базис пространства V0:
j0,k=j(t-k), k=0, ±1, ±2, ... (3)
При разложении функции на вейвлетные ряды для заданного уровня m используют функцию
s(t)=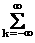 Cm,kjk(t)+
Cm,kjk(t)+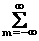
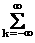 Dm,k ymk(t), (4)
Dm,k ymk(t), (4)
где Cm,k, Dm,k – аппроксимирующие и детализирующие коэффициенты вейвлет-преобразования.
Значения коэффициентов вычисляются следующим образом [2]:
Cm,k=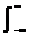 s(t)jmk(t) dt, (5)
s(t)jmk(t) dt, (5)
Dm,k= s(t)ymk(t)dt . (6)
s(t)ymk(t)dt . (6)
Большинство используемых вейвлетов не имеют аналитического представления, и для практических расчетов достаточно знать не сами вейвлеты, а их коэффициенты hi. Набор коэффици- ентов hi будет однозначно определять масшта- бирующую функцию ϕ(t) и материнский ψ(t) вейвлет:
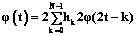 , (7)
, (7)
 (8)
(8)
 , (9)
, (9)
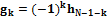 , (10)
, (10)
где N – число коэффициентов фильтра.
Одним из самых используемых типов вейвлетов являются вейвлеты Добеши. Добеши первой построила семейство ортогональных вейвлетов, которым соответствуют конечные фильтры hk, таким образом, что все значения коэффициентов фильтра не были очень малы. Для ортогональных вейвлетов существует быстрый алгоритм разложения – алгоритм Малла.
Входом для алгоритма данных служит сигнал, что на практике означает использование массива данных исходных значений определенной дли- ны N. По исходному сигналу строятся два сигнала длины N/2. Первый из них, аппроксимирующий, получается обработкой исходного сигнала фильтром коэффициентов hk масштабирующей функции и прореживанием вдвое. Второй, детализирующий, возникает при наложении вейвлет-фильтра, то есть коэффициентов gk, и при прореживании вдвое. Для последующих разложений сигнала по уровням входом является аппроксимирующий сигнал.
Продолжительность процесса разложения зависит от длины начальных данных N и заданного уровня разложения.
Быстрое вейвлет-преобразование, или алгоритм Малла, можно реализовать с помощью умножения матрицы преобразования, составленной из коэффициентов масштабирующей функции, на вектор-столбец входных данных длины N. Матрица преобразования составляется следующим образом (для простоты возьмем вейвлет Добеши второго порядка – четырехточечный вейвлет).
Нечетные строки составляются из коэффициентов hk – h0, h1, h2, h3, то есть первые четыре элемента строки являются коэффициентами фильтра, остальные зануляются. Для каждой последующей нечетной строки коэффициенты hk сдвигаются циклически влево на величину порядка вейвлета, в данном случае на 2.
Четные строки составляются из коэффициентов gk, порядок которых по формуле (9) таков – h3, -h2, h1, -h0. Для каждой последующей четной строки коэффициенты gk сдвигаются аналогично на величину порядка вейвлета.
Матрица преобразования будет выглядеть следующим образом:
|
h0
|
h1
|
h2
|
h3
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
|
h3
|
-h2
|
h1
|
-h0
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
|
0
|
0
|
h0
|
h1
|
h2
|
h3
|
…
|
0
|
0
|
0
|
0
|
|
0
|
0
|
h3
|
-h2
|
h1
|
-h0
|
…
|
0
|
0
|
0
|
0
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
…
|
h0
|
h1
|
h2
|
h3
|
|
0
|
0
|
0
|
0
|
0
|
0
|
…
|
h3
|
-h2
|
h1
|
h3
|
|
h2
|
h3
|
0
|
0
|
0
|
0
|
…
|
0
|
0
|
h0
|
h1
|
|
h1
|
-h0
|
0
|
0
|
0
|
0
|
…
|
0
|
0
|
h3
|
-h2
|
При умножении каждой нечетной строки на элемент вектора-столбца исходных данных будем получать аппроксимирующий коэффициент, в случае четных строк – детализирующий. Таким образом, операция вейвлет-разложения сведется к умножению матрицы фильтра размером N´N на вектор-столбец данных размером N. Эти операции есть не что иное, как два связных свертывания и прореживание вдвое. Для восстановления сигнала следует транспонировать матрицу преобразования и умножить на вектор-столбец, составленный из аппроксимирующих и детализирующих коэффициентов.
Число операций для вейвлет-преобразования не превышает числа операций для быстрого преобразования Фурье [3].
Алгоритм нахождения коэффициентов для любого натурального порядка вейвлета подробно описан в [2].
Предложенный в данной статье алгоритм можно эффективно запрограммировать на компьютере. Для этого необходимо следующее.
1. Помимо вычисления коэффициентов hk, нужно заранее вычислять коэффициенты gk. Это позволит сократить вычислительные операции.
2. Набор коэффициентов можно умножить на константу на этапе предвычислений. Это связано с тем, что существует стандартное значение для параметра в кратномасштабном анализе, равное 2.
3. Избегать неявных преобразований чисел. Например, на платформе .Net определен оператор умножения чисел типа int и double. Следовательно, если данные будут типа double, удастся избежать потери производительности, связанной с неявным преобразованием типов.
4. Создавать многопоточный код. Вейвлет-преобразование свелось к элементарному умножению матрицы на вектор. Данная задача легко распараллеливается, например, каждый поток будет высчитывать свой коэффициент. Число потоков зависит от числа ядер на процессоре. Обычный пользователь имеет 2 или 4 ядра на своем компьютере. Код должен использовать не менее четырех потоков для максимально быстрого выполнения на рядовом компьютере.
5. Использовать графические процессоры, например NVidia Сuda. Задача отлично распараллеливается, и на нее не распространяются ограничения платформы CUDA. Ожидается повышение производительности на графических процессорах на порядок (http://benchmarkreviews.com/index.php?option=com_content&task=view&id=187&Itemid=1).
 Описанный алгоритм был реализован на платформе .Net.
Описанный алгоритм был реализован на платформе .Net.
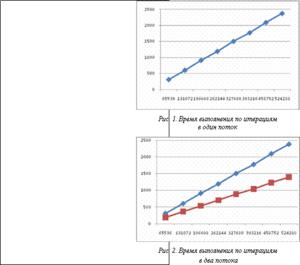
Графики зависимости времени выполнения от количества итераций приведены на рисунках 1 и 2 (просчитывалось на процессоре Intel Core 2 Duo E7300 с тактовой частотой в 2,53 МГц). По оси абсцисс откладывается количество отсчетов в сигнале, по оси ординат – суммарное время выполнения прямого и обратного вейвлет-преобразований первого уровня в миллисекундах.
Количество отсчетов сигнала в секунду зависит от частоты выборки при записи звукового сигнала. Частота дискретизации показывает, насколько более точно передан сигнал в цифровом виде. Для записи музыки используют частоту дискретизации 44100 или 48000 Гц. Человеческий голос можно записывать с меньшей частотой – 4000–8000 Гц без ощутимой потери качества. Таким образом, вейвлет-преобразование сигнала длительностью в одну секунду с частотой дискретизации в 8000 Гц будет выполняться 45 мс на одноядерном процессоре и менее 30 мс на двухъ- ядерном. Таким образом, во время вейвлет-преобразования нагрузка на процесс будет менее 5 %. Это позволяет сделать вывод о том, что описанная реализация может применяться для задач, использующих вейвлет-преобразования, в режиме реального времени на достаточно нетребовательном компьютере либо на мобильной платформе.
Литература
1. Яковлев А.Н. Введение в вейвлет-преобразования: учеб. пособие. Новосибирск: Изд-во НГТУ, 2003. 104 с.
2. Давыдов А.В. Вейвлетные преобразования сигналов: курс лекций. URL: http://prodav.narod.ru/wavelet/ (дата обращения: 01.12.2010).
3. Введение в вейвлет-анализ: учеб.-практич. пособие / М.Н. Юдин, Ю.А. Фарков, Д.М. Филатов. М.: Моск. геологоразв. акад., 2001. 72 с.



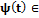
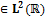 с нулевым средним значением
с нулевым средним значением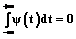 . (1)
. (1)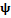 на величину m и сдвига на k получаем семейство таких функций (см. [1]):
на величину m и сдвига на k получаем семейство таких функций (см. [1]):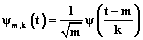 . (2)
. (2)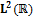 можно описать через иерархические вложенные подпространства VmÌ
можно описать через иерархические вложенные подпространства VmÌ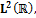 m=0, ±1, ±2, …, которые не пересекаются, а их объединение в пределе дает
m=0, ±1, ±2, …, которые не пересекаются, а их объединение в пределе дает 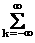 Cm,kjk(t)+
Cm,kjk(t)+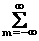
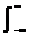 s(t)jmk(t) dt, (5)
s(t)jmk(t) dt, (5) s(t)ymk(t)dt . (6)
s(t)ymk(t)dt . (6)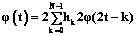 , (7)
, (7) (8)
(8) , (9)
, (9)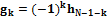 , (10)
, (10)
