При исследовании широкого круга проблем, связанных с моделированием и параметризацией диагностических тестов [1], необходимо иметь модель дихотомической матрицы результатов тестирования, используя которую, можно было бы оценить генеральные значения βj и θi латентных параметров однопараметрической дихотомической модели Раша [2, 3]. Элементы такой матрицы должны соответствовать модели Раша, используемой в качестве модели измерения латентных параметров β и θ, а статистические параметры удовлетворять критериям качества виртуального теста-модели, результаты выполнения которого эти элементы матрицы представляют. Строки модели-матрицы – это совокупности нулей и единиц, оценивающие выполнение виртуального набора индикаторов каждым из виртуальных участников тестирования, а ее столбцы – результаты выполнения каждого из индикаторов каждым из участников. Суммирование элементов модели-матрицы по строкам позволяет получить значения индивидуальных баллов xi участников тестирования, а сложение значений элементов столбцов модели-матрицы – значения индивидуальных баллов yi индикаторов. В соответствии с рекуррентными формулами, используемыми для расчета значений латентных параметров модели Раша, именно на основе этих индивидуальных баллов участников тестирования и заданий оцениваются генеральные значения θi и βj латентных параметров [1, 3].
В общем случае генеральная дихотомическая матрица результатов тестирования должна иметь достаточно много строк и столбцов. Количество строк определяет объем необходимой виртуальной выборки студентов, что проблемой не является (по крайней мере в общем случае). Количество столбцов – это число виртуальных индикаторов диагностического теста-модели, на практике ограниченное разумными пределами. Например, рекомендуется включать в педагогический тест 50 заданий. Увеличение количества заданий сверх этой цифры приводит к утомляемости участников тестирования, поэтому полученные значения θi и βj в этом случае нельзя считать объективными [3]. С учетом данного обстоятельства формируемая матрица ответов может содержать достаточно большое количество строк и ограниченное число индикаторов L (L≈50). В связи с этим под термином «генеральная модель» будем понимать модель дихотомической матрицы с достаточно большим количеством строк и ограниченным количеством столбцов, по которым рассчитываются генеральные значения θi и βj латентных параметров, из нее формируются подматрицы для решения задач, связанных с моделированием и параметризацией педагогических тестов.
Ограничение числа индикаторов привносит определенные трудности в процесс создания генеральной дихотомической матрицы. Поскольку значения индивидуальных баллов xi могут быть только целочисленными, ограничение числа индикаторов, с одной стороны, усложняет обеспечение нормативности матрицы ответов, с другой – снижает точность расчетной оценки латентного параметра θi .
Понятие нормативности для экспериментальной дихотомической матрицы результатов означает, что в ней участники тестирования с разным уровнем подготовленности θ представлены в тех же пропорциях, что и в генеральной матрице ответов. Если же говорить о дихотомической матрице ответов, используемой для расчета генеральных значений θi и βj, то для нее выполнение требования нормативности означает одновременное соблюдение двух условий.
1. Все индикаторы теста-модели должны быть разной трудности. Расположение их на оси латентной переменной β должно соответствовать статистической плотности распределения вероятности ρβ значений βj. Если это нормальное распределение, то в его центральной части значения βj должны располагаться гуще, при удалении от центра – реже.
2. Плотность расположения всех N участников тестирования на оси латентной переменной θ должна соответствовать распределению, определяемому законом распределения плотности вероятности ρθ значений θi. Среди них обязательно наличие участников с одинаковыми значениями θi, причем их число ni должно соответствовать распределению плотности вероятности ρθ. В выборке должны присутствовать только те участники тестирования, уровень подготовленности которых соответствует целочисленным значениям xi, изменяющимся в диапазоне от 1 до L-1.
Формирование модели дихотомической матрицы результатов тестирования
На первом этапе формирования модели матрицы выбираются законы распределения значений латентных переменных θi и βj. Как показывает опыт массовой обработки результатов централизованного тестирования, ЕГЭ, а также обработки результатов тестирования уровня подготовленности студентов многоуровневого университетского комплекса «ЮРГУЭС» (г. Шахты), статистики θi и βj распределены по нормальному закону [3]. Поэтому при формировании модели дихотомической матрицы ответов предполагалось, что значения θi и βj подчинены нормальному закону распределения с плотностями ρθ и ρβ соответственно:
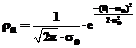 , (1) , (1)
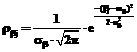 . (2) . (2)
На втором этапе оцениваются интервалы изменения переменных θi и βj. Чтобы обеспечить валидность теста-модели по отношению к виртуальной генеральной выборке студентов, интервалы изменения θi и βi желательно выбирать одинаковыми, равными [-a; a].
Задавая числа интервалов разбиения выбранного диапазона изменения переменных θi и βi равными νθ и νβ, находим длину частичных интервалов Δθ и Δβ:
 , (3) , (3)
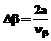 , (4) , (4)
где числа νθ и νβ должны быть нечетными.
Задаем значения параметров mθ, σθ и mβ, σβ законов распределения плотности вероятности θi и βj. Используя значения mθ и mβ в качестве центров распределений, определяем границы интервалов разбиения диапазонов изменения для θ и β.
Находим число участников тестирования nν в каждом интервале разбиения. Для k-го интервала формула для вычисления nk будет иметь вид
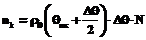 , (5) , (5)
где θнк – нижняя граница k-го интервала; ρθ(θ) – плотность распределения вероятности латентной переменной θ. Рассчитываем значения уровня подготовленности участников тестирования по интервалам. Для k-го интервала разбиения расчетное выражение имеет вид
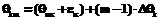 , ( , (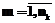 , , 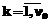 ), ),
где 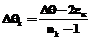 , eк – малая величина, наличие которой исключает попадание значений θkm на границу интервала. Полученные значения θkm объединяем в одну общую выборку , eк – малая величина, наличие которой исключает попадание значений θkm на границу интервала. Полученные значения θkm объединяем в одну общую выборку  ( (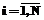 ; ;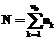 ), элементы которой будут упорядочены по возрастанию уровня подготовленности участников тестирования от 1-го к N-му (в модели-матрице они расположены сверху вниз). ), элементы которой будут упорядочены по возрастанию уровня подготовленности участников тестирования от 1-го к N-му (в модели-матрице они расположены сверху вниз).
Рассчитываем число lν индикаторов в каждом интервале разбиения. Для s-го интервала оно определится выражением
 , (6) , (6)
где βнs – нижняя граница s-го интервала; ρβ(β) – функция плотности распределения вероятности латентной переменной β.
Определяем значения βsm уровня трудности индикаторов для s-го интервала разбиения:
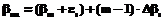 , ( , (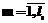 , , 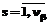 ), ),
где 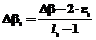 , βнs – нижняя граница интервала; es – малая величина, использование которой исключает попадание значений βsm на границы интервала. Объединяя полученные значения βsm, получим выборку , βнs – нижняя граница интервала; es – малая величина, использование которой исключает попадание значений βsm на границы интервала. Объединяя полученные значения βsm, получим выборку 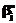 ( (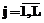 , , 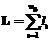 ), элементы которой упорядочены по возрастанию значений трудности от 1-го к L-му (в модели-матрице они будут расположены слева направо). ), элементы которой упорядочены по возрастанию значений трудности от 1-го к L-му (в модели-матрице они будут расположены слева направо).
Используя найденные выборки  и и 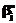 и выражение для модели Раша, находим индивидуальные баллы и выражение для модели Раша, находим индивидуальные баллы 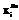 и и 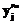 : :
 , , 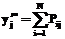 , (7) , (7)
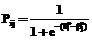 . .
Округляем полученные значения 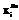 и и 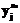 до целочисленных xi и yj. Проверяем выполнение равенства до целочисленных xi и yj. Проверяем выполнение равенства
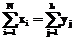 . (8) . (8)
Если равенство не выполняется, корректируем значения xi и yj за счет изменения числа участников тестирования N.
По найденным значениям xi и yj формируется первоначальная модель дихотомической матрицы результатов тестирования M0. Поскольку элементы выборки 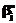 упорядочены по возрастанию значений слева направо, а выборки упорядочены по возрастанию значений слева направо, а выборки  – сверху вниз, результаты выполнения наиболее трудных индикаторов будут располагаться в крайних правых столбцах матрицы, а результаты ответов на индикаторы наиболее подготовленных студентов – в самых нижних строках матрицы. Заполнение матрицы элементами «1» целесообразно начинать с ее правой нижней части. Единицы должны быть распределены по ячейкам матрицы M0 таким образом, чтобы сумма их по каждой строке была равна соответствующему индивидуальному баллу xi участника тестирования с номером i, а сумма единиц по каждому столбцу – индивидуальному баллу yj задания под номером j. Заполнение матрицы единицами осуществлялось справа налево, снизу вверх. После расстановки единиц пустые ячейки матрицы заполняются нулями, и получается первичная (предварительная) модель матрицы M0. На этом заканчивается первый этап формирования модели генеральной дихотомической матрицы результатов тестирования. – сверху вниз, результаты выполнения наиболее трудных индикаторов будут располагаться в крайних правых столбцах матрицы, а результаты ответов на индикаторы наиболее подготовленных студентов – в самых нижних строках матрицы. Заполнение матрицы элементами «1» целесообразно начинать с ее правой нижней части. Единицы должны быть распределены по ячейкам матрицы M0 таким образом, чтобы сумма их по каждой строке была равна соответствующему индивидуальному баллу xi участника тестирования с номером i, а сумма единиц по каждому столбцу – индивидуальному баллу yj задания под номером j. Заполнение матрицы единицами осуществлялось справа налево, снизу вверх. После расстановки единиц пустые ячейки матрицы заполняются нулями, и получается первичная (предварительная) модель матрицы M0. На этом заканчивается первый этап формирования модели генеральной дихотомической матрицы результатов тестирования.
На втором этапе обеспечиваются адекватность элементов матрицы M0 модели Раша, а также соответствие системообразующих свойств индикаторов и их критериальной валидности научно обоснованным критериям качества. При заданных значениях индивидуальных баллов xi и yj элементы матрицы M0 необходимо расположить таким образом, чтобы они были адекватны модели Раша, обладали требуемыми системообразующими свойствами и критериальной валидностью.
В современных программных средствах адекватность проверяется, как правило, на основе критерия согласия c2. Адекватность считается обеспеченной, если вероятности 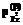 и и 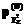 соответствия модели Раша индивидуальных баллов всей совокупности индикаторов и всех участников тестирования в целом равны 1 или близки к 1. Это условие должно выполняться также для каждого индикатора и для каждого тестируемого в отдельности. соответствия модели Раша индивидуальных баллов всей совокупности индикаторов и всех участников тестирования в целом равны 1 или близки к 1. Это условие должно выполняться также для каждого индикатора и для каждого тестируемого в отдельности.
Второй этап начинают с проверки адекватности полученной матрицы M0, для чего она обрабатывается с помощью программных средств, реализующих дихотомическую модель Раша, например, с помощью программного комплекса RILP-1 [4], и анализируются полученные значения вероят- ностей согласия 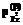 и и 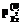 . Как правило, их первоначальные значения близки к нулю. Для повышения . Как правило, их первоначальные значения близки к нулю. Для повышения 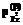 и и  случайным образом осуществляются перестановки нулей и единиц в парах столбцов или строк, и каждый раз проверяется, как меняются значения случайным образом осуществляются перестановки нулей и единиц в парах столбцов или строк, и каждый раз проверяется, как меняются значения 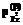 и и 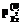 . При их возрастании изменения в матрице сохраняются. Процесс перестановки повторяется до тех пор, пока каждое из значений . При их возрастании изменения в матрице сохраняются. Процесс перестановки повторяется до тех пор, пока каждое из значений 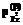 и и  не приблизится к едини- це. Как показал эксперимент, при достижении адекватности автоматически обеспечиваются необходимые значения (Rbj>0,3) точечного бисериального коэффициента корреляции Rbj, характеризующего критериальную валидность индикаторов, а также их коэффициентов интеркорреляции rij, определяющих системообразующие свойства всей совокупности индикаторов. не приблизится к едини- це. Как показал эксперимент, при достижении адекватности автоматически обеспечиваются необходимые значения (Rbj>0,3) точечного бисериального коэффициента корреляции Rbj, характеризующего критериальную валидность индикаторов, а также их коэффициентов интеркорреляции rij, определяющих системообразующие свойства всей совокупности индикаторов.
Таким образом, после обеспечения адекватности индикаторов и участников тестирования модели измерения Раша получается модель генеральной дихотомической матрицы ответов M в окончательном виде.
Рассчитанные по матрице M значения латентных переменных 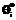 и и 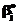 могут отличаться от значений могут отличаться от значений  и и 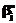 , которые изначально выбирались как оценки генеральных. Это обусловлено тем, что , которые изначально выбирались как оценки генеральных. Это обусловлено тем, что 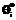 и и 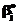 рассчитывались по округленным значениям индивидуальных баллов xi и yj, а не по рассчитывались по округленным значениям индивидуальных баллов xi и yj, а не по 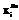 и и 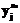 , определяемым по значениям , определяемым по значениям  и и 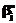 . Поэтому генеральными значениями qi и bj латентных переменных окончательно выбираем значения . Поэтому генеральными значениями qi и bj латентных переменных окончательно выбираем значения 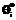 и и 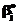 : qi= : qi=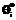 , bj= , bj=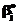 . В качестве параметров законов распределения статистик qi и bj принимаем значения, рассчитанные по сформированной матрице . В качестве параметров законов распределения статистик qi и bj принимаем значения, рассчитанные по сформированной матрице 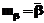 ; ;  ; ;  ; ; 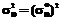 , где , где 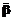 , , 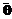 и и 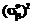 , ,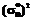 – выборочные средние и выборочные дисперсии значений – выборочные средние и выборочные дисперсии значений 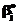 и и 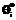 . .
На заключительном этапе проверяем соответствие законов распределения полученных значений qi и bj нормальному закону. С этой целью строим гистограммы распределения этих значений, считая центрами распределения mq и mb, с длиной интервалов разбиения, определяемых выражениями (3), (4). Проверяем выполнение критерия согласия c2 для полученных гистограмм, используя выражения (1), (2) для законов распределения плотностей вероятностей. Равенство или близость к 1 вероятностей согласия 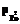 для статистики qi и для статистики qi и 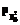 для статистики bj свидетельствует о том, что полученную модель дихотомической матрицы можно считать генеральной. Если хотя бы одна из величин для статистики bj свидетельствует о том, что полученную модель дихотомической матрицы можно считать генеральной. Если хотя бы одна из величин 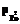 или или 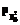 заметно отличается от 1, обрабатывают полученную матрицу и анализируют расположение характеристических кривых индикаторов и персональных кривых участников тестирования на осях латентных переменных. Снижение величины заметно отличается от 1, обрабатывают полученную матрицу и анализируют расположение характеристических кривых индикаторов и персональных кривых участников тестирования на осях латентных переменных. Снижение величины 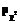 возникает, как правило, из-за отклонений плотности распределения указанных кривых на этих осях от нормального закона. То есть из-за нарушения условия нормативности сформированной матрицы. Для ее восстановления корректируют расположение кривых на осях латентных переменных, изменяя значения xi или yj. возникает, как правило, из-за отклонений плотности распределения указанных кривых на этих осях от нормального закона. То есть из-за нарушения условия нормативности сформированной матрицы. Для ее восстановления корректируют расположение кривых на осях латентных переменных, изменяя значения xi или yj.
Проведение вычислительного эксперимента
Первоначальным планом вычислительного эксперимента предусматривалось формирование модели дихотомической матрицы с числом индикаторов L=51 и числом участников тестирования N=1020. Значение индивидуального балла xi при заданном числе индикаторов может изменяться в пределах от 1 до 50. В первом приближении это соответствует изменению уровня подготовленности q участников тестирования в интервале от минус 3,912 до 3,912 логит. Конкретные первоначальные значения латентного параметра q рассчитывались по значениям xi в предположении, что они изменяются в диапазоне от 1 до 50 с шагом Δx=1. Для расчета использовалась формула 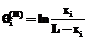 . .
Полученные значения 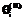 представлены в столбце 4 таблицы 1. Значения представлены в столбце 4 таблицы 1. Значения  рассчитывались по формуле рассчитывались по формуле 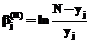 . .
Диапазон их изменения выбирался таким же, как и для значений 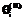 . .
Рассчитанные значения  приведены в столбце 2 таблицы 1. Исходные значения оценок математических ожиданий приведены в столбце 2 таблицы 1. Исходные значения оценок математических ожиданий 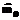 и и 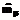 выбирались равными 0. Первоначальные оценки стандартных отклонений выбирались равными 0. Первоначальные оценки стандартных отклонений 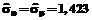 рассчитывались исходя из правила трех сигм, характерного для нормального закона распределения. рассчитывались исходя из правила трех сигм, характерного для нормального закона распределения.
Таблица 1
Данные для формирования первичной модели матрицы
|
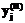
|

|
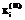
|
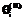
|
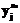
|
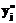
|
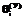
|
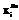
|

|
|
20
|
3,9120
|
1
|
-3,9120
|
|
|
-3,912
|
2,21
|
2
|
|
40
|
3,1987
|
2
|
-3,1987
|
929,53
|
930
|
-3,1987
|
3,97
|
4
|
|
60
|
2,7726
|
3
|
-2,7726
|
899,41
|
899
|
-2,7726
|
5,48
|
5
|
|
80
|
2,4639
|
4
|
-2,4639
|
872,40
|
872
|
-2,4639
|
6,82
|
7
|
|
100
|
2,2192
|
5
|
-2,2192
|
847,65
|
848
|
-2,2192
|
8,03
|
8
|
|
125
|
2,0149
|
6
|
-2,0149
|
824,66
|
825
|
-2,0149
|
9,15
|
9
|
|
140
|
1,8383
|
7
|
-1,8383
|
803,07
|
803
|
-1,8383
|
10,20
|
10
|
|
160
|
1,6818
|
8
|
-1,6818
|
782,62
|
783
|
-1,6818
|
11,19
|
11
|
|
180
|
1,5404
|
9
|
-1,5404
|
763,13
|
763
|
-1,5404
|
12,13
|
12
|
|
200
|
1,4110
|
10
|
-1,4110
|
744,45
|
744
|
-1,4110
|
13,02
|
13
|
|
220
|
1,2910
|
11
|
-1,2910
|
726,46
|
726
|
-1,2910
|
13,89
|
14
|
|
240
|
1,1787
|
12
|
-1,1787
|
709,06
|
709
|
-1,1787
|
14,72
|
15
|
|
260
|
1,0726
|
13
|
-1,0726
|
692,17
|
692
|
-1,0726
|
15,53
|
16
|
|
280
|
0,9719
|
14
|
-0,9719
|
675,72
|
676
|
-0,9719
|
16,31
|
16
|
|
300
|
0,8755
|
15
|
-0,8755
|
659,66
|
660
|
-0,8755
|
17,08
|
17
|
|
320
|
0,7828
|
16
|
-0,7828
|
643,94
|
644
|
-0,7828
|
17,83
|
18
|
|
340
|
0,6931
|
17
|
-0,6931
|
628,50
|
629
|
-0,6931
|
18,57
|
19
|
|
360
|
0,6061
|
18
|
-0,6061
|
613,31
|
613
|
-0,6061
|
19,29
|
19
|
|
380
|
0,5213
|
19
|
-0,5213
|
598,33
|
598
|
-0,5213
|
20,01
|
20
|
|
400
|
0,4383
|
20
|
-0,4383
|
583,53
|
584
|
-0,4383
|
20,71
|
21
|
|
420
|
0,3567
|
21
|
-0,3567
|
568,88
|
569
|
-0,3567
|
21,41
|
21
|
|
440
|
0,2763
|
22
|
-0,2763
|
554,34
|
554
|
-0,2763
|
22,10
|
22
|
|
460
|
0,1967
|
23
|
-0,1967
|
539,90
|
540
|
-0,1967
|
22,79
|
23
|
|
480
|
0,1178
|
24
|
-0,1178
|
525,51
|
526
|
-0,1178
|
23,48
|
23
|
|
500
|
0,0392
|
25
|
-0,0392
|
511,17
|
511
|
-0,0392
|
24,16
|
24
|
|
520
|
-0,0392
|
26
|
0,0392
|
504,00
|
504
|
0,0000
|
24,85
|
25
|
|
540
|
-0,1178
|
27
|
0,1178
|
496,83
|
497
|
0,0392
|
25,00
|
25
|
|
560
|
-0,1967
|
28
|
0,1967
|
482,49
|
482
|
0,1178
|
25,53
|
26
|
|
580
|
-0,2763
|
29
|
0,2763
|
468,10
|
468
|
0,1967
|
26,22
|
26
|
|
600
|
-0,3567
|
30
|
0,3567
|
453,66
|
454
|
0,2763
|
26,91
|
27
|
|
620
|
-0,4383
|
31
|
0,4383
|
439,12
|
439
|
0,3567
|
27,60
|
28
|
|
640
|
-0,5213
|
32
|
0,5213
|
424,47
|
424
|
0,4383
|
28,30
|
28
|
|
660
|
-0,6061
|
33
|
0,6061
|
409,67
|
410
|
0,5213
|
29,00
|
29
|
|
680
|
-0,6931
|
34
|
0,6931
|
394,69
|
395
|
0,6061
|
29,72
|
30
|
|
700
|
-0,7828
|
35
|
0,7828
|
379,50
|
379
|
0,6931
|
30,44
|
30
|
|
720
|
-0,8755
|
36
|
0,8755
|
364,06
|
364
|
0,7828
|
31,18
|
31
|
|
740
|
-0,9719
|
37
|
0,9719
|
348,33
|
348
|
0,8755
|
31,93
|
32
|
|
760
|
-1,0726
|
38
|
1,0726
|
332,28
|
332
|
0,9719
|
32,70
|
33
|
|
780
|
-1,1787
|
39
|
1,1787
|
315,83
|
316
|
1,0726
|
33,48
|
33
|
|
800
|
-1,2910
|
40
|
1,2910
|
298,94
|
299
|
1,1787
|
34,29
|
34
|
|
820
|
-1,4110
|
41
|
1,4110
|
281,54
|
282
|
1,2910
|
35,12
|
35
|
|
840
|
-1,5404
|
42
|
1,5404
|
263,55
|
264
|
1,4110
|
35,99
|
36
|
|
860
|
-1,6818
|
43
|
1,6818
|
244,87
|
245
|
1,5404
|
36,89
|
37
|
|
880
|
-1,8383
|
44
|
1,8383
|
225,38
|
225
|
1,6818
|
37,82
|
38
|
|
900
|
-2,0149
|
45
|
2,0149
|
204,93
|
205
|
1,8383
|
38,81
|
39
|
|
920
|
-2,2192
|
46
|
2,2192
|
188,86
|
189
|
1,9685
|
39,86
|
40
|
|
940
|
-2,4639
|
47
|
2,4639
|
160,35
|
160
|
2,2192
|
40,98
|
41
|
|
960
|
-2,7726
|
48
|
2,7726
|
135,60
|
136
|
2,4639
|
42,19
|
42
|
|
980
|
-3,1987
|
49
|
3,1987
|
108,59
|
109
|
2,7726
|
43,53
|
44
|
|
1000
|
-3,9120
|
50
|
3,9120
|
78,47
|
78
|
3,1987
|
45,03
|
45
|
| |
|
|
|
|
|
3,912
|
46,95
|
47
|
Для нахождения числа тестируемых по интервалам разбиения 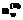 и тестируемых с одинаковым уровнем знаний ni строилась гистограмма распределения значений и тестируемых с одинаковым уровнем знаний ni строилась гистограмма распределения значений 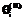 . Для этого выбранный диапазон варьирования латентных переменных разбивался на несколько интервалов. С учетом рассчитанных значений . Для этого выбранный диапазон варьирования латентных переменных разбивался на несколько интервалов. С учетом рассчитанных значений 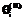 ширина интервала разбиения Δθ выбиралась равной 0,8 логит. Поскольку число интервалов vq должно быть нечетным, диапазон изменения латентных переменных был расширен до [-4,4; 4,4] логит. После этого значение vq оказалось равным 11. Первый интервал разбиения располагался симметрично относительно центра распределения ширина интервала разбиения Δθ выбиралась равной 0,8 логит. Поскольку число интервалов vq должно быть нечетным, диапазон изменения латентных переменных был расширен до [-4,4; 4,4] логит. После этого значение vq оказалось равным 11. Первый интервал разбиения располагался симметрично относительно центра распределения 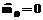 . Для расчета числа участников . Для расчета числа участников 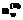 в каждом интервале разбиения использовалась формула (5). Значения в каждом интервале разбиения использовалась формула (5). Значения 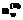 для интервалов слева направо составили: 5, 18, 58, 126, 194, 218, 194, 126, 58, 18, 5. По ним построена гистограмма распределения, и с помощью критерия согласия c2 проверено ее соответствие нормальному закону распределения. Значение вероятности согласия для интервалов слева направо составили: 5, 18, 58, 126, 194, 218, 194, 126, 58, 18, 5. По ним построена гистограмма распределения, и с помощью критерия согласия c2 проверено ее соответствие нормальному закону распределения. Значение вероятности согласия 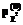 оказалось близким к 1. оказалось близким к 1.
Аналогичные процедуры были проделаны для значений  в предположении, что Δβ=Δθ=0,8 логит, vβ=vθ=11. При построении гистограммы значения βj не повторялись. Значения в предположении, что Δβ=Δθ=0,8 логит, vβ=vθ=11. При построении гистограммы значения βj не повторялись. Значения 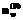 для двух крайних интервалов оказались равными 0,263. Поскольку для двух крайних интервалов оказались равными 0,263. Поскольку 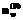 может принимать только целочисленные значения и рассчитанные значения может принимать только целочисленные значения и рассчитанные значения  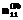 =0,263 намного меньше 1, число разбиений vβ пришлось уменьшить, отбросив два крайних интервала. Поэтому число заданий сократилось до 49. Их распределение по интервалам разбиения составило 1, 3, 6, 9, 11, 9, 6, 3, 1. Проверка показала, что полученная гистограмма распределения значений =0,263 намного меньше 1, число разбиений vβ пришлось уменьшить, отбросив два крайних интервала. Поэтому число заданий сократилось до 49. Их распределение по интервалам разбиения составило 1, 3, 6, 9, 11, 9, 6, 3, 1. Проверка показала, что полученная гистограмма распределения значений  соответствует нормальному закону распределения с вероятностью согласия соответствует нормальному закону распределения с вероятностью согласия 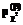 , очень близкой к 1. , очень близкой к 1.
По найденным значениям 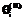 и и  с помощью формул (7) рассчитаны значения индивидуальных баллов с помощью формул (7) рассчитаны значения индивидуальных баллов 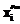 и и 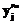 (столбцы 5, 8 табл. 1), которые были округлены до целочисленных значений (столбцы 5, 8 табл. 1), которые были округлены до целочисленных значений  и и  (столбцы 6, 9 табл. 1). Проверялось выполнение равенства (столбцы 6, 9 табл. 1). Проверялось выполнение равенства  . Для его достижения пришлось снизить число участников тестирования до 1008. . Для его достижения пришлось снизить число участников тестирования до 1008.
Далее по значениям  и и  сформирована модель дихотомической матрицы М0, как было описано выше. Обработка полученной матрицы программным комплексом RILP-1M позволила уточнить значение оценки стандартного отклонения сформирована модель дихотомической матрицы М0, как было описано выше. Обработка полученной матрицы программным комплексом RILP-1M позволила уточнить значение оценки стандартного отклонения 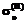 для латентного параметра q. Она оказалась равной для латентного параметра q. Она оказалась равной 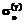 =1,407 логит. С использованием этого значения =1,407 логит. С использованием этого значения 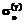 пересчитывались ранее полученные пересчитывались ранее полученные 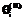 и находились новые и находились новые  . По значениям . По значениям  , которые оставлялись неизменными, и , которые оставлялись неизменными, и  рассчитывались новые значения рассчитывались новые значения 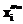 и и  , округляемые до целочисленных величин xi и yj. Для обеспечения выполнения условия (8) число участников тестирования пришлось увеличить до 1009. По значениям xi и yj была сформирована новая модель дихотомической матрицы М1. Изменением расположения ее элементов при неизменных значениях xi и yj обеспечивались их адекватность модели Раша, необходимые системообразующие свойства индикаторов и их критериальная валидность. В результате была получена окончательная модель генеральной дихотомической матрицы М. , округляемые до целочисленных величин xi и yj. Для обеспечения выполнения условия (8) число участников тестирования пришлось увеличить до 1009. По значениям xi и yj была сформирована новая модель дихотомической матрицы М1. Изменением расположения ее элементов при неизменных значениях xi и yj обеспечивались их адекватность модели Раша, необходимые системообразующие свойства индикаторов и их критериальная валидность. В результате была получена окончательная модель генеральной дихотомической матрицы М.
Параметры латентных переменных θ и β, а также величины, характеризующие показатели качества теста-модели, рассчитанные с помощью программного комплекса RILP-1M по сформированной модели матрицы, приведены в таблицах 2 и 3.
Таблица 2
Статистические параметры теста-модели
|
mθ, логит
|
m β, логит
|
σθ, логит
|
σβ, логит
|
rd
|
αKr
|
rSB
|
rnt
|
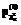
|
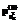
|
|
0,004
|
0,000
|
1,414
|
1,453
|
0,926
|
0,929
|
0,926
|
0,933
|
1,0
|
0,999
|
Из таблицы 2 видно, что статистические показатели, характеризующие качество теста-модели, являются высокими. Коэффициент дифференциации участников тестирования составил 0,926. Значения коэффициента надежности, рассчитанные разными методами, оказались больше 0,9 и составили:
– 0,929 для метода Кронбаха (α Кронбаха);
– 0,926 для метода Спирмана–Брауна (он же характеризует гомогенность теста-модели);
– 0,934 для метода, основанного на использовании среднего значения коэффициента интеркорреляции индикаторов.
Адекватность совокупности индикаторов и всех тестируемых в целом модели Раша является высокой: вероятности соответствия результатов выполнения индикаторов их теоретическим характеристическим кривым и теоретическим персональным кривым участников составляют соответственно 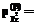 0,999 и 0,999 и  1,0 (последние столбцы табл. 2). Анализ значений коэффициентов интеркорреляции индикаторов rij показал, что все они положительные и не превышают 0,3, а это является свидетельством соответствия их системообразующих свойств принятым критериям [5]. 1,0 (последние столбцы табл. 2). Анализ значений коэффициентов интеркорреляции индикаторов rij показал, что все они положительные и не превышают 0,3, а это является свидетельством соответствия их системообразующих свойств принятым критериям [5].
В столбце 3 таблицы 3 приведены значения вероятности  для каждого индикатора в отдельности. Видно, что они составляют не менее 0,4, что говорит о допустимости гипотезы об адекватности модели Раша каждого индикатора в отдельности. Аналогичный вывод справедлив и для участников тестирования. Из анализа значений бисериального коэффициента корреляции Rb (последний столбец таблицы 3) видно, что они составляют не менее 0,3, что говорит о соответствии критериальной валидности индикаторов теста-модели принятым критериям [5]. для каждого индикатора в отдельности. Видно, что они составляют не менее 0,4, что говорит о допустимости гипотезы об адекватности модели Раша каждого индикатора в отдельности. Аналогичный вывод справедлив и для участников тестирования. Из анализа значений бисериального коэффициента корреляции Rb (последний столбец таблицы 3) видно, что они составляют не менее 0,3, что говорит о соответствии критериальной валидности индикаторов теста-модели принятым критериям [5].
Таблица 3
Параметры индикаторов
|
j
|
bj логит
|
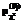
|
Rb
|
|
1
|
-3,173
|
0,499
|
0,31
|
|
2
|
-2,751
|
0,597
|
0,318
|
|
3
|
-2,444
|
0,614
|
0,352
|
|
4
|
-2,198
|
0,69
|
0,4
|
|
5
|
-1,994
|
0,64
|
0,402
|
|
6
|
-1,823
|
0,648
|
0,436
|
|
7
|
-1,663
|
0,602
|
0,44
|
|
8
|
-1,526
|
0,68
|
0,458
|
|
9
|
-1,396
|
0,629
|
0,474
|
|
10
|
-1,276
|
0,654
|
0,479
|
|
11
|
-1,167
|
0,599
|
0,483
|
|
12
|
-1,061
|
0,575
|
0,499
|
|
13
|
-0,964
|
0,539
|
0,508
|
|
14
|
-0,869
|
0,6
|
0,504
|
|
15
|
-0,775
|
0,492
|
0,51
|
|
16
|
-0,689
|
0,558
|
0,506
|
|
17
|
-0,598
|
0,509
|
0,527
|
|
18
|
-0,514
|
0,5
|
0,526
|
|
19
|
-0,436
|
0,41
|
0,513
|
|
20
|
-0,353
|
0,447
|
0,52
|
|
21
|
-0,271
|
0,448
|
0,535
|
|
22
|
-0,195
|
0,483
|
0,515
|
|
23
|
-0,114
|
0,47
|
0,529
|
|
24
|
-0,038
|
0,487
|
0,501
|
|
25
|
0
|
0,442
|
0,525
|
|
26
|
0,038
|
0,465
|
0,524
|
|
27
|
0,119
|
0,402
|
0,535
|
|
28
|
0,195
|
0,42
|
0,511
|
|
29
|
0,277
|
0,459
|
0,524
|
|
30
|
0,354
|
0,462
|
0,522
|
|
31
|
0,436
|
0,491
|
0,521
|
|
32
|
0,52
|
0,482
|
0,514
|
|
33
|
0,604
|
0,497
|
0,518
|
|
34
|
0,689
|
0,475
|
0,523
|
|
35
|
0,775
|
0,608
|
0,509
|
|
36
|
0,869
|
0,585
|
0,504
|
|
37
|
0,964
|
0,519
|
0,511
|
|
38
|
1,061
|
0,556
|
0,505
|
|
39
|
1,167
|
0,577
|
0,491
|
|
40
|
1,282
|
0,651
|
0,478
|
|
41
|
1,402
|
0,553
|
0,467
|
|
42
|
1,526
|
0,637
|
0,479
|
|
43
|
1,67
|
0,596
|
0,454
|
|
44
|
1,823
|
0,671
|
0,428
|
|
45
|
1,952
|
0,663
|
0,429
|
|
46
|
2,206
|
0,693
|
0,4
|
|
47
|
2,442
|
0,603
|
0,363
|
|
48
|
2,749
|
0,603
|
0,36
|
|
49
|
3,169
|
0,495
|
0,306
|
На рисунках 1 и 2 изображены гистограммы распределения значений qi и bj, а также кривые плотности вероятности нормального закона распределения, полученные с использованием статистических параметров, которые указаны в первых четырех столбцах таблицы 2. О соответствии статистик qi и bj нормальному закону распределения свидетельствуют высокие значения вероятности согласия (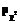 ≈1), полученные на основе критерия согласия χ2. ≈1), полученные на основе критерия согласия χ2.
На рисунке 3 показано расположение характеристических кривых индикаторов pj(θ) на оси латентной переменной θ. Визуальный анализ расположения кривых позволяет заключить, что плотность их распределения удовлетворяет нормальному закону распределения.
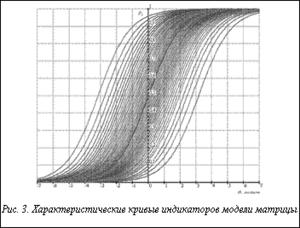  Таким образом, полученные данные свидетельствуют о том, что сформированная модель дихотомической матрицы ответов представляет собой результаты выполнения модели теста с высокими показателями качества и может считаться генеральной. Таким образом, полученные данные свидетельствуют о том, что сформированная модель дихотомической матрицы ответов представляет собой результаты выполнения модели теста с высокими показателями качества и может считаться генеральной.
Большие размеры полученной модели генеральной дихотомической матрицы ответов не позволяют привести ее в тексте статьи.
Литература
1. Нейман Ю.М., Хлебников В.А. Введение в теорию моделирования и параметризации педагогических тестов. М.: Прометей, 2000. 169 с.
2. Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen, Denmark : Danish Institute for Educational Research, 1960.
3. Елисеев И.Н. Методы, алгоритмы и программные комплексы для расчета характеристик диагностических средств независимой оценки качества образования: монография. Новочеркасск: Лик, 2010. 316 с.
4. Елисеев И.Н., Елисеев И.И., Фисунов А.В. Програм- мный комплекс RILP-1 // Программные продукты и системы. 2009. № 2. С. 178–181.
5. Аванесов В.С. Основы научной организации педагогического контроля в высшей школе. М.: Исслед. центр по пробл. управл. кач-вом подгот. спец-тов при МИСиС, 1989. 68 с.
|



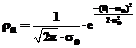 , (1)
, (1)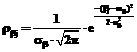 . (2)
. (2) , (3)
, (3)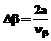 , (4)
, (4)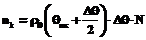 , (5)
, (5)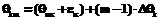 , (
, (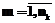 ,
, 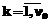 ),
),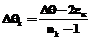 , eк – малая величина, наличие которой исключает попадание значений θkm на границу интервала. Полученные значения θkm объединяем в одну общую выборку
, eк – малая величина, наличие которой исключает попадание значений θkm на границу интервала. Полученные значения θkm объединяем в одну общую выборку  (
(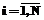 ;
;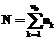 ), элементы которой будут упорядочены по возрастанию уровня подготовленности участников тестирования от 1-го к N-му (в модели-матрице они расположены сверху вниз).
), элементы которой будут упорядочены по возрастанию уровня подготовленности участников тестирования от 1-го к N-му (в модели-матрице они расположены сверху вниз). , (6)
, (6)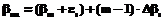 , (
, (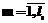 ,
, 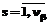 ),
),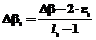 , βнs – нижняя граница интервала; es – малая величина, использование которой исключает попадание значений βsm на границы интервала. Объединяя полученные значения βsm, получим выборку
, βнs – нижняя граница интервала; es – малая величина, использование которой исключает попадание значений βsm на границы интервала. Объединяя полученные значения βsm, получим выборку 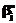 (
(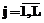 ,
, 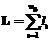 ), элементы которой упорядочены по возрастанию значений трудности от 1-го к L-му (в модели-матрице они будут расположены слева направо).
), элементы которой упорядочены по возрастанию значений трудности от 1-го к L-му (в модели-матрице они будут расположены слева направо).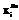 и
и 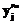 :
: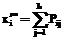 ,
, 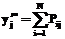 , (7)
, (7)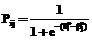 .
.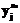 до целочисленных xi и yj. Проверяем выполнение равенства
до целочисленных xi и yj. Проверяем выполнение равенства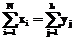 . (8)
. (8)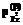 и
и 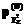 соответствия модели Раша индивидуальных баллов всей совокупности индикаторов и всех участников тестирования в целом равны 1 или близки к 1. Это условие должно выполняться также для каждого индикатора и для каждого тестируемого в отдельности.
соответствия модели Раша индивидуальных баллов всей совокупности индикаторов и всех участников тестирования в целом равны 1 или близки к 1. Это условие должно выполняться также для каждого индикатора и для каждого тестируемого в отдельности.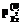 . Как правило, их первоначальные значения близки к нулю. Для повышения
. Как правило, их первоначальные значения близки к нулю. Для повышения  случайным образом осуществляются перестановки нулей и единиц в парах столбцов или строк, и каждый раз проверяется, как меняются значения
случайным образом осуществляются перестановки нулей и единиц в парах столбцов или строк, и каждый раз проверяется, как меняются значения 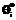 и
и 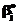 могут отличаться от значений
могут отличаться от значений 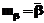 ;
;  ;
;  ;
; 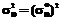 , где
, где 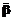 ,
, 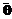 и
и 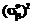 ,
,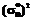 – выборочные средние и выборочные дисперсии значений
– выборочные средние и выборочные дисперсии значений 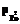 для статистики qi и
для статистики qi и 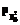 для статистики bj свидетельствует о том, что полученную модель дихотомической матрицы можно считать генеральной. Если хотя бы одна из величин
для статистики bj свидетельствует о том, что полученную модель дихотомической матрицы можно считать генеральной. Если хотя бы одна из величин 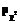 возникает, как правило, из-за отклонений плотности распределения указанных кривых на этих осях от нормального закона. То есть из-за нарушения условия нормативности сформированной матрицы. Для ее восстановления корректируют расположение кривых на осях латентных переменных, изменяя значения xi или yj.
возникает, как правило, из-за отклонений плотности распределения указанных кривых на этих осях от нормального закона. То есть из-за нарушения условия нормативности сформированной матрицы. Для ее восстановления корректируют расположение кривых на осях латентных переменных, изменяя значения xi или yj.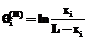 .
.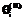 представлены в столбце 4 таблицы 1. Значения
представлены в столбце 4 таблицы 1. Значения  рассчитывались по формуле
рассчитывались по формуле 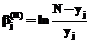 .
. и
и  выбирались равными 0. Первоначальные оценки стандартных отклонений
выбирались равными 0. Первоначальные оценки стандартных отклонений 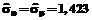 рассчитывались исходя из правила трех сигм, характерного для нормального закона распределения.
рассчитывались исходя из правила трех сигм, характерного для нормального закона распределения.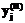
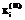
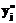
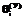

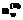 и тестируемых с одинаковым уровнем знаний ni строилась гистограмма распределения значений
и тестируемых с одинаковым уровнем знаний ni строилась гистограмма распределения значений 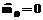 . Для расчета числа участников
. Для расчета числа участников 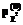 оказалось близким к 1.
оказалось близким к 1.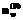 для двух крайних интервалов оказались равными 0,263. Поскольку
для двух крайних интервалов оказались равными 0,263. Поскольку 
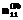 =0,263 намного меньше 1, число разбиений vβ пришлось уменьшить, отбросив два крайних интервала. Поэтому число заданий сократилось до 49. Их распределение по интервалам разбиения составило 1, 3, 6, 9, 11, 9, 6, 3, 1. Проверка показала, что полученная гистограмма распределения значений
=0,263 намного меньше 1, число разбиений vβ пришлось уменьшить, отбросив два крайних интервала. Поэтому число заданий сократилось до 49. Их распределение по интервалам разбиения составило 1, 3, 6, 9, 11, 9, 6, 3, 1. Проверка показала, что полученная гистограмма распределения значений 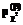 , очень близкой к 1.
, очень близкой к 1.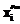 и
и  и
и  (столбцы 6, 9 табл. 1). Проверялось выполнение равенства
(столбцы 6, 9 табл. 1). Проверялось выполнение равенства  . Для его достижения пришлось снизить число участников тестирования до 1008.
. Для его достижения пришлось снизить число участников тестирования до 1008.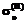 для латентного параметра q. Она оказалась равной
для латентного параметра q. Она оказалась равной 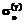 =1,407 логит. С использованием этого значения
=1,407 логит. С использованием этого значения  . По значениям
. По значениям 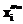 и
и  , округляемые до целочисленных величин xi и yj. Для обеспечения выполнения условия (8) число участников тестирования пришлось увеличить до 1009. По значениям xi и yj была сформирована новая модель дихотомической матрицы М1. Изменением расположения ее элементов при неизменных значениях xi и yj обеспечивались их адекватность модели Раша, необходимые системообразующие свойства индикаторов и их критериальная валидность. В результате была получена окончательная модель генеральной дихотомической матрицы М.
, округляемые до целочисленных величин xi и yj. Для обеспечения выполнения условия (8) число участников тестирования пришлось увеличить до 1009. По значениям xi и yj была сформирована новая модель дихотомической матрицы М1. Изменением расположения ее элементов при неизменных значениях xi и yj обеспечивались их адекватность модели Раша, необходимые системообразующие свойства индикаторов и их критериальная валидность. В результате была получена окончательная модель генеральной дихотомической матрицы М.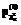
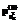
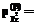 0,999 и
0,999 и  1,0 (последние столбцы табл. 2). Анализ значений коэффициентов интеркорреляции индикаторов rij показал, что все они положительные и не превышают 0,3, а это является свидетельством соответствия их системообразующих свойств принятым критериям [5].
1,0 (последние столбцы табл. 2). Анализ значений коэффициентов интеркорреляции индикаторов rij показал, что все они положительные и не превышают 0,3, а это является свидетельством соответствия их системообразующих свойств принятым критериям [5]. для каждого индикатора в отдельности. Видно, что они составляют не менее 0,4, что говорит о допустимости гипотезы об адекватности модели Раша каждого индикатора в отдельности. Аналогичный вывод справедлив и для участников тестирования. Из анализа значений бисериального коэффициента корреляции Rb (последний столбец таблицы 3) видно, что они составляют не менее 0,3, что говорит о соответствии критериальной валидности индикаторов теста-модели принятым критериям [5].
для каждого индикатора в отдельности. Видно, что они составляют не менее 0,4, что говорит о допустимости гипотезы об адекватности модели Раша каждого индикатора в отдельности. Аналогичный вывод справедлив и для участников тестирования. Из анализа значений бисериального коэффициента корреляции Rb (последний столбец таблицы 3) видно, что они составляют не менее 0,3, что говорит о соответствии критериальной валидности индикаторов теста-модели принятым критериям [5].