Одним из перспективных направлений развития моделирующих комплексов тренажной под- готовки персонала является обеспечение возможности проведения комплексных упражнений с участием двух или нескольких обучаемых операторов. Для обеспечения возможности взаимодействия тренирующихся в виртуальном мире операторов необходимо, чтобы каждый оператор, как и моделируемые системы, стал объектом моделирования. Для этого в состав тренажерно-моделирующего комплекса (ТМК) должен быть введен программный модуль, обеспечивающий моделирование человека [1].
Движения аватаров в виртуальном пространстве ТМК предлагается разделять на локальные и глобальные. Локальные движения выполняются руками при неподвижном туловище аватара; они необходимы для взаимодействия аватара с объектами виртуального мира. Область вблизи аватара, до любой точки которой он может дотянуться рукой без перемещения своего тела, назовем зоной оперативного пространства. Таким образом, локальные движения – это движения в области оперативного пространства, а глобальные – перемещения аватара в виртуальном мире, совершаемые для попадания целевой точки в зону оперативного пространства. Глобальные движения представляют собой перемещения аватара в виртуальном пространстве ТМК на сравнительно большие расстояния. Данные движения можно представить как типовые, поскольку их набор ограничен и они, как правило, являются периодическими. Дви- жения в области оперативного пространства чрезвычайно разнообразны, их нельзя привести к типовым, так как они в полной мере определяются моделируемой ситуацией. Ввиду широчайшего многообразия движений в области оперативного пространства эти движения названы уникальными.
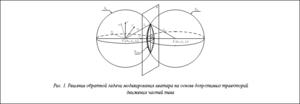 Для моделирования уникальных движений предлагается новый метод решения задачи подведения руки аватара к целевой точке с применением математического аппарата геометрии и линейной алгебры, основанный на допустимых траекториях движения частей тела аватара. Исходными данными при решении обратной задачи моделирования аватара на основе данного подхода являются положение аватара и целевой точки в виртуальном мире ТМК, параметры скелета аватара (длины звеньев, допустимые углы вращения в суставах), диапазон допустимых направлений (qц, jц) подведения руки к целевой точке, ограничивающие параллелепипеды (ОП) частей тела аватара и объектов виртуального мира, с которыми обрабатываются столкновения. В результате требуется определить обобщенные координаты qп, qпр, qз звеньев кинематической цепи руки аватара.
Для моделирования уникальных движений предлагается новый метод решения задачи подведения руки аватара к целевой точке с применением математического аппарата геометрии и линейной алгебры, основанный на допустимых траекториях движения частей тела аватара. Исходными данными при решении обратной задачи моделирования аватара на основе данного подхода являются положение аватара и целевой точки в виртуальном мире ТМК, параметры скелета аватара (длины звеньев, допустимые углы вращения в суставах), диапазон допустимых направлений (qц, jц) подведения руки к целевой точке, ограничивающие параллелепипеды (ОП) частей тела аватара и объектов виртуального мира, с которыми обрабатываются столкновения. В результате требуется определить обобщенные координаты qп, qпр, qз звеньев кинематической цепи руки аватара.
Задача определения параметров кинематической цепи руки аватара делится на три этапа.
1-й этап. Определение положения сустава запястья C3(qц, jц) в зависимости от направления подведения руки к целевой точке. Для этого вычисляется матрица МЦ,М преобразования из системы координат целевой точки в мировую систему координат [2]:
 ,
,  ,
,
 ,
,
 .
.
2-й этап. Определение допустимого множества положений локтевого сустава Спр(xпр, yпр, zпр) и применение критериев оптимизации положения локтевого сустава при действии аватара в оперативном пространстве. Для этого рассмотрим движение плеча независимо от предплечья (в отрыве от предплечья). Плечевое звено вращается в плечевом суставе, при этом локтевой сустав Спр описывает в пространстве сферу Sп с центром в Сп радиусом lп (рис. 1). Аналогично предплечье вращается независимо от плеча в суставе запястья, при этом локтевой сустав Спр описывает в пространстве сферу Sпр с центром в Сз радиусом lпр. Очевидно, что точки пересечения этих двух сфер Sп и Sпр образуют множество возможных положений локтевого сустава. Таким образом, обратная задача сводится к задаче поиска точек пересечения двух сфер, обозначенных Sп и Sпр. Для упрощения вычислений введем новую систему координат O¢x¢y¢z¢ с центром в плечевом суставе и ориентированную таким образом, чтобы сустав запястья лежал на оси O¢x¢. Тогда Sn: x2+y2+z2=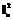 , Sпр: (x–d)2+y2+z2=
, Sпр: (x–d)2+y2+z2= .
.
Решение обратной задачи (x¢пр, y¢пр, z¢пр) представляет собой окружность радиуса Rпр= с центром в точке (xпр, 0, 0), заданную в системе координат O¢x¢y¢z¢. Окружность
с центром в точке (xпр, 0, 0), заданную в системе координат O¢x¢y¢z¢. Окружность  лежит в плоскости j, перпендикулярной оси O¢x¢ (рис. 1).
лежит в плоскости j, перпендикулярной оси O¢x¢ (рис. 1).
Вследствие того, что рука аватара обладает кинематической избыточностью, найденное решение не является единственным и представляет собой множество допустимых положений локтевого сустава, из которых путем решения оптимизационной задачи определения допустимой конфигурации скелета руки аватара выбирается наиболее соответствующее реальному движению человека.
3-й этап. Вычисление обобщенных координат qп, qпр и qз, определяющих ориентацию звеньев кинематической цепи руки аватара (плеча, предплечья и запястья соответственно) в конечной конфигурации скелета руки аватара, выполняется следующим образом.
· По найденным положениям суставов скелета руки аватара определяем направления осей Ox всех элементов скелета руки аватара. Поскольку принято, что ось Ox элемента скелета направлена вдоль элемента скелета, то оси Ox лежат на прямых, соединяющих суставы руки аватара:

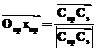 ,
, 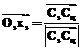 .
.
· Направления осей Oy и Oz систем координат элементов скелета руки аватара определяем таким образом, чтобы вращение ортов системы координат при движении из начальной конфигурации скелета к конечной было минимальным. Это достигается с помощью процедуры ортогонализации Грамма–Шмидта:
 ,
,
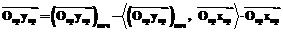 ,
,
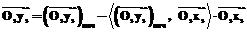 .
.
· По ортам осей систем координат строим матрицы преобразования из одной системы координат в другую для всех элементов скелета руки аватара и кватернионы, являющиеся обобщенными координатами элементов скелета.
Для выбора одного из множества найденных допустимых положений локтевого сустава при движении аватара в оперативном пространстве предлагается метод на основе решения задачи оптимизации с ограничивающими условиями, учитывающими допустимые движения элементов скелета в суставах. Переменными параметрами при оптимизации являются:
- положение локтевого сустава 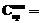 (x¢пр, y¢пр, z¢пр); поскольку координата x¢пр постоянная, а пары (y¢пр, z¢пр) лежат на окружности радиуса
(x¢пр, y¢пр, z¢пр); поскольку координата x¢пр постоянная, а пары (y¢пр, z¢пр) лежат на окружности радиуса  , возможные положения локтевого сустава описываются одной угловой координатой gÎ[0, 2p]: x¢пр=const, y¢пр=Rпрsing, z¢пр=Rпрcosg;
, возможные положения локтевого сустава описываются одной угловой координатой gÎ[0, 2p]: x¢пр=const, y¢пр=Rпрsing, z¢пр=Rпрcosg;
- направление подведения кисти к целевой точке (qц, jц): qц – отклонение кисти от нормали в целевой точке; jц – направление отклонения кисти.
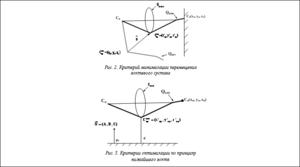
В качестве целевой функции оптимизации использована комбинация критериев минимизации перемещения локтевого сустава при движении руки аватара к целевой точке и принципа нижайшего локтя. Критерий минимизации перемещения локтевого сустава определяет такое конечное положение локтевого сустава, при котором его движение из начальной конфигурации к конечной будет минимальным (рис. 2). При этом целевая функция имеет следующий вид:
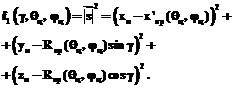
Критерий оптимизации движения руки аватара на основе принципа нижайшего локтя [3], применяемого в робототехнике, определяет такое конечное положение локтевого сустава, при котором расстояние от локтевого сустава до плоскости пола минимально (рис. 3). При этом целевая функция будет иметь вид
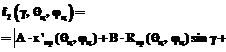
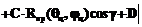 .
.
Ограничивающие условия делятся на три группы.
 1. Для учета биомеханических параметров движения руки человека применены ограничения, учитывающие максимальные углы вращения в суставах плеча, локтя и запястья. При этом необходимо для положения локтевого сустава, вычисленного на текущей итерации, для каждого i-го элемента скелета руки определить обобщенные координаты и преобразовать их в углы Эйлера
1. Для учета биомеханических параметров движения руки человека применены ограничения, учитывающие максимальные углы вращения в суставах плеча, локтя и запястья. При этом необходимо для положения локтевого сустава, вычисленного на текущей итерации, для каждого i-го элемента скелета руки определить обобщенные координаты и преобразовать их в углы Эйлера  ,
, 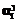 ,
,  . Тогда ограничения будут иметь вид
. Тогда ограничения будут иметь вид  ,
,  ,
, 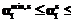
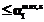 . Преобразуем их к форме, пригодной для применения в методе штрафных функций:
. Преобразуем их к форме, пригодной для применения в методе штрафных функций:



 (1)
(1)


2. Ограничения на допустимые углы подведения кисти к целевой точке  и
и 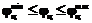 имеют следующий вид:
имеют следующий вид:
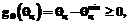
 (2)
(2)
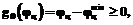
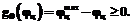 (3)
(3)
3. Ограничения, введенные для предотвращения коллизий (столкновений) элементов руки с другими частями тела аватара и с объектами виртуального мира ТМК, определяются как расстояние между ограничивающим параллелепипедом i-го элемента руки (ОПi) и ближайшим ограничивающим параллелепипедом объекта ТМК или части тела аватара (ОПobj):
 . (4)
. (4)
Таким образом, постановка задачи оптимизации положения локтевого сустава имеет следующий вид: целевая функция f(g, qц, jц)=f1(g, qц, jц)+f2(g, qц, jц)®min, ограничивающие условия (1)–(4). Функция штрафа в данном случае имеет следующий вид:  , где r – малая положительная величина [4].
, где r – малая положительная величина [4].
Экспериментальное сравнение модели движения аватара в оперативном пространстве, построенной на кинематике манипуляторов, и вышеописанной модели, основанной на допустимых траекториях движения элементов скелета руки аватара, показало, что наилучшие результаты дает модель на основе допустимых траекторий движения частей тела аватара (рис. 4).
Применение модели перемещения аватара в оперативном пространстве на основе допустимых траекторий движения позволяет практически избавиться от задержки при выводе кадров (с 25 до 23), когда выполняется расчет траектории движения руки аватара к целевой точке. При применении модели на основе теории кинематики манипуляторов проседание частоты кадров составляет более 25 % (с 25 до 18), что проявляется кратковременным зависанием изображения и его рывками (рис. 5). На данном графике также представлено сравнение разработанной модели с физическим моделированием движения на основе динамики RagDoll, применяемой в компьютерных играх, которая также проигрывает в скорости работы.
Литература
1. Ситалов Д.С. Проблемы моделирования действий оператора в современном тренажере // Программные продукты и системы. 2010. № 4. С. 137–140.
2. Цисарж В.В., Марусик Р.И. Математические методы компьютерной графики. К.: Факт, 2004. 466 с.
3. Накано Э. Введение в робототехнику; [пер. с япон.]. М.: Мир, 1988. 334 с.
4. Банди Б. Методы оптимизации. Вводный курс; [пер. с англ.]. М.: Радио и связь, 1988. 128 с.




 ,
,  ,
, ,
, .
.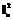 , Sпр: (x–d)2+y2+z2=
, Sпр: (x–d)2+y2+z2= .
. с центром в точке (xпр, 0, 0), заданную в системе координат O¢x¢y¢z¢. Окружность
с центром в точке (xпр, 0, 0), заданную в системе координат O¢x¢y¢z¢. Окружность  лежит в плоскости j, перпендикулярной оси O¢x¢ (рис. 1).
лежит в плоскости j, перпендикулярной оси O¢x¢ (рис. 1).
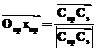 ,
, 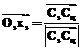 .
.
 ,
,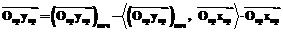 ,
,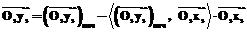 .
.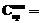 (x¢пр, y¢пр, z¢пр); поскольку координата x¢пр постоянная, а пары (y¢пр, z¢пр) лежат на окружности радиуса
(x¢пр, y¢пр, z¢пр); поскольку координата x¢пр постоянная, а пары (y¢пр, z¢пр) лежат на окружности радиуса  , возможные положения локтевого сустава описываются одной угловой координатой gÎ[0, 2p]: x¢пр=const, y¢пр=Rпрsing, z¢пр=Rпрcosg;
, возможные положения локтевого сустава описываются одной угловой координатой gÎ[0, 2p]: x¢пр=const, y¢пр=Rпрsing, z¢пр=Rпрcosg;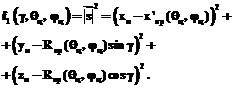
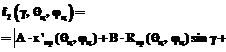
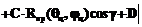 .
.
 ,
, 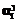 ,
,  . Тогда ограничения будут иметь вид
. Тогда ограничения будут иметь вид  ,
,  ,
, 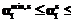
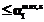 . Преобразуем их к форме, пригодной для применения в методе штрафных функций:
. Преобразуем их к форме, пригодной для применения в методе штрафных функций:


 (1)
(1)

 и
и 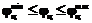 имеют следующий вид:
имеют следующий вид: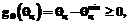
 (2)
(2)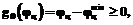
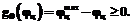 (3)
(3) . (4)
. (4) , где r – малая положительная величина [4].
, где r – малая положительная величина [4].