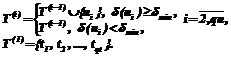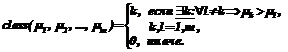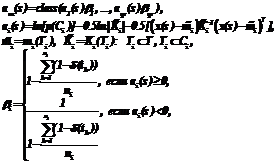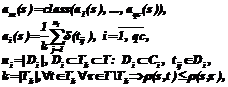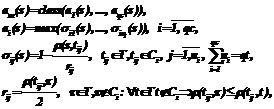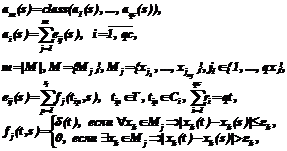Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Об одной модели корректировки имеющихся знаний на основе принимаемых решений
Аннотация:
Abstract:
| Авторы: Сикулер Д.В. (v_v_fomin@mail.ru) - Российский государственный педагогический университет им. А.И. Герцена, г. Санкт-Петербург, кандидат технических наук | |
| Количество просмотров: 9635 |
Версия для печати Выпуск в формате PDF (2.00Мб) |
Данная статья посвящена актуальнейшей проблеме, возникающей при изучении и моделировании интеллектуальной деятельности, – проблеме учета принимаемых решений и корректировки на их основе имеющихся знаний с целью повышения эффективности работы интеллектуальной системы. Частично решить указанную проблему в контексте одной из ключевых задач искусственного интеллекта позволит задача распознавания. Рассмотрим задачу распознавания группы объектов, то есть случай, когда множество распознаваемых объектов U состоит более чем из одного элемента: U={u1,…,uqu}, qu>1. Пусть эта задача решается с помощью некоторого метода распознавания M. Тогда можно предложить следующую процедуру модификации решающего правила. После распознавания каждого объекта Обозначим через dmin минимально допустимую величину коэффициента доверия, то есть порог, на основании которого распознаваемые объекты добавляются в обучающую выборку. Тогда процесс дополнения обучающей выборки представим следующим образом:
Далее введем в рассмотрение вектор доверия d (i): d (i)=d(T (i))=(d(t1),…,d(tn)), tjÎT (i), n£(qt+i–1), · байесовский классификатор для нормального распределения классов; · метод k ближайших соседей; · метод эталонов; · метод вычисления оценок. Рассмотрим, каким образом будут выглядеть модели решающих правил для перечисленных методов с учетом предложенной процедуры модификации. Предварительно введем необходимые обозначения: Ci – множество объектов, относящихся к i-му классу,
Модифицированный байесовский классификатор для нормального распределения классов. Зададим зависимость решающего правила от вектора доверия: введем корректирующий коэффициент bi для решающей функции каждого класса, то есть приведем решающую функцию к следующему виду (здесь и далее для простоты записи
где Коэффициент доверия для распознанного объекта u вычислим на основании решающих функций классов от этого объекта по следующему выражению:
Модифицированный метод k ближайших соседей. Для учета качества обучающей выборки будем вычислять решающую функцию класса ai(s) на основе коэффициентов доверия объектов этого класса, то есть приведем решающую функцию к следующей форме:
где ni – мощность множества Di объектов, относящихся к i-му классу, из множества Tk k ближайших в заданной метрике к распознаваемому объекту s элементов обучающей выборки T; r(s,t) – расстояние между объектами s и t в заданной метрике. В качестве величины коэффициента доверия распознанного объекта u используем значение максимальной из решающих функций классов, то есть Модифицированный метод эталонов. Для решающего правила метода эталонов ввиду его специфики не требуется вводить зависимость от вектора доверия. Фактически в рассматриваемом случае эта зависимость заключается в функции отбора объектов, формирующих обучающую выборку, поскольку для распознавания используются только те объекты обучающей выборки, коэффициент доверия для которых не меньше заданного порога dmin. Решающая функция имеет ту же форму, что и для немодифицированного метода, а именно:
где sij(s) – характеристическая функция, определяющая степень принадлежности и близости распознаваемого объекта s к j-му эталону i-го класса; tij – объект обучающей выборки, относящийся к i-му классу и являющийся центром j-го эталона этого класса; rij – радиус j-го эталона i-го класса, представляющий собой половину расстояния в заданной метрике до ближайшей точки отличного класса; r(s,t) – расстояние между объектами s и t в заданной метрике. В качестве величины коэффициента доверия распознанного объекта u используем значение максимальной из характеристических функций, то есть
Модифицированный метод вычисления оценок. Для учета зависимости решающего правила от вектора доверия будем вычислять функцию близости fj(t,s) между распознаваемым объектом s и элементом обучающей выборки t на основе коэффициента доверия для последнего. В этом случае решающая функция примет следующий вид:
где eij(s) – оценка распознаваемого объекта s для i-го класса по j-му опорному множеству; Mj – j-е опорное множество, включающее подмножество исходного множества признаков, по которому вычисляется степень похожести распознаваемого объекта и элемента обучающей выборки; Tij – множество объектов обучающей выборки, соответствующих i-му классу, к которым оказался близок по j-му опорному множеству распознаваемый объект; fj(t,s) – функция близости между объектами t и s, вычисляемая по j-му опорному множеству; ek – порог близости для признака xk. Коэффициент доверия для распознанного объекта u вычислим на основании решающих функций классов от этого объекта по следующей формуле:
Таким образом, рассмотренная модель может быть использована для адаптации и повышения эффективности применения существующих методов распознавания, предоставляя один из возможных путей расширения базы имеющихся знаний интеллектуальной системы. Особенностью модели является то, что она может использоваться с различными методами без существенного изменения алгоритмов, лежащих в их основе. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=290 |
Версия для печати Выпуск в формате PDF (2.00Мб) |
| Статья опубликована в выпуске журнала № 4 за 2007 год. |
Назад, к списку статей