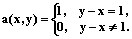Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Векторные системы усреднений на графе
Аннотация:Рассматриваются операторы усреднения функции, определенной на вершинах ориентированного графа с конеч-ным рангом вершин. Усреднение в каждой вершине происходит по смежным вершинам с весами, заданными на реб-рах графа. Исследуются требования, необходимые и достаточные для однозначного восстановления функции по ее усреднениям в форме степенного ряда. Показано, что при невыполнении этих условий строятся минимальные в оп-ределенном смысле дополнительные операторы, которые обеспечивают обратимость полученного векторного опера-тора.
Abstract:It considers the operators of function averaging which defined on vertexes of oriented graph with finite vertex number. The averaging occurred in every vertex by incident vertexes in the graph with weights determined on detected edges in graph. It researched necessary and decent condition for that operator has convertibility in form of power-mode row. If those conditions are not true then it builds the additional operators for getting convertibility vector operator, and that extension is minimal in any sing determine meaning.
| Авторы: Коганов А.В. (koganow@niisi.msk.ru) - НИИСИ РАН, г. Москва, кандидат физико-математических наук | |
| Ключевые слова: алгоритм восстановления, томография, формула обращения, ядро оператора, ориентированный граф, интегральная геометрия |
|
| Keywords: restore algorithm, , inversion formula, operator kernel, oriented graph, integral geometry |
|
| Количество просмотров: 12400 |
Версия для печати Выпуск в формате PDF (5.83Мб) Скачать обложку в формате PDF (1.28Мб) |
Во многих задачах томографии, рентгеноскопии и математического моделирования необходимо получить объемное или плоское изображение объекта по данным об интенсивности излучения, которое усреднено по некоторой системе пространственных областей или сечений. Это клас-сическая задача интегральной геометрии, относящаяся к функциональному анализу и его вычислительным приложениям (например, [1, 2]). В современных исследованиях исходное пространство, на котором восстанавливается распределение интенсивности, часто изначально имеет структуру дискретного графа, а исходная информация относится к весовым усреднениям по подграфам. Исследованию методов восстановления функции в таких ситуациях посвящены работы [3–5]. В данной работе рассматривается задача получения необходимой дополнительной информации в тех случаях, когда исходная информация недостаточна для ее однозначного решения. При этом предполагается, что дополнительная информация тоже будет получена в форме усреднений функции по подмножествам. Устанавливаются минимальные требования к таким данным. Классическая проблематика интегральной геометрии связана с обращением операторов, усредняющих функцию, определенную на линейном пространстве с мерой, по заданной системе прямых или к-плоскостей в этом пространстве. В последние годы стала развиваться теория обращения операторов усреднения на пространствах с комбинаторной структурой, содержащих конечное или счетное число точек [3, 4]. В [5] показана связь комбинаторных и аналитических методов. При этом возникают новые формулы обращения на непрерывных пространствах с мерой. В данной статье рассматривается конструкция нескольких усреднений для функций, определенных на комбинаторном пространстве. Определения систем усреднения и соответствующей алгебры операторов Определение 1. Скалярной системой усреднений áX, Y, F, añ на счетном множестве X с заданным линейным пространством функций F вида f: X®
Множество X назовем базовым, множество Y – параметрическим, значения a(x, y) – весами усреднения для точки x с параметром y. Скалярная система усреднений обратима, если по образу функции haf(×) можно восстановить исходную функцию f (отображение ha инъективное). Векторной системой усреднения назовем конечный, или счетный, набор систем усреднений áX, Y, F, aiñ, i=1, …, m, с общими базовыми и параметрическими множествами. Векторная система усреднений обратима, если по образу функции
можно восстановить исходную функцию f (отображение h(a) инъективное). В тех случаях, когда утверждение относится к обоим типам систем усреднения, будем говорить о системе усреднения без уточняющих слов. Определение 2. Скалярная система усреднения на графе определяется следующим. I. Базовое множество совпадает с параметрическим множеством X=Y. II. Для каждого yÎX множество тех xÎX, для которых a(y, x)¹0, конечно:
Это свойство назовем прямой финитностью усреднения: для каждого значения параметра усреднение ведется по конечному числу точек. III. Для каждого xÎX множество тех yÎX, для которых a(y, x)¹0, конечно:
Это свойство назовем обратной финитностью усреднения: каждая точка участвует в усреднении для конечного числа значений параметра. Наличие прямой и обратной финитности назовем двусторонней финитностью. Такая система отображается на граф с множеством вершин X и ребрами (y, x), на которых a(y, x)¹0. По условию III в каждую вершину этого графа входит конечное число ребер, а по условию II из каждой вершины выходит конечное число ребер. Сами значения a(y, x) можно рассматривать как веса соответствующих ребер. Векторная система усреднения на графе определяется тем, что каждая из скалярных компонент является системой усреднения на графе. В этом случае граф имеет ребро (y, x), если есть ненулевой вес ai(y, x)¹0 для некоторой компоненты iÎ{1, …, m}. В системе усреднения на графе можно говорить о системе весов на ребрах. Этот граф назовем соответственным системе усреднения. Стандартным пространством функций для систем усреднений на графе определим пространство F всех финитных функций, принимающих ненулевые значения в конечном числе точек. Это множество точек назовем носителем функции. Областью определения всех функций считаем все базовое множество X. На этих функциях значение оператора усреднения всегда определено и также финитно. Поэтому определена итерация любых двух операторов из векторной системы усреднения. Тогда эти операторы образуют алгебру по умножению (итерация операторов) и сложению (сумма образов) с обычным умножением на число (умножение образа). Для векторной системы усреднения это алгебра с m образующими, которая в общем случае некоммутативна. Эту алгебру назовем соответственной системе усреднения. Ее образующие – операторы Определение 3. Вычислим кратные веса для скалярной системы усреднения
Тогда
Лемма 1. Для скалярной системы усреднения на графе верна формула
Доказательство по индукции непосредственно из (1) и (4). Определение 4. Вычислим кратные веса для векторной системы усреднения
Тогда
Лемма 2. Для векторной системы усреднения на графе верна формула
Доказательство по индукции непосредственно из (1) и (7). Если все индексы принимают одно значение, то формула (8) совпадает с (5). Поэтому лемма 2 является обобщением леммы 1 на случай нескольких образующих соответственной алгебры. Определение 5. Цепью длины n–1 на базовом множестве системы усреднения назовем конечную последовательность элементов x1, …, xn, в которой соседние члены различны xi¹xi+1 и связаны ребром в соответственном графе. В скалярном случае a(xi, xi+1)¹0, i=1, …, n–1. Для векторной системы усреднения наличие ребра означает наличие для каждой пары соседних членов хотя бы одной системы aj(i), j(i)Î{1, …, m}, в которой выполнено условие aj(i)(xi, xi+1)¹0. Цепь в векторной системе усреднения называется строгой, если в ней для всех i=1, …, n–1 дополнительно выполнено условие aj(i)(xi, xi)¹0. Определение 6. Векторная система усреднения называется ациклической, если в ней все цепи не содержат повторяющихся членов. Это означает, что из условия a(x, y½i1, …, it)¹0 для некоторой последовательности i1, …, it при y¹x следует, что для любой последовательности i¢1, …, i¢t¢ выполнено равенство a(y, x½i¢1, …, i¢t)=0 (если есть путь из одной точки в другую, то нет обратного пути). В частности, для скалярной ациклической системы усреднений из условий y¹x и a(x, y½t)¹0 для некоторого значения t³1 следует, что для любого значения t¢³1 выполнено условие a(y, x½t¢)=0. Соответственные графы ациклических систем не имеют циклов при движении по направлению ребер, но могут иметь петлю в некоторой вершине, если a(x, x)¹0 или ai(x, x)¹0 для некоторой компоненты iÎ{1, …, m}. Такую точку xÎX базового пространства (то есть вершину соответственного графа) в ациклической векторной системе усреднения назовем петлевой. Задача пополнения векторной системы усреднения Данная задача возникает, когда имеется необратимая система усреднения. Она заключается в добавлении к этой системе еще одного или нескольких скалярных операторов усреднения так, чтобы новая векторная система стала обратимой. Замечание 1. Системе усреднения соответствует линейный оператор h(a). Поэтому необратимость означает, что ядро этого оператора нетривиально: dim ker(h(a))³1. Если же ядро тривиально, ker(h(a))={0}, то оператор обратим. В случае конечного базового множества #X<¥ задача обращения сводится, например, к построению матрицы обратного оператора Если ядро нетривиально, функции из ядра по определению отображаются в ноль всеми компонентами оператора системы усреднения
теорема 1. ядро оператора векторной системы усреднения совпадает с пересечением ядер компонент: Это следует из формулы (9). Утверждение 1. Задача пополнения векторной системы усреднения решается любым (и только таким) набором скалярных систем
Это утверждение следует из теоремы 1 и замечания 1. Если обозначить расширенную систему усреднения a¢=(a1, …, am, am+1, …, am+k), то левая часть формулы (11) определяет ядро ker(h(a¢)). Пояснение. Решение задачи пополнения принципиально неоднозначно. Очевидно, возможным решением является добавление любой обратимой системы усреднения. Тогда можно отбросить всю исходную систему. Ограничения, которые возникают при введении новых операторов усреднения, обычно задаются прикладными условиями и не могут быть определены математически заранее. Поэтому удобно иметь общее описание всех возможных пополнений и потом искать решение в заданных дополнительных ограничениях. Одно из таких описаний дает утверждение 1. Определение 7. Назовем пополнение необратимой системы усреднения минимальным, если ядро этого пополнения линейно дополнительно к ядру исходной системы, то есть все пространство функций является прямой суммой ядер исходной и пополняющей систем усреднения. Очевидно, в этом случае ядро пополненной системы усреднения тривиально.
Определение 8. назовем приведенной системой любую минимальную по составу скалярных операторов подсистему системы усреднения, ядро которой совпадает с ядром всей системы. Пояснение. Если у системы усреднения нетривиальное ядро, функцию можно восстановить только с точностью до псевдообращения усреднения. У систем с одинаковыми ядрами одинаковая погрешность оператора псевдообращения (теряется ортогональная проекция исходной функции на ядро как на подпространство). В частности, если система обратима, то и приведенная система об- ратима. Таким образом, переход к приведенной системе усреднения уменьшает (в общем случае) размерность векторного усреднения без потери полезной информации о функции. термин «минимальное пополнение» в определении 7 оправдан тем, что в силу свойства (12) из приведенной исходной системы нельзя отбросить ни одного скалярного оператора без потери обратимости пополненной системы. Утверждение 2. если исходная система и минимальное пополнение приведенные, полученная пополненная система остается приведенной. Это следует из свойства (12), поскольку отбрасывание любой скалярной компоненты усреднения приведет к увеличению одного из двух прямых слагаемых и тогда возникнет нетривиальное пересечение ядер в левой части формулы (11). Утверждение 3. Если исходная система была усреднением на графе и пополнение является усреднением на графе, это свойство сохраняет пополненная система. Это проверяется непосредственно по условиям I–III определения 2 с учетом того, что объединение конечного числа конечных множеств будет конечным. Метод построения минимального пополнения для систем усреднения на графе. Рассмотрим произвольную функцию В силу прямой финитности можно записать
Определим
Обозначим Dy носитель функции y, который конечен, поскольку оператор усреднения определен на пространстве финитных функций. Введем скалярное произведение функций f, f¢ÎF: Введем новые веса усреднения:
С функцией y свяжем усредняющий оператор hb, действующий на F. По определению ядра
Поскольку функция y финитная, то оператор (16) двусторонне финитный (в усреднении участвуют только точки из носителя функции y и только для точек x из этого носителя). Для функций, ортогональных ядру оператора h(a) в смысле скалярного произведения (15), значение f*y обнуляется. Обозначим y(a) некоторый базис ядра оператора h(a). Рассмотрим векторный оператор
Теорема 2. Оператор (17) является приведенным минимальным пополнением системы усреднения h(a). Доказательство.
Таким образом, оператор (17) является минимальным пополнением. Покажем, что система усреднения h(b½y) является приведенной. Устраним из этой системы любую функцию yÎY. Введем обозначения. Пусть S – некоторый набор функций из F. Тогда áSñ – линейная оболочка этих функций; ortáSñ – ортогональное дополнение к áSñ; Pr(f)áSñ – проекция функции f на áSñ. В этих обозначениях из (18)
Следствие. Из теоремы 2 и утверждения 3 следует: если ядро системы усреднения на графе конечномерное, возможно приведенное пополнение до обратимой системы на графе. Пополнение ациклических систем усреднения на графе Рассмотрим ациклическую систему усреднения h(a) на графе (АСУГ – определение 6). Теорема 3. Если в АСУГ все вершины петлевые, она обратима. Доказательство. Введем функцию перехода i(x), удовлетворяющую условию a(x, x½i(x))¹0. По условию теоремы эта функция может быть задана в каждой точке. В условиях теоремы для каждой вершины верна формула Для усреднения функции по строгим цепям требуются модифицированные кратные веса усреднения. Суммарные относительные веса перехода из точки x в точку y по строгим цепям длины t=1,… с использованием функции перехода i(×) можно вычислить по рекуррентным формулам относительно параметра t:
Многократная итерация формулы (19) позволяет записать бесконечный формальный ряд:
Поскольку функция финитная и система на графе, каждая сумма содержит конечное число ненулевых членов. А поскольку система ациклическая, точки на строгих цепях не повторяются и, начиная с некоторого значения параметра t, суммы содержат только нулевые значения функции. Поэтому для каждой функции из области определения оператора усреднения ряд (21) содержит только конечное число ненулевых членов и, следовательно, сходится. Это доказывает теорему. Теорема 4. Для пополнения векторной АСУГ достаточно добавить скалярную или векторную систему усреднения, которая имеет петли во всех тех точках, где исходная система не имела петель. (В других отношениях добавленная система может быть произвольной.) Это сразу следует из теоремы 3. Замечание 2. Указанное в теореме 4 пополнение в общем случае не будет ни минимальным, ни приведенным. Но, если в пополненной системе устранение любой компоненты приводит к исчезновению петли в некоторой точке, можно говорить об условно неприводимой системе. В этом случае все компоненты необходимы для применения формулы обращения (21). Замечание 3. Наличие в АСУГ непетлевых точек делает невозможным обращение усреднения по формуле (21), но при этом может существовать обратимость иными методами. Теорема 3 утверждает только достаточные, но не необходимые условия обратимости АСУГ. Рассмотрим, например, скалярную АСУГ на двусторонне бесконечном линейном соответственном графе с вершинами {…; –1; 0; +1} и ребрами вида (i, i+1). Веса усреднения заданы формулой
Тогда система не имеет ни одной петли. Оператор усреднения задан формулой h(a)f(x)=f(x+1). Это усреднение очевидно обратимое: f(x)= =h(a)f(x–1). Таким образом, теорема 3 действительно не дает необходимых условий обратимос- ти АСУГ. Алгебра, порожденная векторным усреднением на графе Компонента векторного усреднения на графе является оператором, сохраняющим финитность функции. Поэтому на пространстве финитных функций определена алгебра, порожденная компонентами векторного усреднения с операциями суммы и умножения. Сумма операторов определена как сумма образов функции операнда, а произведение – как последовательное применение операторов. Данное произведение в общем случае некоммутативно. Назовем эту алгебру соответственной системе усреднения. Заметим, что любое произведение конечного числа операторов компонент (включая и степени одного оператора) дает снова оператор на графе. Соответственный граф получается объединением в одно ребро нескольких последовательных ребер графа, соответственного исходной системе усреднения. Поэтому данная некоммутативная алгебра позволяет получать новые операторы усреднения в форме полиномов от исходных компонент усреднения. При этом добавление нескольких полиномов в качестве новых компонент усреднения увеличивает размерность образа функции и число ребер соответственного графа, но не меняет соответственную алгебру. Новые операторы в общем случае линейно не зависят от исходных компонент, но по определению входят в порожденную ими алгебру. Если исходная система на графе была ациклической, любое ее расширение полиномами в соответственной алгебре сохраняет ацикличность. Это следует из принципа преобразования соответственного графа. Если в исходном графе не было циклов длиннее единицы, последовательное соединение ребер этого графа не породит цикла. В частности, если вершина исходного соответственного графа была непетлевой, и в новом графе она останется непетлевой. Таким образом, полиноми- альное расширение АСУГ не может дать пополнения этой системы до обратимой по формуле (21). Подводя итоги, отметим, что в работе введено понятие векторной системы усреднения на графе. Для ациклических графов построена алгебра таких операторов, определенных на финитных функциях. Эта алгебра в общем случае имеет некоммутативное умножение. Найдены необходимые и достаточные условия обратимости таких операторов на ациклических графах, если обращение строится в форме ряда от степеней оператора. Введены понятие приведенной системы усреднения, позволяющее упростить исходную систему без потери информации о преобразуемой функции, а также понятие минимального расширения системы усреднения, позволяющее ввести наименьшее дополнительное число операторов усреднения в необратимую систему для обеспечения обратимости расширенной системы. Разработан метод построения таких дополнительных систем. Таким образом, решена задача получения минимально необходимой дополнительной информации в форме значений новых операторов усреднения на заданном графе, которая позволяет восстановить функцию после ее усреднения в исходной системе методом разложения полученного векторного усреднения в степенные ряды. Литература 1. Гельфанд И.М., Гиндикин С.Г., Граев М.И. Избранные задачи интегральной геометрии. М.: Добросвет, 2000. 208 с. 2. Гельфанд И.М., Граев М.И., Виленкин Н.Я. Обобщенные функции / Интегральная геометрия и связанные проблемы теории представлений. М.: Физматгиз, 1962. Т. 5. 3. Коганов А.В. Комбинаторные методы интегральной геометрии: в сб. Математика. Компьютер. Образование. Вып. 12. Ч. 2. М.–Ижевск: НИЦ «Регулярная и хаотическая динамика». 2005. С. 746–758. 4. Граев М.И., Коганов А.В. Алгоритмы восстановления функции через ее усреднения по подмножествам // Програм- мные продукты и системы. 2008. № 4. С. 33–38. 5. Коганов А.В. Интегральная геометрия на системах покрытий // Математические исследования: сб. тр.; [под ред. акад. В.Б. Бетелина]. М.: НИИСИ РАН, 2005. С. 197–230. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2900 |
Версия для печати Выпуск в формате PDF (5.83Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2011 год. [ на стр. 3 – 7 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 и с параметром усреднения из счетного множества Y назовем заданный набор функций a(y, x):X®
и с параметром усреднения из счетного множества Y назовем заданный набор функций a(y, x):X®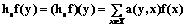 . (1)
. (1)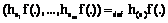 (2)
(2)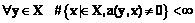 .
. .
.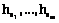 .
.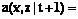
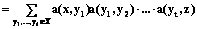 ; (3)
; (3)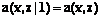 .
.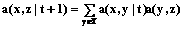 . (4)
. (4)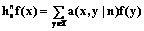 . (5)
. (5)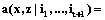
 ; (6)
; (6) .
.
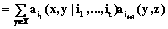 . (7)
. (7) . (8)
. (8)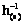 .
.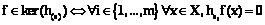 . (9)
. (9)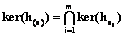 . (10)
. (10)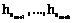 , у которых пересечение ядер имеет тривиальное пересечение с ядром исходной системы:
, у которых пересечение ядер имеет тривиальное пересечение с ядром исходной системы: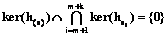 . (11)
. (11)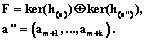 (12)
(12)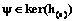 . Обозначим
. Обозначим  .
.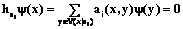 , (13)
, (13)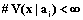 ; i=1, …, m; xÎX.
; i=1, …, m; xÎX. , тогда #V(x)<¥ и
, тогда #V(x)<¥ и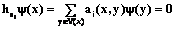 ; i=1, …, m. (14)
; i=1, …, m. (14) . (15)
. (15)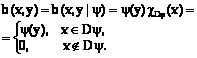
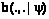 можно записать
можно записать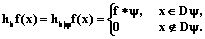 (16)
(16)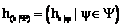 . (17)
. (17)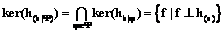 ,
,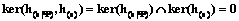 , (18)
, (18) .
.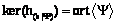 . Обозначим Y¢=Y\{y}. Поскольку Y является базисом ядра, то
. Обозначим Y¢=Y\{y}. Поскольку Y является базисом ядра, то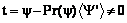 ;
;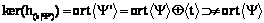 . Теорема доказана.
. Теорема доказана.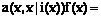
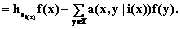 (19)
(19)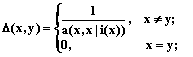
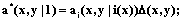
 . (20)
. (20)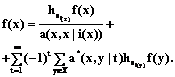 (21)
(21)