Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритмы навигации на внешней поверхности модели международной космической станции
Аннотация:Передвижения по внешней поверхности международной космической станции космонавт осуществляет, держась за специальные поручни. Поскольку станция имеет большие размеры, для эффективного и безопасного перемещения необходимо решать задачу навигации, то есть строить оптимальный маршрут между начальным и целевым поручнями. В данной статье предлагаются алгоритмы поиска маршрутов по критерию минимальной длины или наименьшей сложности пути между двумя заданными поручнями. Рассматриваются случаи нахождения как одного, так и всех возможных маршрутов, отвечающих выбранному критерию. Поиск маршрутов осуществляется с помощью графа, в котором вершины соответствуют поручням на станции, а ребра показывают возможность перехода между соседними поручнями. Для решения задачи строится ориентированный подграф, в котором любой путь между начальной и целевой вершинами маршрута является кратчайшим (или имеет наименьшую сложность прохождения) в исходном графе. Предложенные алгоритмы можно использовать при реализации систем навигации для имитационно-тренажерных комплексов подготовки космонавтов. Применение таких систем в тренажерных комплексах позволит повысить эффективность обучения на них специалистов для выполнения работ на внешней поверхности станции. В статье проиллюстрирована система навигации в видеотренажерном комплексе, основанная на использовании описанных алгоритмов. Для отображения пути, построенного между двумя поручнями, осуществляется подсветка входящих в него поручней заданным цветом. Кроме того, затрагивается вопрос о перспективах развития тренажерных комплексов в направлении создания такой системы, которая одновременно использует технологии виртуальной реальности (шлемы виртуальной реальности, компьютерные перчатки) и систему навигации.
Abstract:Spaceman moves along ISS outer surface with help of special rails. Station is large, and in order to provide effective and safe movement it is necessary to solve navigation problem, e.g. designing the best route between start and target rails. This article offers route search algorithms according to criteria of minimum length and complexity between two given rails. The article reviews calculation of one or all possible routes that meet selected criteria. Search of a route is made with flow chart, which presents rails in the form of peak and ribs reflect the ways of passing between two neighbored rails. The solution involves oriented sub flow chart, where any route between start and final peaks presents the shortest one (or the least difficulty to pass it) in initial chart. Such algorithms can be used in implementation of navigation systems for simulation training facilities provided for spacemen. Use of such systems in the training facilities increases training effectiveness for those who work outside of station. This article illustrates navigation system in video training facility based on mentioned algorithms. The constructed route between two rails shall be highlighted with specified color. In addition, the article discusses issue related to the future of training facilities concerning development of system that can use virtual reality technology (virtual reality helmet, computer gloves) and navigation system. (The work is supported by RFBR, grant No 10-07-00317).
| Авторы: Мальцев А.В. (avmaltcev@mail.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, кандидат физико-математических наук, Михайлюк М.В. (mix@niisi.ras.ru) - НИИСИ РАН, г. Москва, Москва, Россия, доктор физико-математических наук | |
| Ключевые слова: видеотренажеры., высокореалистичные модели, путь, граф, навигация, виртуальная реальность |
|
| Keywords: video trainers, high realistic models, path, graph, navigation, virtual reality |
|
| Количество просмотров: 9777 |
Версия для печати Выпуск в формате PDF (7.64Мб) Скачать обложку в формате PDF (1.33Мб) |
Одним из важнейших инструментов для изучения космоса является международная космическая станция (МКС), позволяющая проводить научные и технические эксперименты в различных областях знаний. Подготовка специалистов для работы на МКС осуществляется с помощью специальных имитационно-тренажерных комплексов и систем, основанных на использовании технологий виртуальной реальности. В таких комплексах и системах реальная обстановка (как внутри, так и вне станции) заменяется на визуализируемую в масштабе реального времени трехмерную виртуальную сцену. Модель МКС содержит более 1 млн полигонов и более 358 МБ текстур (включая текстуры рельефа, отражения и прозрачности). При ее визуализации с помощью системы GLView [1] моделируются источники освещения типа «фара», а также мягкие и жесткие тени. Модель Земли содержит более 150 тысяч полигонов и более 1 ГБ текстур. Одной из актуальных и важных задач, возникающих при обучении космонавтов, является формирование навыков ориентации на внешней поверхности МКС. В настоящее время станция насчитывает несколько десятков модулей и имеет протяженность более ста метров. Передвигаясь по ней, космонавт может заблудиться или выбрать неэффективный маршрут, поэтому навыки ориентации очень важны для его плодотворной и безопасной работы. В целях безопасности при перемещении по внешней стороне станции от одного объекта к другому космонавт должен держаться за специальные поручни (и прикрепляться к ним с помощью карабинов), которые закреплены на поверхности космических модулей. Для эффективного передвижения от начального положения к нужному объекту желательно знать кратчайший маршрут, то есть маршрут, содержащий наименьшее количество поручней. Прежде чем выйти в открытый космос и проводить работы в удаленных частях станции, космонавт должен выработать маршрут передвижения по поручням от его начального положения (например выходного люка) до места назначения (места проведения необходимых работ). Этот маршрут он может выделить на виртуальной модели МКС, отмечая вручную поручни на пути с помощью указателя или используя автоматические алгоритмы. В данной статье предлагаются алгоритмы поиска маршрутов между двумя заданными поручнями, исходя из минимальной длины или наименьшей сложности пути, позволяющие реализовать навигационную систему в космическом видеотренажере. Поиск кратчайшего маршрута Под длиной маршрута будем понимать число поручней на его протяжении. Кратчайший маршрут между двумя выбранными поручнями – это любой маршрут между ними, имеющий минимальную длину. Для его определения предлагается использовать неориентированный граф G, вершины которого соответствуют объектам типа «поручень» в виртуальной модели станции, применяемой в имитационно-тренажерных комплексах подготовки космонавтов [2]. При этом любые две вершины A и B графа связаны ребром, если космонавт может непосредственно переместиться с поручня A на поручень B. Основой предлагаемого алгоритма нахождения какого-либо (одного) кратчайшего маршрута в графе G от начальной вершины VH до целевой вершины VK (а значит, и кратчайшего маршрута между соответствующими поручнями на поверхности станции) является остовное дерево G' графа G с корнем в VK (то есть дерево, которое содержит все вершины графа G) [3, 4]. Заметим, что корнем G' является конечная вершина VK пути (а не начальная вершина VH), так как это облегчает построение пути из VН в VК. Построим некоторое поддерево G'' остовного дерева G', содержащее вершины VK и VH. При построении и сохранении дерева G'' в памяти компьютера используем структуру данных уже имеющегося графа G, дополнив ее необходимой информацией. Для этого к каждой вершине G добавим указатель P на ее родительскую вершину в дереве G''. После того как остовное поддерево G'' найдено, в нем в вершине VH будет записана ссылка на родителя этой вершины, в этом родителе – ссылка на его родителя и так далее до вершины VK. Поэтому остается только пройти по всем этим ссылкам от вершины VH до VK и записать индексы посещенных вершин. Эти вершины и будут входить в искомый кратчайший маршрут от VH до VK. Для хранения графа G используем файл со следующей структурой: n S0, i0, j0,0 , …, j0,m … Sn-1, in-1, jn-1,0 , …, jn-1, q Первая строка содержит общее количество n вершин графа G. Каждая следующая строка включает последовательно символьное имя Sk (k Для работы с графом используем структуру данных, находящуюся в оперативной памяти и представляющую собой массив вершин, каждая из которых содержит – имя S соответствующего вершине поручня в сцене; – список J вершин, связанных ребром с данной вершиной в графе G; – флаг F посещения; – ссылку P на родительскую вершину (необходимую для построения G''). В начале работы флаг посещения и ссылку на родительскую вершину устанавливаем равными 0. Рассмотрим нахождение кратчайшего маршрута между вершинами VH и VK графа G. Пусть F(V) – флаг посещения вершины V, а J(V) и P(V) – список связанных с ней вершин и ссылка на родителя соответственно. Тогда получаем следующий алгоритм Tree(G, VH, VK) поиска кратчайшего маршрута между вершинами VH и VK в графе G. Начало. 1. Организация пустой очереди Q вершин; 2. Добавление VK в Q и установка F(VK) в 1; 3. Цикл, пока Q не пуста или не найдена вершина VH: Выборка вершины V из Q; Цикл по вершинам Vk Если F(Vk)=0, то: P(Vk)=V; Если Vk=VH , то выход из цикла; F(Vk)=1; Добавление Vk в Q; Конец цикла Конец цикла 4. Проход по ссылкам P от VH до VK с записью в память индексов вершин, входящих в маршрут. Конец.
После выполнения шагов 1–3 алгоритма мы получаем в памяти дерево кратчайших путей G'', представленное на рисунке 2. Поскольку вершина V5 находится на более глубоком уровне дерева G'' от корня V1, чем искомая вершина V6, построение G'' прекращается до ее обработки. Следовательно, V5 не входит в G''. Проходя по ссылкам P(V6), P(V3), P(V2) и записывая индексы посещенных вершин, получаем кратчайший маршрут из V6 в V1: V6àV3àV2àV1. Видно, что полученный маршрут совпадает с одним из двух имеющихся путей, содержащих минимальное число ребер. Выбор конкретного кратчайшего маршрута из нескольких возможных вариантов обусловлен порядком обработки вершин при построении остовного поддерева. В рассмотренном примере из двух вершин одного уровня глубины от корня приоритет в порядке обработки отдавался вершине с меньшим индексом. Поиск всех кратчайших маршрутов Во многих случаях необходимо не просто знать один кратчайший маршрут между двумя поручнями, а иметь выбор из различных вариантов. Для этого желательно иметь представление обо всех возможных кратчайших маршрутах между двумя вершинами графа. Использование алгоритма, предложенного ранее, не может обеспечить решение данной задачи. Однако некоторая его модификация позволит выполнить поиск всех кратчайших путей между двумя вершинами графа G, а значит, и между соответствующими поручнями на поверхности станции. Суть такой модификации алгоритма заключается в том, что вместо остовного дерева G' с корнем в VK будет построен ориентированный подграф G1, в котором любой путь от VH до VK кратчайший между теми же вершинами в графе G. Фактически в G1 для каждой пары вершин все пути между ними будут иметь одинаковую длину. Формирование структуры G1 необходимо начинать с вершины VK. Пусть L(V) – уровень вершины V в графе G1, равный количеству ребер на пути от V до VK. Для каждой вершины V≠VK следует сохранять ссылки на всех родителей VP,i в графе G1, для которых L(VP,i)=L(V)–1, то есть уровень родителя на единицу меньше уровня V. С целью оптимизации достаточно ограничиться построением подграфа G1', содержащего вершины с уровнями до L(VH) включительно. Построив G1', необходимо выполнить рекурсивную функцию, проходящую по всем путям от VH до VK в G1' и записывающую в память индексы вершин, входящих в эти пути. Для реализации описанной модификации алгоритма поиска кратчайших путей определим структуру информации о каждой вершине следующим образом: – имя S соответствующего вершине поручня в сцене; – список J вершин, связанных ребром с данной вершиной в графе G; – флаг F посещения; – уровень L вершины; – массив ссылок P на родительские вершины.
Начало. 1. Организация пустой очереди Q вершин; 2. Добавление VK в Q; 3. F(VK)=1, L(VK)=0, LS=1 000 000; 4. Цикл, пока Q не пуста: Выборка вершины V из Q; Если L(V)=LS, то выход из цикла; Цикл по вершинам Vk Если F(Vk)=0, то: // Vk – новая вершина F(Vk)=1; // запись номера уровня L(Vk)=L(V)+1; Добавление Vk в Q; Если L(Vk)>L(V), то: // V – родитель Vk в G1' Добавление V в P(Vk); Если Vk=VH , то: // найдена нужная вершина LS=L(VH); Конец цикла Конец цикла 5. k=1, добавление индекса VH в M[1]; // k – глобальная переменная 6. Запуск рекурсивной функции поиска путей f(VH); Конец. Рекурсивная функция f(V) выполняет запись в память всех кратчайших путей от вершины V до вершины VK и имеет следующий алгоритм: fR(V) { Если (V≠VK), то: l=k; n=size(M[k]); Цикл по i от 1 до size(P(V)) Если i>1, то: k=k+1; Копирование n первых элементов из M[l] в M[k]; Добавление индекса вершины P(V)[i] в конец M[k]; f (P(V)[i]); Конец цикла } По завершении шага 6 алгоритма поиска всех кратчайших путей получаем k кратчайших путей из VH в VK, сохраненных в массиве M. В каждой строке массива M будет содержаться перечень вершин одного из кратчайших путей, начиная с VH и заканчивая VK. Проиллюстрируем работу предложенного алгоритма с помощью графа G, изображенного на рисунке 1. После выполнения шагов 1–4 получаем в памяти граф G1', представленный на рисунке 3. Поскольку L(V5)>L(V6), построение G1' прекращается до обработки вершины V5. Следовательно, она не входит в G1'. После шага 6 получаем два кратчайших маршрута из V6 в V1: V6àV3àV2àV1 и V6àV7àV2àV1. В данном случае массив M будет состоять из двух элементов (путей), длина каждого – 4 вершины. Поиск маршрута минимальной сложности Выбор маршрута между двумя поручнями может быть обусловлен не только его длиной (количеством поручней), но и сложностью прохождения. Например, если при прохождении проложенного маршрута существует вероятность повреждения оборудования, размещенного на поверхности станции, или в него входит труднопроходимый участок, имеет смысл выбрать более длинный, но менее сложный путь. В этом случае для нахождения оптимального пути необходимо использовать взвешенный граф G [4]. В нем каждое ребро будет иметь вес, равный числовой оценке перемещения между поручнями на станции, соответствующими вершинам этого ребра. Определить путь из VH в VK, имеющий минимальную сложность, можно с помощью алгоритма Дейкстры [4, 5]. Основная идея алгоритма Дейкстры состоит в последовательном (пошаговом) уточнении минимального расстояния (веса) между вершиной VН и всеми ближайшими вершинами до тех пор, пока не встретится вершина VК. При этом в каждой обработанной вершине записывается родитель, то есть предыдущая вершина по найденному до сих пор минимальному по сложности пути. Вначале вершина VН помечается и ей присваивается вес 0, а всем остальным – очень большой (бесконечный) вес. На каждом шаге выбирается неотмеченная вершина V с минимальным весом и рассматриваются все ее неотмеченные соседи Vj. Если вес соседа Vj больше суммы веса выбранной вершины V и веса ребра от нее к Vj, то вес Vj заменяется этой суммой, а родитель заменяется на V. После рассмотрения всех соседей выбранная вершина V помечается. Процесс заканчивается тогда, когда на очередном шаге выбирается вершина VК. В результате получается некоторый подграф G2. Для реализации алгоритма определим массив S структур, каждый i-й элемент которого соответствует вершине Vi и содержит следующую информацию: вес di вершины, флаг-отметка Fi (0 – в процессе обработки, 1 – обработка завершена) и указатель Рi на родителя. Первоначально все веса di равны бесконечности (очень большому числу), все флаги Fi=0 и все Рi пустые. Для заданных VН и VК обозначим через kН и kК их индексы в массиве S, через u(Vk, Vj) – вес ребра (Vk, Vj), а через I(V) – множество индексов вершин, соседних с V. Тогда алгоритм Дейкстры поиска кратчайшего пути между вершинами VН и VК во взвешенном графе G Dijkstra(G, VH, VK) можно записать следующим образом. Начало. 1. k=kК, dk=0; 2. Цикл Цикл по jÎI(Vk) Если Fk=0 и dj>dk+u(Vk, Vj), то: // Vk – неотмеченная вершина, Vj – сосед Vk dj=dk+u(Vk, Vj); // в Vj записывается ссылка на // предыдущую вершину Vk минимального пути Pj=Vk; Конец цикла // помечаем вершину как обработанную Fk=1;
Приравниваем k индексу этой вершины, то есть k=t; Если k=kН, то выход из цикла; Конец цикла 3. Проход по ссылкам Pj от Конец. Рассмотрим в качестве примера тот же граф G, что и ранее, но с весами на ребрах (см. рис. 4). В отличие от графа на рисунке 2 алгоритм Дейкстры строит кратчайший путь (V6àV5àV4àV3àV2à àV1), включающий 5 ребер, но имеющий вес 11. Существует также и другой путь того же веса, а именно (V6àV7àV2àV1), включающий 3 ребра. Интересно, что если применить алгоритм Дейкстры от начальной вершины V1 до конечной V6, то получится именно этот путь. Таким образом, для алгоритма Дейкстры существенно, откуда начинать. В связи с тем, что между выбранными вершинами может быть несколько путей одинаковой сложности (веса), возникает задача их нахождения. Для решения этой задачи можно реализовать алгоритм GenDijkstra(G, VH, VK), использующий ту же идею, что описана выше, а именно: в каждой вершине нужно записывать ссылку не на одного родителя, а на нескольких, то есть как бы список родителей. Каждый из них будет являться одной из предыдущих вершин одного из путей минимального веса (построенного до данного момента). С помощью рекурсивной функции f(VH), описанной ранее, можно выписать все пути минимального веса из VН в VК. Как уже отмечалось, возможны несколько путей минимального веса и несколько путей минимальной длины (напомним, что вес пути – это сумма весов всех его ребер, а длина – число ребер). Поэтому возникает задача найти одновременно путь минимального веса и минимальной длины. Здесь возможны несколько различных постановок задачи: а) поиск одного (любого) пути минимального веса среди всех путей минимальной длины; б) поиск всех путей минимального веса среди всех путей минимальной длины; в) поиск одного (любого) пути минимальной длины среди всех путей минимального веса; г) поиск всех путей минимальной длины среди всех путей минимального веса. Напомним, что алгоритм GenTree(G, VH, VK) по графу G строил подграф G1, в котором все пути из VН в VК имеют одинаковую минимальную длину. Если к подграфу G1 применить алгоритм Dijkstra(G1, VH, VK), получится решение задачи а). Если же к G1 применить алгоритм GenDijkstra(G1, VH, VK), это будет решением задачи б). Аналогично алгоритм Dijkstra(G, VH, VK) по графу G строил подграф G2, в котором все пути из VН в VК имеют одинаковый минимальный вес. Если применить алгоритмы Tree(G2, VH, VK) и GenTree(G2, VH, VK) к G2, будут решены задачи в) и г). Система навигации Предложенные авторами алгоритмы поиска кратчайших маршрутов были апробированы при создании системы навигации для космического видеотренажера. Данный тренажер использует систему GLView визуализации трехмерных виртуальных сцен и входит в состав имитационно-тренажерного комплекса подготовки космонавтов к работе на МКС. Для выбора начала маршрута необходимо навести указатель на соответствующий поручень визуализированной виртуальной модели космической станции и нажать левую кнопку мыши (при этом данный поручень подсвечивается). Аналогично можно задать и конечный поручень пути. При наведении указателя на поручень на экране также высвечивается имя этого поручня. После выбора двух поручней между ними автоматически будут построены один или все (в зависимости от поставленной задачи) кратчайшие (по длине или по весу) маршруты. Для отображения первого построенного пути между двумя поручнями осуществляется подсветка поручней, входящих в маршрут, заданным цветом. Нажатием клавиши P на клавиатуре можно осуществлять поочередную подсветку альтернативных путей. Будущие разработки Для обеспечения большей реалистичности имитируемой окружающей обстановки и проведения более эффективного обучения специалистов в тренажерных комплексах подготовки космонавтов целесообразно применять технологию виртуальной реальности. Эта технология включает в себя использование стереовизуализации в шлемах виртуальной реальности, а также специальных компьютерных перчаток. На экраны шлема осуществляется вывод изображений, синтезированных на компьютере и аналогичных тому, что видит космонавт при работе как внутри, так и на поверхности станции. Изображения в шлеме зависят от положения наблюдателя и направления его взгляда. Поскольку определение последнего параметра является достаточно трудоемкой задачей, вместо него можно учитывать направленность головы. Эти параметры можно вычислить с использованием специальных систем трекинга. Компьютерные перчатки применяют для обеспечения взаимодействия тренирующегося человека с виртуальной средой. Они позволяют отслеживать положение, а также действия рук и пальцев. Кроме того, использование таких перчаток дает возможность реализации обратной связи (тактильных ощущений). Перспективной задачей в области тренажерных комплексов подготовки космонавтов является создание системы, одновременно использующей шлемы виртуальной реальности, компьютерные перчатки и систему навигации. При этом модели рук в виртуальном пространстве должны повторять движения реальных рук и пальцев. Производя движения руками и сгибая пальцы, тренируемый космонавт сможет брать в виртуальные руки различные объекты трехмерной сцены, захватывать поручни и перемещаться по ним. Система навигации будет подсказывать правильное направление движения, подсвечивая следующий по маршруту поручень, в зависимости от текущего положения наблюдателя. Небольшая модификация предложенных алгоритмов поиска пути между двумя поручнями позволит осуществлять выбор маршрута, проходящего через заданный поручень. Кроме того, в ходе обучения система навигации сможет воспроизвести движение космонавта по выбранному пути. Итак, в данной статье были предложены и подробно рассмотрены новые алгоритмы поиска одного или всех возможных маршрутов (удовлетворяющих критерию минимальной длины или критерию наименьшей сложности прохождения) между двумя заданными поручнями на модели МКС. На основе описанных алгоритмов была разработана система навигации для космического видеотренажера, позволяющая повысить эффективность подготовки специалистов для работы на внешней стороне станции. Литература 1. Михайлюк М.В., Торгашев М.А. Система «GLView» визуализации для моделирующих комплексов и систем виртуальной реальности // Вест. РАЕН. 2011. Т. 11. № 2. С. 20–28. 2. West D.B. Introduction to Graph Theory. Prentice Hall, 1996. 3. Zhan F. Benjamin; Noon, Charles E. Shortest Path Algorithms: An Evaluation Using Real Road Networks. Transportation Science, 1998, Vol. 32 (1), pp. 65–73. 4. Cormen T.H., Leiserson C.E., Rivest R.L. Introduction to Algorithms. MIT Press and McGraw-Hill, 2001. 5. URL: http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm (дата обращения: 21.05.2012). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3217 |
Версия для печати Выпуск в формате PDF (7.64Мб) Скачать обложку в формате PDF (1.33Мб) |
| Статья опубликована в выпуске журнала № 3 за 2012 год. [ на стр. 68-73 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Удаленное управление роботизированным устройством с использованием технологий виртуальной реальности
- Использование спутникового позиционирования для системы автоматического управления локомотивами на сортировочных станциях
- Представление графов и неориентированных гиперграфов с ограничениями в реляционной базе данных
- Модель группировки радиоэлектронных систем для оценки временных показателей надежности
- Тренажер для реабилитации пациентов с проблемами мобильности руки, построенный с использованием технологий виртуальной реальности
Назад, к списку статей



 [0, n-1]) объекта-поручня в виртуальной сцене, номер ik соответствующей ему вершины графа G и список номеров вершин, связанных ребром с вершиной ik.
[0, n-1]) объекта-поручня в виртуальной сцене, номер ik соответствующей ему вершины графа G и список номеров вершин, связанных ребром с вершиной ik.
 Проиллюстрируем работу предложенного алгоритма с помощью графа G, изображенного на рисунке 1. Допустим, что необходимо построить кратчайший маршрут из вершины V6 в вершину V1. Из рисунка видно, что G содержит три пути (без циклов) из V6 в V1, при этом два из них (V6àV3àV2àV1 и V6àV7àV2àV1) включают по 3 ребра и один (V6àV5àV4àV3àV2àV1) – 5 ребер.
Проиллюстрируем работу предложенного алгоритма с помощью графа G, изображенного на рисунке 1. Допустим, что необходимо построить кратчайший маршрут из вершины V6 в вершину V1. Из рисунка видно, что G содержит три пути (без циклов) из V6 в V1, при этом два из них (V6àV3àV2àV1 и V6àV7àV2àV1) включают по 3 ребра и один (V6àV5àV4àV3àV2àV1) – 5 ребер.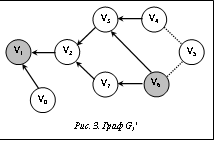 Рассмотрим нахождение всех кратчайших маршрутов между вершинами VH и VK графа G. Пусть P(V) – массив ссылок на родителей вершины V, P(V)[i] – i-й родитель V; LS – конечный уровень, при достижении которого алгоритм должен завершить работу (вначале равен большому положительному числу); size(A) – число элементов в массиве A; M – массив кратчайших путей, M[k] – k-й кратчайший путь, содержащий индексы входящих в него вершин. Тогда получаем следующий алгоритм GenTree(G, VH, VK) поиска всех кратчайших путей между вершинами VH и VK в графе G.
Рассмотрим нахождение всех кратчайших маршрутов между вершинами VH и VK графа G. Пусть P(V) – массив ссылок на родителей вершины V, P(V)[i] – i-й родитель V; LS – конечный уровень, при достижении которого алгоритм должен завершить работу (вначале равен большому положительному числу); size(A) – число элементов в массиве A; M – массив кратчайших путей, M[k] – k-й кратчайший путь, содержащий индексы входящих в него вершин. Тогда получаем следующий алгоритм GenTree(G, VH, VK) поиска всех кратчайших путей между вершинами VH и VK в графе G.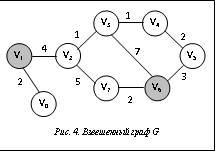 В S находим неотмеченную вершину Vt с минимальным весом;
В S находим неотмеченную вершину Vt с минимальным весом; до
до  с записью в память индексов вершин, входящих в искомый кратчайший путь.
с записью в память индексов вершин, входящих в искомый кратчайший путь.