Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование газового режима литейной формы
Аннотация:
Abstract:
| Авторы: Матохина А.В. () - , Воронин Ю.Ф. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 12422 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Газовый режим литейной формы существенно влияет на формирование качества отливок. Материалом, из которого изготавливаются формы и стержни, обычно служит песок и глина. В результате теплового воздействия залитого металла на песчаную форму, из нее выделяются газы, образующиеся при испарении воды, горении органических материалов и др. Часть возникающих газов удаляется естественным путем через знаковые части формы и стержня, другая часть проникает в залитый металл и приводит к образованию различных газовых дефектов. Самый распространенный дефект – газовые раковины, которые образуются при давлении, превышающем некоторый критический порог. Этой проблеме посвящен ряд работ, в которых получены математические модели газового режима, описывающие газовые выделения из стержней и форм, имеющих простейшее геометрическое строение (цилиндр, конус), также допускаются существенные ограничения (например, металл заливается мгновенно). В литературе предлагаются различные математические формулы для описания газового режима формы в точке контакта металл-форма, не позволяющие анализировать детали сложной геометрии. Авторами была разработана математическая модель расчета давления газа при изготовлении отливки произвольной конфигурации. Эта модель позволяет определить время заливки формы для предотвращения образования газовых дефектов с учетом следующих факторов:
где Для нахождения давления как функции времени используется следующая формула:
Аналитическая реализация данной модели невозможна, поскольку приходится сталкиваться с функциями и уравнениями, решение которых возможно только численными методами, например, возникают такие задачи, как нахождение площади поверхностной формы и стержня сложной конфигурации или кусочно-линейная интерполяция функций по имеющимся значениям. Для реализации математической модели потребовались: - язык программирования Borland C++ Buil- der 6, с помощью которого был создан интерфейс проекта и проводились все необходимые численные расчеты; - графический пакет AutoCAD 2002, который используется для формирования файла с данными геометрической формы 3D-модели отливки. Программа считывает данные из файла, преобразует в систему исчисления СИ (так как в AutoCAD, например, мерой длины является миллиметр), для удобства вычисления отсчет высоты начинается с нуля (если даже нижняя грань по оси сечения имеет отрицательное значение). По полученным значениям строятся кусочно-линейные функции Пформы(h), Пстержня(h) и Fзм(h). С их помощью считается площадь поверхности формы и стержня. Для нахождения зависимости всех полученных функций от времени необходимо найти зависимость высоты от времени. Используя формулы математической модели, находим функцию U(h), отсюда h=U-1(Gmτ) получаем через нахождение обратной функции. Далее считываются параметры, вводимые с терминала, и данные, соответствующие выбранному пользователем типу формовочной смеси и металла.
где n – показатель степеней кривой (параболы, описывающей температуру поля формы); a2 – коэффициент температуропроводности формовочной смеси; tд – температура деструкции связующего; tп – температура заливки металла; t0 – начальная температура формы или стержня; Г – абсолютная газотворная способность смеси, которая определяется опытным путем в лабораториях заводов для каждого замеса. Для нахождения объема опор в области фильтрации V используется формула: V=E*W, где W – объем стержня или формы в области фильтрации; Е – пористость смеси. Из физического смысла и ограничений Sзн>Fпр>Sпов.ст были предложены зависимости: Fпр.ф=Sпов.ф, где Fпр.ф и Fпр.ст – сечение газового потока формы и стержня; Sпов.ф и Sпов.ст – площадь поверхности формы и стержня соответственно; Sзн – площадь знака стержня. Когда все дополнительные вычисления сделаны, приступаем к определению оптимального времени заливки. Для этого фиксируем одно из значений τз из интервала времени 0<τз<τзатв и решаем нелинейное уравнение для определения оптимального времени заливки относительно переменной τ, при τ> τз. Процесс происходит в два этапа: 1) находим промежуток времени, на котором функция, стоящая в левой части уравнения, меняет знак; 2) методом деления пополам находим такое время заливки τз, при котором значение функции равно нулю с точностью Е=0,000001. Далее полученные значения τ и τз подставляем в формулу для нахождения давления и проверяем, на сколько значение давления р отличается от оптимального. Если значение не удовлетворяет данному условию, корректируем время заливки. Снова по фиксированному τз находим τ и опять делаем проверку. Эти действия повторяем до тех пор, пока не найдем решение или пока время заливки τз не превысит время образования корочки металла τзатв. В первом случае на экране появится результат, во втором будет выведено сообщение, что оптимизация невозможна и стоит изменить вводимые параметры, например, длину пути фильтрации или газопроницаемость смеси. Автоматизированная система на основе построенной математической модели, архитектура которой представлена на рисунке, состоит из следующих основных окон: - главное окно с меню "Газовый режим в литейной форме"; - окно для выбора металла и формовочной смеси с отображением значений каждого параметра "Свойства"; - окно для ввода необходимых данных "Параметры для расчета"; - окно со списком металлов "Работа с базой данных металлов"; - окно с параметрами пользователя для расчетов давлений газа в конкретной литейной форме "Собственные параметры". Основная работа происходит с окном "Газовый режим в литейной форме", его пользователь видит после запуска программы, остальные окна появляются при вызове их из меню или щелчком по кнопке на панели инструментов. Для удобства и простоты использования интерфейс был создан под руководством специалиста в области литейных технологий. Автоматизированная система на основе построенной математической модели помогает производить отладку технического процесса изготовления отливки вне литейного цеха, что позволяет уменьшить процент брака, обеспечить получение литья высокого качества. В программе приведена развернутая информация по газовому режиму в литейной форме с анимированной моделью процесса образования и вывода, что позволяет использовать ее для обучения на ряде предприятий России. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=342 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Компьютер - хранитель домашнего очага
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Разработка корпоративной базы в области химии и химической технологии
- К вопросу параметризации свойств программных средств обучения
- Функционально-информационные модели бухгалтерского учета
Назад, к списку статей



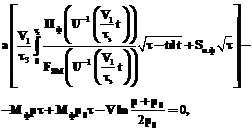
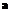 – относительный коэффициент газовыделения;
– относительный коэффициент газовыделения;  – объем металла в форме на уровне h (изменяется от нуля до
– объем металла в форме на уровне h (изменяется от нуля до 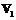 );
);  – площадь зеркала металла на высоте t;
– площадь зеркала металла на высоте t; 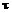 – время от начала заливки;
– время от начала заливки;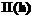 – периметр формы на высоте h;
– периметр формы на высоте h;  – элементарная площадка, примыкающая к периметру смачивания; Мф – пропускная способность; p – абсолютное давление газа на поверхности контакта с металлом;
– элементарная площадка, примыкающая к периметру смачивания; Мф – пропускная способность; p – абсолютное давление газа на поверхности контакта с металлом;  – абсолютное давление газа на открытой поверхности формы, часто равное атмосферному.
– абсолютное давление газа на открытой поверхности формы, часто равное атмосферному.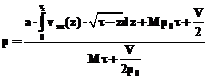 , где
, где  – функция скорости подъема металла от времени.
– функция скорости подъема металла от времени.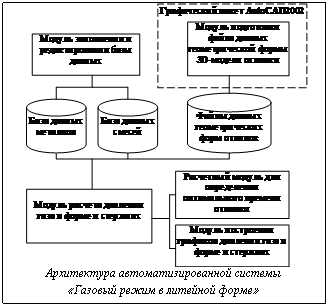 Используя данные, указанные пользователем, проводим дополнительные вычисления параметров для формы и стержней: а, V, M, Fпр.ф и Fпр.с. Здесь а – относительный коэффициент газовыделения, который рассчитывается по формуле:
Используя данные, указанные пользователем, проводим дополнительные вычисления параметров для формы и стержней: а, V, M, Fпр.ф и Fпр.с. Здесь а – относительный коэффициент газовыделения, который рассчитывается по формуле: ,
, ,
,