Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Имитационное моделирование пневмогидромеханической системы в компьютерном тренажере
Аннотация:Имитационное моделирование динамических процессов и систем находит все большее применение в компьютерных тренажерах. В статье изложены принципы построения имитационной модели функционирования пневмоги-дромеханической системы, используемой в компьютерном тренажере. При функционировании моделируемой системы в ней может одновременно происходить перемещение жидкости, газа, физического тела. Расчет расхода жид-кости и газа производится исходя из того, что течение жидкости происходит в турбулентном квадратичном режиме, а течение газа – со скоростью, меньшей скорости звука.Изменения количества газа и жидкости в емкостях моделируемой системы рассчитываются на основе конечно-разностных уравнений, после чего определяется давление, установившееся в системе. Имитационная модель реализована в виде библиотеки на VC++. Программа тренажера каждые 100 мс передает в библиотеку параметры системы и получает вычисленные значения давлений и распределение жидкости и газа в системе. Созданная имитационная модель системы адекватно описывает изменения потоков и давлений, перенос вещества в различных режимах.
Abstract:Simulation modeling of dynamic processes and systems is becoming more popular in computer simulators. The article sets out the principles of building a simulation model of a functioning air-hydro-mechanical system utilized in a computer simulator. The modeled system functioning may be characterized by simultaneous movement of liquid, gas, a physical body. The liquid and gas flow calculation is based on the fact that the liquid flows in the turbulent quadratic mode, whereas the gas flows at velocity below the sonic speed. Thechange of the gas and liquid quantity in the tanks of the mod-eled system are calculated based on the finite-differenceequations, and then the steady-state pressure is determined in the system. The simulation model has been implemented as a VC++ library. Each 100 ms the simulator program transfers the system parameters into the library and receives computer pressure values and liquid and gas distribution in the system. The generated simulator model of the system adequately describes changes in the flows and pressures, mass transfer in various modes.
| Авторы: Иванов В.В. (ivanovsl-tver@mail.ru) - НИИ «Центрпрограмсистем», г. Тверь, Россия, Лаленков В.А. () - НИИ «Центрпрограмсистем» (зав. отделом ), Тверь, Россия | |
| Ключевые слова: гидродинамика., пневматика, имитационное моделирование, тренажеры, программирование |
|
| Keywords: hydrodynamics, pneumatics, simulation, simulators, programming |
|
| Количество просмотров: 10808 |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
Компьютерный тренажер, представляющий собой совокупность аппаратных и программных средств, предназначен для подготовки специалистов к выполнению действий по управлению материальными объектами и системами. При разработке тренажера необходимо создать адекватную имитационную модель системы, в которой можно выделить две основные взаимосвязанные части: 1) имитация органов управления, пультов и их индикаторных процессов, с которой непосредственно взаимодействует обучаемый; 2) имитация физических процессов, протекающих в моделируемой системе при ее функционировании. Моделируемая пневмогидромеханическая система (ПГМС), схематично изображенная на рисунке, представляет собой совокупность органов управления, клапанов, датчиков, емкостей, трубопроводов и т.д. Система имеет связи с внешними источниками газа и жидкости (магистральными трубопроводами, помещениями, атмосферой, водоемом). При проведении тех или иных операций по элементам ПГМС происходит перетекание жидкости и газа, для их имитации на компьютере необходимо предварительно перейти от дифференциальных к конечно-разностным уравнениям. Физико-математическая модель работы системы описывает процессы функционирования системы во времени, перемещение жидкости и газа, изменение давления в различных режимах. Модель системы включает в себя уравнения зависимости расхода жидкости и газа от давления на концах трубопроводов, а также уравнения материального баланса. Каждая емкость k характеризуется объемом Vk, давлением pk, массой газа mвk и объемом жидкости Vжk, в ней находящейся. Для имитации упругих свойств емкости и жидкости с каждой емкостью связывается упругое тело, имеющее объем Vрk и модуль Юнга E. Величина деформации ΔVрk этого тела связана с давлением pk внутри емкости выражением Поскольку отдельные емкости соединяются трубопроводами с внешними источниками газа или жидкости, для расчета необходимо задать давление жидкости (Pж) и газа (Pг, Php, Pmp,) во внешних источниках. Емкости могут через трубопровод соединяться с помещением, такое помещение можно представить как емкость с объемом VП, давлением pП, массой газа mП и объемом жидкости VжП . Если в емкости i находится выталкиваемое тело с массой MП и сечением SП, для описания процессов в такой емкости добавляется VCi – свободный объем в емкости.
На основе анализа состояния датчиков, клапанов трубопроводной системы, разницы давления на концах трубопроводов определяется, по каким трубопроводам и в каком направлении перемещаются жидкость или газ. Выбор формул для расчета расхода жидкости и газа определяется числом Рейнольдса Re, которое находится следующим образом: Анализ моделируемой системы показал, что течению жидкости в трубопроводах соответствует турбулентный квадратичный режим с числом Re>104, течение газа происходит со скоростью, меньшей скорости звука, а коэффициент гидравлического трения λij можно считать постоянным. Массовый расход газа и его направление в трубопроводе ij определяются по формуле
Объемный расход жидкости и его направление в трубопроводе ij определяются перепадом давления на его концах по формуле Если емкости i и j не соединяются между собой, то Tвij=Tжij=0. При расчете расхода жидкости плотности r следует учитывать дополнительную разность давления Δpij, связанную с разницей уровней жидкости в емкостях Δhij, определяемую выражением Dpij=Dhijrg, где g – ускорение свободного падения. Для каждой емкости вычисляются суммарные расход жидкости и газа. Суммарный расход может быть как положительным, так и отрицательным, соответственно увеличивающим или уменьшающим массу газа или объем жидкости в емкости. Суммарный массовый расход газа QMk для емкости k:
где Ki=1, если трубопровод i соединен с емкостью k, по нему происходит перетекание газа (открыт соответствующий клапан) и на его втором конце находится газ под давлением pi>pk, иначе Ki=0; Kj=1, если трубопровод j соединен с емкостью k, на его конце, соединенном с емкостью, находится газ, по нему происходит перетекание газа (открыт соответствующий клапан) и на его втором конце давление pj Суммарный объемный расход жидкости QVk для емкости k:
где Ki=1, если трубопровод i соединен с емкостью k, по нему происходит перетекание жидкости (открыт соответствующий клапан) и на его втором конце находится жидкость под давлением pi>pk, иначе Ki=0; Kj=1, если трубопровод j соединен с емкостью k, на его конце, соединенном с емкостью, находится жидкость, по нему происходит перетекание жидкости (открыт соответствующий клапан) и на его втором конце давление pj < pk, иначе Kj=0. Величины Tжji и Tвij уточнялись при верификации имитационной модели. Объем жидкости и масса газа, поступившие в емкость или истекшие из нее, равны произведению соответствующих суммарных расходов на малый интервал модельного времени Δt. При этом, если истекающие объем жидкости и масса газа меньше объема жидкости и массы газа, имеющихся в емкости, или если объем жидкости превысил объем емкости, модельный интервал времени Δt уменьшается и производится перерасчет по всей модели ПГМС. Величина модельного интервала времени Δt выбирается в пределах от 0,1 мкс до 1 мкс. Масса газа в емкости k через Δt будет равна mвk=mвk+QMkΔt, объем жидкости Vжk=Vжk+QVkΔt. Если mвk¹0 и Vжk¹0, установившееся давление p¢k в емкости определяется положительным решением уравнения
Если mвk=0 (в емкости только жидкость), установившееся давление определяется выражением
В модели задано, что изменение давления Dpk в емкости за модельный интервал времени Δt не должно превышать наперед заданное значение ΔP (103 Па), в случае нарушения этого условия модельный интервал времени Δt уменьшается и производится перерасчет по всей модели ПГМС. Движение тела массой MП с площадью поперечного сечения SП в цилиндрической емкости будет происходить под действием разницы давления DpП=Рж–p1. Ускорение aПi, скорость vПi и смещение ΔsПi тела вычисляются следующим образом: aПi=DpПSП/МП, vПi=vПi-1+aПiΔt, ΔsПi=vПi-1Δt+ Имитационная модель реализована в виде библиотеки на VC++ с использованием объектно-ориентированного подхода. Библиотека содержит данные о структуре моделируемой системы: описание емкостей, их соединение трубопроводами между собой, с другими источниками жидкости или газа, внешней средой. Начальные параметры моделируемой системы, давление и заполнение емкостей задаются при запуске тренажера. Интерфейс оператора, состоящий из панелей управления и контроля, задает и отображает состояние моделируемой системы. Состояние имитируемых органов управления (переключателей, манипуляторов, вентилей) преобразуется в набор входных параметров для имитационного моделирования процессов. Расчетная часть библиотеки выполнена в виде последовательно выполняемых библиотечных функций вычисления расхода, изменения массы газа и объема жидкости, установившихся давлений. Программа тренажера через равные интервалы времени ΔT=100 мс передает в библиотеку параметры Vk, Vжk, pk по каждой емкости, признаки открытия клапанов трубопроводов и наличия жидкости или газа на концах трубопроводов. По завершении расчета библиотека возвращает в программу тренажера вычисленные значения V¢жk и p¢k для каждой емкости, а также величины, описывающие движение тела массы MП. Исследование и оценка имитационной модели проводились на основе сопоставления времени выполнения различных операций в имитационной модели и в реальной системе. Имитационная модель показала свою пригодность для ее практического использования в компьютерных тренажерах. Предложенные принципы построения физико-математической модели могут использоваться для моделирования разнообразных пневмогидродинамических систем. Литература 1. Советов Б.Я., Яковлев С.А. Моделирование систем: учеб. для вузов. М.: Юрайт, 2012. 2. Павловский Ю.Н. Имитационное моделирование. М.: Издат. центр «Академия», 2008. 3. Аметистов Е.В., Григорьев В.А., Емцев Б.Т. Тепло- и массообмен. Теплотехнический эксперимент: справочник. М.: Энергоиздат, 1982. 4. Маршалов Е.Д., Нечаева О.А. Имитационное моделирование гидравлических систем с регулирующими органами // Вестн. ИГЭУ. Иваново. 2007. Вып. 4. References 1. Sovetov B.Ya., Yakovlev S.A., Modelirovanie sistem [System Modeling], 4th ed., revised and enlarged, Moscow, Yurayt, 2012. 2. Pavlovsky Yu.N., Imitatsionnoe modelirovanie [Simulation Modeling], Moscow, Academiya publ. center, 2008. 3. Ametistov E.V., Grigoriev V.A., Emtsev B.T., Teplo- i massoobmen. Teplotekhnicheskiy eksperiment: spravochnik [Heat- and mass exchange. Heat Engineering Experiment: guidebook], Moscow, Energoizdat, 1982. 4. Marshalov E.D., Nechaeva O.A., Vestnik IGEU [The Bulletin of IGEU], iss. 4, Ivanovo, 2007. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3600 |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
| Статья опубликована в выпуске журнала № 3 за 2013 год. [ на стр. 260-263 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Система моделирования поведения групп робототехнических агентов с элементами социальной организации Кворум
- Универсумная методика описания процесса разработки программного обеспечения
- О программе расчета потерь электроэнергии в радиальных электрических сетях
- Некоторые результаты имитационного моделирования мультисервисных бортовых цифровых платформ стандарта DVB-RCS
- Разработка специального программного обеспечения для ввода исходных данных при имитационном моделировании
Назад, к списку статей



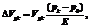 где p0 – атмосферное давление.
где p0 – атмосферное давление.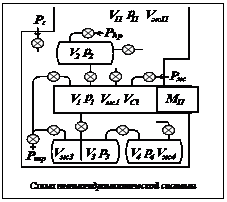 Каждый трубопровод ij, соединяющий емкости i и j (i¹j), характеризуется диаметром dij, длиной lij, коэффициентом гидравлического трения λij, наличием на концах клапанов, жидкости или газа.
Каждый трубопровод ij, соединяющий емкости i и j (i¹j), характеризуется диаметром dij, длиной lij, коэффициентом гидравлического трения λij, наличием на концах клапанов, жидкости или газа.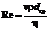 , где v – скорость среды в трубе; ρ – плотность среды; dтр – внутренний диаметр трубы; η – коэффициент динамической вязкости среды.
, где v – скорость среды в трубе; ρ – плотность среды; dтр – внутренний диаметр трубы; η – коэффициент динамической вязкости среды.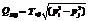 , здесь
, здесь 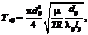 где pi, pj – давление на концах трубопровода (pi>pj); μ – молярная масса газа; T – температура газа; R – универсальная газовая постоянная.
где pi, pj – давление на концах трубопровода (pi>pj); μ – молярная масса газа; T – температура газа; R – универсальная газовая постоянная.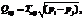 здесь
здесь 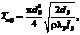 где pi, pj – давление на концах трубопровода (pi>pj); ρ – плотность жидкости.
где pi, pj – давление на концах трубопровода (pi>pj); ρ – плотность жидкости.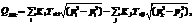
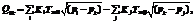
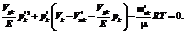
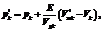 Dpk=½p¢k–pk½.
Dpk=½p¢k–pk½.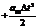 , при этом свободный объем в емкости VCi за модельный интервал времени Δt изменится на ΔVПi = ΔsПiSП и VCi = VCi-1 + ΔVПi.
, при этом свободный объем в емкости VCi за модельный интервал времени Δt изменится на ΔVПi = ΔsПiSП и VCi = VCi-1 + ΔVПi.