Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Подготовка детализированной текстуры поверхности для высокореалистичной визуализации Земли
Аннотация:Одним из основных критериев обеспечения высокой реалистичности изображений при визуализации модели Земли в имитационно-тренажерных комплексах подготовки космонавтов является использование в процессе рендеринга детализированной текстуры земной поверхности. В данной статье предлагаются технология подготовки такой текстуры из исходного набора тайлов (фотоизображений небольших участков земной поверхности) одинакового размера для ее дальнейшего применения в приложениях, созданных для визуализации моделей Земли и использующих системы распределенных вычислений, а также технология сверхбольших текстур. В рамках проблемы рассматривается решение ее наиболее существенных задач. Поскольку, как правило, исходные тайлы заданы в проекции Меркатора, в работе предлагается и подробно разбирается алгоритм преобразования текстуры с проекцией Меркатора в удобную для последующего использования текстуру с эквидистантной цилиндрической проекцией. Также рассматривается способ для бесшовного добавления в подготавливаемую текстуру водных поверхностей в случае их отсутствия в исходном наборе тайлов, заключающийся в использовании специальной текстурной маски в градациях серого цвета. Метод создания такой маски предложен и описан в одном из разделов данной статьи. Кроме того, в работе рассматривается созданный на основе предлагаемых технологий, методов и алгоритмов программный комплекс. Комплекс состоит из трех приложений, работающих под управлением операционной системы Microsoft Windows, и одного сценария для программы Adobe Photoshop, которые в совокупности позволяют пользователю за несколько шагов подготовить требуемую текстуру земной поверхности.
Abstract:One of the main criteria for providing highly realistic images when Earth model is rendered in the simulation-training complexes is to use Earth's detailed surface texture in visualization process. This paper proposes such texture preparation technology from initial set of same size tiles (photo images of Earth's small surface area). This texture can be subsequently used in applications that visualize Earth models and use distributed computing as well as ultra-large texture technology. The article consideres the decisions of the most important tasks regarding the described problem. Since original tiles are usually set in the Mercator projection, the algorithm is proposed to transform Mercator projection texture to equidistant cylindrical projection texture which is easier to use hereinafter. Also the way for seamless adding water surfaces to prepare texture is described if they are absent in the original set of tiles. It includes using special grayscale mask texture. The method of such a mask creation is proposed and described in one of the sections of this article. In addition, in the paper describes the software complex that has been created based on proposed technologies, methods and algorithms. This complex consists of three applications for Microsoft Windows operating system and one script for the Adobe Photoshop program. They allow user to prepare a required texture of Earth’s surface in a few steps.
| Авторы: Мальцев А.В. (avmaltcev@mail.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, кандидат физико-математических наук | |
| Ключевые слова: видеотренажеры, текстурирование, модели планет, высокореалистичная визуализация |
|
| Keywords: video trainers, texturing, planet models, high realistic visualization |
|
| Количество просмотров: 9686 |
Версия для печати Выпуск в формате PDF (7.95Мб) Скачать обложку в формате PDF (1.45Мб) |
Важным требованием, предъявляемым к имитационно-тренажерным комплексам в различных научно-технических областях, является высокая реалистичность визуализируемых на компьютере трехмерных виртуальных моделей. В космических тренажерных системах к таким объектам относятся, например, Международная космическая станция (МКС), транспортные и грузовые корабли, Земля. Каждый из них играет существенную роль в правильном восприятии окружающей обстановки. Для обеспечения высокой реалистичности синтезируемых изображений Земли необходимо иметь детализированную текстуру ее поверхности. В данной статье рассматривается задача син- теза детализированной текстуры высокого разрешения для модели Земли, визуализируемой с использованием распределенных вычислительных систем и технологии сверхбольших текстур [1]. В качестве исходных данных берется набор тайлов – фотоизображений небольших участков земной поверхности. Все тайлы имеют одинаковый размер (в пикселах) и представлены в проекции Меркатора WGS84 (свойства данной проекции будут рассмотрены далее). Отметим, что обычно исходные наборы, как свободно распространяемые, так и доступные для коммерческого использования, не включают в себя крупные водные поверхности (озера, моря, океаны), что выражается в отсутствии тайлов, вообще не содержащих суши. В результате необходимо получить полную (то есть описывающую всю поверхность Земли) текстуру с эквидистантной цилиндрической проекцией. Для решения такой задачи в работе предлагаются алгоритм преобразования текстур высокого разрешения из проекции Меркатора в эквидистантную проекцию, а также технология бесшовного добавления в подготавливаемую текстуру отсутствующих в исходных данных водных поверхностей, обеспечивающая плавный переход между ними и сушей. Технология создания детализированной текстуры Земли Для решения задачи генерации детализированной текстуры Земли предлагается следующий алгоритм. На первом этапе необходимо осуществить сборку имеющихся тайлов в единое изображение M высокого разрешения. При этом участки водной поверхности, для которых отсутствуют тайлы, заполним черным цветом. Для хранения и обработки текстуры М применим формат данных Photoshop RAW 24 бит/пиксел (по 8 бит на каждую из цветовых компонент R, G, B). Исходные изображения, а значит и текстура М, представлены в проекции Меркатора [2] – равноугольной картографической проекции, сохраняющей углы между направлениями. Меридианы в ней обозначаются параллельными равноотстоящими линиями, а параллели – параллельными линиями, расстояние между которыми увеличивается при движении от экватора к полюсам. В связи с тем, что формула отображения координат на эллипсоиде в координаты на плоскости содержит функцию тангенса, аргумент которой при приближении к полюсам стремится к π/2, сами полюсы не могут быть представлены на проекции Меркатора. Поэтому обычно такую карту ограничивают областями до 80–85° северной и южной широты. Масштаб на карте Меркатора не является постоянным, он увеличивается от экватора к полюсам (как обратный косинус широты). Для применения создаваемой текстуры при визуализации модели Земли удобно использовать другой вид проекции – эквидистантную цилиндрическую [2]. Она является равнопромежуточной, то есть и меридианы, и параллели представляют собой равноудаленные прямые линии, а масштаб сохраняется при движении от экватора к полюсам. В отличие от проекции Меркатора данная проекция охватывает широтный интервал от 90° северной до 90° южной широты, а значит, включает полюсы. Для преобразования имеющейся текстуры М с проекцией Меркатора в текстуру E с эквидистантной цилиндрической проекцией в данной статье предлагается специальный алгоритм. На втором этапе необходимо подготовить дополнительную текстуру T (такого же размера в пикселах, что и E), на основе которой будут добавляться водные поверхности к созданной текстуре Е. T является модифицированным вари- антом так называемой текстуры маски земной поверхности, в которой белым цветом (1,0 в числовом эквиваленте) отображается суша, а черным (0,0) – водные поверхности. Использование черно-белого варианта маски отразилось бы в ярко выраженных границах между сушей в текстуре E и добавленными к ней водными поверхностями. Чтобы избежать резких цветовых границ и получить сглаженные переходы от суши к воде, в данной работе предлагается применять маску T в градациях серого цвета (в отрезке [0,0, 1,0]). Метод ее получения из исходного черно-белого изображения описан далее.
где Ei,j – исходный цвет рассматриваемого пиксела; Ti,j – числовой эквивалент цвета соответствующего пиксела маски; Cw – цвет водной поверхности. Цвет Cw может быть задан постоянной величиной или браться из соответствующего пиксела дополнительной, менее детальной, но полной текстуры земной поверхности (в той же цилиндрической проекции), приведенной к эквивалентному Е размеру в пикселах. Добавление водных поверхностей осуществляется практически без швов и обеспечивает возможность сохранения цвета прибрежного шельфа, если он имеется в исходном наборе тайлов. Таким образом, приходим к следующей технологии создания текстуры земной поверхности. I. Подготовка детализированной текстуры Земли без водных поверхностей: – сборка исходных тайлов в текстуру M; – преобразование М из проекции Меркатора в эквидистантную цилиндрическую проекцию с получением новой текстуры E. II. Подготовка текстуры маски: – приведение исходной черно-белой текстуры T ' маски к размеру E; – модификация T ' с получением маски в градациях серого, размывающей резкую цветовую границу между прибрежным шельфом в текстуре Е и добавляемой к ней водной поверхностью. III. Добавление водных поверхностей с учетом подготовленной маски. Рассмотрим подробнее алгоритм преобразования текстуры с проекцией Меркатора в текстуру с эквидистантной цилиндрической проекцией, а также метод создания необходимой текстуры T маски в градациях серого цвета (рис. 1). Преобразование проекции Пусть М (рис. 1а) – текстура земной поверхности с проекцией Меркатора, имеющая размер Wm´Hm пикселов (Wm и Hm кратны 2); Xm и Ym – оси системы координат Меркатора; Im и Jm – оси системы координат для индексирования пикселов из M. Начальные точки обеих систем совпадают и находятся в середине карты M. Кроме того, пусть результирующая текстура E с эквидистантной цилиндрической проекцией (рис. 1б) имеет размер We ´He пикселов, Xe и Ye – оси широтно-долготной системы координат, Ie и Je – оси системы координат для индексирования пикселов из E. Начальные точки этих систем также совпадают и располагаются в центре текстуры E. Отметим, что для эквидистантной цилиндрической проекции характерно соотношение 2:1 ширины и высоты карты [2], то есть He=We/2. Чтобы при преобразовании сохранить исходное разрешение текстуры по оси абсцисс, возьмем We = Wm. Предположим, что имеющаяся текстура M создана с учетом эллипсоидной формы Земли. Поэтому для преобразования проекции возьмем за основу формулы перевода широты φ и долготы λ для эквидистантной цилиндрической проекции в координаты xm и ym карты Меркатора для эллипсоида [2, 3]: xm=al,
где Введем коэффициент масштабирования ρm для пересчета непрерывных координат ym карты Меркатора в дискретные координаты jm пикселов имеющейся у нас текстуры земной поверхности в проекции Меркатора:
где скобки обозначают целую часть числа. Аналогично пусть коэффициент масштабирования ρe для пересчета непрерывных широтных координат (в радианах) в дискретные координаты jе пикселов текстуры земной поверхности в эквидистантной цилиндрической проекции равен
Поскольку, как упоминалось ранее, представленные в карте Меркатора максимальная φmax и минимальная φmin широты составляют не более 85° северной и южной широты соответственно, при преобразовании проекции текстура M отобразится только в центральную область U (с индексами jeÎ[je,min, je,max]) текстуры E, содержащей широты φÎ[-90°, 90°] (рис. 2). Используя формулу (3), получим Области текстуры E, лежащие за пределами U, закрасим в черный цвет. Они будут обработаны в дальнейшем на этапе добавления водных поверхностей. Для формирования области U необходимо определить соответствие ее пикселов пикселам текстуры M. Поскольку и карта Меркатора, и эквидистантная проекция охватывают долготный диапазон [-π, π], We=Wm, а масштаб карты Меркатора по оси Y растет от экватора к полюсам, каждому пикселу (ie, je)ÎU соответствует отрезок R из некоторого числа r пикселов (im, jm,k)ÎМ, где im=ie и kÎ[0, r–1] (рис. 2). Чтобы определить границы jm,0 и jm,r-1 этого отрезка, используем формулы (1)–(3). Сначала из равенства (3) найдем значения широт, соответствующих верхней и нижней границам рассматриваемого пиксела (ie, je) текстуры E: jtop=re(je+1), jbottom=re·je. Далее, подставляя их в формулу (1) и учитывая равенство (2), получим
Цвет пиксела (ie, je) текстуры E определим как среднее арифметическое цветов пикселов текстуры M, входящих в R:
Таким образом, рассмотрен следующий алгоритм преобразования текстуры из проекции Меркатора в эквидистантную цилиндрическую проекцию. · Определение области U (с индексами jeÎ[je,min, je,max]) текстуры E, на которую отображается текстура M. · Заполнение областей jeje,max черным цветом. · Для каждого пиксела (ie, je)ÎU: – определение соответствующего отрезка R из r пикселов текстуры M, – поиск границ R по формуле (4), – вычисление цвета пиксела (ie, je) по формуле (5). Создание текстуры маски Рассмотрим процедуру создания модифицированной текстуры T маски, необходимой для бесшовного добавления водных поверхностей, отсутствующих в подготовленной на предыдущем этапе текстуре E. Пусть T ' – исходная текстура маски в эквидистантной цилиндрической проекции. Белым цветом в ней отображается суша, а черным – водные поверхности. Для создания текстуры T необходимо осуществить размытие границ областей суши в пределах 0,0003–0,0005 % от большего из размеров текстуры T '. Чтобы береговая линия после слияния E и текстуры водной поверхности осталась четкой, размытие должно производиться непосредственно от границ белых областей в направлении черных. На рисунке 3 процесс размытия границ про- иллюстрирован на примере отдельного участка текстуры T '. Область размытия G для данного участка выделена пунктиром (рис. 3а). Половину данной области, прилежащую к суше, заполним серым цветом с числовым эквивалентом 0,5 (рис. 3б), после чего применим к G фильтр размытия по Гауссу. В результате использования фильтра получаем участок требуемой текстуры T (рис. 3в) – модифицированной маски.
Практическое использование описанных решений На базе предложенных в данной статье технологий и алгоритмов разработан программный комплекс, выполняющий синтез высокодетализированной текстуры земной поверхности (из набора тайлов в проекции Меркатора) для ее последующего использования при визуализации модели Земли в имитационно-тренажерных системах. Комплекс состоит из трех приложений: Map creator, Map converter, Map merger, работающих под управлением операционной системы Microsoft Windows, и одного сценария для программы Adobe Photoshop. Приложения ориентированы на решение подзадач, составляющих описанную технологию. Map creator отвечает за сборку текстуры высокого разрешения из набора тайлов формата BMP в несжатый RAW-файл, а также при необходимости за нарезку такой текстуры на тайлы (поддерживаются несколько форматов записи). Map converter обеспечивает преобразование текстуры в формате RAW из проекции Меркатора в эквидистантную цилиндрическую проекцию. Добавление водных поверхностей осуществляется с помощью Map merger. Сценарий, в свою очередь, обеспечивает возможность создания в Photoshop необходимой для Map merger текстуры маски. Данный п Таким образом, в данной статье предложены технология и алгоритмы создания высокодетализированной текстуры земной поверхности. Рассмотрены сборка текстуры из набора тайлов, преобразование текстуры с проекцией Меркатора в текстуру с эквидистантной цилиндрической проекцией, добавление отсутствующих в исходных данных водных поверхностей. На основе описанных подходов разработан программный комплекс из трех приложений и одного сценария для Adobe Photoshop, позволяющий готовить такую текстуру за несколько шагов. Литература 1. Тимохин П.Ю. Технология визуализации ландшафтов с использованием сверхбольших текстур // Гагаринские чтения: науч. тр. XXXIX Междунар. молодеж. науч. конф. М.: МАТИ, 2013. Т. 2. С. 130–131. 2. Osborne P. The Mercator projections, Edinburgh, 2013. URL: http://www.mercator99.webspace.virginmedia.com/mercator.pdf (дата обращения: 05.06.2013). 3. Evenden G.I. Libproj4: A Comprehensive Library of Cartographic Projection Functions. Falmouth, MA, USA, 2008. 4. Михайлюк М.В., Торгашев М.А. Система «GLView» визуализации для моделирующих комплексов и систем виртуальной реальности // Вестн. РАЕН. 2011. Т. 11. № 2. С. 20–28. References 1. Timokhin P.U. Tekhnologiya vizualizatsii landshaftov s ispolzovaniem sverkhbolshikh tekstur. Gagarinskie chteniya: Nauchnye trudy XXXIX Mezhdunar. molodezhnoy nauchnoy konf. [Gagarin readings: proc. of 39th youth scientific conf.]. Moscow, Russian State Technol. Univ. (MATI) Publ., 2013, vol. 2, pp. 130–131. 2. Osborne P. The Mercator projections. Edinburgh, 2008. Available at: http://www.mercator99.webspace.virginmedia.com/ mercator.pdf (accessed 5 June 2013). 3. Evenden G.I. Libproj4: A Comprehensive Library of Cartographic Projection Functions. Falmouth, MA, USA, 2008. 4. Mikhaylyuk M.V., Torgashev M.A. Visualisation system «GLView» for modeling complexes and virtual reality system. Vestnik RAEN [RANS bulletin]. 2011, vol. 11, no. 2, pp. 20–28.je,max черным цветом. · |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3658 |
Версия для печати Выпуск в формате PDF (7.95Мб) Скачать обложку в формате PDF (1.45Мб) |
| Статья опубликована в выпуске журнала № 4 за 2013 год. [ на стр. 55-60 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 На третьем этапе выполняется добавление водных поверхностей к подготовленной на первом этапе детализированной текстуре E с использованием маски T. При этом новый цвет E'i,j пиксела (i, j) текстуры E вычисляется по формуле
На третьем этапе выполняется добавление водных поверхностей к подготовленной на первом этапе детализированной текстуре E с использованием маски T. При этом новый цвет E'i,j пиксела (i, j) текстуры E вычисляется по формуле ,
,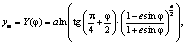 (1)
(1)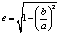 ; a и b – соответственно большая и малая полуоси земного эллипсоида (в рассматриваемой системе WGS84 a=6378137,0, b=6356752,3142).
; a и b – соответственно большая и малая полуоси земного эллипсоида (в рассматриваемой системе WGS84 a=6378137,0, b=6356752,3142).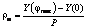 , где
, где 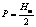 , jmax – географическая широта, соответствующая верхней строке пикселов (с координатой
, jmax – географическая широта, соответствующая верхней строке пикселов (с координатой 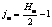 ) текстуры M (рис. 1а). Тогда, зная координату jm пиксела, легко найти для него ym, и наоборот:
) текстуры M (рис. 1а). Тогда, зная координату jm пиксела, легко найти для него ym, и наоборот: ,
,  , (2)
, (2)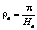 , тогда по значению широты φ можно вычислить координату jе :
, тогда по значению широты φ можно вычислить координату jе : . (3)
. (3) ,
, 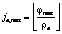 .
. ,
, 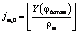 . (4)
. (4)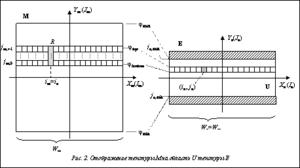
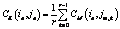 . (5)
. (5)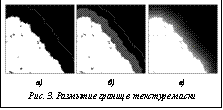 Указанные операции с текстурой удобно выполнять в графическом редакторе Adobe Photoshop, используя заранее подготовленный сценарий, описывающий необходимые действия.
Указанные операции с текстурой удобно выполнять в графическом редакторе Adobe Photoshop, используя заранее подготовленный сценарий, описывающий необходимые действия. рограммный комплекс апробирован при подготовке текстуры поверхности для модели Земли, разработанной в ЦВИСИТ НИИСИ РАН. На рисунке 4 представлено изображение, сгенерированное системой визуализации реального времени «GLView» [4], также созданной в ЦВИСИТ, в результате рендеринга моделей Земли и МКС.
рограммный комплекс апробирован при подготовке текстуры поверхности для модели Земли, разработанной в ЦВИСИТ НИИСИ РАН. На рисунке 4 представлено изображение, сгенерированное системой визуализации реального времени «GLView» [4], также созданной в ЦВИСИТ, в результате рендеринга моделей Земли и МКС.