Исследование функционирования центральной нервной системы, особенно головного мозга, направлено в первую очередь на выявление новых физиологически значимых эффектов на основе информации, содержащейся в электроэнцефалограммах (ЭЭГ), которые можно было бы связать с теми или иными формами психической активности человека. Поиск неизвестных, связанных с активностью головного мозга феноменов может осуществляться как в процессе разработки новых методов исследования (что в свое время, например, привело к появлению магнитно-резонансной и позитронно-эмиссионной томографии), так и путем создания новых методов анализа традиционных сигналов, посылаемых центральной нервной системой. К таким широко используемым методам относится электроэнцефалография, представляющая собой регистрацию электрической активности мозга с неповрежденных кожных покровов головы и являющаяся неинвазивным (то есть не требующим вживления электродов), относительно дешевым и малолатентным методом исследования, по праву занимающим одну из лидирующих позиций в системном анализе активности центральной нервной системы. Несмотря на существование многочисленных подходов к оценке данных ЭЭГ, имеющих широкие возможности как клинического, так и научного применения, целый ряд потенциально высокоинформативных способов по-прежнему используется недостаточно активно. В первую очередь речь идет о подходах к обработке данных ЭЭГ на основе вейвлет-анализа (ВА). Рост числа публикаций, в которых используются эти подходы, включая использование их результатов в ряде применяющихся в клинике программно-аппаратных комплексов (http://neurobotics.ru/ downloads/Neurobotics_Pricelist_2012.pdf), в большинстве случаев не ведет к созданию новых физиологически содержательных алгоритмов анализа данных ЭЭГ. Помимо этого, в ряде разработок ВА используется исключительно для фильтрации и сжатия данных без попыток провести интерпретацию полученных результатов в медико-биологическом аспекте.
Таким образом, актуальной является разработка таких методов, которые не только обеспечат обработку ЭЭГ на основе ВА, но и позволят провести физиологически значимую оценку результатов его применения. К таким методам относится предлагаемый в данной работе метод, основанный на анализе цепочек локальных максимумов (ЦЛМ) для матрицы коэффициентов вейвлет-преобразования. В его основу положены расчет и исследование поведения локальных максимумов в локальных спектрах (в матрице квадратов коэффициентов непрерывного вейвлет-преобразования) для относительно коротких (~ 0,1 с) отрезков времени. Полученные ЦЛМ (см. рис.) требуют, тем не менее, дальнейшей обработки с целью извлечения значимой информации о функционировании головного мозга человека или животных в различных состояниях.
 Целью настоящего исследования является разработка метода получения физиологически зна- чимой информации о работе головного мозга, основанного на анализе ЦЛМ, полученных в ходе обработки ЭЭГ человека в различных функциональных состояниях: покоя, решения в уме логических и образных задач. В основу метода положена парадигма, основанная на использовании идеологии выделения вызванных потенциалов головного мозга. Как известно [1], вызванные потенциалы представляют собой низкоамплитудные колебания электрического поля мозга, возникающие в ответ на определенные стимулы (вспышку света, резкий звук, щелчок, тактильное раздражение и т.п.) или предшествующие определенным действиям (например сокращению мышц) [2]. Поскольку амплитуда вызванных потенциалов значительно ниже амплитуд колебаний для фоновой ЭЭГ, в предлагаемом методе для улучшения отношения сигнал/шум используется когерентное накопление фрагментов ЭЭГ, связанных с изучаемым стимулом, что позволяет провести детальный анализ вызванных потенциалов.
Целью настоящего исследования является разработка метода получения физиологически зна- чимой информации о работе головного мозга, основанного на анализе ЦЛМ, полученных в ходе обработки ЭЭГ человека в различных функциональных состояниях: покоя, решения в уме логических и образных задач. В основу метода положена парадигма, основанная на использовании идеологии выделения вызванных потенциалов головного мозга. Как известно [1], вызванные потенциалы представляют собой низкоамплитудные колебания электрического поля мозга, возникающие в ответ на определенные стимулы (вспышку света, резкий звук, щелчок, тактильное раздражение и т.п.) или предшествующие определенным действиям (например сокращению мышц) [2]. Поскольку амплитуда вызванных потенциалов значительно ниже амплитуд колебаний для фоновой ЭЭГ, в предлагаемом методе для улучшения отношения сигнал/шум используется когерентное накопление фрагментов ЭЭГ, связанных с изучаемым стимулом, что позволяет провести детальный анализ вызванных потенциалов.
В ходе исследования проводится усреднение в частотно-временном пространстве частот локальных максимумов, присутствующих в данной ЦЛМ, для получения Ci, k – значений координат усредненной ЦЛМ i-го типа:
 , (1)
, (1)
где ai,j,k – значение частоты локального максимума; i=1, ..., 5 – тип ЦЛМ; j=1, ..., ni – номер цепочки в массиве ЦЛМ данного типа i (номера цепочек устанавливаются в соответствии с их длиной, меньший номер соответствует большей длине, общее количество цепочек типа i равно ni); k=1, ..., mi – номер точки в конкретной ЦЛМ типа i; mi – количество точек в наиболее длинной ЦЛМ i-го типа.
Важным моментом при использовании данного метода является выбор начальной точки для усреднения ЦЛМ как в частотном, так и во временном пространстве.
Для решения этой задачи во временном пространстве были использованы два подхода.
В первом из них усреднение выполняется после совмещения первых точек ЦЛМ, так что значения времени появления первых локальных максимумов ts1, ts2, ..., tsn будут равны нулю, где ts1 – время (или номер отсчета) появления первого локального максимума первой ЦЛМ; ts2 – время (или номер отсчета) появления первого локального максимума второй ЦЛМ при его наличии; tsn – время (или номер отсчета) появления первого локального максимума n-й цепочки, используемой в расчетах. Затем проводится синхронизация всех координат ЦЛМ во временном пространстве, заключающаяся в том, что рассчитываются средние значения частот для усредненной ЦЛМ. В случае отсутствия в одной из ЦЛМ точки с определенными временными координатами (на рисунке этот случай указан стрелкой) в общей суммации для данной временной координаты такая ЦЛМ не участвует. Следовательно, здесь усреднение осуществляется только по точкам, полученным в ходе расчета ЦЛМ, без учета искусственно построенных точек, например, в результате аппроксимации или интерполяции, которые могут заполнять участки ЦЛМ без локальных максимумов.
Во втором подходе используется функция Ui, характеризующая степень различия цепочек в частотном пространстве:
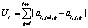 (2)
(2)
при l=1, 2, …, mi–ri; j=2, 3, …, ni; ri – число точек в текущей ЦЛМ i-го типа. Остальные обозначения те же, что и в формуле (1).
Требуется найти целое l, при котором значение функции Ui будет наименьшим. Минимум функции Ui будет указывать на такое взаиморасположение ЦЛМ во временном пространстве, при котором их различие в частотном пространстве будет минимальным. Таким образом, для получения итоговой усредненной ЦЛМ перед процессом усреднения каждая цепочка для j>1 сдвигается во временном пространстве на lj, где lj – значение l, соответствующее минимальному Ui для цепочки i-го типа с номером j.
Нетрудно заметить, что использование данного подхода, в котором ЦЛМ перед последующим усреднением выстраиваются, перемещаясь во временном пространстве путем изменения всех временных координат ЦЛМ за счет прибавления к ним константы l, позволяет минимизировать в частотном пространстве отличия данной ЦЛМ от ЦЛМ с максимальным числом локальных максимумов. При этом следует обратить внимание, что минимизация этих различий осуществляется именно с использованием шкалы значений, измеряемых в Гц, а не в масштабах вейвлет-преобразования, так как в этом случае данные, полученные для разных вейвлетов для одного и того же сигнала, могут существенно различаться. К тому же, используя именно частотное пространство и зная разрешение различных вейвлетов для определенных масштабов вейвлет-преобразования исследуемого сигнала, можно наиболее корректно интерпретировать классифицированные данные.
Однако реализация данных способов усреднения ЦЛМ в описанном выше виде сталкивается с рядом проблем. В частности, длина ЦЛМ, как во временном пространстве, так и характеризуемая числом точек, зависит от частоты (масштаба вейвлет-преобразования). Таким образом, суммация двух ЦЛМ, появившихся на ЭЭГ на частотах, например 3 и 35 Гц, представляется бессмысленной не только с физиологической точки зрения, но и с точки зрения численной обработки исследуемого сигнала. Для устранения данной проблемы применялось разделение на поддиапазоны всего исследуемого диапазона частот ЭЭГ: нижняя граница исследуемого поддиапазона бралась равной нижней границе θ-ритма, а верхняя – частоте Найквиста для данного электроэнцефалографа. Можно пользоваться таким разделением как в рамках классического варианта анализа ЭЭГ [3], так и путем построения поддиапазонов, исходя из динамических характеристик их границ, основанном на частотных значениях локальных минимумов, которые, подобно максимумам ЦЛМ, также изменяют свои частотные характеристики (способ исследования электроэнцефалограммы человека и животных защищен патентом № 2332160 в 2008 г., авторы: Я.А. Туровский, С.А. Запрягаев, С.Д. Кургалин).
Другая проблема, возникающая при получении усредненных ЦЛМ методом когерентного накопления, связана с их весьма различающейся динамикой поведения во времени.
Как видно из рисунка, можно выделить пять различных типов характера поведения ЦЛМ.
1. ЦЛМ со стабильно нарастающей частотой (область А на рисунке). Такие ЦЛМ во многом свойственны ЭЭГ в состоянии покоя. Характер увеличения частоты локального максимума для разных случаев здесь различен, что, возможно, позволит выделить несколько подтипов данного типа поведения ЦЛМ. Поведение ЦЛМ в частотном пространстве различается как по скорости ν дрейфа частот (ν=ω/t, где ω – частота; t – время; ν измеряется в Гц/с), так и по форме получившейся ЦЛМ в пространстве время – масштаб вейвлет-преобразования. Наблюдаются следующие виды динамики поведения ЦЛМ: а) линейно-равномерная (когда зависимость ν(t) хорошо аппроксимируется линейной функцией); б) неравномерная (когда тренды, построенные по началу и концу ЦЛМ, отличаются от ее центральной части).
2. ЦЛМ со стабильно убывающей частотой (область Б на рисунке). Как и для ЦЛМ первого типа, характер снижения частоты для ЦЛМ данного типа достаточно сильно различается. Возможно, стабильно убывающий тип представляет собой обратный по сравнению с первым типом вариант функционирования осцилляторов, модулирующих электрическую активность головного мозга, порождающих поведение ЦЛМ первого типа.
3. ЦЛМ без динамики изменения в частотном пространстве (область В на рисунке). Осциллятор (или группа осцилляторов) головного мозга не увеличивает и не уменьшает свою частоту в пределах разрешающей способности используемого вейвлета.
4. ЦЛМ, в которых сначала происходит рост частоты, а потом ее уменьшение, при том, что ЦЛМ может завершиться как на более высокой, так и на более низкой по сравнению с начальной частоте (область Г на рисунке).
5. ЦЛМ, демонстрирующие первоначальное уменьшение частоты с последующим ее ростом. Как и для ЦЛМ предыдущего типа, отношение частот начала и завершения ЦЛМ может быть различным (область Д на рисунке).
Проведенная выше типологизация локальных максимумов матриц вейвлет-коэффициентов для ЭЭГ имеет важное значение для исследования процессов ЭЭГ в различных функциональных состояниях человека.
С учетом и на основе представленной выше классификации различных типов характера поведения ЦЛМ авторами был разработан програм- мный модуль дополнительно к уже существующему программно-аппаратному комплексу ана- лиза ЭЭГ, включающему в себя два синхронно работающих электроэнцефалографа, компьютерный сервер и ряд вычислительных узлов, реализованных на технологии CUDA, обеспечивающих одновременное использование более 1 300 процессоров на видеокартах. Получены результаты, демонстрирующие изменение характера дрейфа элементов ЦЛМ в частотном пространстве и свидетельствующие о высокой чувствительности предлагаемого метода к различным состояниям головного мозга человека, зарегистрированным с помощью ЭЭГ. Разработаны индивидуальные карты динамики диапазонов, применяемых в анализе ЭЭГ для 19 испытуемых, которые проходили ряд тестов, связанных с решением логических и образных задач.
Разработанный метод, помимо его использования для анализа ЭЭГ, может быть применен для изучения различных биомедицинских сигналов: электрокардиографического, вариабельности сердечного ритма, суточного мониторинга арте- риального давления, лазерной допплеровской флоуметрии и др. Можно предположить, что его широкое использование позволит выявить новые закономерности и за пределами медико-биологических исследований.
Литература
1. Гнездицкий В.В. Вызванные потенциалы мозга в клинической практике. М.: МЕДпресс-информ, 2003. 264 с.
2. Психофизиология: учеб. для вузов; [под ред. Ю.И. Александрова]. СПб: Питер, 2012. 464 с.
3. Зенков Л.Р. Клиническая электроэнцефалография (с элементами эпилептологии). М.: МЕДпресс-информ, 2011. 356 с.
References
1. Gnezditskiy V.V. Vyzvannye potentsialy mozga v klinicheskoy praktike [Evoked brain potential in clinic practice]. Moscow, MEDpress-inform Publ., 2003, 264 p.
2. Aleksandrov Yu.I. Psikhofiziologiya: ycheb. dlya vuzov [Psychophysiology: students book]. St. Petersburg, Piter Publ., 2012, 464 p.
3. Zenkov L.R. Klinicheskaya elektroentsefalografiya (s elementami epileptologii) [Clinic electroencephalography (with elements of epileptology)]. Moscow, MEDpress-inform Publ., 2011, 356 p.




 , (1)
, (1)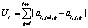 (2)
(2)