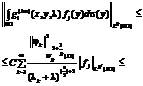Авторитетность издания
Добавить в закладки
Следующий номер на сайте
О некоторых обратных спектральных задачах для произвольного возмущения бигармонического оператора с сингулярными коэффициентами
Аннотация:Рассматривается классическая обратная граничная спектральная задача для произвольного возмущения бигармонического оператора с сингулярными коэффициентами из некоторых пространств Соболева. Задача формулируется следующим образом: определяют ли однозначно собственные значения задачи Дирихле и некоторые производные соответствующих нормированных собственных функций на границе гладкой ограниченной области коэффициенты этого оператора? Доказано (как первый шаг в решении этой проблемы), что собственные значения задачи Дирихле и производные до второго порядка нормированных собственных функций на границе однозначно определяют так называемое преобразование от Дирихле к Нейману, которое соответствует самосопряженному расширению по Фридрихсу произвольного возмущения бигармонического оператора с сингулярными коэффициентами. Главную роль в этом доказательстве играет существование функции Грина и ее оценки вплоть до границы области. Эти факты позволят нам доказать классическую теорему Борга-Левинсона для операторов четвертого порядка такого типа.
Abstract:The classical inverse boundary spectral problem for any perturbation of the bi -harmonic operator with singular coefficients from some Sobolev spaces is considered. The problem is formulated as follows: Do the Dirichlet eigenvalues and some derivatives of the corresponding normalized eigenfunctions at the boundary of smooth bounded domai n uniquely determine the coefficients of this operator? We proved the first step of this problem, i.e. we proved that the Dirichlet eigenvalues and the derivatives up to the second order of the normalized eigenfunctions at the boundary uniquely determine t he so-called Dirichlet-to-Neumann map that corresponds to the Friedrichs self-adjoint extension of any perturbation of the bi-harmonic operator with singular coefficients. The main role in this proof is played by the existence of the Green’s function and its estimates up to the boundary of the domain. These facts will allow us to prove the classical Borg-Levinson theorem for the operators of fourth order of such type.
| Авторы: Серов В.С. (vserov@cc.oulu.fi) - Университет прикладных наук Оулу (профессор ), Оулу, Финляндия, доктор физико-математических наук | |
| Ключевые слова: функции грина, расширение по фридрихсу, преобразование от дирихле к нейману |
|
| Keywords: green’s function, friedrichs extension, dirichlet-to-neumann map |
|
| Количество просмотров: 5675 |
Версия для печати Выпуск в формате PDF (6.10Мб) Скачать обложку в формате PDF (0.87Мб) |
The subject of this work concerns to the classical inverse spectral problem. This inverse problem can be formulated as follows: do the Dirichlet eigenvalues and the derivatives (which order?) of the normalized eigenfunctions at the boundary determine uniquely the coefficients of the corresponding differential operator? For operators of order two this type of theorem is called Borg-Levinson theorem. In the case of the Schrödinger operators the knowledge of the Dirichlet eigenvalues and the normal derivatives of the normalized eigenfunctions at the boundary uniquely determine unknown potential. Borg-Levinson theorem for the Schrödinger operators was proved for the first time by Nachman, Sylvester and Uhlmann [1] for the potentials from the space For the magnetic Schrödinger operator with singular coefficients Borg-Levinson theorem was proved for the first time by Serov [6]. The proof of this result for the magnetic Schrödinger operators uses the same technique as for the Schrödinger operators with singular potentials. It must be mentioned here that the magnetic Schrödinger operator cannot be considered as a "small" perturbation of the Schrödinger (or Laplace) operator. For the operator of order 4 which is the first order perturbation of the bi-harmonic operator with Navier boundary conditions on a smooth bounded domain in Rn, n³3, it is proved by Krupchyk, Lassas and Uhlmann [7] that the Dirichlet-to-Neumann map uniquely determine this first order perturbation. The main goal of present work is to show that the knowledge of the discrete Dirichlet spectrum and some special derivatives up to the second order of the normalized eigenfunctions at the boundary uniquely determine the Dirichlet-to-Neumann map that corresponds to an arbitrary perturbation of the bi-harmonic operator with singular coefficient from some Sobolev spaces on the smooth bounded domain in Rn, n³2. The next step might be to prove that the knowledge of the Dirichlet-to-Neumann map uniquely determines the coefficients of the operator H4 which is an arbitrary perturbation of the bi-harmonic operator. The solution of this problem will be given in future publications. Below we use the following notations. The space Wpt(W), t³0,1£p£¥, denotes the Lp – based Sobolev space in the domain W and the space Green’s function Let W be a bounded domain with smooth boundary in Rn, n³2. We consider in this domain the following operator of order four that we will call the "magnetic" operator of 4th order with variable coefficients
where Ñ denotes the gradient in Rn, D denotes the Laplacian in Rn and where the coefficients
and where it is assumed (WLG) that the value of p is the same for all these spaces. It is well-known that under the conditions (2) and (3) for the coefficients the following Gårding’s inequality holds (see, for instance, [9]):
where 00. This inequality allows us to define symmetric operator (1) by the method of quadratic forms. Then H4 has a self-adjoint Friedrichs extension denoted by (H4)F with domain
where
The spectrum of this extension is purely discrete, of finite multiplicity and has an accumulation point only at the +¥: l1£l2£…£lk£… ®+¥. The corresponding orthonormal eigenfunctions Therefore for any l ³ m0 the operator (H4)F+lI is positive and its inverse ((H4)F + lI)–1: L2(W) ® L2(W) (6) is compact. It is an integral operator with kernel denoted by G(x, y, l). If we use for this integral operator the symbol
Definition 1. The kernel G(x, y, l) of the integral operator Our first result is: Theorem 1. Suppose that
and where x, yÎW and constants C>0 and d>0 do not depend on x, yÎW and l. Proof. It is well-known that the fundamental solution of the operator D2+lI, l>0, has exactly these estimates (8)–(10). The conditions (2) and (3) for the coefficients that are in front of the derivatives of order one and higher of the operator H4 allow us to conclude that they belong to the Kato space Kn–1(Rn) (if we extend them by zero outside of the domain W), i.e.
Using this fact we can easily prove the existence of the fundamental solution for the operator H4+lI. Moreover, the same estimates (8)–(10) will be fulfilled for this fundamental solution too. In order to obtain the same estimates (8)–(10) for the Green’s function G(x, y, l) we refer to the paper [10] (with some changes that are connected to the operator of order 4). Theorem 1 is proved. We have three immediate corollaries of Theorem 1 (see again [10]). Corollary 1. Assume that
where l³m0 with m0 as in Theorem 1. Corollary 2. Assume that Corollary 3. Assume that
converges. Remark 1. It can be mentioned here that the estimates (8)–(10) of the Green’s function of the "magnetic" operator (1) are obtained in Theorem 1 for quite weak conditions of the coefficients of H4. As far as we know they never appeared in the literature. Dirichlet-to-Neumann map and eigenfunctions Lemma 1. Under the conditions (2) and (3) for the coefficients of H4 we have that for any two functions u and f from
L1u(x)=¶v(Du)(x)+i¶v( –F¶vu(x)–iv× and L2u(x)=–Du(x)–i respectively. Here v is unit outward normal vector at the boundary of the domain W. Proof. The proof of this lemma is straightforward and is based only on the divergence theorem ("integration by parts"). And the main purpose of this lemma is to define the map L=(L1, L2). It must be mentioned also here that the conditions (2) and (3) for the coefficients of the operator H4 and the conditions for the functions u and f from this lemma guarantee the existence of the traces of the corresponding terms in L1u(x), L1f(x), L2u(x) and L2f(x) on the boundary ¶W from some Besov spaces. This fact justifies the correct application of the integration by parts and proves this lemma. Let l³m0 with m0 as in Chapter 1. Consider the following Dirichlet problem: ((H4)F+lI)u(x)=0; xÎW, u(x)=f0(x), ¶vu(x)=f1(x), xζW, (14) where the boundary functions f0(x) and f1(x) satisfy the following conditions:
where Using the technique of the multipliers from Sobolev spaces (see, for example, [11]) it can be proved that there exists a unique solution of the Dirichlet boundary value problem (14)–(15) from the spaces
Thus, we may define the Dirichlet-to-Neumann map Ll. Definition 2. The Dirichlet-to-Neumann map Ll for Dirichlet boundary problem (14)–(15) is defined as the following two-dimensional vector
where v is outward normal vector at the boundary ¶W. Conditions (2), (3), (15) and (16) imply that the Dirichlet-to-Neumann map (17) acts as (for fixed l)
with p as in (15). The following theorem can be considered as one of the main results of this work. Theorem 2. Assume that
where Proof. Let w (x): =u1(x)–u2(x), where uj(x), j=1,2, solves the problem (14) with This problem can be rewritten in the domain W as
and with Dirichlet boundary conditions w(x)=0, ¶vw(x)=0, xζW. (21) Denote by (I + K)w(x)=F(x), (22) where the integral operator K and the function F are given by
and
We consider this equation (22) in the space of functions from the Sobolev space Due to the assumptions (2) and (3) for the coefficients
where constant C is independent on l³m0. Since p satisfies the inequality
This fact and the conditions (2) and (3) allow us to obtain from (24) and (25) that
We apply now the result from [12] and obtain that
By combining the inequalities (26) and (27) we get the following inequality
The interpolation of (26) and (28) leads us to the inequality
where 0£s£4. Using the definition (17) and the equalities for the terms
Using trace theorem and (29) we can estimate the latter terms as follows:
Since We are in the position now to estimate the normalized eigenfunctions of the magnetic Schrödinger operator. Lemma 2. Under the assumptions (2) and (3) for the coefficients
where 0£s£4, Proof. Let lk be an eigenvalue and jk(x) corresponding orthonormal eigenfunction. Then Corollary 2 from Theorem 1 allows us to obtain quite easily that
where 1£p£¥ and constant C>0 depends only on n, p and Vol(W). Rewriting the equation for the eigenfunctions jk(x) in the form (D2+m0I+Q(x, ¶))jk(x)=(lk+m0)jk(x), xÎW, jk(x)=0, ¶vjk(x)=0, xζW, where Q(x, ¶) is the rest of the operator H4, and applying the inequality (25), we obtain for any
Now by interpolation of (32) and (33) we obtain (31). Thus, Lemma 2 is proved. The next lemma shows us the representation for the kernel of the operator Ll. Lemma 3. For
where the kernels
and where for l³m0 the right-hand sides of (35) are converging in Lp(¶W´¶W). Proof. Solution u of the problem (14)–(15) definitely depends on l and we will denote it from now on as u(x, l) with l³m0. Integration by parts for the problem (14) with the boundary conditions f0 and f1 from (15) leads to
where G(x, y, l) is the Green’s function of (H4)F+lI defined in (6)–(10) and vy denotes the outward normal vector in y. In our case the Green’s function is given by
Since u solves the problem (14)–(15) then using J. von Neumann spectral theorem it can be easily proved by induction that
The operator ((H4)F + lI)–1 is well-defined by the spectral theorem and it is the integral operator with kernel denoted by Gl(x, y, l)
This fact allows us to represent ((H4)F+lI)–1u(x, l) as follows
where uk(l) is given by Integration by parts in the last equality gives us
Combining (39) and (40) we obtain the following equality ((H4)F+lI)–1u(x, l)=
which coincides for l=0 with (36). Since u solves the boundary value problem (15)–(16) using (17) we can obtain
Thus, the equalities (38), (41) and (42) give us that formally we have for the vector
and
Here we have used the following equalities for the eigenfunctions jk(x) at the boundary (see (15) and (31)): ¶vjk=0, ¶v(Djk)=D(¶vjk), xζW. The latter equalities show that this lemma will be proved if we show the convergence of all series (35) in Lp(¶W´¶W). To this end, the inequality (31) from Lemma 2, the conditions (2) and (3) for the coefficients and Sobolev imbedding theorem allow us to conclude that
By using these estimates and taking now
where From spectral data to Dirichlet-to-Neumann map Now we are in the position to formulate and to prove the second main result of this work. By symbol Theorem 3. Assume that
and
Then for all l³m0
for any Proof. The conditions (43) and (44), Lemma 3 (see formulas (34), (35)) imply that for all l³m0 and for
where two-dimensional vector-valued operators Remark 2. This theorem means that the inverse boundary spectral problem for the operator H4 is reduced to the problem of the reconstruction of the unknown coefficients of this operator by the knowledge of Dirichlet-to-Neumann map. Acknowledgments. This work was supported by the Academy of Finland (Application No. 250215, Finnish Programme for Centres of Excellence in Research 2012–2017). References 1. Nachman A., Sylvester J., Uhlmann G. An n-dimensional Borg-Levinson theorem. Comm. Math. Phys. 1988, vol. 115, pp. 595–605. 2. Novikov R.G. Multidimensional inverse spectral problem for the equation –Dy+(v(x)–Eu(x))y=0. Funct. Anal. Appl. 1988, vol. 22, pp. 263–272. 3. Päivärinta L., Serov V. An n-dimensional Borg-Levinson theorem for singular potentials. Adv. Appl. Math. 2002, vol. 29, pp. 509–520. 4. Kachalov A., Kurylev Ya., Lassas M. Inverse boundary spectral problems. Chapman Hall/CRC Publ., 2001. 5. Kurylev Ya., Lassas M., Weder R. Multidimensional Borg-Levinson theorem. Inverse Problems. 2005, vol. 21, pp. 1685–1696. 6. Serov V.S., Borg-Levinson theorem for magnetic Schrödinger operator. Bull. Greek Math. Soc. 2010, vol. 57, pp. 321–332. 7. Krupchyk K., Lassas M., Uhlmann G. Determining a first order perturbation of the bi-harmonic operator by partial boundary measurements. J. Funct. Anal., 2012, vol. 262, pp. 1781–1801. 8. Tanabe H. Functional analytic methods for partial differential equations. Dekker Publ., NY, 1997. 9. Hörmander L. The analysis of linear partial differential equations. Springer-Verlag Publ., NY, 1983, vols. 1–2. 10. Serov V. Green’s function and convergence of Fourier series for elliptic differential operators with potential from Kato space. Abstr. Appl. Anal., 2010, vol. 2010, 902638 (18 p.). 11. Mazja V.G., Shaposhnikova T.O. Theory of Sobolev multipliers with applications to differential and integral operators. Springer-Verlag Publ., Berlin, Heidelberg, 2009. 12. Triebel H. Theory of function spaces. Leipzig, Akademische Verlagsgechellchaft Geest and Portig K.-L. Publ., 1983. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3834 |
Версия для печати Выпуск в формате PDF (6.10Мб) Скачать обложку в формате PDF (0.87Мб) |
| Статья опубликована в выпуске журнала № 2 за 2014 год. [ на стр. 192-198 ] |
Назад, к списку статей



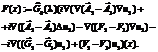 (24)
(24)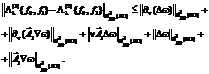
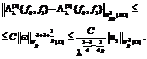 (30)
(30)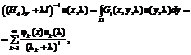 (39)
(39)