Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Линейное решение задачи квадратичного программирования
Аннотация:В работе описан метод поиска максимума квадрики на многогранном множестве ограничений, основанный на решениях систем линейных уравнений, размерность которых не выше числа переменных целевой функции. Вначале путем ортогональных преобразований и масштабирования матрица квадратичной формы приводится к нормальному виду. Затем с помощью замены переменных исходная задача сводится к задаче поиска минимального расстояния между точкой безусловного экстремума и многогранным множеством ограничений. Для определения расстояния строятся перпендикуляры к граням многогранника различной размерности. Для уменьшения числа исследуемых граней разработан специальный порядок перебора граней. Исследованию подлежат только грани, содержащие вершину, ближайшую к точке безусловного экстремума, и видимые из этой точки. В случае наличия нескольких ближайших равноудаленных вершин исследуется грань, содержащая все эти вершины, и грани меньшей размерности, имеющие с первой гранью не менее двух общих ближайших вершин.
Abstract:The work describes a quadric maximum search method on a polyhedral restrictions set. It is based on solving linear equations systems when their dimension no higher than a number of objective function variables. In the beginning, a quadric matrix is worked reduced to a normal view using orthogonal transformations and scaling. Then, using variables re-placement, the initial problem is reduced to a problem of searching the minimum distance between an unconditional extremum point and a polyhedral restrictions set. Perpendiculars to different dimension polyhedron sides are constructed to measure the distance. The special order of sides search is developed to reduce the number of studied sides. The subject to re-search includes only the sides containing the top which is the closest to an unconditional extremum point and seen from this point. If there is not only one closest top, then the side containing all these tops and the sides of lower dimension having not less than two shared closest tops with the first side are investigated.
| Авторы: Татаренко С.И. (srgiv@mail.ahp.tstu.ru) - Тамбовский государственный технический университет, Тамбов, Россия, кандидат технических наук | |
| Ключевые слова: квадратичная задача, нелинейное программирование, оптимизация, математическое программирование |
|
| Keywords: quadratic problem, non-linear programming, optimisation, mathematical programming |
|
| Количество просмотров: 13869 |
Версия для печати Выпуск в формате PDF (5.36Мб) Скачать обложку в формате PDF (1.03Мб) |
Для решения задачи квадратичного программирования разработаны различные приближенные методы и варианты квадратичного симплекс-метода, основанные на методе Лагранжа [1–4]. Но приближенные методы не способны дать точное решение, а симплекс-метод требует введения дополнительных переменных и учета нелинейных условий дополнительной нежесткости, что усложняет задачу и увеличивает ее размерность. В [5] описан метод, заключающийся в последовательном решении квадратичной задачи на различных гранях множества ограничений, при этом требуется решать системы линейных уравнений меньшей размерности, чем при использовании симплекс-метода, но большей, чем число переменных целевой функции. В данной работе предложен точный метод решения квадратичной задачи, основанный на решениях систем линейных уравнений, размерность которых не выше числа переменных целевой функции.
Суть метода состоит в том, что задача поиска максимума квадрики на многогранном множестве ограничений сводится к задаче поиска минимального расстояния между точкой безусловного максимума и границей многогранной области ограничений. Для определения расстояния строятся перпендикуляры к граням многогранника, а для уменьшения числа исследуемых граней разработан специальный порядок перебора граней. Пусть имеется задача квадратичного программирования с целевой функцией от n переменных и замкнутой областью ограничений из m линейных неравенств: z(X) = XTAX + BX ® max, (1) CX ³ D; X ³ 0, где X = (x1, x2, …, xn)T – вектор переменных; A – матрица квадратичной формы размерности n´n; B = (b1, b2, …, bn) – вектор линейной формы; D = (d1, d2, …, dm)T – вектор констант ограничений; C – матрица коэффициентов ограничений размерности m´n. Пусть матрица A невырождена, отрицательно определена и точка решения задачи безусловного максимума X* = – (A+AT)–1BT = –A–1BT /2 находится вне области ограничений. Тогда решение задачи (1) следует искать на границе области ограничений [6]. Первым этапом решения является масштабирование задачи, заключающееся в замене переменных и приведении матрицы квадратичной формы к нормальному виду. Сначала методом ортогональных преобразований [7, 8] приведем матрицу квадратичной формы A к каноническому виду. Обозначим матрицу этого преобразования S, тогда в результате преобразований матрица F = STAS станет диагональной, причем, по закону инерции квадратичной формы, все ее диагональные элементы будут отрицательны и равны собственным числам матрицы A. Затем приведем квадратичную форму к нормальному виду с помощью масштабирующей диагональной матрицы W: wi,j = в итоге матрица квадратичной формы превратится в отрицательную единичную матрицу WTSTASW= =–E, а алгебраическая форма целевой функции после замены переменных X=SWY примет вид z(Y)=å(–yi2+piyi)®max, iÎ[1, n], где P=BSW, Y= =W–1S–1X. Дополним каждую переменную до полного квадрата, заменим знак целевой функции, исключим из нее постоянные члены и получим задачу поиска минимума: z(Y) = å(yi – pi/2)2®min, iÎ[1, n ]. (2) Поскольку Y* = W–1S–1X*, матрица S ортогональна, то есть S–1 = ST, матрица W–1 диагональная и W–1 = (W–1)T, то W–1S–1A–1S–1W–1 = –E, следовательно, Y* = PT/2 Объединим ограничения неравенства с ограничениями неотрицательности переменных и получим систему из l=n+m ограничений: GY ³ Q, (3) где Таким образом, задача (1) превратилась в задачу (2), (3), представляющую собой задачу поиска точки границы многогранного множества U, описываемого неравенствами (3), ближайшей к точке безусловного экстремума Y* = PT/2. Вторым этапом решения является исследование элементов границы области U и отыскание ближайшей точки методами аналитической геометрии. Ограничения (3) образуют в n-мерном пространстве выпуклый многогранник (полиэдр), граница которого состоит из вершин и граней различных размерностей от 1 до n–1 [9]. Разделим ограничения задачи на две группы. В одну группу включим ограничения, которым удовлетворяет точка безусловного экстремума GiY* ³ qi, грани множества U размерности n–1, расположенные на соответствующих опорных гиперплоскостях, будут невидимыми из точки Y*. Здесь Gi – строка матрицы G; qi – элемент вектора констант ограничений Q. В другую группу включим ограничения, которым не удовлетворяет точка Y*, то есть для которых GiY* < qi, соответствующие грани будут видимыми из Y*. Найдем все видимые вершины многогранника U как решения всех возможных систем из n уравнений, образованных из ограничений (3) путем замены знака неравенства на равенство. В составе этих систем должно быть на менее одного ограничения из числа видимых n { GiY = qi ; i Î[1,l]; $i : GiY* < qi, где Gi – строка матрицы G; qi – элемент вектора констант ограничений Q. Решением такой системы будет вершина, если оно удовлетворяет всем ограничениям (3). Если некоторые из ограничений не выполняются, то найденная точка является пересечением продолжений гиперплоскостей граней и не принадлежит U. Вершина может быть общей точкой и для большего чем n числа гиперплоскостей, но для ее нахождения достаточно решить систему из n уравнений [9]. При формировании систем уравнений для нахождения вершин следует исключать из рассмотрения системы, содержащие параллельные гиперплоскости, соответствующие линейно зависимым коэффициентам ограничений Gi = aGj. Если определитель системы равен нулю, это свидетельствует об отсутствии общей точки у гиперплоскостей [10], такие системы также не следует рассматривать. Примером в трехмерном пространстве может служить бесконечно длинная треугольная призма, образованная тремя попарно пересекающимися плоскостями. Поскольку вершина может принадлежать более чем n гиперплоскостям, следует проверить каждую найденную вершину на принадлежность еще не рассмотренным гиперплоскостям ограничений и, если имеются гиперплоскости, содержащие эту вершину, исключить из рассмотрения соответствующие системы уравнений. После нахождения всех вершин многогранника выберем ту, которая ближе всех к точке безусловного экстремума Y*, и обозначим ее V. Найденная вершина является либо решением задачи (2), (3), либо вершиной, ближайшей к искомому решению, и принадлежит грани многогранника U, содержащей точку решения. Поэтому далее надо исследовать грани всех размерностей, содержащие вершину V. Исследование проводится путем опускания перпендикуляра из точки Y* на все грани, содержащие вершину V. Перпендикуляр, опущенный из точки Y* на грань размерности k, не может быть длиннее перпендикуляра, опущенного на грань размерности k–1, имеющей с гранью размерности k общие точки, поскольку грань размерности k–1 будет являться границей грани размерности k. Поэтому исследование начинается с граней размерности n–1, а затем исследуются грани меньшей размерности. Как только будет найдена точка, удовлетворяющая всем ограничениям (3) и лежащая на перпендикуляре, опущенном на грань из точки Y*, она и будет являться решением задачи. Если после исследования всех граней такая точка не будет найдена, решением является вершина V. Грань размерности n–1 описывается одним уравнением из ограничений (3). Проверять следует только грани, содержащие вершину V, то есть нужно исследовать только те видимые ограничения (3), которые входили в систему уравнений, используемую для нахождения V, и являются активными для точки V. Согласно [10], расстояние до грани определяется выражением r=(GiY*– qi)/ |Gi|; iÎ[1, l]: GiV = =qi, GiY* < qi . Если это расстояние больше разности между ближайшей вершиной и точкой безусловного экстремума r > |Y*–V|, дальнейшее исследование грани не выполняется. Если r = |Y*–V|, решением задачи является вершина V. Если r < |Y*–V|, необходимо найти координаты ближайшей к Y* точки гиперплоскости, содержащей грань. Они определяются с помощью нормального к гиперплоскости вектора T = (t1, t2, …, tn): ti = gi,j /|Gi|; iÎ[1, l]; jÎ[1, n]; и совместного решения канонического уравнения прямой, проходящей через точку Y*, и общего уравнения гиперплоскости ограничения: (y1–y*1) / t1 = (y2–y*2) / t2 =…= (yn – y*n) / tn; GiY=qi. Если решение этой системы удовлетворяет всем оставшимся l–1 ограничениям, то именно она является решением задачи (2), (3), если нет, то перпендикуляр из точки Y* на гиперплоскость не попадает на границу множества U и требуется исследовать другие грани или грани меньшей размерности. Последними исследуются ребра многогранника U, то есть прямые линии, образованные пересечением n–1 ограничений, причем хотя бы одно из ограничений должно быть видимым. Система уравнений n–1 {GiY = qi; iÎ[1, l]; $i : GiY* ³ qi; "i : GiV = qi является общим уравнением прямой линии в n-мерном пространстве. Направляющий вектор T=(t1, t2, …, tn) линии ребра можно найти из условий ортогональности его ко всем нормальным векторам плоскостей ограничений, образующих ребро, то есть равенства нулю n–1 скалярных произведений: n–1 {GiT = 0; iÎ[1, l]. Для решения этой системы одну из координат вектора T можно задать произвольно. Поскольку вершина V=(v1, v2, …, vn) принадлежит исследуемому ребру, координаты точки пересечения линии ребра и перпендикуляра к ребру, опущенному из точки Y*, определяются из системы уравнений, включающей канонические уравнения линии ребра, проходящей через точку V, и уравнения n–1-мерной плоскости с нормальным вектором T, содержащей точку Y*: (y1 – v1) / t1 =(y2 – v2) / t2 = … = (yn – vn) / tn; T(Y–Y*) = 0. Если решение этой системы удовлетворяет всем ограничениям (3), оно является решением задачи (2), (3); если удовлетворены не все ограничения, перпендикуляр к ребру попадает на продолжение линии ребра и следует исследовать другие ребра. Грани размерности от k=n–2 до k=2 исследуются с помощью дополнительных ортогональных гиперплоскостей размерности от n–1 до n–k+1. Гиперплоскость размерности n–k является совместным решением k уравнений из системы ограничений (3), причем, как и для грани размерности n–1, ограничения должны быть активными для V и хотя бы одно должно быть из числа видимых из Y*: k {GiY=qi; iÎ[1, l]; $i : GiY* Точка V принадлежит исследуемой грани, найдем еще n–2 точек, принадлежащих грани Y1, Y2, …, Yn–2, как независимые решения системы, определяющей грань, причем n–k компонентов решений задаются произвольно. Найдем нормальный вектор Tn–1 некоторой гиперплоскости размерности n–1, содержащей n–1 точек, принадлежащих исследуемой грани V, Y1, Y2, …, Yn–2, и проходящей через точку Y*: VTn–1 =0; Y1Tn–1 = 0; … Yn–2Tn–1 = 0; Y*Tn–1 = 0. Найдем далее нормальный вектор Tn–2 гипер- плоскости размерности n–2, проходящей через n–2 точек, принадлежащих исследуемой грани V, Y1, Y2, …, Yn–3, через точку Y* и ортогональный к вектору Tn–1: VTn–2 = 0; Y1Tn–2 = 0; … Yn–3Tn–2 = 0; Y*Tn–2 = 0; Tn–2Tn–1 = 0. Аналогично находятся остальные нормальные векторы для гиперплоскостей размерности n–3, n–4, n–k+1; для вектора гиперплоскости размерности n–i получим систему VTn–i = 0; Y1Tn–i = 0; … Yn–i+1Tn–i = 0; Y*Tn–i = 0; Tn–iTn–1 = 0 … Tn–iTn–i+1 = 0. Нормальный вектор Tn–k исследуемой грани размерности n–k должен быть ортогонален k пересекающимся прямым, принадлежащим этой грани, и ортогонален всем найденным ранее нормальным векторам гиперплоскостей большей размерности, содержащих исследуемую грань. В качестве пересекающихся прямых возьмем разности (V–Y1), (V–Y2), …, (V–Yk) и получим систему (V–Y1)Tn–k = 0; (V–Y2)Tn–k = 0; … (V–Yk)Tn–k = 0; Tn–k+1Tn–k = 0; Tn–1Tn–k = 0. Координаты ближайшей к Y* точки гиперплоскости размерности n–k определяются из канонического уравнения линии с направляющим вектором Tn–k, проходящей через точку Y*, и общего уравнения плоскости, проходящей через точку V, с нормальным вектором Tn–k: (y1–y*1) / t1n–k=(y2–y*2) / t2 n–k =…=(yn–y*n) / tn n–k; Tn-k(Y–V) = 0. Если решение этой системы удовлетворяет всем ограничениям (3), то оно является решением задачи (2), (3), если нет, то требуется исследовать другие грани. В некоторых случаях может получиться, что ближайших равноудаленных от Y* вершин несколько, тогда решение задачи (2), (3) является линейной комбинацией таких вершин и принадлежит грани, содержащей все эти вершины, либо границе этой грани, то есть грани меньшей размерности, причем содержащей не менее двух равноудаленных вершин. Пусть имеется k ближайших равноудаленных вершин, обозначим их как V1, V2, …, Vk, гиперплоскость ограничений с номером i содержит все равноудаленные вершины, если " j = [1, k] : GiVj = qi. Пусть таких гиперплоскостей v, тогда размерность грани, содержащей решение, будет n–v и гиперплоскость размерности n–v, содержащая ближайшую к Y*, будет описываться системой из v уравнений. Для нахождения решения следует опустить перпендикуляр на эту грань из точки Y*, как описано выше, причем при построении промежуточных ортогональных векторов вместо точек Y1, Y2, …, Yk следует использовать вершины V1, V2, …, Vk. Если точка пересечения перпендикуляра и грани удовлетворяет всем ограничениям (3), то она является решением задачи. Если удовлетворены не все ограничения, надо исследовать грани меньшей размерности n–v–1, имеющие с исследуемой гранью не менее двух общих ближайших вершин, затем грани размерности n–v–2 и так до граней размерности 1, то есть ребер. Полученные таким образом ребра обязательно будут содержать две ближайшие вершины, и ближайшей к Y* точкой ребра будет являться среднеарифметическое этих вершин Y = (Vi + Vj) /2. В отличие от случая с одной ближайшей вершиной, когда исследования прекращают, если точка перпендикуляра, опущенного на грань из Y*, удовлетворяет всем ограничениям (3), при нескольких ближайших вершинах следует продолжать исследование всех граней размерности n–v–1 и меньше и в качестве решения принимать точку грани, ближайшей к Y*. Предложенный алгоритм реализован в форме программы на языке С++. Вычислительные эксперименты на модельных примерах показали эффективность метода и возможность его применения для решения задач оптимизации. В частности, для решения задачи с целевой функцией от 3 переменных и областью ограничений, имеющей форму восьмигранной пирамиды, образованной пересечением 9 ограничений, для определения вершин потребовалось решить 25 систем из 3 уравнений, а для проведения перпендикуляров к граням и ребрам необходимо решить 12 систем из 3 уравнений и 7 систем из 2 уравнений. При решении этой задачи симплексным методом потребуется неоднократно решать систему из 12 уравнений с 24 неизвестными, чтобы выполнить 12 нелинейных условий дополняющей нежесткости. Литература 1. Леонов А.А., Жолобов Д.А. Расширение симплекс-метода для решения задач квадратичного программирования // Науч. сессия МИФИ-2004. М.: МИФИ, 2004. Т. 13. С. 82–83. 2. Климова Е.Н., Шур В.Л., Москалец О.В. Математическое моделирование оптимального портфеля ценных бумаг с ограничениями на отдельные активы // Вестн. СамГУ: Естественнонаучная сер. Самара, 2008. № 8/2 (67). С. 263–275. 3. Даугавет В.А. Численные методы квадратичного программирования. СПб: Изд-во СПбГУ, 2004. 127 с. 4. Куцый Н.Н., Осипова Е.А. Проблема начального допустимого базиса при решении задач линейного программирования // Вестн. ТГТУ. Тамбов, 2010. Т. 16. № 4. С. 780–788. 5. Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983. 384 с. 6. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. М.: Физматлит, 2011. 384 с. 7. Ильин В.А., Позняк Э.Г. Линейная алгебра: учеб. для вузов. М.: Физматлит, 2010. 277 c. 8. Новиков М.А. О приведении матриц квадратичных форм к взаимно упрощенным // Современные технологии. Системный анализ. Моделирование. 2010. № 2 (26). С. 181–187. 9. Циглер Г.М. Теория многогранников. М.: Изд-во МЦНМО, 2014. 568 с. 10. Розендорн Э.Р., Ефимов Н.В. Линейная алгебра и многомерная геометрия: учебник. М.: Физматлит, 2005. 464 с. References 1. Leonov A.A., Zholobov D.A. Simplex-method extention to solve quadratic programming problems. Nauchnaya sessiya MIFI-2004 [MEPhI-2014 scientific session]. Moscow, National Research Nuclear Univ. “MEPhI” Publ., 2004, vol. 13, pp. 82–83 (in Russ.). 2. Klimova E.N., Shur V.L., Moskalets O.V. Mathematical modeling optimal securities holdings with separate assets restrictions. Vestnik Samarskogo gos. universiteta. Estestvennonauchnaya seriya (Vestnik of Samara State Univ. Natural Science series). Samara, 2008, no. 8/2 (67), pp. 263–275 (in Russ.). 3. Daugavet V.A. Chislennye metody kvadratichnogo programmirovaniya [Numerical methods in quadratic programming]. St. Petersburg, 2004, 127 p. 4. Kutsy N.N., Osipova E.A. Initial admissible basis problem when solving nonlinear programming exercises. Vestnik Tambovskogo gos. tekhn. universiteta [Herald of Tambov State Technical University]. Tambov, 2010, vol. 16, no. 4, pp. 780–788 (in Russ.). 5. Polyak B.T. Vvedenie v optimizatsiyu [Introduction to optimization]. Moscow, Nauka Publ., 1983, 384 p. 6. Sukharev A.G., Timokhov A.V., Fedorov V.V. Kurs metodov optimizatsii [Course of optimization methods]. Moscow, Fizmatlit Publ., 2011, 509 p. 7. Ilyin V.A., Poznyak E.G. Lineynaya algebra [Linear algebra]. Moscow, Fizmatlit Publ., 2010, 277 p. 8. Novikov M.A. On quadratic forms matrix reduction to relatively simplified. Sovremennye tekhnologii. Sistemny analiz. Modelirovanie [Modern technologies. System analysis. Modeling]. Irkutsk, 2010, no. 2 (26), pp. 181–187 (in Russ.). 9. Ziegler G.M. Teoriya mnogogrannikov [Polyhedron theory]. Moscow, 2014, 568 p. 10. Rozendorn E.R., Efimov N.V. Lineynaya algebra i mnogomernaya geometriya [Linear algebra and multidimensional geometry]. Textbook, Moscow, Fizmatlit Publ., 2005, 464 p. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3856 |
Версия для печати Выпуск в формате PDF (5.36Мб) Скачать обложку в формате PDF (1.03Мб) |
| Статья опубликована в выпуске журнала № 3 за 2014 год. [ на стр. 36-40 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Поиск решения задачи целочисленного программирования с помощью итеративного округления координат
- Программный комплекс для расчета процесса нанесения покрытия в псевдоожиженном слое
- Теоретический подход к управлению социально-техническими системами
- Репрезентативность метрик на основе событий процессора Intel Sandy Bridge при анализе времени обработки данных в памяти
- Применение алгоритма перебора деревьев и метода имитации отжига для схемно-структурной оптимизации тепловых сетей
Назад, к списку статей



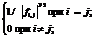
 и полученная целевая функция представляет собой квадрат расстояния между текущей точкой Y и точкой безусловного экстремума Y*, а поверхности равного уровня являются концентрическими гиперсферами с центром в точке Y*.
и полученная целевая функция представляет собой квадрат расстояния между текущей точкой Y и точкой безусловного экстремума Y*, а поверхности равного уровня являются концентрическими гиперсферами с центром в точке Y*. .
.