Рост автомобилизации в городах в последние десятилетия значительно опережает развитие улично-дорожных сетей. Эта проблема особенно характерна для крупных городов с исторической застройкой, где сложно, а часто и невозможно расширить проезжую часть. В связи с этим увеличивается значение эффективных методов управления транспортными и пешеходными потоками на существующей дорожной сети. Кроме того, проведение масштабных натурных экспериментов при управлении транспортными и пешеходными потоками невозможно [1–3], что обусловливает актуальность применения методов математического моделирования в этой области.
 Применяемые в настоящее время методы жесткого регулирования транспортных и пешеходных потоков предусматривают фиксированную длительность сигналов светофорного регулирования, рассчитанную с некоторым запасом на случай увеличения интенсивности движения. Такой подход в современных условиях все менее соответ- ствует динамично меняющимся параметрам транспортных и пешеходных потоков, увеличивая вероятность появления заторовых ситуаций. Регулирование пешеходных потоков при помощи светофоров вызывного действия вне пересечений является одним из аспектов задачи управления дорожным движением [2, 4]. Цикл работы такого устройства показан на рисунке 1.
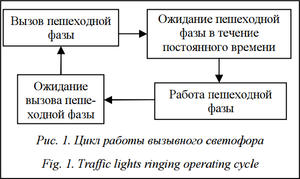
Применяемые в настоящее время методы жесткого регулирования транспортных и пешеходных потоков предусматривают фиксированную длительность сигналов светофорного регулирования, рассчитанную с некоторым запасом на случай увеличения интенсивности движения. Такой подход в современных условиях все менее соответ- ствует динамично меняющимся параметрам транспортных и пешеходных потоков, увеличивая вероятность появления заторовых ситуаций. Регулирование пешеходных потоков при помощи светофоров вызывного действия вне пересечений является одним из аспектов задачи управления дорожным движением [2, 4]. Цикл работы такого устройства показан на рисунке 1.
После вызова пешеходом своей фазы проходит некоторое заранее заданное время, после чего включается разрешающий сигнал для пешехода и запрещающий для автомобилей. В настоящее время большинство пешеходных светофоров используют постоянные значения времени ожидания пешеходной фазы, что в условиях интенсивного трафика, характерного для пиковой нагрузки дорожной сети, часто приводит к заторовой ситуации. На это влияют два фактора, которые становятся значимыми именно в часы пиковой нагрузки.
Первым фактором является значительное увеличение количества пешеходов на переходе в определенные часы. Это вызвано перемещением людей к местам работы в утренние часы и к местам проживания в вечерние часы. Вызывные пешеходные переходы обычно устанавливаются в местах, рассчитанных на небольшое количество пешеходов. Тем не менее, постоянное увеличение темпов строительства жилья и промышленных объектов меняет ситуацию, и нагрузка на эти переходы резко возрастает в указанные периоды. Постоянный поток пешеходов через переход в часы пиковой нагрузки приводит к тому, что пешеходная фаза вызывается ими постоянно и вызывной светофор начинает работать как регулярный. При этом время ожидания пешеходной фазы, как правило, не рассчитано на пиковую интенсивность движения в этом месте, значит, действие сигнала, запрещающего движение автомобилям, становится регулярным. Время этого действия равно времени ожидания пешеходной фазы вызывного светофора.
Вторым фактором, приводящим к заторовой ситуации на пешеходном переходе, является значительное увеличение интенсивности транспортного потока в те же пиковые часы. Обычно время ожидания пешеходной фазы вызывного пешеходного светофора устанавливается без учета того, что светофор будет работать в режиме постоянного вызова пешеходной фазы. В условиях значительного увеличения пешеходного потока это приводит к образованию очереди транспортных средств. Совпадение данного процесса во времени с действием первого фактора приводит к тому, что транспорт скапливается перед пешеходным переходом за время действия запрещающего сигнала и не успевает разъехаться за время ожидания. В результате происходит лавинообразное нарастание очереди и образование такого затора, у которого нет возможности разъехаться, так как время ожидания пешеходной фазы задано постоянным.
 При достижении пиковых значений интенсивности движения транспорта одновременное действие обоих вышеописанных факторов вызывает постоянное увеличение очереди автомобилей на пешеходном переходе. Эта очередь не успевает разъехаться за время действия разрешающего сигнала, который равен времени ожидания следующей пешеходной фазы, то есть обычно менее 30 секунд. Учет влияния этих двух факторов позволит привести заторовую ситуацию в норму и уменьшить возможность ее появления. Распространенной тенденцией решения данной задачи является применение светофорного регулирования с гибкой сменой длительности фаз [2, 3].
При достижении пиковых значений интенсивности движения транспорта одновременное действие обоих вышеописанных факторов вызывает постоянное увеличение очереди автомобилей на пешеходном переходе. Эта очередь не успевает разъехаться за время действия разрешающего сигнала, который равен времени ожидания следующей пешеходной фазы, то есть обычно менее 30 секунд. Учет влияния этих двух факторов позволит привести заторовую ситуацию в норму и уменьшить возможность ее появления. Распространенной тенденцией решения данной задачи является применение светофорного регулирования с гибкой сменой длительности фаз [2, 3].
Существующий нечеткий алгоритм регулирования пешеходного пересечения [5] предусматривает использование в качестве выходной переменной решения о прекращении или продлении разрешающего автомобильного сигнала, а в качестве входных – суммарное время ожидания пешеходами, количество машин между двумя детекторами на расстоянии 60 м, а также среднее расстояние между следующими друг за другом автомобилями. При разработке этого нечеткого алгоритма управления сигналом пешеходного перехода [5] было установлено, что он увеличивает производительность по сравнению с использованием фиксированного сигнала. В этом алгоритме используются 18 нечетких правил, что вдвое больше, чем при применении алгоритма, предлагаемого в настоящей работе.
С целью предупреждения заторовой ситуации предлагается определять время ожидания разрешающего сигнала пешеходного перехода в зависимости от двух величин: времени, прошедшего с последнего пешеходного перехода, и размера очереди транспортных средств, скопившихся перед переходом за это время. Если пешеходы осуществляли переход недавно, а размер очереди транспортных средств велик, то с целью предупреждения или стимулирования разъезда этой очереди нужно увеличить время ожидания пешеходной фазы. Если же, наоборот, времени с последнего перехода прошло много, а транспортных средств скопилось немного, время ожидания следует уменьшить с целью скорейшего пропуска пешеходов. При этом каждому сочетанию значений времени с последнего перехода и размера очереди следует сопоставить определенное значение времени ожидания следующей пешеходной фазы.
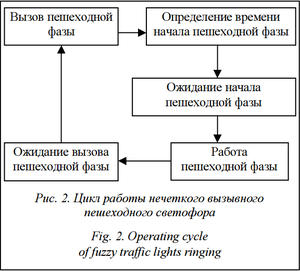
При использовании такой модели цикла работы вызывного светофора (рис. 2) даже уже образовавшийся затор имеет возможность разъехаться в течение конечного числа циклов регулирования. Размер очереди транспортных средств можно определять при помощи детекторов транспорта, например, на основе камер видеонаблюдения, совместно с выполнением ими других функций. Оценку времени, прошедшего с последней пешеходной фазы, и размера скопившейся перед переходом очереди транспортных средств, а также принятие решения о времени ожидания пешеходной фазы и времени ее действия можно проводить при помощи математического аппарата нечеткой логики [6–8].
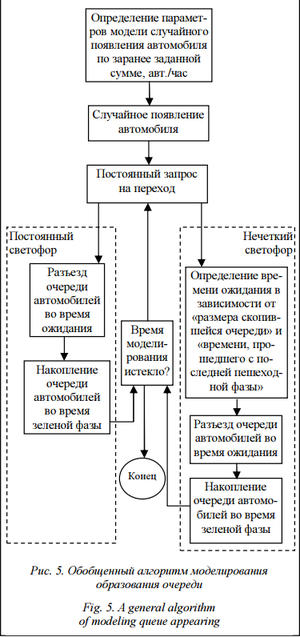
Такой подход к управлению пешеходными потоками на переходе в часы пиковой нагрузки [9, 10] позволит снизить возможность заторовой ситуации, а в случае ее возникновения привести ситуацию в норму в течение нескольких циклов регулирования. На основании цикла (рис. 2) предлагается алгоритм работы вызывного пешеходного светофора с нечетким управлением (рис. 3).
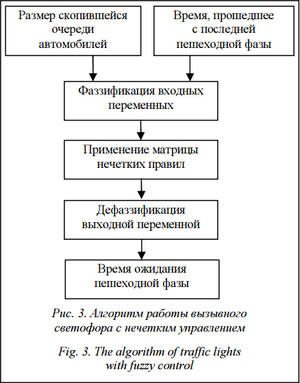 В качестве входных нечетких переменных определим время Tp, прошедшее с последнего вызова пешеходной фазы, и размер Nq очереди автомобилей, скопившихся перед пешеходным переходом за время действия предыдущей пешеходной фазы. Выходной нечеткой переменной является время W ожидания вызванной пешеходной фазы. Терм-множества входных переменных ограничим тремя значениями: малое, среднее, большое [7]. Для задания областей значений термов воспользуемся способом опроса экспертов (табл. 1).
В качестве входных нечетких переменных определим время Tp, прошедшее с последнего вызова пешеходной фазы, и размер Nq очереди автомобилей, скопившихся перед пешеходным переходом за время действия предыдущей пешеходной фазы. Выходной нечеткой переменной является время W ожидания вызванной пешеходной фазы. Терм-множества входных переменных ограничим тремя значениями: малое, среднее, большое [7]. Для задания областей значений термов воспользуемся способом опроса экспертов (табл. 1).
Определим (способом опроса экспертов) функции принадлежности входных переменных (табл. 1).
Таблица 1
Функции принадлежности входных переменных
Table 1
Membership functions of input variables
|
Значение терм-множества
|
Число машин, Nq, шт.
|
Время, прошедшее с последней пешеходной фазы, Tp, сек.
|
|
Малое
|
0–7
|
1–7
|
|
Среднее
|
7–20
|
7–15
|
|
Большое
|
15 и более
|
30 и более
|
При задании областей значений терм-множества выходной переменной целесообразно ограничиться пятью термами (табл. 2).
Значения нечеткой выходной величины W определяются в зависимости от сочетания Nq и Tp (табл. 3). На пересечениях строк и столбцов находятся значения выходной переменной (из табл. 2).
Таблица 2
Функция принадлежности выходной переменной
Table 2
A membership function of an output variable
|
Значение терм-множества
|
Время ожидания пешеходной фазы, сек.
|
|
Очень малое
|
0
|
|
Малое
|
10
|
|
Среднее
|
15
|
|
Большое
|
20
|
|
Очень большое
|
30
|
Таблица 3
Правила определения значения выходной величины
Table 3
The rules for determination of an output variable
|
Время, прошедшее с последней пешеходной фазы, Tp
|
Число машин
|
|
Малое
|
Среднее
|
Большое
|
|
Малое
|
Среднее
|
Большое
|
Очень большое
|
|
Среднее
|
Малое
|
Среднее
|
Большое
|
|
Большое
|
Очень малое
|
Малое
|
Среднее
|
Используя таблицу 3, определим список нечетких правил для определения выходной переменной.
Если Tp = малое, Nq = малое, то W = среднее.
Если Tp = малое, Nq = среднее, то W = большое.
Если Tp = малое, Nq = большое, то W = очень большое.
Если Tp = среднее, Nq = малое, то W = малое.
Если Tp = среднее, Nq = среднее, то W = среднее.
Если Tp = среднее, Nq = большое, то W = большое.
Если Tp = большое, Nq = малое, то W = очень малое.
Если Tp = большое, Nq = среднее, то W = малое.
Если Tp = большое, Nq = большое, то W = среднее.
Используя эти правила, проведем моделирование процесса накопления очереди транспортных средств на пешеходном переходе, расположенном вне пересечения, в условиях пиковой транспортной и пешеходной нагрузки. Для управления потоками транспорта и пешеходов используется вызывной светофор. Будем считать, что поток пешеходов непрерывен и запросы на переход следуют постоянно. Моделирование будем проводить для двух способов регулирования перехода (рис. 4).
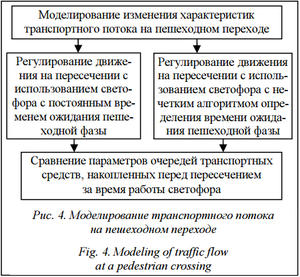 Первый способ – управление переходом при помощи вызывного светофора с постоянным временем ожидания фазы. Цикл работы такого светофора показан на рисунке 1. При втором способе используем вызывной светофор со временем ожидания фазы, определяемым при помощи нечетких правил, согласно алгоритму на рисунке 3. Цикл работы этого светофора показан на рисунке 2.
Первый способ – управление переходом при помощи вызывного светофора с постоянным временем ожидания фазы. Цикл работы такого светофора показан на рисунке 1. При втором способе используем вызывной светофор со временем ожидания фазы, определяемым при помощи нечетких правил, согласно алгоритму на рисунке 3. Цикл работы этого светофора показан на рисунке 2.
Результаты моделирования накопления очереди в течение определенного времени сравним по средней и максимальной длине очереди авто- мобилей перед пешеходным переходом. Обобщенный алгоритм моделирования накопления и разъезда очереди автомобилей перед переходом (рис. 5) предполагает случайное прибытие автомобилей к переходу с постоянным средним значением автомобилей в час, постоянную среднюю скорость разъезда очереди и постоянный запрос перехода пешеходами.
Моделирование было проведено в среде Matlab 7.0. Запросы на пешеходный переход следовали регулярно каждые 30 секунд, что характерно для пиковой нагрузки. Поток автомобилей установлен случайным в рамках заданной интенсивности (авт./час), средняя скорость разъезда – 1 авт./сек. Время ожидания разрешающего пешеходного сигнала в случае использования вызывного светофора с постоянным временем ожидания – 10 сек. Время запрещающего такта для автомобилей, равное времени перехода пешеходами, – 17 сек. (четырехполосная проезжая часть). Результаты для времени моделирования 250 сек. приведены в таблице 4 и на рисунке 6, для времени 10 часов – в таблице 5 и на рисунке 7. Интенсивность движения 1 600 авт./час и 2 100 авт./час.
Таблица 4
Результаты для времени моделирования 6 минут
Table 4
The results of modeling for 6 minutes
|
Транспортный поток, авт./час
|
Тип управления светофором
|
Средняя длина очереди, авт.
|
Максимальная длина очереди, авт.
|
|
1 600
|
Постоянный
|
2,9
|
8
|
|
Нечеткий
|
1,6
|
8
|
|
2 100
|
Постоянный
|
13,05
|
20
|
|
Нечеткий
|
2,12
|
9
|
Таблица 5
Результаты для времени моделирования 10 часов
Table 5
The results of modeling for 10 hours
|
Транспортный поток, авт./час
|
Тип управления светофором
|
Средняя длина очереди, авт.
|
Максимальная длина очереди, авт.
|
|
1 600
|
Постоянный
|
2,3
|
11
|
|
Нечеткий
|
0,75
|
6
|
|
2 100
|
Постоянный
|
275
|
600
|
|
Нечеткий
|
1,1
|
11
|
На рисунках 5 и 6 пунктирной ломаной линией показано накопление очереди при постоянном времени работы светофора, сплошной – динамика очереди при нечетком регулировании.
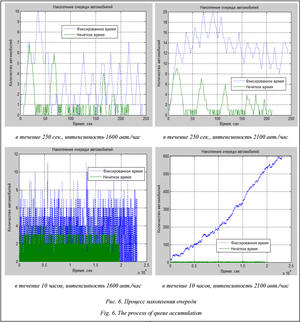 Как видно из результатов (табл. 4 и 5, рис. 6), нечеткий подход к управлению вызывным пешеходным светофором уменьшает среднюю длину очереди и возможность заторовой ситуации, а при ее возникновении прекращает ее за конечное число циклов работы.
Как видно из результатов (табл. 4 и 5, рис. 6), нечеткий подход к управлению вызывным пешеходным светофором уменьшает среднюю длину очереди и возможность заторовой ситуации, а при ее возникновении прекращает ее за конечное число циклов работы.
Литература
1. Кременец Ю.А., Печерский М.П., Афанасьев М.Б. Технические средства организации дорожного движения: учебник для вузов. М.: Академкнига, 2005. 279 с.
2. Иносэ X., Хакамада Т. Управление дорожным движением; [пер. с англ. Под ред. М.Я. Блинкина]. М.: Транспорт, 1990. 255 с.
3. Пугачев И.Н. Организация движения автомобильного транспорта в городах: учеб. пособие. Хабаровск: Изд-во ТОГУ, 2005. 196 с.
4. Клинковштейн Г.И., Афанасьев М.Б. Организация дорожного движения: учеб. для вузов. М.: Транспорт, 2001. 247 с.
5. Niittymaki J., Kikuchi S. Application of fuzzy logic to the control of a pedestrian crossing signal. J. Transp. Res. Bd., 1998, no. 1651, pp. 30–38.
6. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая ло- гика и искусственные нейронные сети. М.: Физматлит, 2001. 224 с.
7. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука, Физматлит, 1990. 272 с.
8. Павлов А.Н., Соколов Б.В. Принятие решений в условиях нечеткой информации: учеб. пособие. СПб: Изд-во ГУАП, 2006. 72 с.
9. Пегат А. Нечеткое моделирование и управление; [пер. с англ.]. М.: Бином, 2013. 800 с.
10. Marcian N.С., Dinu A., Khor J.G., McCormick M. Neural and Fuzzy Logic Control of Drives and Power Systems. Elrevier, Newnes Publ., 2002, 400 p.









