Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Применение a-задач в гарантированном оптимальном управлении инновационным развитием промышленных предприятий
Аннотация:Регулярное внедрение инноваций в производственные процессы предприятия, смена номенклатуры выпускаемой им продукции для более точного соответствия требованиям рынка являются необходимыми условиями выживания в конкурентной борьбе. Для учета влияния рисков и гарантии выполнения планов инновационного развития предлагается применение так называемых a-задач, предполагающих вероятностную оценку выполнимости ограничений математической модели объекта управления («мягкие ограничения»). Для удобства применения методов поиска решения вероятностные величины предлагается заменять интервалами их возможного изменения, применяя аппарат интервально-гарантированного оптимального управления. В статье дано описание сущности и диапазонов изменения компонент векторов и матриц a-задачи, являющихся правыми частями ограничений модели инновационного развития. Также предлагаются алгоритмы поиска решения внешней и внутренней задач для двухмодельной постановки задачи интервально-гарантированного оптимального управления инновационным развитием, учитывающие диапазоны изменения входных переменных и области допустимых решений. Информационные системы управления предприятием, позволяющие автоматизировать процессы оценки требований и условий внешней среды, оценки текущего состояния производственных процессов и ресурсов предприятия, управлять его функционированием, ставить цели и формировать план инновационного развития с учетом рисков, актуализировать их, предлагается называть АСУ инновационным развитием предприятия. В статье приводится функциональная модель процесса управления рисками и актуализации планов развития. Также дается описание информационной модели и сущностей БД, реализующих интервально-гарантированное управление инновационным развитием. Применение такого типа систем позволит гарантировать выполнение плана инновационного развития предприятия, если неопределенные параметры окажутся в указанных диапазонах их изменения.
Abstract:Regular introduction of innovations in production processes and changing a stock list to match market requirements is a necessary condition to survive in the competition. To account the impact of risks and ensure implementation of innovative development plans it is suggested to use so-called -tasks, which involve a probabilistic assessment of the control object mathematical model feasibility constraints (“soft limits”). The authors propose to replace probabilistic values by the intervals of their possible change for convenient using methods of finding a solution and apply interval-guaranteed optimal control. The article describes the nature and variations of -tasks vectors and matrices components, which are right-hand sides of innovative development model constraints. The paper also considers the algorithms of searching for external and internal problem solutions for a two-model problem formulation of the interval-guaranteed optimal management of innovative development. They take into account the variation ranges of input variables and feasible regions. Enterprise management information systems help to automate evaluating the requirements and external environment conditions, assessing the current status of production processes and resources of the enterprise, running its operation, setting goals and forming an innovative development plan considering risks, updating the goals. These information systems are suggested to call automated control systems of enterprise innovative development (ACSEID). The article presents a functional model of a risk management process and updating development plans. It also describes an information model and database entity, which implement interval-guaranteed management of innovative development. The use of ACSEID will ensure the implementation of the enterprise innovative development plan if the uncertain parameters are within the specified ranges of their change.
| Авторы: Матвейкин В.Г. (valery.mat@rambler.ru) - Тамбовский государственный технический университет (профессор), Тамбов, Россия, доктор технических наук, Дякин В.Н. (vadim_tmb@mail.ru) - Тамбовский государственный технический университет (докторант), Тамбов, Россия, кандидат экономических наук | |
| Ключевые слова: инновационное развитие предприятия, управление рисками, гарантированное управление |
|
| Keywords: enterprise innovative development, management of risk, guaranteed management |
|
| Количество просмотров: 7319 |
Версия для печати Выпуск в формате PDF (8.21Мб) Скачать обложку в формате PDF (1.09Мб) |
Инновационное развитие – необходимое условие выживания промышленных предприятий в условиях глобализации и повышения конкуренции. Инновации являются критическим фактором выживания и роста в современной среде [1]. В работе [2] отмечается динамический характер формирования новых возможностей при реализации инноваций, обеспечивающих долгосрочные конкурентные преимущества. Ввиду ограниченности инвестиционных ресурсов существуют проблемы отбора инновационных проектов, формирования оптимального портфеля в долгосрочной перспективе. Важную роль здесь играют доступность и актуальность информации о предприятии [3]. Необходимость осуществлять риск-менеджмент при управлении информационными пото- ками в бизнес-процессах отмечается в [4]. Функционирование предприятия осуществляется в условиях неопределенности состояния внешней и внутренней среды, что затрудняет выбор способа действий [5]. Учет неопределенности особенно важен в высокорисковых инновационных инвестиционных проектах развития с появлением новых технологий или продукции. Учет влияния рисков и гарантирование выполнения планов инновационного развития можно осуществить с использованием так называемых a-задач, предполагающих вероятностную оценку выполнимости ограничений математической модели объекта управления. Одной из концепций информационных систем управления предприятием, приведенных в [6], является управление устойчивым развитием предприятия (в иностранной терминологии Sustainability Management System или SMS), направленное на последовательное улучшение условий функционирования, повышение устойчивости социальных и экономических показателей. Вместе с тем в современных условиях ускорения циклов ввода в действие инноваций и частой смены производственных процессов становится необходимым расширение данной концепции и разработки АСУ инновационным развитием предприятий (ИРП). Применение такого типа систем позволит осуществлять устойчивое развитие предприятий при обновлении или смене существующих производств на более современные, отвечающие текущим или прогнозным требованиям рынка, определяя сроки ввода в действие инноваций и необходимый для этого инновационный потенциал. Постановка задачи и описание a-компонент задачи инновационного развития Двухмодельная постановка обобщенной задачи гарантированного управления, предложенная в [7] для управления химико-технологическими процессами, заключается в следующем. Необходимо отыскать A*=(
при выполнении условия
где m(A) и uA определяются алгоритмически:
при выполнении условий y=M(u); (4)
При этом
Условие (2) требует, чтобы вероятность выполнения системы ограничений и уравнений математической модели была не ниже заданного значения r. Уравнения вида y=M(u, v) из условия (2) соответствуют стохастической модели, а уравнения y=M(u) из условия (4) представляют детерминированную математическую модель. Условия (5) и (6) отражают два возможных вида неравенств в системе ограничений на возможные управления. Решение такой задачи происходит в два этапа. На первом этапе решается внутренняя задача (3)–(7), где при заданном A=(a1, …, an) ищутся оптимальные по критерию (3) управления uA. После этого определяется значение функции m(A)= =I(uA, M(uA)) при таком управлении uA. Полу- ченное значение функционала передается во внешнюю задачу, где отыскивается значение Чтобы избавиться от необходимости оперировать вероятностными величинами (как в условии (2)), представим параметры такого типа интервалами их изменения, применив оператор «[]». Это означает, что вероятностная величина в модели будет задаваться интервалом от ее минимального до максимального значения. Задача интервально-гарантированного управления, предложенная в [8], заключается в следующем. Требуется найти вектор Y=M(u, x), (8)
где Здесь уравнение (8) представляет собой детерминированную математическую модель внутренней модели задачи гарантированного оптимального управления. Для целей нашей задачи по управлению инновационным развитием наиболее подходит двухмодельная постановка задачи интервально-гарантированного управления для динамических моделей с сосредоточенными параметрами вида: Подробное описание двухмодельной постановки задачи интервально-гарантированного оптимального управления промышленным предприятием приводится в [9]. Для моделирования инновационного развития к постановке задачи из [9] добавляются производственные процессы, обновляемые после ввода в действие соответствующих инноваций по снижению норм затрат производственных ресурсов (если целью развития являлось снижение себестоимости), по повышению про- изводительности и новым параметрам произ- водственных функций, а в случае замены про- изводственных процессов для той же или новой продукции – с полной сменой норм затрат и производственных функций. Дополнительным ус- ловием инновационного развития становятся обеспечение необходимого инновационного потенциала, а также срок осуществления инноваций. В данной работе подробно опишем структуру компонент
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
где
Стоит отметить, что параметры Описание алгоритмов поиска решения Для поиска оптимальных значений правых частей ограничений Так как постановка задачи оптимального управления является двухмодельной и состоит из внешней и внутренней задач, удобно разбить алгоритм поиска на две части. Для поиска решения внешней задачи применяется алгоритм, изображенный на рисунке 1. Опишем его пошагово. Шаг 1. Задание начального значения правых частей ограничений Шаг 2. Генерация дополнительных 2q–1 точек, формирующих так называемый комплекс Шаг 3. Расчет оптимального управления Шаг 4. Проверка соответствия текущих точек комплекса точек условию прекращения поиска, то есть СКО£D. Шаг 5. Если условие прекращения поиска не выполнено, определяется наихудшая точка в комплексе путем поиска минимума: Шаг 6. Проверка допустимости новой точки xr по уравнениям математической модели и ограничениям. Шаг 7. Если новая точка xr допустима, происходит замена худшей точки xh на новую xr. Шаг 8. Сортировка обновленного комплекса точек (с xr) по максимуму. Шаг 9. Расчет СКО точек комплекса. Шаг 10. Если новая точка недопустима, уменьшаем ее на половину расстояния до центра остальных точек: xr=(xr+ xo)/2. Шаг 11. Если СКО£D, оптимальное решение найдено. Оно соответствует первой точке отсортированного по максимуму комплекса: Опишем алгоритм поиска решения внутренней задачи, показанный на рисунке 2. Шаг 1. Ввести Шаг 2. Генерация дополнительно 21 точки, формирующей комплекс Шаг 3. Расчет критерия оптимальности Шаг 4. Проверка соответствия текущих точек комплекса условию прекращения поиска, то есть СКО£D. Шаг 5. Если условие прекращения поиска не выполнено, определяется наихудшая точка в комплексе путем поиска минимума: Шаг 6. Проверка допустимости новой точки xr по уравнениям математической модели и ограничениям. Шаг 7. Если новая точка xr допустима, происходит замена худшей точки xh на новую xr. Шаг 8. Сортировка обновленного комплекса точек (с xr) по максимуму. Шаг 9. Расчет СКО точек комплекса. Шаг 10. Если новая точка недопустима, уменьшаем ее на половину расстояния до центра остальных точек: xr=(xr+ xo)/2. Шаг 11. Если СКО£D, оптимальное решение найдено. Оно соответствует первой точке отсортированного по максимуму комплекса: Предлагаемые поисковые алгоритмы построены по принципу комплексного метода Бокса для многомерного поиска при наличии ограничений на входные переменные и множество допустимых решений. Описание проекта модуля управления рисками инновационного развития Процесс управления рисками и актуализации планов развития АСУИРП, реализующий алгоритмы поиска решения двухмодельной постановки задачи интервально-гарантированного оптимального управления промышленным предприятием, описанной выше, представлен на рисунке 3 в формате IDEF0 (SADT) как в одном из наиболее используемых при моделировании бизнес-процессов и программных систем [10]. Вначале происходит формирование массивов для векторов и матриц двухмодельной постановки интервально-гарантированного управления инновационным развитием. После этого генерируются начальные значения управлений и правых частей ограничений (величин векторов ai). Далее во внешней задаче происходит поиск гарантированного оптимального значения критерия, управлений и правых частей ограничений при передаче их промежуточных значений во внутреннюю задачу, предполагающую поиск решения при отсутствии возмущений (они фиксируются на некотором уровне во внешней задаче). План инновационного развития и соответствующая ему двухмодельная постановка задачи могут быть скорректированы в процессе реализации планов развития и их актуализации. В этом случае происходит пересчет оптимальных управлений, обеспечивающих интервально-гарантированное выполнение скорректированного плана инновационного развития. Для сохранения расчетов модели интервально-гарантированного управления развитием предприятия применяются сущности, изображенные на рисунке 4. Сокращение «ИД» в ключевых полях таблиц на рисунке 4 обозначает идентификатор, который может представлять собой обычный счетчик записей либо являться классификатором. Обозначение «FK» соответствует внешнему ключу таблицы (Foreign Key). Оптимальные значения управлений функционированием получаются из сущностей «Управление продукцией», «Управление прибылью», «Управление займами», «Управление использованием займов», «Управление основными фондами», «Управление материалами», «Управление персоналом», используемых в процессе оптимального управления функционированием предприятия (без учета рисков). В этих же сущностях хранятся интервалы возможных изменений управлений и начальные значения правых частей ограничений. Параметры текущего состояния внешней среды хранятся в сущностях «Данные по рынкам сбыта», «Данные по рынкам труда», «Данные по рынкам основных фондов», «Данные по материалам» и «Данные по внешним НИОКР» процесса сбора и прогнозирования данных о внешней среде. Часть параметров, описывающих внешнюю или внутреннюю среду предприятия, являются возмущениями и носят неопределенный характер. Параметры текущего состояния предприятия хранятся с помощью сущностей «Результаты функционирования», «Нормы затрат на производство», «Производственные издержки», «Значения параметров производственных функций», «НИОКР предприятия», «Состояние основных фондов», «Состояние персонала», «Привлеченные финансы», «Данные по материалам». План инновационного развития, сроки и величина прироста инновационного потенциала и общих инвестиций хранятся в сущностях «План инновационного развития», «Потенциал НИОКР», «Потенциал материалов», «Потенциал основных фондов», «Потенциал персонала» и «Инвестиционный план» процесса определения целей и вида инновационного развития предприятия. Представление данных осуществляется в классификации типов управлений, возмущений и т.д., по одному или двум измерениям в зависимости от их типа, по установленному кванту разбиения времени в пределах периода планирования и для каждого расчета модели. Конкретное наполнение сущностей зависит от типа параметра модели в соответствии с ее описанием и особенностей продукции и предприятия, для которых выполняется расчет. Оптимальные значения критериев эффективности по каждому выполняемому расчету хранятся в сущности «Расчеты критериев моделей». После завершения расчетов и нахождения оптимальных управлений происходит их реализация путем копирования в сущности, соответствующие каждому типу управлений. При поступлении новых данных о ходе реализации плана инновационного развития возможны пересчет модели с актуальными параметрами и коррекция найденных ранее оптимальных управлений. В заключение отметим, что предложенная двухмодельная постановка задачи интервально-гарантированного оптимального управления инновационным развитием промышленного предприятия позволяет учесть влияние неопределенности параметров внешней и внутренней среды предприятия в высокорисковых инновационных инвестиционных проектах. Применение такой постановки задачи при построении систем типа АСУИРП позволит гарантировать выполнение плана инновационного развития, если неопределенные параметры окажутся в указанных диапазонах их изменения. Кроме того, такого типа система позволяет оперативно обновлять планы развития, актуализируя их по ходу выполнения. Литература 1. Yang Chen, Guiyao Tang, Jiafei Jin, Qinghong Xie, Ji Li. Transformational Leadership and Product Innovation Performance: The Roles of Corporate Entrepreneurship and Technology Orientation. CEOs’ Journ. of Product Innovation Management, 2014, vol. 31, no. S1, pp. 2–17. 2. Dixon S., Meyer K., Day M. Building Dynamic Capabilities of Adaptation and Innovation: A Study of Micro-Foundations in a Transition Economy. Long Range Planning, 2014, vol. 47, no. 4, pp. 186–205. 3. Spieth P., Lerch M. Augmenting innovation project portfolio management performance: the mediating effect of management perception and satisfaction. R and D Management, 2014, vol. 44, no. 5, pp. 498–515. 4. Xue Bai, Ramayya Krishnan, Rema Padman, Harry Jiannan Wang. On Risk Management with Information Flows in Business Processes. Information Systems Research, 2013, vol. 24, no. 3, p. 731–749. 5. Виноградов Г.П., Исаев А.А., Бурдо Г.Б. Согласованное принятие решений в производственных системах изготовления наукоемких изделий // Программные продукты и системы. 2015. № 2. С. 75–82. 6. Шуремов Е.Л., Заложнев А.Ю., Чистов Д.В. Эволюция и принципы построения информационных систем управления предприятием // Программные продукты и системы. 2014. № 2. С. 34–38. 7. Кафаров В.В., Бодров В.И., Матвейкин В.Г. Проблемы управления детерминированно-стохастическими моделями // Докл. АН СССР. 1989. Т. 308. № 3. С. 663–666. 8. Фролов С.В. Методы, алгоритмы и системы интервально-гарантированного оптимального управления технологическими процессами: дис. ... д-ра техн. наук. Тамбов: Изд-во Тамбов. гос. технич. ун-та, 1999. 481 с. 9. Дякин В.Н. Двухмодельная постановка задачи интервально-гарантированного оптимального управления промышленным предприятием // Системы управления и информационные технологии. 2015. № 1 (59). С. 29–34. 10. Усков А.А., Жуков А.Г. Подход к оценке сложности диаграмм SADT (IDEF0) // Программные продукты и системы. 2015. № 1. С. 34–37. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4028 |
Версия для печати Выпуск в формате PDF (8.21Мб) Скачать обложку в формате PDF (1.09Мб) |
| Статья опубликована в выпуске журнала № 3 за 2015 год. [ на стр. 57-66 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Особенности управления рисками торфяных пожаров на основе ГИС-технологий
- Нечеткая многокритериальная система поддержки принятия решений DecernsFMCDA
- Система многокритериального анализа решений DecernsMCDA и ее практическое применение
- Управление рисками в программных проектах высокой надежности
Назад, к списку статей



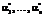 )ÎA, при котором достигает минимума функция
)ÎA, при котором достигает минимума функция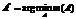 (1)
(1)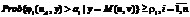 ,(2)
,(2) (3)
(3)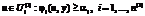 ; (5)
; (5)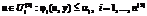 . (6)
. (6)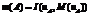 , A=(a1, …, an),
, A=(a1, …, an),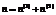 . (7)
. (7)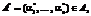 дающее оптимальное значение
дающее оптимальное значение 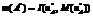 по критерию (1) при выполнении условия (2).
по критерию (1) при выполнении условия (2).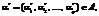
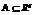 , при котором целевая функция m(a) достигает максимума:
, при котором целевая функция m(a) достигает максимума: 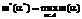 при выполнении условий:
при выполнении условий:  ,
, 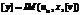 , где m(a) и ua определяются алгоритмически решением внутренней задачи
, где m(a) и ua определяются алгоритмически решением внутренней задачи  и выполняются следующие условия:
и выполняются следующие условия: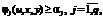

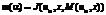 .
.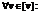
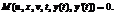
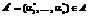 из постановки задачи гарантированного управления (1)–(7) для задачи управления инновационным развитием с учетом обозначений из [9]:
из постановки задачи гарантированного управления (1)–(7) для задачи управления инновационным развитием с учетом обозначений из [9]: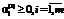 , (9)
, (9)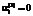 соответствует полному расходу материального ресурса вида i в размере
соответствует полному расходу материального ресурса вида i в размере 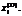 Положительные значения
Положительные значения 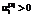 означают недоиспользование и формирование запасов производственных материалов;
означают недоиспользование и формирование запасов производственных материалов;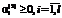 , (10)
, (10)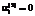 означает полную загрузку рабочих в соответствии с их календарем и общими объемами норма/часов работ в год, равными
означает полную загрузку рабочих в соответствии с их календарем и общими объемами норма/часов работ в год, равными 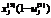 . Если же
. Если же  , часть работников вида i будет недоиспользоваться в производственных процессах;
, часть работников вида i будет недоиспользоваться в производственных процессах; , (11)
, (11)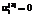 означает полную загрузку оборудования в соответствии с его календарем и общими объемами норма/часов работ в год, равными
означает полную загрузку оборудования в соответствии с его календарем и общими объемами норма/часов работ в год, равными  . Если же
. Если же 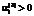 , часть оборудования вида i будет недоиспользоваться в производственных процессах;
, часть оборудования вида i будет недоиспользоваться в производственных процессах; , (12)
, (12)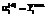 означает максимальную загруженность производственного процесса вида i в объемах, соответствующих емкости рынка. Если
означает максимальную загруженность производственного процесса вида i в объемах, соответствующих емкости рынка. Если 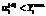 , предприятие не в полной мере реализует рыночные возможности по сбыту;
, предприятие не в полной мере реализует рыночные возможности по сбыту;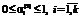 ;
;  , (13)
, (13)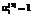 ,
, 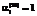 соответствуют направлению всех основных фондов вида i на НИОКР, а
соответствуют направлению всех основных фондов вида i на НИОКР, а  ,
, 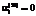 – на производство;
– на производство; ;
;  , (14)
, (14) ,
, 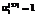 соответствуют направлению всего персонала вида i на НИОКР, а
соответствуют направлению всего персонала вида i на НИОКР, а  ,
,  – на производство;
– на производство;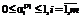 ;
;  , (15)
, (15)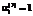 ,
, 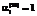 соответствуют направлению всех материалов вида i на НИОКР, а
соответствуют направлению всех материалов вида i на НИОКР, а 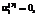
 – на производство;
– на производство; ;
; 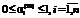 , (16)
, (16)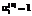 ,
, 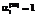 соответствуют направлению всей продукции вида i обратно в производство в качестве сырья или материалов,
соответствуют направлению всей продукции вида i обратно в производство в качестве сырья или материалов, 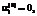
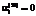 – вся продукции отправляется на сбыт конечным потребителям;
– вся продукции отправляется на сбыт конечным потребителям;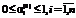 ;
; 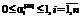 , (17)
, (17)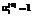 ,
,  соответствуют направлению всей прибыли от продажи продукции вида i на инвестиции, а
соответствуют направлению всей прибыли от продажи продукции вида i на инвестиции, а 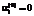 ,
,  – на выплату дивидендов или другие внешние цели;
– на выплату дивидендов или другие внешние цели; ;
;  , (18)
, (18)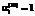 ,
,  соответствуют направлению всех инвестиций по виду фондов i на внешние по отношению к данному предприятию цели, а
соответствуют направлению всех инвестиций по виду фондов i на внешние по отношению к данному предприятию цели, а 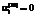 ,
, 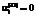 – на внутренние инвестиции в фонд вида i;
– на внутренние инвестиции в фонд вида i;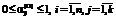 ;
;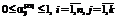 , (19)
, (19) ,
, 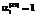 соответствуют направлению всей части внутренних инвестиций из прибыли от продажи продукции вида i на закупку основных фондов вида i, а
соответствуют направлению всей части внутренних инвестиций из прибыли от продажи продукции вида i на закупку основных фондов вида i, а  ,
,  означают неиспользование прибыли от продажи продукции вида i для внутренних инвестиций в основные фонды вида j;
означают неиспользование прибыли от продажи продукции вида i для внутренних инвестиций в основные фонды вида j;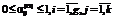 ;
; , (20)
, (20) ,
,  соответствуют направлению всей части внешних заимствований из источника вида i на закупку основных фондов вида i, а
соответствуют направлению всей части внешних заимствований из источника вида i на закупку основных фондов вида i, а  ,
, 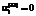 означают неиспользование внешних заимствований из источника вида i для внутренних инвестиций в основные фонды вида j;
означают неиспользование внешних заимствований из источника вида i для внутренних инвестиций в основные фонды вида j;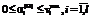 ;
;  , (21)
, (21) означает увольнение всего персонала вида i;
означает увольнение всего персонала вида i; ;
; 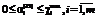 , (22)
, (22)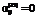 означает ликвидацию всех запасов материала вида i;
означает ликвидацию всех запасов материала вида i; ;
;  , (23)
, (23)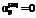 соответствует возврату всех взятых заимствований из источника вида i;
соответствует возврату всех взятых заимствований из источника вида i;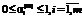 ;
;  , (24)
, (24)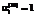 ,
,  означают полную потерю закупленных материалов вида i при доставке, а
означают полную потерю закупленных материалов вида i при доставке, а  ,
, 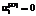 соответствуют случаю доставки материалов без затрат и потерь;
соответствуют случаю доставки материалов без затрат и потерь;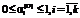 ;
;  , (25)
, (25)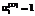 ,
, 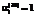 означают полный износ основного фонда вида i за рассматриваемый период времени, а
означают полный износ основного фонда вида i за рассматриваемый период времени, а 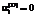 ,
, 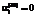 соответствуют отсутствию износа;
соответствуют отсутствию износа;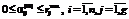 ;
;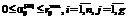 , (26)
, (26)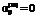 ,
, 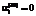 означают, что из прибыли от продажи продукции вида i проценты по заимствованиям вида j не выплачиваются;
означают, что из прибыли от продажи продукции вида i проценты по заимствованиям вида j не выплачиваются; ;
; 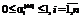 , (27)
, (27) ,
, 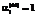 соответствуют достижению суммы степеней производственной функции по продукции вида i верхнего предела производительности, а
соответствуют достижению суммы степеней производственной функции по продукции вида i верхнего предела производительности, а 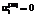 ,
,  означают отсутствие эластичности выпуска продукции вида i по затратам любого вида ресурсов (математическая абстракция);
означают отсутствие эластичности выпуска продукции вида i по затратам любого вида ресурсов (математическая абстракция);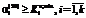 , (28)
, (28)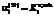 – минимальный уровень сохранности научного оборудования вида i;
– минимальный уровень сохранности научного оборудования вида i;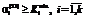 , (29)
, (29) соответствует минимальному уровню сохранности производственного оборудования вида i;
соответствует минимальному уровню сохранности производственного оборудования вида i;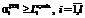 , (30)
, (30) соответствует минимальному уровню сохранности научного персонала вида i;
соответствует минимальному уровню сохранности научного персонала вида i; , (31)
, (31)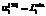 соответствует минимальному уровню сохранности производственного персонала вида i;
соответствует минимальному уровню сохранности производственного персонала вида i;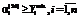 , (32)
, (32)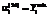 соответствует минимальному уровню сохранности объема производства по продукции вида i;
соответствует минимальному уровню сохранности объема производства по продукции вида i;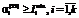 , (33)
, (33)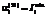 соответствует минимальному уровню сохранности инвестиций в основные фонды вида i;
соответствует минимальному уровню сохранности инвестиций в основные фонды вида i; устанавливают минимальный неотрицательный уровень параметров производственной функции.
устанавливают минимальный неотрицательный уровень параметров производственной функции. задают верхнюю границу изменения тех или иных параметров модели в соответствующем ограничении, а параметры
задают верхнюю границу изменения тех или иных параметров модели в соответствующем ограничении, а параметры 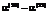 – нижнюю. Параметры
– нижнюю. Параметры 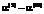 ,
,  имеют как верхнюю, так и нижнюю границы и задаются интервалом.
имеют как верхнюю, так и нижнюю границы и задаются интервалом.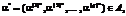 где q соответствует числу типов ограничений внутренней задачи (выше приведены типы таких ограничений, каждое из которых может в свою очередь являться вектором или матрицей значений), соответствующих им оптимальных управлений
где q соответствует числу типов ограничений внутренней задачи (выше приведены типы таких ограничений, каждое из которых может в свою очередь являться вектором или матрицей значений), соответствующих им оптимальных управлений  и значения целевой функции
и значения целевой функции 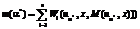 в задаче (40)–(82) из [9] предлагается воспользоваться следующими алгоритмами.
в задаче (40)–(82) из [9] предлагается воспользоваться следующими алгоритмами.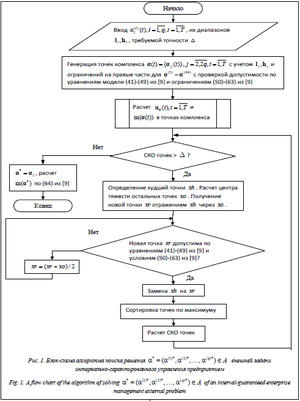
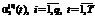 , с учетом размерности соответствующих векторов и матриц. Здесь же указываются возможные диапазоны изменения
, с учетом размерности соответствующих векторов и матриц. Здесь же указываются возможные диапазоны изменения 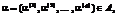 то есть
то есть  , с учетом их описания, приведенного выше. Кроме того, для контролирования завершенности поиска оптимальных значений
, с учетом их описания, приведенного выше. Кроме того, для контролирования завершенности поиска оптимальных значений 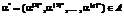 устанавливается величина
устанавливается величина  – минимальное значение среднеквадратического отклонения (СКО) точек комплекса от наилучшего значения.
– минимальное значение среднеквадратического отклонения (СКО) точек комплекса от наилучшего значения.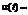
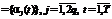 . Первая точка соответствует начальной точке, введенной на шаге 1. Остальные точки генерируются, во-первых, с учетом диапазона варьирования
. Первая точка соответствует начальной точке, введенной на шаге 1. Остальные точки генерируются, во-первых, с учетом диапазона варьирования  , и ограничений на правые части (9)–(33) из шага 1 и, во-вторых, с учетом уравнений математической модели (41)–(49) из [9] и ограничений (50)–(63) из [9].
, и ограничений на правые части (9)–(33) из шага 1 и, во-вторых, с учетом уравнений математической модели (41)–(49) из [9] и ограничений (50)–(63) из [9]. , и соответствующего значения целевой функции m(a(t)) в каждой точке комплекса
, и соответствующего значения целевой функции m(a(t)) в каждой точке комплекса 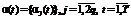 . Для этого используется алгоритм решения внутренней задачи, подробно изображенный на рисунке 2.
. Для этого используется алгоритм решения внутренней задачи, подробно изображенный на рисунке 2.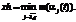 После сортировки точек комплекса она соответствует последней по индексу:
После сортировки точек комплекса она соответствует последней по индексу: 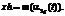 Далее происходит расчет центра тяжести остальных точек:
Далее происходит расчет центра тяжести остальных точек: 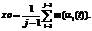 Затем происходит расчет значения функции в новой точке, полученной по следующему условию: xr=2,3xo–1,3xh.
Затем происходит расчет значения функции в новой точке, полученной по следующему условию: xr=2,3xo–1,3xh.

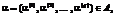 выбранные во внешней модели. Установить начальные управления
выбранные во внешней модели. Установить начальные управления  , с учетом размерности соответствующих векторов и матриц, диапазон их изменения
, с учетом размерности соответствующих векторов и матриц, диапазон их изменения  , с учетом условий (60), (61) из [9] и D – минимальное значение СКО точек комплекса для прекращения поиска.
, с учетом условий (60), (61) из [9] и D – минимальное значение СКО точек комплекса для прекращения поиска.
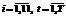 . Первая точка соответствует начальной точке, введенной на шаге 1. Остальные точки генерируются, во-первых, с учетом диапазона варьирования
. Первая точка соответствует начальной точке, введенной на шаге 1. Остальные точки генерируются, во-первых, с учетом диапазона варьирования 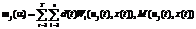 в каждой точке комплекса
в каждой точке комплекса 
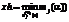 . После сортировки точек комплекса она соответствует последней по индексу:
. После сортировки точек комплекса она соответствует последней по индексу: 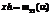 . Далее происходит расчет центра тяжести остальных точек:
. Далее происходит расчет центра тяжести остальных точек: 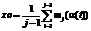 . Затем рассчитывается значение функции в новой точке, полученной по следующему условию: xr=2,3xo–1,3xh.
. Затем рассчитывается значение функции в новой точке, полученной по следующему условию: xr=2,3xo–1,3xh. и
и  .
.