Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Включение данных о размещении оборудования в графовую модель анализа обеспечения живучести корабля корабельными системами
Аннотация:Оценка живучести корабля основывается на способности его технических средств (корабельных систем) противостоять боевым и аварийным повреждениям, обеспечивая выполнение кораблем боевой задачи и предотвращение его катастрофы. Граф функциональных оценочных зависимостей является математической моделью, базирующейся на структурно-логических схемах зависимости выполнения операций корабельных систем от состояния элементов этих систем. Он предназначен для оценки живучести корабля при боевых и эксплуатационных повреждениях корабельных систем. Эта модель логически формально отражает функциональные зависимости между функционально значимыми элементами различного уровня агрегации оборудования корабельных систем при выполнении ими функционально самостоятельных операций. Внешние условия моделирования на графе функциональных оценочных зависимостей задаются моделями выхода из строя оборудования под воздействием поражающих факторов боевых и эксплуатационных повреждений. Предлагаемое в статье включение в граф функциональных оценочных зависимостей вершин состояния отсеков (помещений) корабля с дугами, отражающими размещение в них оборудования в соответствии с электронной моделью корабля, позволяет при незначительном увеличении размерности модели существенно уменьшить как общее количество вариантов исходных данных, так и количество целесообразно рассматриваемых вариантов. Такой подход дает возможность на единой модели выполнять вычислительно эффективный анализ живучести корабля, обеспечиваемой его системами независимо от причин выхода из строя их оборудования. Соответственно, вычислительная эффективность выполнения анализа позволяет расширить пространственно-функциональную вариативность моделирования с целью определения проекта корабля с наилучшей оценкой его живучести.
Abstract:Ship damage control evaluation is based on the ability of its technical means (ship systems) to withstand combat damage and emergency, ensure combat mission accomplishment and prevent its crash. Estimated functional dependency graph (EFDG) is a mathematical model based on structured-logical schemes of ship system operation performance dependence on the state of the elements of these systems. The graph is designed to estimate ship damage control in combat and operational damages of ship systems. This model logically formally reflects functional dependencies between functionally significant elements of various level of ship system equipment aggregation as they perform functionally independent operations. External simulation conditions on EFDG are set by equipment failure models caused by combat and operational damages. The article proposes including in EFDG the nodes of a ship sections (rooms) status with arcs reflecting equipment placement according to the electronic model of the ship. For a slight increase in model dimensionality, this significantly reduces the total number of original data and the amount of considered variants. Such approach allows performing an effective computational analysis of ship damage control for a single model, when this ship damage control is provided by its systems regardless of equipment failure causes. Thus, analysis computational efficiency allows extending the spatial and functional variability of modeling to determine a ship project with the best damage control assessment.
| Авторы: Сорокин В.Е. (sorokinve@yandex.ru) - НИИ «Центрпрограммсистем» (ведущий научный сотрудник), Тверь, Россия, кандидат технических наук, Болотов А.А. (andrey-bolotov@mail.ru) - НИИ «Центрпрограммсистем» (зав. группой), Тверь, Россия, Реут Е.В. (reutekaterina.cps.tver@gmail.com) - НИИ «Центрпрограммсистем» (ведущий инженер-программист), Тверь, Россия | |
| Ключевые слова: граф функциональных оценочных зависимостей, электронная модель корабля, боевые и эксплуатационные повреждения, оценка живучести, технические средства и системы корабля |
|
| Keywords: estimated functional dependency graph, ship digital model, combat and operational damage, survivability estimation, means and systems of a ship |
|
| Количество просмотров: 7817 |
Версия для печати Выпуск в формате PDF (8.31Мб) Скачать обложку в формате PDF (1.24Мб) |
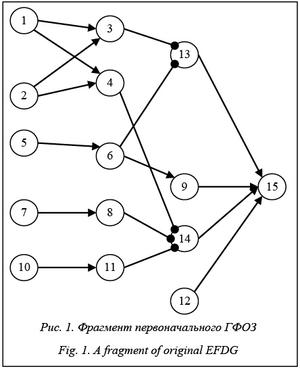
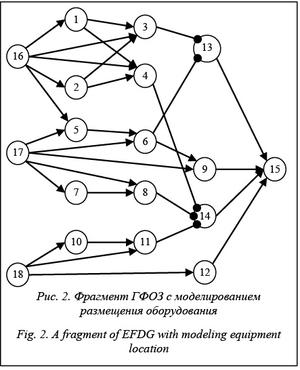
Произошедшие за последний век многочисленные аварии и катастрофы кораблей [1] специалисты в области военного кораблестроения связывают прежде всего с недостаточным обеспечением их живучести [2]. На сегодня сложилось устойчивое представление о том, что в основу оценки живучести корабля должна быть положена способность его технических средств противостоять боевым и аварийным повреждениям, обеспечивая выполнение боевой задачи и предотвращение катастрофы. Соответственно, оценка живучести корабельных систем при боевых и эксплуатационных повреждениях (БЭП) определяется в зависимости от обеспечения ими выполнения кораблем этих основных функций. За основу критериев оценки уровня живучести положен минимально необходимый уровень функционирования корабля, исключающий возникновение событий, ведущих к его катастрофе и/или к невыполнению им боевой зада- чи [3, 4]. Таким образом, данные критерии определяются полнотой решения корабельными системами задач по предотвращению этих событий. Выполнение каждой отдельно взятой задачи предотвращения одного из таких событий оценивается частным критерием, а всей их совокупности – общим критерием. Полноту достижения поврежденным кораблем общего или частных критериев безопасности характеризуют соответствующие показатели выполнения отдельной задачи или минимально необходимого уровня функционирования корабля, имеющие значение 1 при выполнении в полном объеме, 1/2 при частичном выполнении и 0 при невыполнении. Аналогично живучесть корабельной системы оценивается показателем выполнения функционально самостоятельной операции (ФСО), выполняемой этой системой по обеспечению минимально необходимого уровня функционирования корабля. При этом технические средства системы дезинтегрируются на функционально значимые элементы (ФЗЭ), то есть элементы системы, значимые в аспекте выполняемой ею операции. Показатели выполнения ФСО представляются конъюнкцией или дизъюнкцией логических функций состояний ФЗЭ [4, 5]. Такое определение критериев позволяет без существенной потери качества при оценке уровня живучести корабля перейти от вычислительно сложных логико-вероятностных методов ее определения [6, 7] к принципиально менее вычислительно сложной детерминированной технологии [5]. Графовые модели анализа обеспечения живучести корабля корабельными системами В качестве математической модели, позволяющей в наибольшей степени использовать стандартные методы расчета на графах для вычисления значений показателей выполнения ФСО в зависимости от исходных значений параметров состояния ФЗЭ при выполнении ОКР «Квартет», научно-технический отчет по которой имеет отраслевую регистрацию № 200436 от 29.04.2015 в Минпромторге России, был предложен граф функциональных оценочных зависимостей (ГФОЗ). Его прообразом послужила графоподобная структурно-логическая схема, на которой ФЗЭ, выявленные в результате анализа содержания ФСО, обозначаются прямоугольниками, исходящие из них ребра отражают их работоспособность, а вершины – логические связи между ними. На ГФОЗ моделируется логика влияния исходных состояний ФЗЭ на результирующие состояния ФЗЭ и выполнение частных и общей ФСО. Особенностью моделируемой логики яв- ляется ограниченность неполным монотонным базисом логических операций «И» и «ИЛИ», моделируемых дугами соответствующего типа. Достаточность монотонного базиса объясняется монотонностью моделируемых функциональных зависимостей. Вершины ГФОЗ, соответствующие ФЗЭ и ФСО, дополняются виртуальными вершинами, которые вводятся для реализации моделируемых функциональных зависимостей таким образом, чтобы в любую вершину входили только однотипные дуги. Такой подход сочетает наглядность ГФОЗ с возможностью использования методов расчета на графах, в которых, кроме структуры графа, используются только количественные (включая логические 0 и 1) параметры его вершин, соответствующие показателю выполнения ФСО или исходному и результирующему состояниям ФЗЭ, и параметр типа дуг [8]. Программную реализуемость данного подхода подтверждает свидетельство о госрегистрации программы для ЭВМ [9]. Отличительной особенностью этой программы является реализация ГФОЗ в структурах реляционной БД, а вычислительных алгоритмов – хранимыми процедурами этой БД. Эффективность программы базируется на соблюдении соответствия структуры наиболее вычислительно сложных SQL-запросов индексам БД [10]. Задание исходных данных для моделирования на ГФОЗ обеспечивается внешними моделями выхода из строя оборудования корабельных систем под воздействием поражающих факторов БЭП, такими как модели воздействия оружия, распространения пожара в помещении или затопления отсека корабля. Результатом работы этих моделей в большинстве случаев является выход из строя всего оборудования корабельных систем, размещенного в подверженном поражающим факторам БЭП помещении или отсеке. В то же время такое формирование исходных данных для моделирования на ГФОЗ, выполненное в рамках ОКР «Квартет», потребовало существенно больших вычислительных ресурсов, чем собственно моделирование на ГФОЗ. Включение в ГФОЗ данных о размещении оборудования корабельных систем Из изложенного следует, что возможно принципиально резкое упрощение формирования исходных данных для моделирования на ГФОЗ путем замены результатов моделирования выхода из строя оборудования под воздействием поражающих факторов БЭП на множество всего оборудования (или предопределенное по заданному критерию его подмножество), размещенного в определенном помещении или отсеке корабля. Такое задание исходных данных предоставляет упрощенные возможности анализа живучести корабельных систем для большинства случаев БЭП, заключающиеся в сокращении вычислительных потребностей. Одновременно возникают расширенные возможности анализа при моделировании на тех же вычислительных средствах принципиально большего количества вариантов как структуры ГФОЗ, так и вариантов исходных данных. С этой целью для моделирования размещения оборудования в первоначальный ГФОЗ предлагается добавлять вершины, соответствующие помещениям (отсекам) корабля, из которых выходят дуги в вершины ФЗЭ, оборудование которых в них размещено. Количественным параметром таких вершин является исходная работоспособность размещенного в помещении оборудования, для краткости называемого работоспособностью помещения. Если оборудование ФЗЭ размещено в нескольких помещениях (отсеках) таким образом, что ФЗЭ может считаться исходно работоспособным при работоспособном состоянии хотя бы одного из этих помещений, то в вершину этого ФЗЭ входят дизъюнктивные дуги (типа «ИЛИ»). Примером может служить включение в один ФЗЭ задублированного оборудования в разных помещениях (хотя целесообразнее такое оборудование выделять в отдельные ФЗЭ). В остальных случаях это конъюнктивные дуги (типа «И»). В качестве примера на рисунке 1 приведен фрагмент первоначального ГФОЗ для условной частной ФСО, на котором вершины 1–12 соответствуют ФЗЭ, вершины 13 и 14 виртуальные, а вершина 15 соответствует данной ФСО. В виртуальные вершины 13 и 14 входят дизъюнктивные дуги, а во все остальные вершины – конъюнктивные дуги. Исходными данными моделирования на этом графе является подмножество вершин ФЗЭ с неработоспособными исходными состояниями (для остальных вершин ФЗЭ принимается работоспособное исходное состояние). Количество возможных вариантов исходных данных равно двум в степени количества вершин ФЗЭ, для данного фрагмента ГФОЗ это 212=4096. Экспоненциальный рост количества вариантов от количества вершин ФЗЭ является существенным ограничением размерности ГФОЗ, на котором реально выполнимо моделирование для всех вариантов исходных данных. Дополненный вершинами 16–18 помещений (отсеков) размещения оборудования ФЗЭ первоначальный ГФОЗ приведен на рисунке 2. Дугами из вершин 16–18 в вершины ФЗЭ моделируется размещение оборудования ФЗЭ в соответствующих помещениях (отсеках). Так, оборудование ФЗЭ, моделируемое вершинами 1 и 12, размещается в помещениях (отсеках), моделируемых вершинами 16 и 18 соответственно, а оборудование ФЗЭ, моделируемое вершиной 5, размещается одновременно в двух помещениях (отсеках), моделируемых вершинами 16 и 17. Исходными данными моделирования на таком дополненном графе является подмножество вершин неработоспособных (в указанном выше смысле) помещений (отсеков). Количество возможных вариантов исходных данных равно двум в степени количества вершин помещений (отсеков), существенно меньшего количества вершин ФЗЭ. Для данного фрагмента ГФОЗ оно равно 23=8. При этом сложность структуры ГФОЗ в результате включения в него моделирования размещения оборудования возросла незначительно и расчет на нем требует практически тех же вычислительных ресурсов, так как максимальная длина пути на графе возросла только на 1. Такие количество вариантов и вычислительная сложность модели позволяют выполнять расчеты при полном переборе вариантов исходных данных, предоставляя возможности их сопоставительного анализа. В то же время реально имеет смысл далеко не полный перебор. Например, вариант при всех неработоспособных помещениях (отсеках) вообще не имеет смысла, а при их большинстве практически не реален. Как правило, достаточно ограничиться двумя или тремя одновременно неработоспособными помещениями (отсеками). Это дает возможность расширить сопоставительный анализ не только различными вариантами исходных данных, но и различными ГФОЗ, моделирующими как различные варианты размещения оборудования, так и проекты с различными структурно-функциональными связями между оборудованием. Перемещение оборудования ФЗЭ на таких ГФОЗ легко моделируется заменой дуги в вершину этого ФЗЭ из вершины одного помещения (отсека) на дугу из вершины другого помещения (отсека). Наконец, защищенное исполнение оборудования ФЗЭ, сохраняющее работоспособность при БЭП, моделируется отсутствием входящих в вершину таких ФЗЭ дуг из вершин помещений (отсеков). Учитывая реальную ограниченность таких конструктивно доступных вариантов, можно осуществить их полный перебор. Таким образом, дополнение ГФОЗ вершинами состояния отсеков (помещений) корабля с дугами, отражающими размещение в них оборудования, позволяет на единой математической модели с незначительным увеличением ее размерности выполнять вычислительно эффективный пространственно-функциональный анализ обеспечения живучести корабля его системами. Это предоставляет возможность на ранней стадии проектирования корабля вырабатывать рекомендации по структурно-функциональным преобразованиям и корректиров- кам размещения оборудования корабельных систем. Литература 1. AGCS Safety & Shipping 1912–2012 Report. URL: http://www.slideshare.net/AllianzKnowledge/agcs-safety-shipping-19122012-report-12288569 (дата обращения: 17.09.2015). 2. Живучесть корабля; [под ред. В.А. Коковина]. СПб: Левша. Изд-во Рос. инженер. акад. ВМФ, 2009. 376 с. 3. Алешин О.В., Андрющенко С.Л., Москаленко В.А., Поленин В.И., Соловьев С.Н. Критерии и количественно-качественные показатели для оценки живучести и безопасности кораблей ВМФ // Морская радиоэлектроника. 2012. № 1 (39). С. 1–11. 4. Лобанов С.Л., Бледнов Д.А. О безопасности и живучести кораблей ВМФ // Морской сборник. 2015. № 2. С. 39–44. 5. Лобанов С.Л., Бледнов Д.А., Сорокин В.Е. О технологии автоматизированной оценки живучести и безопасности кораблей ВМФ // Программные продукты и системы. 2014. № 2. С. 131–135. 6. Рябинин И.А., Черкесов Г.Н. Логико-вероятностные методы исследования надежности структурно-сложных систем. М.: Радио и связь, 1981. 286 с. 7. Поленин В.И., Рябинин И.А., Свирин С.К., Гладко- ва И.А.; [под ред. А.С. Можаева]. Применение общего логико-вероятностного метода для анализа технических, военных и организационно-функциональных систем и вооруженного противоборства. СПб: Изд-во РАЕН, 2011. 416 с. 8. Сорокин В.Е., Реут Е.В. Комбинированный подход к реализации оценки живучести технических средств (систем) корабля при боевых повреждениях с учетом накопления ущерба // Программные продукты и системы. 2014. № 3. С. 97–105. 9. Болотов А.А., Сорокин В.Е. Оценка живучести корабля вследствие изменения состояния корабельных систем и комплексов с учетом повреждения оборудования, выхода его из действия. Свид. о гос. регистр. прогр. для ЭВМ № 2015618858. Бюл. № 9 (107). 2015. 10. Сорокин В.Е. Метод искусственного соответствия SQL-запросов индексам реляционных баз данных // Программные продукты и системы. 2013. № 2. С. 47–54. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4101 |
Версия для печати Выпуск в формате PDF (8.31Мб) Скачать обложку в формате PDF (1.24Мб) |
| Статья опубликована в выпуске журнала № 1 за 2016 год. [ на стр. 13-16 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик: