Целью данной работы является математическое описание процессов на границе шлак-металл в колонном струйно-эмульсионном реакторе (СЭР) по двум схемам (диффузионный переход на границе шлак-металл и обезуглероживание частиц железа в слое шлака) и создание алгоритмов для двух схем в рамках имитационной модели гравитационного сепаратора СЭР [1]. Данные механизмы описывают окислительные процессы, происходящие в нижней части колонного реактора и влияющие на содержание углерода в конечном продукте – металле.
Для описания механизмов в агрегате СЭР был применен принцип мозаичной неравновесной термодинамики, состоящий в выделении диссипативных структур в колонном реакторе, которые существуют только при условии протекания процесса в определенном кинетическом режиме. Целевые задачи имитационной модели СЭР представлены на рисунке 1.
Для решения задачи был выбран метод имитационного моделирования (Монте-Карло). Первоначально он использовался в основном для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными, однако не утратил актуальности и на сегодняшний день [2]. Большинство методов реализуют генерацию случайности по одной координате [3], реже встречаются задачи двухмерного [4] и трехмерного моделирования [5]. Анализ готовых средств имитационного моделирования [6, 7] показывает, что для их использования требуется знание инструментальной среды, а для гибкого взаимодействия – знание языка среды. Использование объектно-ориентированных языков программирования позволит создать более сложную систему имитационного моделирования. Авторы рассматривали объектно-ориентированные языки программирования Delphi [8], Visual C# [9] и ActionScript 3.0 [10, 11]. Язык ActionScript [12, 13] известен благодаря Flash-роликам и Flash-играм, в которых используется большое количество взаимодействующих объектов на сцене, поэтому он и был выбран для анимации движения частиц в колонном реакторе.
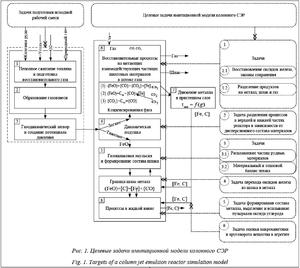 Одной из важнейших диссипативных структур, более подробно рассмотренных в [14, 15], является гравитационный сепаратор металла, шлака и газа, образующийся в верхней половине колонного реактора (зоны 6 и 7 на рисунке 1). Из-за влияния гравитационной составляющей и близкого к параболическому распределению вектора скорости дви- жения эмульсии в поперечном сечении колонного реактора имеет место сепарация частиц в зависимости от их плотности. Вследствие этого явления частицы восстановленного железа, имеющие плотность, в два–три раза большую, чем частицы оксидов железа, «скатываются» на периферию потока и образуют пристенный слой с отрицательной (обратной) скоростью (зона 7). Это явление визуально наблюдалось авторами на физической модели.
Одной из важнейших диссипативных структур, более подробно рассмотренных в [14, 15], является гравитационный сепаратор металла, шлака и газа, образующийся в верхней половине колонного реактора (зоны 6 и 7 на рисунке 1). Из-за влияния гравитационной составляющей и близкого к параболическому распределению вектора скорости дви- жения эмульсии в поперечном сечении колонного реактора имеет место сепарация частиц в зависимости от их плотности. Вследствие этого явления частицы восстановленного железа, имеющие плотность, в два–три раза большую, чем частицы оксидов железа, «скатываются» на периферию потока и образуют пристенный слой с отрицательной (обратной) скоростью (зона 7). Это явление визуально наблюдалось авторами на физической модели.
Таким образом, с учетом противодействия гравитационных и аэродинамических сил в верхней половине колонного реактора (зона 6) происходит сепарация металла и шлака, а также образуется неравномерное (по плотности, газосодержанию и химсоставу) распределение параметров по высоте агрегата. Распределенность содержания оксидов железа по высоте, что играет важную роль в управлении соотношением восстановительных и окислительных процессов, обусловливается также термодинамически неравновесным характером процессов, в том числе интенсивными потоками вещества и энергии, поступающими снизу через соединительный канал 3 из реактора-осциллятора 2.
Учитывая важную, по существу центральную, роль отмеченной диссипативной структуры, связывающей все остальные зоны и обусловливающей круговорот веществ в агрегате, для ее изучения создана имитационная модель [14, 15], в которой в качестве «первых принципов» – элементов нижнего уровня иерархии – выступают дисперсные частицы шихты с реально заданным гранулометрическим распределением. Ядром этой модели является задача обтекания единичной частицы вертикальным потоком несущего реакционного газа.
В процессе плавления частицы железной руды образуются частицы металла, шлака и газа. Частицы металла из-за гравитационных сил попадают в копильник (зона 8). Частицы шлака, не повстречавшие частицы газа, попадают на верхнюю границу металла и образуют слой шлака (зона 5). Данный слой шлака будет накапливаться до тех пор, пока высота шлака не достигнет соединительного канала (зона 3), который будет «сдувать» частицы шлака.
В данной статье основное внимание уделено алгоритмам двух следующих моделей:
- диффузионный переход на границе шлак-металл (зоны 5–8);
- процессы, протекающие при прохождении частицы металла через шлак.
Стоит также отметить, что ранее в имитационный модели был задействован только первый механизм [14].
Математическая постановка задачи диффузионного перехода на границе шлак-металл
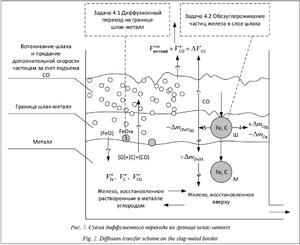 На рисунке 2 показаны процессы, происходящие в зонах 5–8 колонного СЭР.
На рисунке 2 показаны процессы, происходящие в зонах 5–8 колонного СЭР.
Сначала рассмотрим задачу диффузионного перехода на границе шлак-металл.
1. Крупные частицы железной руды из-за плотности и сил, действующих на них, плавятся в слое шлака. Диффузионный переход на границе шлак-металл определяется следующим соотношением:
 , (1)
, (1)
где (FeO)Ш – содержание FeO в шлаке; (FeO)РШМ – содержание FeO, равновесное с металлом; βШМ – коэффициент массоотдачи из шлака в металл.
 , (2)
, (2)
где L – коэффициент распределения между шлаком и металлом; [O]РМ – равновесное содержание кислорода в металле.
 , (3)
, (3)
где PCO – давление в пузырьках CO; [C]М – содержание углерода в металле.
2. В результате диффузионной силы, определенной по формуле (1), осуществляется переход кислорода из шлака в металл, диссоциация FeO:
(FeO)→[Fe] + [O],
а затем [O] + [C] = {CO}. (4)
Объемы компонентов углерода, железа и оксида углерода, образовавшиеся в результате диссоциации FeO, рассчитываются по формулам  ,
,  ,
,  , где Мм – масса металла.
, где Мм – масса металла.
3. Осуществляется подъем газовых пузырей CO, образовавшихся в результате диссоциации FeO по формуле (4).
Задача обезуглероживания частиц железа в слое шлака.
4. Из частицы железа, проходящей через слой шлака, выгорает углерод: Δmc = mKΔC, где mK – масса капли; ΔC – процент обезуглероживания; ΔC= W×tпр, где W – скорость обезуглероживания; τпр – время пребывания капли в слое шлака.
5. При выгорании углерода в шлак попадает часть оксида железа пропорционально массе сгоревшего углерода:  .
.
6. Осуществляется переход железа из шлака в металл:
 . (5)
. (5)
7. Образуется газовый пузырь в результате сгорания углерода:  .
.
Структура имитационной модели гравитационного сепаратора
Прежде чем переходить к алгоритмам на границе шлак-металл, рассмотрим общую структуру имитационной модели (рис. 3).
Как видно из рисунка 3, основной модуль взаимодействует со всеми классами. Классы руды, металла, шлака, металла внизу и шлака внизу вызывают класс расчетов. При этом визуализация частиц и статистических данных происходит в основном модуле, как и взаимодействие с пользова- телем, а отображение графиков – в соответствующем классе.

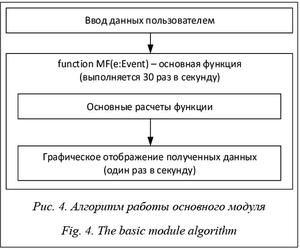 Стоит также отметить, что в основном модуле и классах конденсированных частиц и газов перерасчеты происходят 30 раз в секунду (например, определение нового положения частицы в колонном реакторе). На рисунке 4 показан алгоритм работы основного модуля, в котором выделены два этапа: ввод и инициализация данных, а также вызов основной функции MF.
Стоит также отметить, что в основном модуле и классах конденсированных частиц и газов перерасчеты происходят 30 раз в секунду (например, определение нового положения частицы в колонном реакторе). На рисунке 4 показан алгоритм работы основного модуля, в котором выделены два этапа: ввод и инициализация данных, а также вызов основной функции MF.
В основных расчетах функции MF() выполняется ряд задач:
- инициализация переменных и массивов;
- добавление новых частиц с заданной дискретностью;
- расчет плотности по газу;
- расчет изменений состава шлака и металла при диффузионном переходе на границе шлак-металл;
- образование частиц шлака, если высота шлака достигла входного отверстия потока газовзвеси;
- расплавление частицы и образование металла, шлака и газа;
- учет изменений металла и шлака при достижении частицей металла нижней границы шлака;
- удаление частиц, достигших выходного отверстия;
- расчеты упругих и неупругих ударов между частицами;
- определение плотности слоев по высоте канала;
- накопление статистических данных об исследуемом объекте и их отображение.
Алгоритмы процессов на границе шлак-металл
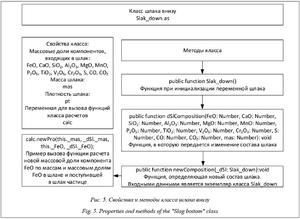 Прежде чем обратиться к алгоритму взаимодействия на границе шлак-металл, рассмотрим структуру класса шлака внизу. Данный класс создан для учета изменения материального баланса шлакового слоя, методы и функции которого представлены на рисунке 5.
Прежде чем обратиться к алгоритму взаимодействия на границе шлак-металл, рассмотрим структуру класса шлака внизу. Данный класс создан для учета изменения материального баланса шлакового слоя, методы и функции которого представлены на рисунке 5.
В классе учитываются массовые доли входящих компонентов, масса и плотность шлака. Переменная для вызова класса расчетов является скрытой и может вызываться только экземпляром данного класса.
При инициализации данного класса все значения по умолчанию приравниваются к 0. Частица шлака, образованная в результате расплавления частицы металла, попадает в нижний слой шлака. Вызывается функция приращения шлака, в которую передаются массовые проценты и масса частицы шлака, затем определяется новый состав шлака. Если это первая частица, которая попадает в шлаковый слой, то состав шлакового слоя будет идентичен составу частицы. Постепенно происходит накопление массы шлака внизу до тех пор, пока высота шлакового слоя не достигнет входного канала. В этом случае частицы шлака определенной крупности будут отрываться от шлакового слоя, соответственно, в функцию изменения состава шлака будет передаваться масса со знаком минус.
Как видно из рисунка 5, в функции определения нового состава шлака идет вызов функции класса расчетов, в котором по входным данным (массам и массовым долям заданного компонента) рассчитывается новая массовая доля в результате прихода или ухода какого-то вещества. Для шлака вызов данной функции происходит 12 раз, так как в шлаке учитываются 12 компонентов.
Устройство класса металла внизу аналогично классу шлака внизу, за исключением компонентов, входящих в металл (S, Fe, С, Mn, P).
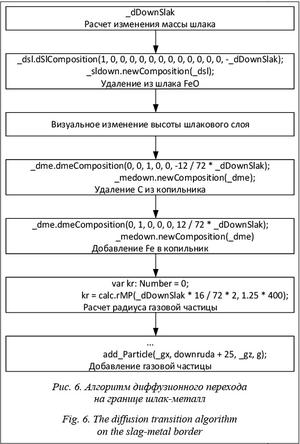
 Алгоритм диффузионного перехода показан на рисунке 6.
Алгоритм диффузионного перехода показан на рисунке 6.
Алгоритм диффузионного перехода на границе шлак-металл (рис. 6) состоит из определения массы шлака, удаления FeO из шлака, удаления С из копильника, добавления Fe в копильник, образования газового пузыря CO, визуального отображения изменения высоты шлакового слоя и отображения образовавшейся газовой частицы.
Рассмотрим более подробно алгоритм расчета изменения массы шлака (рис. 7). Для расчета массы шлака, прореагировавшего в результате диффузионного перехода, необходимо знать балансное содержание FeO (по формуле (2)) и скорость восстановления на границе шлак-металл (по формуле (1)). Эти две функции расположены в классе расчетов. Для знания балансового содержания FeO требуется передать в функцию содержание углерода. А для расчета скорости обезуглероживания передаются содержание FeO в шлаке и балансное FeO (формула (3)), рассчитываемое в соответствующей функции.
Перейдем к рассмотрению второго алгоритма обезуглероживания частицы железа в слое шлака. Напомним, что частица железа образуется в результате расплавления железной руды и под действием силы тяжести проходит через слой шлака. Алгоритм прохождения представлен на рисунке 8.

Алгоритм обезуглероживания частицы железа в слое шлака состоит из следующих пунктов:
1) определение массы частицы железа в килограммах;
2) определение массы частицы в модельных единицах измерения;
3) определение времени пребывания частицы в шлаке по плотности и радиусу;
4) удаление углерода из частицы железа с учетом скорости выгорания углерода и времени пребывания частицы в железе;
5) инициализация выделившегося из шлака металла (формула (5)), вычисление новой плотности металла;
6) определение нового состава шлака с учетом того, что из него выделился FeO;
7) создание газовой частицы CO;
8) учет прироста массы железа, пришедшей из шлака;
9) определение нового состава металла в копильнике.
Как видно из рисунка 7, в алгоритме используются данные о частицах железа, которые берутся из класса конденсированных частиц (пп. 1–6, 9). Принадлежность к частицам железа определяется по идентификатору.
В пп. 1–3 происходит обращение к классу расчетов, в котором рассчитываются масса частицы по радиусу и плотности (пп. 1 и 2) и время нахождения частицы металла в шлаке (п. 3).
Время растворения влияет на выгорание углерода из частицы металла (п. 4), определение выделившегося из шлака металла (п. 5), радиуса частицы металла (п. 6), состава шлака (п. 7) и объема частицы газа, образовавшейся в результате реакции (п. 8).
С учетом пришедшего из шлака металла (п. 9) и частицы металла определяется состав металла в копильнике (п. 10).
Алгоритм обезуглероживания частицы металла в шлаке взаимодействует с другими классами программы: классом расчетов (пп. 1–3, 6, 8, 9), классом конденсированных частиц (пп. 1–6, 9), классом газовых частиц (п. 8), классом металла (пп. 5, 9), классом шлака внизу (п. 7), классом металла в копильнике (п. 10).
Таким образом, в статье рассмотрены математическая постановка задачи и алгоритмы на границе шлак-металл. Особенностью алгоритма является применение объектно-ориентированного подхо- да – разбиение сложного объекта на более простые в виде классов: конденсированных частиц, газовых частиц, шлака внизу, металла внизу. В каждом из классов выделяются необходимые для изучения методы. При этом количество экземпляров класса, например частиц, ограничивается вычислительной мощностью компьютера. Такой подход обладает гибкостью, так как разработанные классы (или некоторые функции классов) могут быть использованы при разработке других задач. В результате проведенных модельных исследований показано, что при реализации только первого механизма содержание углерода в конечном продукте составляет 4 %, а при реализации двух отмеченных выше схем – 3,5 %, что свидетельствует о возможности более гибкого управления процессом обезуглероживания.
Литература
1. Цымбал В.П., Мочалов С.П., Рыбенко И.А. и др. Процесс СЭР – металлургический струйно-эмульсионный реактор. М.: Металлургиздат, 2014. 488 с.
2. Kroese D.P., Brereton T., Taimre T., Botev Z.I. Why the Monte Carlo method is so important today. WIREs Comput Stat, 2014, no. 6, pp. 386–392.
3. Милованов М.М. Разработка инструментальной системы имитационного моделирования бизнес-процессов предприятия // Моделирование, программное обеспечение и наукоемкие технологии в металлургии: сб. докл. III Всерос. науч.-практич. конф. Новокузнецк: Изд-во СибГИУ, 2011. С. 262–266.
4. Меликов А.В. Имитационная модель оценки эффективности стрельбы подразделений РСЗО // NB: Кибернетика и программирование. 2014. № 3. С. 91–102.
5. Гришко М.С., Безносюк С.А., Жуковский М.С. Компьютерное моделирование методом Монте-Карло процессов фор- мирования кластеров никеля в нанопорах материалов // Изв. Алтайского гос. ун-та. 2007. № 3. С. 71–75.
6. Карпов Ю.Г. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5. СПб: БХВ-Петербург, 2009. 400 с.
7. Лычкина Н.Н. Современные технологии имитационного моделирования и их применение в информационных бизнес-системах и системах поддержки принятия решений // Имитационное моделирование. Теория и практика (ИММОД-2005): сб. докл. II Всерос. науч.-практич. конф. СПб: Изд-во ЦНИИТС, 2005. Т. 1. С. 25–31.
8. Кожемяченко В.И. Программирование в среде Delphi. В 2 ч. Новокузнецк: Изд-во СибГИУ, 2015. Ч. 1. 32 с.
9. Кожемяченко В.И. Программирование в среде Visual С#. В 2 ч. Новокузнецк: Изд-во СибГИУ, 2012. Ч. 2. 54 с.
10. Изучение ActionScript 3.0. URL: http://help.adobe.com/ ru_RU/as3/learn/as3_learning.pdf (дата обращения: 21.02.2016).
11. Справочник по AcionScript 3.0 для платформы Adobe Flash. URL: http://help.adobe.com/ru_RU/FlashPlatform/reference/ actionscript/3/ (дата обращения: 21.02.2016).
12. Лотт Дж., Шалл Д., Питерс К. ActionScript 3.0. Сборник рецептов. СПб: Символ-Плюс, 2007. 608 с.
13. Мук К. ActionScript 3.0 для Flash. Подробное руководство. СПб: Питер, 2009. 992 с.
14. Сеченов П.А. Алгоритм и программная реализация имитационной модели гравитационного сепаратора колонного струйно-эмульсионного реактора // Программные продукты и системы. 2015. № 3 (111). С. 214–219.
15. Цымбал В.П., Сеченов П.А., Оленников А.А., Падал- ко А.Г. Имитационное моделирование гетерогенного потока и проблема уравнения Навье-Стокса // Соврем. науч. достижения металлург. теплотехники и их реализация в пром-ти: сб. докл. Междунар. научн.-практ. конф. Екатеринбург: Изд-во УрФУ, 2015. С. 357–365.





 , (1)
, (1) , (2)
, (2) , (3)
, (3) ,
,  ,
,  , где Мм – масса металла.
, где Мм – масса металла. .
. . (5)
. (5) .
.





