Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Метод повышения интерпретируемости регрессионных моделей на основе трехступенчатой модели развития мышления
Аннотация:Повышение обобщающей способности регрессионных моделей приводит к более эффективному решению задач распознавания, прогнозирования, выявления различных стратегий поведения технических и социальных систем. Известные методы повышения обобщающей способности обладают вычислительной эффективностью, но понижают интерпретируемость модели и конечных результатов. Предлагаемая статья является попыткой обратиться к данной проблеме, дополняя задачи регрессии и классификации в контексте задач синтеза фильтров из области цифровой фильтрации и тестирования из области психометрии. Принимая во внимание достоинства решений в альтернативных предметных областях, целью данной работы является создание метода повышения интерпретируемости регрессионных моделей через стимулирование процессов внутренней неопределенности в машинном обучении. Для достижения поставленной цели была создана трехступенчатая модель развития машинного мышления, отражающая динамику анализируемых предметных областей. Эти области связаны едиными процессами внутренней неопределенности, что требует создания соответствующего математического аппарата. Данная работа рассматривает процессы внутренней неопределенности с когнитивной точки зрения через процессы забывания и угадывания. Результатом исследования является реализация ступеней синтеза фильтров, тестирования и интегральной ступени регрессии/классификации в рамках созданной трехступенчатой модели развития мышления. При этом ступень синтеза фильтров моделирует техническую среду, ступень тестирования – социальную среду, а интегральная ступень – социально-техническую среду. Тогда как социальная среда моделирует сознание человека, социально-техническая среда вводит понятие сознания машины. Представленные реализации позволили формализовать метод повышения интерпретируемости регрессионных моделей через формирование принципов перехода от сознания человека к сознанию машины.
Abstract:Increasing generalization performance of regression models leads to a more effective solution for the problems of recognition, prediction, and extraction of social and engineering behavior strategies. A number of known methods for improving the generalization properties demonstrate computational effectiveness, hovewer they reduce interpretability of a model and results. This study is an attempt to approach this problem looking at the methods of regression and classification from digital filtering and psychometrics points of view. Considering the advantages of the methods for solving the interpretability problem in these areas, this research is aimed at defining a method to improve the interpretability of regression models by promoting learner’ internal uncertainty in machine learning. In order to solve the problem, the author has developed a three-step model of building cognition. This model reflects direct relations among digital filtering, psychometrics, and machine learning. These research areas employ the same sources of internal uncertainty that makes creating consistent mathematical models that connects the areas possible. For this purpose, the paper considers internal uncertainty from a cognitive point of view as processes of forgetting and guessing. The findings of this study provide the implementations of the following steps in accordance with the tree-step model: a filter synthesis step, a psychological assessment step, and an integrated regression/classification step. While the first step models an engineering environment and the second step presents a social environment, the integrated step helps to create a social-engineering environment. In addition, in contrast to the social environment that may simulate human cognition, the social-engineering environment seems promising in introducing machine cognition. The proposed implementations allow formalizing the method for improving interpretability of regression models changing from one kind of cognition to the other.
| Авторы: Куликовских И.М. (kulikovskikh.i@gmail.com) - Самарский государственный аэрокосмический университет им. С.П. Королева (национальный исследовательский университет) (доцент), Самара, Россия, кандидат технических наук | |
| Ключевые слова: философская система гегеля, внутренняя неопределенность, психометрия, цифровая фильтрация, машинное обучение |
|
| Keywords: hegel’s philosophical system, internal uncertainty, psychometrics, digital filtering, machine learning |
|
| Количество просмотров: 6906 |
Статья в формате PDF Выпуск в формате PDF (29.80Мб) |
Создание эффективных методов и алгоритмов с высокой обобщающей способностью является основной задачей машинного обучения [1–3]. С целью повышения обобщающей способности было предложено множество методов усиления моделей регрессии и классификации [1]. К наиболее эффективным методам усиления моделей обучения относятся различные методы понижения размерности, методы регуляризации и композиционные методы. Первые две группы методов способствуют разрешению компромисса между переобучением и недообучением, тогда как усиление обучающих моделей через построение их композиций обеспечивает меньшую восприимчивость к переобучению за счет адаптивности данного класса алгоритмов. Однако, несмотря на их вычислительную эффективность, композиционные методы, как и другие методы усиления, обладают существенным недостатком, связанным с плохой интерпретируемостью моделей [4], а следовательно, и конечных результатов. Данная работа является попыткой обратиться к этой проблеме, дополняя задачи регрессии и классификации в контексте задач синтеза фильтров из области цифровой фильтрации и тестирования из области психометрии соответственно. Целями слияния понятий в предметных обла- стях являются углубление понимания проблемы интерпретируемости и формирование соответству- ющего математического аппарата для нахождения более эффективных решений. В качестве инстру- мента слияния задач регрессии и синтеза фильтров явились понятия информативности признаков и сложности фильтров. При этом первое понятие задается совокупностью важных признаков в модели обучения, а второе – порядком модели фильтра. В свою очередь, инструментом слияния задач классификации и тестирования явились понятия эффектов «пола» и «потолка» [5–11]. Наиболее эффективное решение задачи синтеза фильтров связано с оптимизацией полюсов модели фильтра [12, 13], тогда как эффективность результатов тестирования связывают с необходимостью выработки метакогнитивной стратегии у обучаемых (тестируемых) [9, 10]. Но оба решения можно представить как введение в рассмотрение дополнительного параметра исследуемой модели, описывающего ее внутреннюю неопределенность (неоднозначность). Принимая во внимание достоинства данных альтернативных решений, целью данной работы является создание метода повышения интерпретируемости регрессионных моделей через стимулирование процессов внутренней неопределенности в машинном обучении. Трехступенчатая модель развития машинного мышления
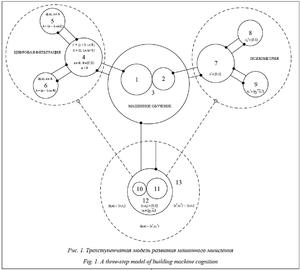
Данная трехступенчатая модель развития машинного мышления, отражающая динамику анализируемых предметных областей, связана едиными процессами внутренней неопределенности, что требует создания соответствующего математического аппарата (рис. 1). С этой целью в работе рассматриваются процессы внутренней неопределенности с когнитивной точки зрения через процессы забывания и угадывания. В цифровой фильтрации забывание описывается через параметр затухания (забывания) [16–18] при оценивании коэффициентов модели фильтра методом взвешенных наименьших квадратов. В когнитивной психологии и психометрии стимулирование процессов забывания и угадывания [19–23] и психометрии [24–26] позволяет исключить эффекты «пола» и «потолка» при оценивании уровня мышления обучаемых. Модели оценивания уровня мышления обучаемых имеют вид логистической регрессии, коэффициенты которой также оцениваются методом наименьших квадратов с итерационным перевзвешиванием. Нако- нец, в машинном обучении присутствие эффектов «пола» и «потолка» может указывать на наличие идеальной разделимости классов, а следовательно, слабой обучаемости модели [27, 28]. Таким образом, предлагаемая интерпретация в терминах забывания и угадывания позволяет свести разработку методов стимулирования процессов внутренней неопределенности к единому математическому аппарату. Приведем интерпретацию цифровых обозначений, используемых на рисунке 1. 1. Анализ методов усиления моделей регрессии (модель линейной регрессии). 2. Анализ методов усиления моделей классификации (модель логистической регрессии). 3. Методы стимулирования внутренней неопределенности в машинном обучении. 4. Методы стимулирования внутренней неопределенности в цифровой фильтрации через параметр ϕ. При этом предполагается, что α = 0. 5. Методы стимулирования внутренней неопределенности в цифровой фильтрации через пару параметров (ϕ, α), где α Î Z. 6. Методы стимулирования внутренней неопределенности в цифровой фильтрации через пару параметров (ϕ, α), где α Î R. 7. Методы стимулирования внутренней неопределенности в психометрии через вероятностный параметр c. 8. Методы стимулирования внутренней неопределенности в психометрии через нечеткий параметр c при индивидуальном обучении. 9. Методы стимулирования внутренней неопределенности в психометрии через нечеткий параметр c при групповом обучении. 10. Реализация ступени синтеза фильтров, моделирующей техническую среду. 11. Реализация ступени тестирования, моделирующей социальную среду. 12. Реализация интегральной ступени регрессии/классификации, моделирующей социально-техническую среду. 13. Метод повышения эффективности регрес- сионных моделей через формирование принципов перехода от сознания человека к сознанию машины. Метод повышения интерпретируемости регрессионных моделей Рассмотрим реализацию ступеней графической модели (рис. 1, цифровые обозначения 10–13) более подробно в терминах пространственной схемы взаимодействия объектов [29]. При этом на данном этапе был использован лишь верхний уровень – пространство функциональных преобразований P. Рассмотрение соответствующих подпространств функциональных расширений PP{F}{P} и более глубоких уровней вложенности связано с разложе- нием процессов внутренней неопределенности в зависимости от сложности задания или требуемого уровня когнитивных способностей. Подпространства характеристических расширений пространства функциональных преобразований PP{L}{P} формируются на основе факторов стимулирования процессов внутренней неопределенности для каждого уровня мышления. Реализация ступени синтеза фильтров состоит из четырех пронумерованных функциональных блоков, соединенных между собой ключом, который показывает переход от одного пространства к другому (точкой обозначается исходное пространство или подпространство) [29] (рис. 2). Функциональные блоки 1–4 представляют собой совокупность алгоритмов для решения поставленных задач для входной пары {D, f}, где D Î {L, G}, f Î {F, H} – композиции представлений цифрового фильтра в s-области и z-области соответственно. Обозначение y определяет некоторый функционал преобразования с параметрами α Î A, где A = {α > –1: α Î R}, и ϕ Î F, где F Î {G, X}, G = {g > 0: g Î R}, X = {x: x Î |z| < 1}. Опишем задачи для каждого блока. 1. Блок оценивания параметров фильтра y: D ´ ´ f ® f и обобщенного фильтра yα: (D, α) ´ f ® f: - задача построения модели фильтра в s-области; - задача построения модели фильтра в z-области; - задача оценивания коэффициентов фильтра в s-области; - задача оценивания коэффициентов фильтра в z-области. 2. Блок понижения эффективной размерности модели фильтра: - задача оптимизации полюсов фильтра yϕ: (D, ϕ) ´ f ® f; - задача понижения размерности фильтра yϕ: (D, ϕ) ´ f ® D. 3. Блок понижения эффективной размерности модели обобщенного фильтра: - задача оптимизации полюсов обобщенного фильтра y{ϕ,α}: (D, ϕ, α) ´ f ® f; - задача понижения размерности обобщенного фильтра y{ϕ,α}: (D, ϕ, α) ´ f ® D. 4. Блок стимулирования внутренней неопределенности yϕ: (D, ϕ) ´ f ® ϕ и y{ϕ,α}: (D, ϕ, α) ´ f ® ® (ϕ, α), который формирует пару выходных ключей {4, –}. Описанные функциональные блоки соединены ключами {1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}, по которым передаются входные и выходные параметры, требуемые для решения поставленных задач. Содержание выходных ключей более подробно рассматривается далее при описании метода повышения эффективности регрессионных моделей.
Роль входной пары в данной подсистеме играет {X, u}, где X – пространство признаков для описания тестируемых (обучаемых); u Î U – вектор ответов для заданного уровня мышления; модель поведения при тестировании h: X ´ u ® u. Приведем описание задач для каждого блока [30]. 5. Блок формирования тестовых заданий: - задача создания инструкций согласно форме тестирования (с множественным выбором) с необходимым количеством правильных и конкурентных неправильных ответов или дистракторов (distractors); - задача согласования инструкций с таксономией Блума в зависимости от уровня мышления обучаемого и сложности задания. 6. Блок формирования банка ответов: - задача сбора ответов обучаемых за тестовые задания; - задача выявления проблемных заданий, изменение формулировки и порядка представления заданий; - задача обработки событий, возникающих при тестировании, а именно: 1) количества и последовательности нажатий при выборе дистракторов; 2) индикатора активности окна с текущим заданием, возврата к окну с предыдущим заданием, перехода к окну со следующим; 3) отсутствия нажатия в случае пропуска задания; - задача контроля времени срабатывания событий в выделенный интервал тестирования. 7. Блок создания моделей индивидуального и группового поведения h: X ´ u ® u [31]: - задача расширения пространства признаков X и корректировки вектора ответов u на основе функциональных блоков 5 и 6; - задача проведения статистического анализа: 1) построение описательной статистики для контрольных групп и t-теста; 2) проверка адекватности и надежности заданий с α-Кронбаха; 3) проверка целостности и однородности ответов через выявление аномалий (чистых угадываний и мнений другого участника группового обучения), построение гистограмм и диаграмм размаха; - задача формулирования и доказательства гипотез (утверждений) для описания поведения обучаемых в условиях внутренней неопределенности; - задача создания концептуальных и математических моделей поведения на основе гипотез и утверждений. 8. Блок создания модели обучения при вероятностной трактовке параметра внутренней неопределенности c† Î [0, 1]: - задача оценивания уровня когнитивности hc†: X ´ (u, c†) ® u; - задача понижения размерности пространства признаков, описывающих поведение при индивидуальном и групповом обучении hc†: X ´ (u, c†) ® X. 9. Блок создания модели обучения при нечеткой трактовке параметра внутренней неопределенности cL† в условиях нечетко заданных когнитивных уровней и/или группового обучения: - задача оценивания уровня когнитивности hcL†: X ´ (u, cL†) ® u; - задача понижения размерности пространства признаков, описывающих поведение при индивидуальном и групповом обучении hcL†: X ´ (u, cL†) ® X. 10. Блок стимулирования внутренней неопределенности hc†: X ´ (u, c†) ® c† и hcL†: X ´ (u, cL†) ® ® cL†, который формирует пару выходных ключей {10, –}.
11. Блок усиления алгоритмов машинного обучения с учетом внутренней неопределенности: - задача классификации gc: (X, c) ´ (y, c) ® y, где c Î [0, 1] задает вероятностный характер внутренней неопределенности при переходе от сознания человека c† Î [0, 1] к сознанию машины; - задача классификации gcL: (X, cL) ´ (y, cL)®y, где cL Î [0, 1] задает нечеткий характер внутренней неопределенности при переходе от сознания человека cL† Î [0, 1] к сознанию машины; - задача понижения размерности пространства признаков gc: (X, c) ´ (y, c) ® X, где c Î [0, 1] задает вероятностный характер внутренней неопределенности; - задача понижения размерности пространства признаков gcL: (X, cL) ´ (y, cL) ® X, где cL Î Î [0, 1] задает нечеткий характер внутренней неопределенности. 12. Блок стимулирования внутренней неопределенности: - задача стимулирования процессов забывания и угадывания при вероятностной трактовке gc: (X, c) ´(y, c) ® c; - задача стимулирования процессов забывания и угадывания при нечеткой трактовке gcL: (X, cL) ´ (y, cL) ® cL. Блок стимулирования внутренней неопределенности при нечеткой трактовке учитывает не только уровень тестируемого (обучаемого), но и уровень сложности задания по таксономии Блума [32–34], меру влияния группового обучения, а также различные факторы стимулирования для достижения наилучшего результата. Как видно на рисунке 4, функциональный блок также формирует выходной ключ {12, –}. Метод повышения эффективности регрессионных моделей реализован в виде функционального блока 13, собирающего информацию с выходных ключей: {4, 13}, {10, 13}, {12, 13} (рис. 4). Основное назначение функционального блока – формирование вектора внутренней неопределенности для описания перехода от сознания человека к сознанию машины. С этой целью надсистема анализирует информацию с выходных ключей подсистем в виде моделей: 1) yϕ: (D, ϕ) ´ f ® ϕ; 2) y{ϕ,α}: (D, ϕ, α) ´ f ® (ϕ, α); 3) hc†: X ´ (u, c†) ® c†; 4) hcL†: X ´ (u, cL†) ® cL†; 5) gc: (X, c) ´ (y, c) ® c; 6) gcL: (X, cL) ´ (y, cL) ® cL, описывающих методы стимулирования вектора внутренней неопределенности {ϕ, (ϕ, α), c†, cL†, c, cL}, сформированного в задачах цифровой фильтрации, тестирования и машинного обучения. Перечислим задачи, решаемые в функциональном блоке 13. 13. Блок формирования вектора внутренней неопределенности: – задача нормирования вектора неопределенности {ϕ, (ϕ, α), c†, cL†, c, cL}; – задача создания метрик подобия: 1) (ϕ, α) ~ c†, (ϕ, α) ~ cL†, {c†, cL†} ~ ϕ, {c†, cL†} ~ ~ α; 2) (ϕ, α) ~ {c, cL}, {c, cL} ~ {c†, cL†}; 3) (ϕ, α) ~ l, {c†, cL†} ~ l, {c, cL} ~ l; – задача упаковки исходных данных {D, f}, {X, u}, {X, y} с целью группировки заданий для распре- деленных вычислений в блоках с выходными клю- чами, то есть 4, 10, 12. При этом метрики подобия группы 1 отражают степень схожести описания процессов внутренней неопределенности между параметрами технической среды (область цифровой фильтрации) и социальной (область психометрии). Метрики груп- пы 2 направлены на выявление схожести между интегральным параметром, описывающим социально-техническую среду (область машинного обучения), и каждой средой в отдельности. Наконец, метрики группы 3 рассматривают степень схожести введенных параметров с регуляризационными методами в рамках одной среды (технической, социальной или социально-технической). Выводы В работе предложен метод повышения интерпретируемости регрессионных моделей, который дополняет задачи регрессии и классификации в контексте задач синтеза фильтров из области цифровой фильтрации и тестирования из облас- ти психометрии. Данные области связаны едиными процессами внутренней неопределенности, позволяющими сформировать трехступенчатую модель развития мышления и соответствующий математический аппарат. С целью формализации предлагаемого метода в работе также приведены реализации ступени синтеза фильтров, ступени тестирования и интегральной ступени регрессии/классификации в рамках пространственной схемы взаимодействия объектов. Благодарности Автор выражает благодарность д.т.н., профессору С.А. Прохорову за ценные замечания и рекомендации, способствующие повышению качества представления результатов исследований. Работа выполнена при поддержке Министерства образования и науки РФ, грант № 074-U01. Литература 1. Воронцов К.В. Математические методы обучения по прецедентам (теория обучения машин). URL: http://www.machinelearning.ru/wiki/images/6/6d/Voron-ML-1.pdf (дата обращения: 30.05.2017). 2. Vapnik V.N. The nature of statistical learning theory. Springer India, 1998, 314 p. 3. Vapnik V.N. Statistical learning theory. Wiley-Interscience, 1998, 768 p. 4. Lipton Z.C. The mythos of model interpretability. URL: arxiv.org/abs/1606.03490 (дата обращения: 30.05.2017). 5. Agresti A. Foundations of linear and generalized linear models. Wiley Series in Probability and Statistics, 2015, 472 p. 6. Hastie T., Tibshirani R., Friedman J. The elements of statistical learning: Data mining, inference, and prediction. Springer Series in Statistics, 2013, 745 p. 7. Donnelly S., Verkuilen J. Empirical logit analysis is not logistic regression. Jour. of Memory and Language, 2017, no. 94, pp. 28–42. 8. Everitt B.S. The Cambridge dictionary of statistics. Cambridge, Cambridge Univ. Press, 2010, 480 p. 9. Groth-Marnat G., Wright A.J. Handbook of psychological assessment. Wiley, 2016, 768 p. 10. Lewis-Beck M.S., Bryman A., Liao T.F. The SAGE encyclopedia of social science research methods. SAGE Publ., 2003, 1528 p. 11. Kulikovskikh I.M., Prokhorov S.A. Modifications of log-likelihood to measure floor and ceiling effects // Информационные технологии и нанотехнологии (ИТНТ-2017): сб. тр. III Междунар. конф. 2017. С. 1849–1853 (на англ.). 12. King J.J., O’Canainn T. Optimum pole positions for Laguerre-function models. Electronics Letters, 1969, no. 5, pp. 601–602. 13. Prokhorov S.A., Kulikovskikh I.M. Unique condition for generalized Laguerre functions to solve pole position problem. Signal Processing, 2016, vol. 108, pp. 25–29. 14. Величковский Б.М. Когнитивная наука: Основы психологии познания. М.: Академия, 2006. Т. 1. 448 с. 15. Hegel G.W.F. Hegel’s science of logic. Prometheus Books, 1991, 844 p. 16. Andersson P. Adaptive forgetting in recursive identification through multiple models. Intern. Jour. of Control, 1985, no. 42, pp. 171–185. 17. Kulhavy R. Zarrop M.B. On a general concept of forgetting. Intern. Jour. of Control, 1993, no. 58, pp. 905–924. 18. Vahidi A., Stefanopoulou A., Peng H. Recursive least squares with forgetting for online estimation of vehicle mass and road grade: theory and experiments. Vehicle System Dynamics: Intern. Jour. of Vehicle Mechanics and Mobility, 2005, no. 43, pp. 31–55. 19. Alberini C.M., LeDoux J.E. Memory reconsolidation. Current Biology, 2013, no. 23, pp. R746–R750. 20. Alberini C.M. The role of reconsolidation and the dynamic process of long-term memory formation and storage. Front. Behav. Neurosci., 2011, no. 5, p. 12. 21. Elliott G., Isaac C.L., Muhlert N. Measuring forgetting: A critical review of accelerated long-term forgetting studies. Cortex, 2014, no. 54, pp. 16–32. 22. Chan J.C.K. When does retrieval induce forgetting and when does it induce facilitation? Implications for retrieval inhibition, testing effect, and text processing. Jour. of Memory and Language, 2009, no. 61, pp. 153–170. 23. Cowan N. What are the differences between long-term, short-term, and working memory? Prog. Brain Res, 2008, no. 169, pp. 323–338. 24. Lord F.M. Applications of item response theory to practical testing problems. Mahwah, NJ, Lawrence, Erlbaum Associates, Inc., 1980, 274 p. 25. van der Linden W.J. Forgetting, guessing, and mastery: The MacReady and Dayton models revisited and compared with a latent trait approach. Jour. of Educational Statistics, 1978, no. 3, pp. 305–317. 26. Ken Cor M., Sood G. Guessing and forgetting: A latent class model for measuring learning. Political Analysis, 2016, no. 24, pp. 226–242. 27. Schapire R.E., Valiant L. The strength of weak learnability. Machine Learning, 1990, no. 5, pp. 197–227. 28. Shalev-Shwartz S., Singer Y. On the equivalence of weak learnability and linear separability: New relaxations and efficient boosting algorithms. Machine Learning, 2010, no. 80, pp. 141–163. 29. Прохоров С.А., Куликовских И.М. Создание комплекса программ на основе пространственной схемы взаимодействия объектов // Программные продукты и системы. 2012. № 3. С. 5–8. 30. Куликовских И.М., Прохоров С.А., Сучкова С.А., Матыцин Е.В. Комплексная система коллаборативного обучения на основе нечетких моделей для описания поведения систем с частичным знанием // Изв. СНЦ РАН. 2016. T. 18. № 4. С. 760–765. 31. Kulikovskikh I.M., Prokhorov S.A., Suchkova S.A. Promoting collaborative learning through regulation of guessing in clickers. Computers in Human Behavior, 2017, vol. 75, pp. 81–91. 32. Prudencio R.B.C., Hernandez-Orallo J., Martinez-Uso A. Analysis of instance hardness in machine learning using item response theory. URL: http://users.dsic.upv.es/~flip/LMCE2015/ Papers/LMCE_2015_submission_1.pdf (дата обращения: 30.05.2017). 33. Smith R.M., Martinez T., Giraud-Carrier C. An instance level analysis of data complexity. Machine Learning, 2014, no. 95, pp. 225–256. 34. Rijmen F., Tuerlinckx F., De Boeck P., Kuppens P. A nonlinear mixed model framework for Item Response Theory. Psychological Methods, 2003, no. 8, pp. 185–205. References
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4355&lang= |
Статья в формате PDF Выпуск в формате PDF (29.80Мб) |
| Статья опубликована в выпуске журнала № 4 за 2017 год. [ на стр. 601-608 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Выделение областей интереса на основе классификации изолиний
- Моделирование поведения интеллектуальных агентов на основе методов машинного обучения в моделях конкуренции
- Применение машинного обучения для прогнозирования времени выполнения суперкомпьютерных заданий
- Адаптация модели нейронной сети LSTM для решения комплексной задачи распознавания образов
- Параллельные вычисления при реализации web-инструментария распознавания образов на основе методов прецедентов
Назад, к списку статей